基于模糊K-Means的MBD随机样本分类仿真

2023-09-20李静波顾园园

计算机仿真 2023年8期

李静波,顾园园

(长春工业大学人文信息学院,吉林长春 130102)

1 引言

随着计算机技术的飞速发展,互联网通信或云储存空间内留存的数据信息也在持续不断增多[1]。面对信息量过载、信息分类不明确的网络数据库,用户急切地需要一种有效的方法,以快速、准确地提取出简洁、精练且有价值的目标信息。因此,研究人员提出将海量大数据样本进行分类,减少用户对目标信息的检索时间,提高用户对目标信息的获取效率。

王忠震[2]等人通过噪声样本识别算法对样本集中整体数据完成去噪处理,并过滤噪声干扰强烈且无法识别的样本数据,再利用K邻近(KNN)聚类原理将去噪后的优化样本集划分成质量相同的样本子簇,考虑到样本子簇的类间不平衡性,需要利用AdaBoost算法合成样本子簇的簇心,该簇心具备类间特征属性,可以通过决策树分类器的训练,实现海量大数据随机样本的分类,但是该方法存在分类准确率低的问题。王凯亮[3]等人通过深度玻尔兹曼机(DBM)对先验数据库内随机数据进行采样,再利用极限学校机(ELM)网络对采集到的样本集进行训练,获取样本集内负荷曲线相关的优化特征,将优化特征投入到数据集分类模型中,实现海量大数据随机样本的分类。但是该方法存在分类召回率低的问题。董明刚[4]等人通过Bootstrap算法选取数据块中小类样本组成A类样本合集,再利用DWES算法选取数据块中大类样本组成B类样本合集,分别计算两合集内各数据的熵值大小以此构建样本特征合集,将样本特征合集投入基分类中,实现样本集内整体数据的分类,但是该方法存在分类耗时长的问题。

为了解决上述方法中存在的问题,提出基于模糊K-Means的海量大数据随机样本分类仿真的方法。

2 数据降维及样本特征提取

2.1 数据降维

数据降维[5]是指将冗余杂乱的海量高维数据根据点对点的映射原理改变成空间结构紧凑、处理更加便捷的低维数据,举例来说,在网络数据库检索目标信息时,数据库内原始样本所具备的权重向量较为复杂,这种由于样本权重向量复杂而导致用户对目标信息检索失败的问题,称为“维度灾难”,为了避免“维度灾难”干扰后续的样本特征提取工作,需要对数据库内原始样本进行降维处理。目前研究人员推出的降维方法包括线性辨别分析法、多维尺度分析法、主成分分析法和因子分析等,其中,常用于海量大数据随机样本分类的降维方法是因子分析法。

1)因子分析建模

设随机选取的样本集内数据总量为x,观测样本数据的光谱维度从而建立因子分析模型,因子分析模型的表达式如下

T(x)=δ+gH+r

(1)

2)求解因子载荷矩阵的维度频率

以光谱维度为基础获取的因子载荷矩阵无论是在维度平衡方面还是在数据光谱细节方面都表现出极高的稳定性,为下一步样本集内整体数据的降维做好充足准备。根据精度原理推导因子载荷矩阵的维度平衡向量,精度奠定原理的表达式如下

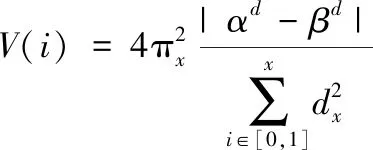
(2)

式中,π表示维度平衡常数;i∈[0,1]表示精度演算区间;dα-dβ表示邻近样本数据的权重差值。

根据协同方差计算公式获取因子载荷矩阵的数据光谱细节,协同方差计算公式的表达式如下

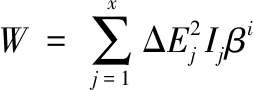
(3)

式中,β表示协方差系数;ΔE表示光谱突出的细节位点。

已知因子载荷矩阵的维度平衡向量和数据光谱细节,利用正交近似分解算法求解因子载荷矩阵的维度频率,正交近似分解算法的表达式如下

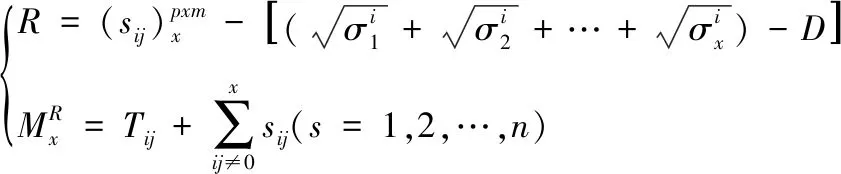
(4)

其中

(5)

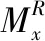
3)因子载荷矩阵的旋转

因子载荷矩阵的旋转建立在因子载荷矩阵维度频率求解成功的基础上,其目的在于旋转样本集中每个单位向量数据,使数据本身的维度频率尽可能靠近1或靠近0,以此实现样本集内整体数据的两极分离,进而突出每个单位向量数据与公共维度因子之间的关系,即单位向量数据的维度频率与公共维度因子的差值越大,说明该样本表现为高维正畸数据的概率越大,单位向量数据的维度频率与公共维度因子的差值越小,说明该样本表现为高维异常数据的概率越大。将两组数据归类,利用元素平方的相对差求和公式过滤高维异常数据,避免数据加权时,高维异常数据中心化对整体降维的影响。因子载荷矩阵的旋转过程依靠最大分量旋转法,旋转后的因子载荷矩阵表示为:

其中,ε表示矩阵旋转中心的因子参数;表示旋转角度。

元素平方的相对差求和公式如下

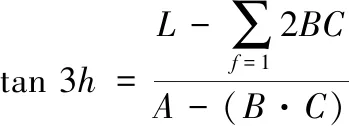
(6)

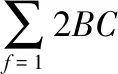
4)基于加权最小二乘法的样本集内数据降维

以优化后保留高维正畸数据的样本集为基础,利用加权最小二乘法对各数据进行降维,加权最小二乘法的表达式如下

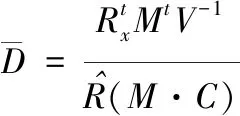
(7)

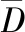
2.2 基于信息熵和相关度的低维数据特征提取

经过数据降维的样本集不仅降低了算法复杂度,还过滤掉了特征信息量较少且邻近特征信息冗余度过密的样本数据,使样本集内数据特征处于提取的最优阶段,基于信息熵[6]和相关度提取样本特征的操作步骤如下:首先利用wrapper方法计算样本集内各数据信息熵,规定信息熵阈值为c<1,若不满足阈值条件,则淘汰数据,反之,将满足阈值条件的数据整合为特征集,以特征集为基础,通过姿态特征选择算法检测内部数据相关性,若两数据相关性趋近于1,表示两者特征内容重合度高,需要利用异常检测算法[7]保留两者间特征信息量多的一方,并淘汰特征信息量少的一方。若两数据相关性趋近于0,表示两者特征内容重合度低,可以省略检测算法,同时保留双方数据。Wrapper方法的表达式如下

(8)

式中,Qm表示任意数据m的信息熵;∂表示wrapper系数。

姿态特征选择算法的表达式如下

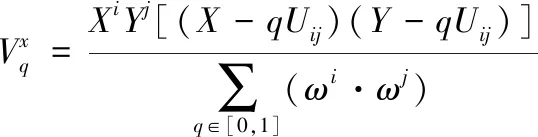
(9)

式中,XiYj表示数据i和数据j的相关性,当q趋近于1时,数据i和数据j的特征内容重合率满足ωi;当q趋近于0时,数据i和数据j的特征内容重合率满足ωj。

异常检测算法的表达式如下

(10)

其中

(11)

式中,B表示异常检测算法的准确率;n3表示异常检测算法的误检率。

经过信息熵阈值限定和相关度检测的样本数据在快速收敛函数[8]内完成多次迭代,实现样本特征的提取。快速收敛函数的表达式如下

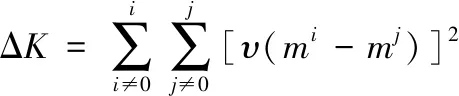
(12)

式中,υ表示快速收敛函数的常数;m表示迭代次数;ΔK表示样本特征矩阵。

3 基于模糊K-Means聚类算法的样本特征分类

模糊K-Means聚类算法是以样本特征为基础的一种簇族式分类方法,其具体操作为:首先利用初始聚类算法获取样本集内多个聚类中心[9],各样本特征值与聚类中心之间的距离被称为欧氏距离,视聚类中心为圆点中心,将欧氏距离不超过Lk的样本特征划分为一簇,以簇为单位,利用模糊K-Means聚类算法[10]获取各簇族的类别系数,根据最优聚类标准将类别系数相同的簇族进行归一化处理,得到基于模糊K-Means聚类算法的特征样本分类矩阵。模糊K-Means聚类算法流程如下图1所示。

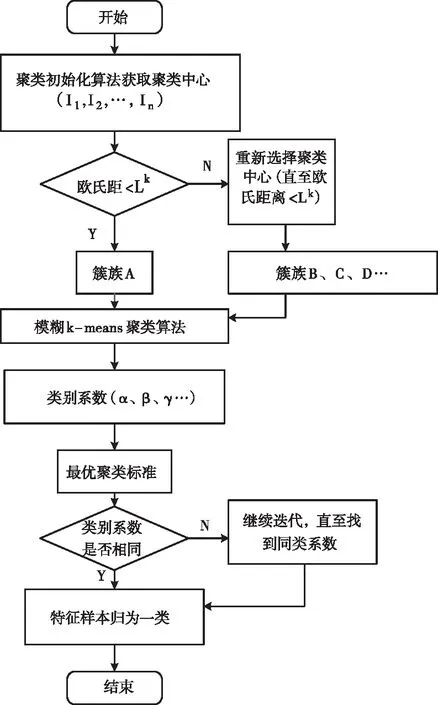
图1 模糊K-Means聚类算法流程

设待分类的样本特征集为k,且每个样本特征都与矩阵中的低维样本数据一一对应。将样本特征集输入初始聚类算法中获取该特征集的多个聚类中心[11]。初始聚类算法的表达式如下

(13)

式中,q表示初始聚类系数;k,l∈[0,1]表示聚类中心阈值;R(k·l)表示满足聚类中心限制条件的样本特征数[12,13]。

在成功获取样本特征集多个聚类中心后,观察各样本特征值与聚类中心之间的欧氏距离,完成样本特征簇族单位的划分,并以此为基础,加入模糊K-Means聚类算法获取各簇族的类别系数。模糊K-Means聚类算法的表达式如下

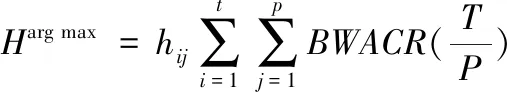
(14)

最优聚类标准的表达式如下

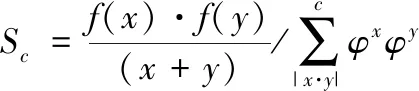
(15)

式中,f(x)表示最优聚类系数;f(y)表示类别系数归一化参数[14,15];Sc表示特征样本分类矩阵。根据特征样本分类矩阵实现海量大数据随机样本的分类。

4 实验与分析

为了验证基于模糊K-Means的海量大数据随机样本分类仿真的整体有效性,需要对其进行测试。

选择1000篇新闻稿件组成样本数据集A,稿件主题涉及时政、经济、娱乐、新媒体等30多个类别;选择3000篇语言类稿件组成样本数据集B,稿件语言涉及英文、俄文、日文等20多个类别;选择5000篇说明书类稿件组成样本数据集C,稿件内容涉及机械、计算机、工业机器等10多个类别,上述三组样本集内各数据信息的关键词、样本特征、类别属性均无序且混乱,分别采用不同方法对三组样本数据集进行分类,测试指标为准确率、召回率、F1值以及分类时间。准确率、召回率、F1值的计算式如下

(16)

式中,N表示样本数据的总数;accuracy表示准确率;recall表示召回率。

1)准确率

对比所提方法、文献[2]方法和文献[3]方法的分类准确率,进而评估不同方法的分类性能。不同方法的准确率对比如图2所示。

由图2可见,所提方法在三组样本数据集中的分类准确率均不低于95%,说明所提方法在面对任意样本数据集时均能表现出精确度较高的分类能力,这是因为所提方法利用因子分析法对样本数据集进行降维,从而得到运算简便的低维数据,低维数据的获取不仅提高了样本特征的分类准确度,还加快了样本数据集的分类速度,大大提升了用户获取目标信息的效率。文献[2]方法和文献[3]方法在三组样本数据集中的分类准确率分别不超过70%和50%,两者均与所提方法存在一定差距,说明文献[2]方法和文献[3]方法的分类精确度较低。经上述对比可知,所提方法的分类准确率高。

2)召回率

为了进一步验证不同方法的分类性能,对比提方法、文献[2]方法和文献[3]方法的召回率,对比结果如下图3所示。

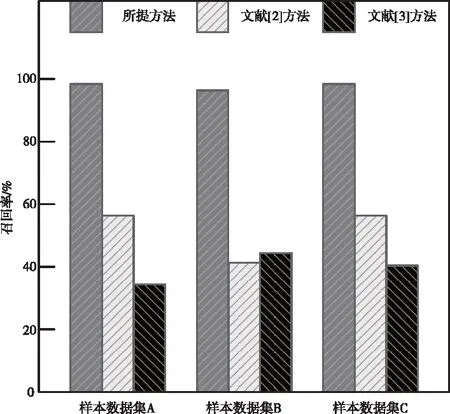
图3 不同方法的召回率对比

由上图3可见,所提方法在三组样本数据集中的召回率均接近100%,说明所提方法具备良好的分类能力和稳定性。文献[2]方法和文献[3]方法在三组样本数据集的召回率分别低于60%和50%,说明文献[2]方法和文献[3]方法的分类能力较差,与所提方法存在较大差距。经上述对比,进一步验证了所提方法的分类性能更强。

3)F1值

通过F1对精度和召回率进行整体评价,以突出所提方法的性能优势。不同方法的F1值对比如下图4所示。

图4 不同方法的F1值对比

由上图4可见,所提方法在三组样本数据集中的F1值均不低于90%,而文献[2]方法和文献[3]方法在三组样本数据集中的F1值分别低于75%和65%,可见所提方法在分类能力上明显优于传统方法。

4)分类时间

采用不同方法对样本数据集进行分类所消耗的时间与该方法的分类效率成反比,观察所提方法、文献[3]方法和文献[4]方法对三组样本数据集进行分类所消耗的时间,为避免统计学误差,同时计算三组样本数据集的平均分类时间。不同方法的分类时间对比如下表1所示。

表1 不同方法的分类时间对比

由上表1可知,所提方法在三组样本数据集中的分类时间及平均分类时间均低于1s,说明所提方法能够快速实现海量数据的分类,适用于发展迅速的大数据网络时代。文献[3]方法和文献[4]方法在三组样本数据集的分类时间及平均分类时间分别超过1.19s和2.26s,两者与所提方法存在一定差距。经上述对比可知,所提方法的分类耗时短,分类效率高。