基于NURBS和Slerp插补机器人S型速度规划

庞智慧,王桂荣,陈 晓

(1. 中国计量大学机电工程学院,浙江 杭州 311018;2. 浙江钱塘机器人及智能装备研究有限公司,浙江 杭州 310000)

1 引言

工业机器人的作业过程中,末端轨迹的柔顺性是评价机器人作业质量的重要指标之一[1]。实际工业生产过程中,欲使机器人按照规划路径运动,一般要经过轨迹规划、速度规划、插补三个阶段[2]。

机器人末端的轨迹规划包含对末端位置和姿态的规划。李永梅等[3]针对机器人的码垛作业,根据路径点要求,设计了多段直线的末端轨迹,保证精确通过各路径点,适用于对作业精度要求不很精确的情形;John[4]以抛物线过渡为例,运用直线+多项式曲线过渡的方式,在复杂曲线的关键路径点附近采用多项式曲线过渡,得到了较为光滑的末端轨迹,但此算法的复杂度随着中间点的增多而急剧上升。而且,上述算法主要针对末端姿态不变的情形,如末端姿态发生变化,要根据描述末端姿态的方式,选用对应的规划方式[5]。李黎等[6]基于RPY角描述末端姿态的方式,对三个角度分别进行规划,结合对位置变量,实现了末端位姿轨迹的规划。此方法适用于绝大多数姿态,但T. Teramae[7]指出,当绕任意轴旋转角接近0°或180°时调整绕固定轴旋转的相邻姿态会出现姿态的过渡不连续;Y. Nakamura[8]采用四元数描述旋转运动可有效避免上述问题,可以用来描述机器人末端的姿态。

上述对机器人末端进行轨迹规划时,解决了末端按照何种路径作业的问题;而速度规划解决了机器人经过规划路径的方式。J. R[9]对比了梯形速度规划和S型速度规划,指出梯形速度曲线由0加速到匀速vmax的过程中,会出现加速度的突变,作业过程会出现抖动,而S型速度曲线将作业过程的速度分为加加速、匀加速、减加速、匀速、减减速、匀减速、加减速7段,保证了加速度的连续性,有效避免了速度突变,进而改善作业质量。

本文针对六轴串联型机器人,对光滑性较好的NURBS曲线,运用S型速度规划方法,实现了末端轨迹的柔顺性,及作业过程中关节空间与笛卡尔空间下速度的平滑,确保加速度不会发生突变,保证了机器人作业过程的平稳性,减小机器人作业时的冲击与抖动。最后,通过仿真与实验,对本文算法进行验证。

2 机器人末端轨迹构造

对于机器人末端作业路径的规划,一般先确定作业过程中的关键点,通过插补构造末端路径。其中,以微小直线段连接相邻关键路径点的方式最为简单,但在两相邻线段的公共点处,会有方向的突变,整个作业过程也会有很多不光滑点,从而影响作业的质量。文献[3]的规划方法在构造复杂轨迹时捉襟见肘,文献[4]的规划方法在中间点过多时算法效率较低,且缺少对末端姿态的规划;而SHI[10]中提出的NURBS曲线可以根据一系列关键路径点作为控制顶点,并在不同的路径点处给定不同的权因子,构造出一种统一的曲线模型,同时,由于NURBS曲线具有可微性,满足机器人作业中对于末端轨迹的光滑性要求。此外,结合基于四元数描述的机器人末端姿态规划,可以满足复杂作业轨迹的要求。

2.1 NURBS曲线构造

一般而言,一条k次NURBS曲线表达式如下式(1)

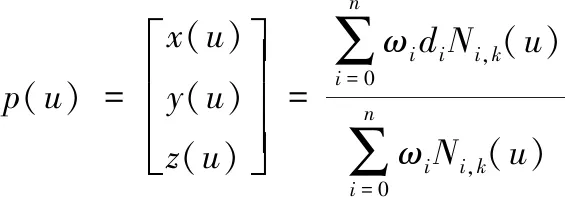
(1)

其中,di—n+1个控制顶点,i=0,1,…,n;ωi—n+1个控制顶点处的权因子,ω0>0,ωn>0,其它ωi≥0;u∈[0,1]—归一化因子;U=[u0,u1,…,un+k+1]—节点向量,各ui非递减;两端节点处重复度一般取为k+1,u0=u1=…=uk=0,un+1=un+2=…=un+k+1=1;中间各ui步长为1/(n+1-k),即uk+1=1/(n+1-k),uk+2=2/(n+1-k),…un=(n-k)/(n+1-k);Ni,k(u)—n+1个控制顶点处对应的k次B样条基函数,详见文献[10]。由式(1)可知,NURBS曲线可以表示为笛卡尔空间下各坐标分量的形式。

由文献[11]中所述,NURBS曲线的一阶、二阶导数公式如下

(2)

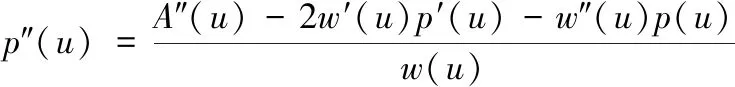
(3)

其中p(u)=A(u)/w(u);根据式(1)中NURBS曲线的分量形式,结合式(2)、式(3)中NURBS曲线的一阶、二阶导数公式,可求得各节点处三个分量方向的速度、加速度。

运用NURBS曲线进行插补[12]时,需要已知当前时刻的弧长才可进行速度规划。从p(u1)点到p(u2)点的NURBS曲线长度L为

(4)

一般而言,式(4)中的被积函数很难得到原函数,故选用文献[13]所述的Simpson数值积分的方法计算NURBS曲线长度,如下式(5)所示

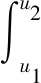
(5)

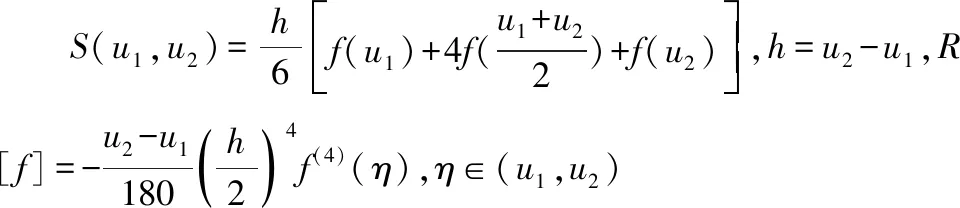
2.2 基于四元数描述的机器人末端姿态规划

由本文引言部分所述,基于四元数的机器人末端轨迹规划可以插值得到平滑的旋转,有效解决RPY角线性插值时三维旋转的不平滑问题。

单位四元数有两种描述形式

q=s+ai+bj+ck

(6)

(7)

式(7)中旋转轴为f=fxi+fyj+fzk;

联立式(6)、式(7),有

(8)

式(6)中所述四元数对应的姿态矩阵为

(9)

笛卡尔空间下绕单位向量f旋转θ角度,得到式(10)所述的旋转矩阵

(10)

其中,逆时针旋转为正,顺时针为负。显然,式(9)与式(10)等价。

联立式(9)、式(10),有

(11)

由式(11)可直接由机器人末端姿态矩阵求出对应的四元数。由于未规定旋转方向,故对应2个共轭的四元数。

对于由四元数描述的任意两组姿态q0和q1,一般有两种方法,Lerp和Slerp。Lerp即为线性插值,即

Lerp(q0,q1,h)=q0(1-h)+q1h

(12)

其中h可理解为NURBS曲线中的参数u,h∈[0,1]。

图1中,Lerp插值沿着单位圆圆弧上从q0到q1的弦上插值,因此Lerp插值出来的四元数不是单位四元数。将插值得到的四元数正规化,为Nlerp插值,即

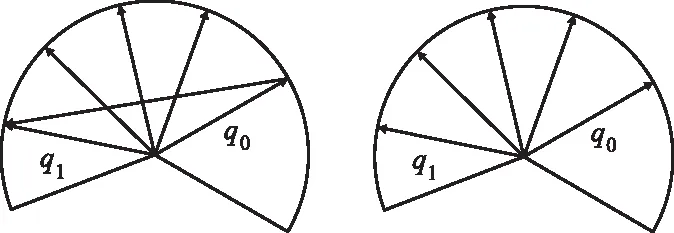
图1 Lerp插值&Slerp插值

(13)

上述插值方法中,当h在区间[0,1]内均匀分布时,得到的插补段并不是均匀分布的,即Lerp插值只具有形式上的“线性插值”。

Slerp(球面线性插值)是对角度的线性插值,即

θh=(1-h)θ0+hθ1

(14)

其中,θ0和θ1分别为四元数q0和q1的旋转角。令θ0=0,则θh=hθ1。由文献[7]可知,Slerp插值可以表述为

qh=Slerp(q0,q1,h)=αq0+βq1

(15)

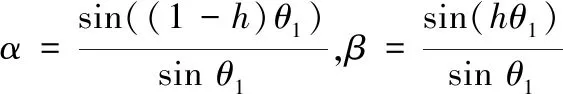
(16)

Slerp插值给出了四元数描述的球面上两点之间最短的插值曲线,且转角均匀变化。为了提高四元数对姿态的规划效率,避免姿态的冗余变化,选择q1与-q1中与q0夹角较小的做Slerp插值,即

Slerp(q0,q1,h)=

(17)

Slerp插值对h一阶、二阶导数分别为

(18)

(19)

(20)

3 机器人轨迹规划算法设计

本文设计的机器人轨迹规划算法如下:

1)构造末端轨迹

机器人的末端轨迹包含机器人末端的位置和姿态,合称为位姿,是作业过程时间t的函数;因此,可以对位置和姿态分别规划。由本文第一章所述,机器人末端位置采用NURBS曲线规划,姿态采用四元数的Slerp规划;

2)划分关键点

对Step1中构造出的机器人末端轨迹按照机器人的插补周期划分为n段,得到n+1个关键路径点;

3)对关键点处求逆解,逆解取优

工业机器人的工作空间分为关节空间和笛卡尔空间。关节空间下机器人通过运动学正解可得到一组关节角对应的末端位姿;反过来,笛卡尔空间下通过机器人的运动学逆解可求得对应的关节角,而且运动学逆解所得的关节角通常不唯一,需要进行逆解取优。

机器人正运动学方程为

(21)

式(21)也可表述为

x=x(θ)

(22)

式(22)两端对时间t求导,有

(23)

式(23)也可表述为

(24)

式(24)两端对时间t求导,有

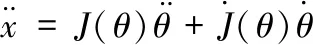
(25)

机器人的逆运动学求解,可以用KDL、IKFAST[15]等运动算法库。KDL采用Newton-Raphson迭代法[16]求解运动学逆解的数值解;IKFAST针对满足Pieper法则[17]的机器人,求解运动学逆解的解析解。机器人运动学逆解的求解速度直接影响了机器人轨迹规划的实时性,因此选用一种快速准确的运动算法库具有重要的意义。

机器人求解运动学逆解时,一般需要进行逆解取优。逆解取优原则通常为各关节的运动变化量最小,即运动姿态变化最平缓。此处可以参照笛卡尔空间下位移的定义,定义关节空间下的“位移”

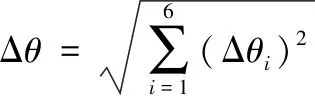
(26)

即式(26)中的Δθ最小,或Δθi最小。

4)在关节空间进行S型速度规划

S型速度规划可以保证加速度连续变化,有效减小了机器人作业过程中关节电机的冲击,避免作业过程中的频繁起停,因此可选用S型速度曲线在关节空间下对各关节角度进行规划。

七段式S型速度规划中,包含加加速、匀加速、减加速、匀速、减减速、匀减速、加减速7段加减速过程,如图2所示:

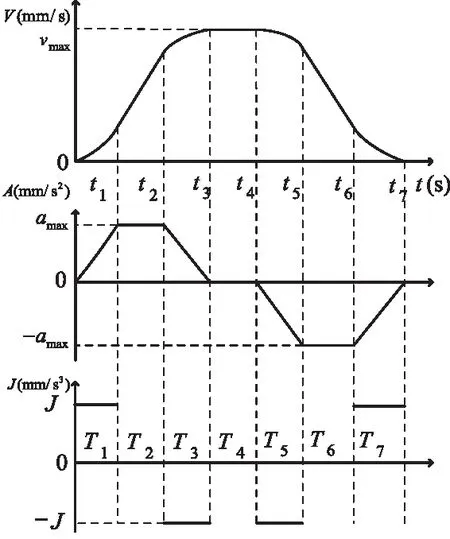
图2 七段式S型速度规划

图2中,每段结束时刻记为t1～t7,每段用时为T1～T7,位移为s,有

T1=T3=T5=T7,T2=T6

(27)

S型速度规划中,五段式缺少匀加速、匀减速段,即T2=T6=0;六段式缺少匀速段,即T4=0;四段式缺少匀加速、匀速、匀减速段,即T2=T4=T6=0。

S型速度规划流程图如图3所示。

图3 S型速度规划流程

图3中,s1、s2分别为经过加加速段、匀加速段、减加速段达到最大速度完成的位移,以及仅经过加加速段、减加速段达到最大速度完成的位移。

(28)

(29)

S型速度规划过程中,需要输入待规划段的起点终点的位姿坐标、输入最大速度vmax、最大加速度amax,以及各关节电机的加加速度J,计算s、s1、s2,根据图3中的规划流程,判断S型速度规划的类型,根据文献[14]计算S型速度规划过程中由本章(2)中n+1个关键路径点所得n段轨迹的时间、速度、位移;之后按照机器人插补周期得到n段轨迹内所有插补点的关节角,发送至各关节电机,按照本文所述的规划方式得出规划轨迹,与原有激励轨迹进行对比分析;

5)将4)中n段轨迹内规划所得所有插补点的关节角度、角速度、角加速度代入式(22)、式(23)、式(25)所述运动学正解、速度、加速度的表达式,得到笛卡尔空间下位姿的各个分量关于时间t的曲线,以及末端速度、加速度曲线。

机器人末端轨迹规划的流程图如图4所示。

图4 机器人末端轨迹规划流程图

4 仿真结果分析

4.1 机器人运动学模型

机器人正逆运动学的求解,需要先建立机器人的连杆坐标系,求解机器人的DH参数。本文采用SR4C机器人作为研究对象,其DH参数如表1所示:

表1 SR4C的DH参数

表1所示的DH参数表中,ai(mm)为连杆长度,αi为扭转角,di(mm)为连杆偏移量,θi为关节角。SR4C机器人各关节均为旋转关节,因此关节角可在限位范围内任意给定。

4.2 仿真结果分析

为了验证本文所述算法的有效性,选取机器人常用的伯努利双纽线作为激励轨迹,据此构造NURBS曲线。伯努利双纽线方程

(x2+y2)2=2a2(x2-y2)

(30)

(31)

取焦距a=50√2mm;激励轨迹如图5所示。

图5 激励轨迹

NURBS曲线参数:曲线次数k=3;节点向量U=[0,0,0,0,1/313,2/313,…,312/313,1,1,1,1];控制顶点由式(32)确定:

(32)

其中i=0,1,…,315;式(32)为伯努利双纽线的参数方程,其中θ取值范围[0,π/4],[3π/4,5π/4],[7π/4,2π],θi步长为0.01rad;控制因子为ω=[1,1,…,1];控制顶点个数n+1=316;所构造NURBS曲线是机器人末端按照伯努利双纽线作业时,在机器人基坐标系的坐标表示。

机器人末端姿态的规划采用本文2节所述的Slerp规划,即转角均匀变化。由式(21)中的机器人运动学方程可求出式(32)对应的位姿矩阵,结合式(11)即可求得对应的四元数。

本文中,由式(32)可以得到规划过程中的所有路径点,结合本文算法可构造出末端的激励轨迹,输入的速度、加速度、加加速度参数如表2所示:

表2 各关节参数

为了说明本文所提算法的有效性,选取基于5次多项式的S型速度规划的方式做对比,即式(32)中相邻路径点之间采用5次多项式构造激励轨迹,得到激励轨迹的对比图,如图6所示。

图6 本文算法与5次多项式

由图6可知,相比于5次多项式的规划方式,本文所提算法规划出的轨迹更加接近真实的激励轨迹,且轨迹的光滑性有显著的提升。采用本文算法与5次多项式规划的激励轨迹的曲率图如图7所示。

图7 不同规划算法的曲率图

其中,NURBS曲线上任意点曲率计算公式可由文献[11]确定。

(33)

由图7可知,采用5次多项式规划所得的激励轨迹只在有限个点处曲率值不为0,说明5次多项式规划的激励轨迹由多段直线组成,激励轨迹平滑性有待提高;而本文所提算法基于NURBS的曲线构造方法,整段激励轨迹上曲率均不为0,且曲率值低于原激励轨迹,即构造较为平缓的NURBS曲线,有效提高了激励轨迹的平滑性。

根据图4中的轨迹规划流程,可得本文算法规划所得的各关节位移、速度、加速度曲线,如图8所示。

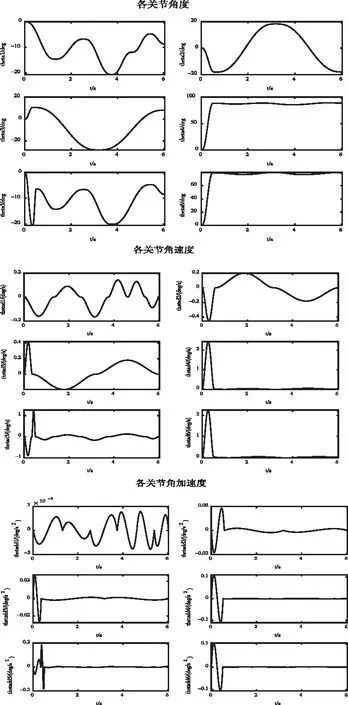
图8 本文规划下关节空间曲线

图8中,按照本文所提规划算法作业过程中,各关节的角加速度随时间连续变化,未出现突变现象,保证了角速度、角度曲线的光滑性,避免了5次多项式规划中出现的频繁起停的问题,减小了关节电机作业过程中的冲击,一定程度上延长了关节电机寿命;同时,随着关节电机角度曲线光滑性的提升,作业质量也随之改善。

5 小结

本文对工业机器人作业过程中末端轨迹的平滑性进行研究,基于NURBS曲线规划的方式构造一出种统一的曲线模型,改善了作业路径的平滑性;通过基于四元数的Slerp规划方法对末端姿态使机器人末端姿态均匀变化,减少了姿态冗余的情形;S型速度曲线使得速度曲线变得平滑,避免了5次多项式规划方式中机器人频繁起停的问题,各关节加速度不会产生突变,减小了作业过程中对关节电机的冲击,保证了作业质量,延长了各关节电机的使用寿命。