基于模型预测的无人车辆自主控制仿真研究

杨瑞雯,刘宇晨,张宇飞,曹博淳

(北京工业大学信息学部,北京 100124)

1 引言

随着人工智能技术和智能算法体系的不断发展,无人车辆自主行驶技术也得到了快速发展。现阶段,无人车辆的自主行驶技术已经可以实现一定程度上自动化的无人行驶,甚至在规则场景下可以在没有人为干预的情况完成整个自主行驶过程。

针对自由工况和复杂场景的无人车辆自主行驶技术仍是当前的研究热点。其中,速差转向车辆是一种典型的针对复杂环境行驶的车辆平台,在车辆行驶过程中速差转向平台依靠两侧驱动机构与行驶路面间的相互作用,产生速度差,实现期望的纵向与横向动作[1]。速差转向车辆无最小转向半径约束,可适应无规则的越野条件和更复杂的城市环境,拥有巨大的发展潜力,是进行综合环境无人车辆高精控制技术研发的理想平台[2]。

智能控制策略是无人车辆的核心驱动,无人车算法仿真系统是基于模型数字化的仿真系统,可以对无人车的控制算法进行测试、评估和优化,可以提高控制算法的开发效率、降低开发成本、提高算法开发安全性。

作为无人车辆的控制执行系统,无人车辆的路径跟踪控制能力是完成自动行驶任务的关键之一[3]。跟踪控制系统从车辆的局部路径规划子系统输入期望路径点,利用控制策略生成并执行控制命令,如车辆底层控制系统所需纵向行驶速度和横向横摆角速度等。经典的无人车辆控制策略有基于预瞄距离的纯跟踪(Pure Pursuit)控制算法,即根据一定的预测距离在拟合的期望路径上确定跟踪目标点,然后根据确定的目标点和无人车辆当前状态计算控制量[4]。在预瞄式多点路径控制策略中,跟踪误差是通过计算期望路径和预测路径来获得,计算过程中多目标约束被视为优化目标,基于IPEM的算法中利用横向和纵向速度的多项式函数来估计车辆位置,进行误差预测完成路径跟踪[5],但控制精度仍依赖车载定位系统和车辆模型的准确性。随着计算性能的提高,部分研究倾向于采用模型预测控制MPC的方法来实现无人车辆的控制策略,控制器可以同时处理多约束和多目标问题,为多个目标的集成优化提供联合解决方案,并且可以综合考虑不同系统的多个约束。文献[6]提出了一种基于随机 MPC的方法,用于处理线性化误差和模型不确定的控制系统,该方法利用反馈矩阵来完成轨迹控制[6],但未考虑模型误差带来的控制问题。文献[7]提出了一种基于运动学的速度估计方法,该方法通过收集驱动轮转速和车辆加速度信息进行了分析,完成了纵向和横向速度的估算,从而提高跟踪精度[7]。

本文提出了基于预测控制的无人车辆自主控制仿真方法,实现智能算法在仿真环境下的高效优化迭代。本文结构分为五部分:第一部分对现阶段无人车辆自主控制与轨迹跟踪做出概述,第二部分重点对无人车辆模型展开分析,第三部分对仿真控制器原理及设计过程进行论述,第四部分设计仿真试验并验证仿真控制器,第五部分对研究内容进行总结。

2 模型分析

当前无人车辆中常见的转向模式有阿克曼转向、速差转向和万向轮转向。其中,在阿克曼转向系统中,左右两轮轮轴的交点不在同一个位置上,而是略微偏离中心点,在车辆行驶过程中,左右轮分别跟随着自己的转向半径行驶,从而实现了内外轮转角的差异。当车辆需要进行大幅度转弯时,内侧轮的转向角度会比外侧轮更大,从而实现稳定的、精确的转向控制;万向轮转向是将多个小型的、可旋转的轮子固定在车辆底盘上,并通过特殊机构实现自由转动,从而实现车辆的转向功能。此两种转向模式车辆在行驶条件较好的城市路面或平坦路面有着良好的性能,但无法完全适应无规则越野环境和复杂城市环境。

在速差转向模式下,车辆行驶两侧机构的速度差对转向系统起到了决定作用。转向过程中,通过控制内、外两侧行驶速度差值实现车辆转向,速差转向车辆具备更加稳定的行驶特性,在特定环境中具有一定优势,作为本文所提仿真方法的研究对象。

2.1 模型定义

在理想速差转向车辆模型中,首先建立大地参考系G(X,Y,W)和车辆本身参考系L(x,y,ω)。设定无人车辆在二维平面运动,且车辆质心位于车辆几何中心。

如图1所示,为速差转向车辆在G和L坐标系下的运动学参数之间的关系,可以看到车辆整体在左右两侧驱动速度差之下完成转向,围绕转向中心oc进行刚体旋转,转向半径的大小取决于速度差值与纵向车速的大小。

图1 理想状态下速差转向模型

在此车辆运动学模型中,ol和or分别为驱动机构相对于大地坐标系G的旋转中心,且与无人车辆整体旋转中心在一条直线上,但此模型未考虑两侧驱动机构转向过程中相对于地面接触面的滑转和滑移运动,存在一定的模型误差。

为了更加准确的实现车辆控制仿真,缩小仿真系统与实车系统之间的模型误差。仿真系统中车辆模型采用基于滑动参数的运动模型,将速差转向车辆滑转和滑移特性量化处理,如图2所示。

图2 基于滑动参数的车辆模型

图3 仿真控制器设计流程

图4 无人车辆物理仿真模型

在此模型中,设定车辆状态变量x[vx,vy,vz],分别代表车辆纵向车速、横向车速以及转向角速度。

2.2 问题建模

(1)

subjectsm(x,u)=0

n(x,u)≤0

(2)

通过车辆转向过程的运动学关系,车辆状态参数x可以如式(3)表示。

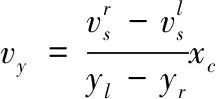
(3)

在大地坐标系G下,无人车辆非约束运动学差分方程可以表示为式(4)。

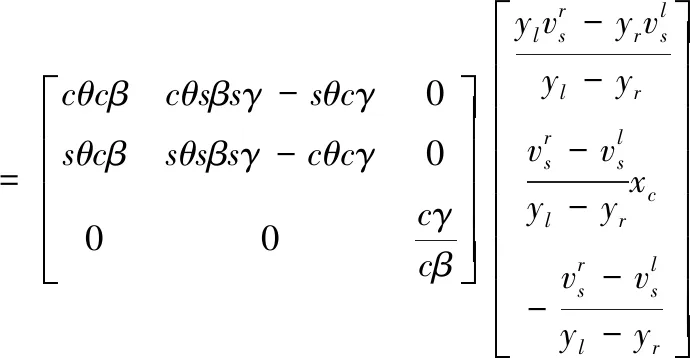
(4)

其中c和s分别表示cos和sin函数,γ,β,θ分别表示横滚角、侧翻角和航向角。

进一步车辆状态差分方程可以表示为式(5)所示:

(5)

3 控制器仿真

无人车辆智能控制器是由智能算法模块构成,驱动无人车辆完成特定自主任务。研究中针对无人车辆轨迹跟踪控制器设计开发仿真驱动。

基于优化理论的非线性求解器IPOPT应用于车辆状态方程(5)中,可以获得车辆当前状态x的离散差分方程如式(6)所示:

(6)

以模型预测控制算法为核心驱动,以离散差分方程为车辆状态转移规则,设计无人车辆控制模块,仿真控制器驱动流程如下图所示。

在整体仿真过程中,控制器仿真计算无人车辆控制序列,输出至无人车辆物理仿真模型,完成自主行驶任务。在控制器仿真中,以车辆当前状态和期望轨迹作为输入变量,优化过程中模型预测控制算法考虑车辆驱动约束、能量约束、优化代价约束、模型采样间隔和滚动时间窗口,计算最优控制序列。在无人车辆物理模型仿真中,根据控制器的期望控制指令完成左右两侧驱动机构动作指令的计算和执行。

在模型预测控制算法中,将式(1)具体化设计目标函数,其中cte[k]为横向误差、epsi[k]为航向误差、D[k]为转向约束、v[k]-vref为速度约束、D[k]-D[k-1]为转向变化量,v[k]-v[k-1]为速度变化量,向量P[Pi,i=1～6]为对应状态的权重系数,最终优化目标函数为式(7)。

v[k-1])2

(7)

控制向量u由横向控制量D和纵向控制量V构成,具体定义如式(8)所示。

(8)

4 仿真测试

4.1 测试环境

为了验证无人车辆自主控制仿真的准确性,在Vrep仿真环境下构建速差转向车辆物理仿真模型,并通过ROS操作系统完成控制器算法开发,实现物理仿真模型的驱动仿真。

其中,无人车辆物理模型由两侧驱动机构与中间车架构成,完成车辆自主行驶任务,驱动装置由车辆前端驱动轮带动履带转动与地面接触相互作用完成直线行驶与转向动作,仿真模型具体物理参数见表1。

表1 无人车辆仿真模型参数

4.2 结果分析

设计无人车辆控制系统仿真试验,验证仿真方法有效性。试验中,无人车辆分别以高速度7.5m/s和低速5m/s两个车速,进行车辆直线行驶及圆弧转向试验,验证仿真模型及仿真控制器的控制误差。

如图5所示,为无人车辆在车速V=5 m/s时的仿真测试,其中红色为期望跟随轨迹,而蓝色为仿真无人车在本文所提控制器下的行驶轨迹,可以发现车辆基本跟随期望轨迹,控制误差相对较小。

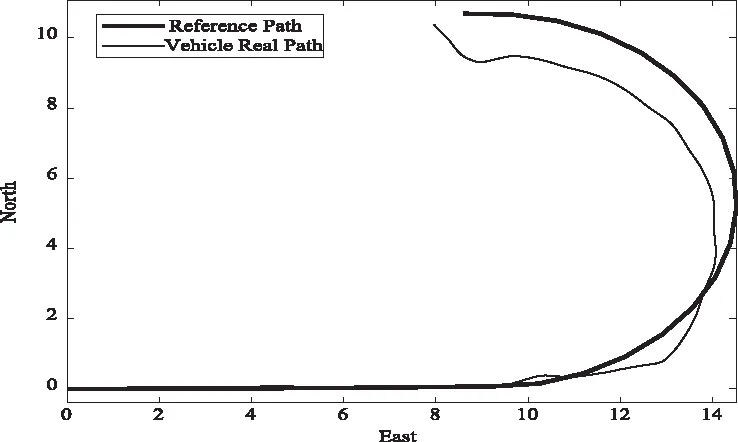
图5 速度5m/s时的仿真控制测试

如图6所示,为无人车辆在车速V=7.5 m/s时的仿真测试,此速度接近物理仿真车辆速度上限。其中红色为期望跟随轨迹,而蓝色为仿真无人车在本文所提控制器下的行驶轨迹,可以发现车辆直线行驶时基本跟随期望轨迹,控制误差相对较小,转向行驶时控制误差略大,但仍可跟随期望轨迹完成自主行驶任务。

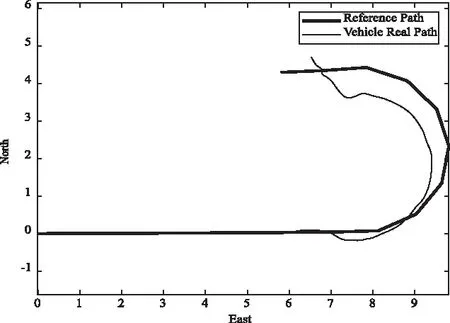
图6 速度7.5m/s时的仿真控制测试

5 结论

本文设计了速差转向车辆基于模型预测控制的仿真方法。首先,对速差转向车辆进行运动学建模,建模过程中将内外侧驱动机构的滑转和滑移因素进行量化考虑;其次,将无人车辆控制问题转化为多约束优化求解问题,利用非线性求解器IPOPT实现优化;然后,以两侧驱动机构控制量为输入,构建无人车辆物理仿真模型;最后,设计直线行驶与转向行驶的仿真试验,验证了所提仿真方法具备良好的无人车辆直线行驶仿真性能与较好的转向行驶仿真性能,提升了无人车辆系统智能控制算法的开发效率,对完善无人车辆仿真设计系统奠定了基础。