基于K近邻链式相似性度量的聚类算法
2023-09-20刘佳伟唐锦萍
刘佳伟, 唐锦萍
(黑龙江大学数据科学与技术学院,黑龙江 哈尔滨 150080)
1 引言
聚类算法作为一种重要的数据分析方法应用非常广泛,在图像处理[1,2],推荐系统[3,4],隐私保护[5,6]等方面也有着重要作用。聚类的目的在于将数据集中的样本划分为若干个,通常是不相交的子集,每个子集称为一个“簇”。使得簇内的样本同质性尽可能高,而不同簇样本之间的异质性尽可能高。
聚类算法中涉及一个基本的问题——相似性度量。通常基于某种形式的距离来定义“相似度度量”,距离越大则相似度越小,距离越小则越相似。
如果将聚类分为两个阶段:相似性度量阶段和划分阶段,传统的聚类算法中大多数采用欧式距离作为相似性度量。以K-means[7]为例,相似度量采用的是欧式距离,划分方法采用的是比较简单的划分为距离最近的聚类中心。自K-means之后有众多学者专家针对聚类过程中的划分方法做了很多改进:Nguyen[8]提出K-modes算法,将K-means使用的欧式距离替换成字符间的汉明距离,从而应用于非数值型的数据集上;K-medoids[9]针对K-means中聚类中心选择会受到极端值影响的问题,改为选择当前簇中其它点到该中心点的距离之和最小的样本点作为聚类中心,可以削弱异常值的影响;谱聚类[10]将聚类问题转化为图划分的问题,相比K-means,它能在任意形状的样本空间上聚类且收敛于全局最优解,并且适用于高维数据和稀疏数据;Bezdek[11]提出著名的FCM(Fuzzy C-Means)算 法,该方法是图像分割领域应用的较广泛的聚类算法;Martin Ester[12]等人提出一种代表性的基于密度的聚类算法——DBSCAN,该方法可以利用一个样本点ε领域内邻居点数衡量点所在空间的密度,该方法可以发现空间内任意形状的簇,也不需要事先知道聚类数目;STING[13]是一种基于网格的多分辨率聚类技术,它将空间区域划分为矩形单元。针对不同级别的分辨率,通常存在多个级别的矩形单元,这些单元形成了一个层次结构:高层的每个单元被划分为多个低一层的单元。Brendan J[14]等人于2007年提出Affinity Propagation(近邻传播)算法,该方法将全部的样本点当作潜在的聚类中心,数据点两两之间连线构成一个网络(相似度矩阵),再通过网络中各条边的消息(responsibility和availability)传递计算出各样本的聚类中心;Alex Rodriguez和Alessandro Laio[15]于2014年提出密度峰值聚类算法,该方法为了查找聚类中心,假设类簇中心点的密度大于周围邻居点的密度、类簇中心点与更高密度点之间的距离相对较大。
上述的这些方法,都是在聚类的划分过程中不断改进,但是相似性度量依然是基于欧式距离或者是其它传统的度量。在近些年,有部分学者关注到数据之间的非独立同分布的性质,针对数据间相似性度量做出改进并将其应用于聚类算法中,取得了不错的效果:Songlei Jian[16]等人认为样本的属性联系可以反映样本之间的非独立同分布性质,提出了CMS相似性度量方法,该方法从样本的属性出发计算样本之间的相似性,将其应用于谱聚类和K-modes聚类取得了良好的效果,但该方法复杂度过高;夏春梦[17]等人提出一种基于密度调整和流形距离的近邻传播算法,在近邻传播算法的基础上改进了距离度量,使用最短路径概念度量两个样本点之间的相似度;古凌岚[18]将密度和流形概念引入K-means算法中,利用K近邻来刻画样本点之间的相似性;温爱红[19]将将明可夫斯基和切比雪夫距离引入AP聚类中,取得了良好的聚类效果。
在改进相似性度量过程中,zhou[20]等人提出相似性度量要考虑数据的全局一致性和局部一致性,认为数据对象的相似性必须满足以下两个一致性条件:
1)局部一致性:如果两个数据点在空间位置上相邻, 这两个数据点很可能属于同一类。
2)全局一致性:若两个数据点处在同一流形,这两个数据点属于同一类的可能性比较大。
在传统的聚类算法中,大都采用了欧式距离或欧氏距离的简单转换作为样本间的相似性度量,这种方法在部分数据集中是可行,但是在一些具有特殊结构的数据集中则无法很好的反应样本点之间的全局一致性,下面以一个简单的例子说明。
如图1所示,在欧式距离的度量下,显然点a,c之间的距离Euclid(a,c)大于点a,b之间的距离Euclid(a,b),但是可以直观的从图中看出实际上a,c是属于同一簇而a,b分属于不同簇。由此可见,若根据欧式距离来进行后续的聚类过程,则会出现错误。针对这种情况本文提出一种新的距离度量,这种距离是在欧式距离的基础上通过构建近邻链来计算的,该方法在部分欧式距离无法适用的数据集上可以准确的反映数据间的全局一致性。基于改良距离度量的K-medoids[9],Affinity Propagation[14](AP)算法在仿真中取地了良好的聚类结果。

图1 欧式距离存在的问题
2 基于密度和近邻的链式距离
2.1 链式距离度量
从图1的例子出发,根据密度峰值聚类[15]中的理论,引入密度的定义:对于数据集中样本点i,i的密度为距离度量下与i距离小于ε的样本点的数目之和。其中ε为人为设定的阈值。在密度的基础上文献[15]提出了这样一种假设:
假设:在欧式距离度量下,数据集内同一簇样本点位于高密度区域,不同簇之间由低密度区域分割开来。其中高密度区域即该区域内的样本点的密度值较大。
在这样的假设下,基于欧式距离从数据集中任一样本点出发,检索距离其最近的一个样本点,当检索到的样本点与该点处于同一簇时,两样本之间的欧式距离会比较小,这是因为数据集内同一簇样本点位于高密度区域。再将检索到的样本点作为新的出发点,从未遍历过的点集合中检索下一个距离其最近的点,根据该方法逐个检索直到遍历完该簇所有点时,下一个点则会检索到距最后一个本簇点最近的一个异簇点,根据假设,此时这两个点之间的距离较大。根据这样的特性,考虑下面一种距离度量方法:从数据集中任一样本点出发,逐个搜索未遍历过的最近样本点直到遍历完数据集内所有样本点。根据此遍历结果将得到一条有序长链,将初始点到链上任一点的链式距离置为初始点到该点的子链中任一相邻两点的欧氏距离中最大值。由此可以得到初始点到数据集中任一样本点之间的链式距离。具体见如下定义:
定义1(最近邻链):设有数据集D,D中样本数量为n,di为数据集中任意一个样本点,下面定义中用Ci表示di的最近邻链,并记Ci(k)为该链上的第k个样本点,则Ci满足以下条件:
1)以di为初始点,即:Ci(1)=di.
2)Ci长度为n,且包含数据集D中全部的样本点。
3)链Ci上的第k个样本点,由下式确定
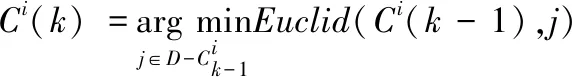
(1)

由式(1),Ci上的第k个样本点Ci(k)即是第k-1个点与未遍历过的样本点的欧氏距离的取得最小值时所对应的样本点
定义2(最近邻链式距离)设有数据集D,D中样本点di有最近邻链Ci,dj为Ci上一个样本点,且i≠j,则di到dj的链式距离
CD(i,j)=max(Euclid(Ci(q),Ci(q+1)))
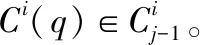
在理想状态下,应该遍历完一个簇再转移到另一个簇,这样同一簇点之间的链式距离小,而不同簇之间点的距离大,然而在实验中发现这样的方法存在一个严重问题即:一个簇未遍历完就会转移到另一个簇,以图2为例,存在下面这种问题:

图2 最近邻搜索存在的问题
问题 图2中有A,B两簇,假设选择a点出发,每一次寻找最近邻点,则会经过b,c,但是到d点时,下一步则会检索到距离点d最近的B簇的点e,这会导致A簇的已经遍历的样本点与A簇未遍历的样本点之间的链式距离发生错误。不能正确的反映数据的全局一致性。
针对这样的问题,参考在梯度下降法中陷入局部最优的问题的部分解决方法——扩大搜索步长、选择多起点搜索,采用了下面两种方法来解决:
方法1:在定义1中,最近邻链的定义通过检索距离当前点最近的点来得到的,考虑“扩大搜索步长”的方法:将检索最近邻点改为检索距离当前点最近的K个点,后从K个点中随机选择一个点作为下一次检索的起点。
方法2:在方法1的基础上,最近邻链式距离定义发生了改变,因为此时链式距离不再是稳定的。同时考虑引入“多起点检索”的方法:将a,b之间的最终的链式距离置为a到b的链式距离和b到a之间中的较小的那个,这样可以进一步缓解问题。同时将链式距离矩阵转化为对称矩阵。
在提出的方法1和方法2的基础上,基于K近邻的方法将最近邻链的定义改进为K近邻链,并得到最终的K近邻链式距离的定义:
定义3(K近邻链):设有数据集D,D中样本数量为n,di为数据集中任意一个样本点,下面定义中用CKi表示di的K近邻链,并记CKi(k)为该链上的第k个样本点,则CKi满足以下条件:
1)以di为初始点,即:CKi(1)=di.
2)CKi长度为n,且包含数据集D中全部的样本点。
3)记NK(CKi(k-1))表示欧式距离中K近邻意义下CKi(k-1)的K个近邻点的集合
其中K-argmin表示使得欧式距离最小的K个样本点。
4)在3)给出的K近邻点集的基础上,CKi(k)服从NK(CKi(k-1))中K个点的均匀分布,即
其中j∈NK(CKi(k-1)),因此可以同等的概率随机的选取K近邻点集中某一个点作为CKi(k)。
定义4(K近邻链式距离):设有数据集D,D中样本点di有K近邻链CKi,dj为CKi上一个样本点,且i≠j,则di到dj的K近邻链式距离为
CKd(i,j)=max(Euclid(CKi(q),CKi(q+1)))

CKD(i,j)=min(CKd(i,j),CKd(j,i))
2.2 全局性距离变换
在链式计算链式距离度量之前采用了指数函数来对欧式距离进行变换。
Euclid′(x,y)=γEuclid(x,y)-1
其中γ>1为放大系数。
根据指数函数的性质,在(0
2.3 链式距离计算
根据2.1和2.2节的论述,总结计算链式距离的完整过程如下:
输入:数据集D,D的欧式距离矩阵 Euclid-based Matrix(EM),参数K
输出:数据集的链式距离矩阵 Chained-based Matrix(CM)
1)利用式EM′(x,y)=γEM(x,y)-1对欧式距离矩阵做变换。
2)选择数据集中第一个样本点d1作为start point(sp)并记录。
3)在EM′中,寻找K近邻意义下sp的K个未记录过的近邻点的集合,在该点集中随机选择一个点作为next point(np)。
当未记录点数不足K个时,则在未记录点中随机选择一个作为np。
4)记录当前np,将当前np点作为新sp,重复步骤3)直至数据集中所有样本点均被记录,则得到一条以d1为起点遍历所有样本点的长链即d1的K近邻链CK1。
5)根据K近邻链式距离定义根据计算d1到D中任意一点dj的K近邻链式距离CKd(1,j)
6)依次选择数据集中所有点作为sp,重复步骤3)、5),计算得到数据集D中任意两点之间的链式距离。
7)通过
CKD(i,j)=min(CKd(i,j),CKd(j,i))
计算得到D的链式距离矩阵CM
2.4 复杂度分析
当数据集共有n个样本点时,链式计算距离度量需要分别从每个样本点出发根据一定规则寻找到一条长链。
当每次寻找下一个点为当前点的K近邻点集中的随机一个点时,复杂度为O(n),那么寻找一条链的复杂度为O(n2), 则寻找n条链的复杂度为O(n3)。
3 基于链式距离的聚类算法
3.1 链式距离与已有聚类算法的结合
在使用链式距离改进了聚类算法中的相似性度量后,下一步需要根据相似性度量来划分数据集。现有的聚类算法中提出了各种各样的划分方法,但是并不是所有划分方法都可以应用于链式距离上来对数据进行聚类,这是由链式距离的计算特性决定的。
以K-means为例,在K-means算法的聚类过程中,每一轮迭代,都将选取每一簇的样本点均值作为新的聚类簇中心,然后根据样本点到聚类中心的距离来划分该样本点的类别。显然,这样选取的聚类中心大多数情况下都不在给定的样本点中,因此,每一轮划分,都需要重新计算聚类中心到其它所有样本点的距离。
当使用传统距离时,聚类中心和其它点的距离可以直接计算,若用链式距离替换传统欧式距离,那么计算聚类中心到其它样本点的链式距离的过程将十分耗时,算法复杂度大大增加。
所以,考虑链式距离与划分方法的结合时,应优先选择基于距离矩阵,或者聚类中心仍然属于样本之一的聚类方法,比如K-medoids算法、Affinity Propagation算法、谱聚类方法。
3.2 K-medoids和Affinity propagation算法
在后续的实验部分,本文选择链式距离分别与K-medoids和Affinity propagation算法结合,一是因为这两种方法都是基于距离矩阵对数据集进行划分的,可以充分利用链式距离矩阵;二是因为这两种方法对于具有明显流形结构的数据聚类效果不理想。下面简述K-medoids算法和Affinity propagation算法的原理。
3.2.1 基于链式距离的K-medoids方法
K-medoids聚类是在K-means聚类基础上的改进。它们都对聚类中心进行迭代,区别在于K-means算法中,各个簇的聚类中心的计算采用的是簇内所有点的质心,也就是簇内各个样本点的平均值,由此所计算出来的聚类中心可以是连续空间中的任意值,而非已存在的样本点。与此不同,K-medoids算法中每一轮迭代的聚类中心一定是数据集中的样本点。
在后续的K-medoids聚类实验中,将算法中的欧式距离矩阵替换为链式距离矩阵后,算法的基本流程如下:
1)在样本点中随机选择K个聚类中心
2)根据链式距离矩阵计算各个样本点到聚类中心的距离
3)将每个样本点划分到距离其最近的聚类中心,形成K个簇C1…CK。
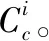

则
5)重复步骤2),3),直到满足迭代次数或误差小于指定的值。
3.2.2 基于链式距离的Affinity Propagation方法
Affinity Propagation(AP)聚类是一种基于图论的聚类, 它根据样本点之间的相似度进行聚类,这些相似度构成了所有样本点的相似度矩阵S,一般情况下相似度采用负的欧式距离表示。
AP聚类不需要人为指定簇的数目,它将所有样本点视为潜在的聚类中心,根据S主对角线上的值s(i,i)来判断样本点i是否可以成为聚类中心,该值越大,i成为聚类中心的可能越大,该值称为p值。若所有样本的p值相同,则所有样本成为聚类中心的可能性相等,样本的p值影响聚类得到的簇的数目,p值越大得到的簇越多,如果选择输入相似度矩阵的均值作为p的值则得到的簇的数目中等。
在样本点构成的网络中传递两种类型的消息(responsiility和availability)。r(i,k)表示k是否适合做点i的聚类中心,a(i,k)则表示i是否选择k作为其聚类中心。r(i,k)与a(i,k)的和越大,表示k作为聚类中心的可能性就越大。所有样本点的r(i,k)与a(i,k)构成了吸引度矩阵R和归属度矩阵A。为了控制收敛速度,算法还设置有阻尼因子(damping factor),用λ表示。AP 算法通过迭代不断更新每一个点的吸引度和归属度值,直到收敛或达到最大迭代次数心,然后将样本点分配到相应的聚类中心。
在后续的AP聚类实验中,本文采用负的链式距离来表示样本点的相似度矩阵S,聚类算法基本流程如下:
1)计算负的链式相似度矩阵S,设置参考度p、初始化吸引度矩阵R和归属度矩阵A。
2)根据下面公式更新吸引度矩阵R,其中
3)根据下面公式更新归属度矩阵A
at+1(i,k)
4)根据下式利用阻尼因子λ对矩阵R和A进行修正
5)重复步骤2),3),4)直到收敛或达到最大迭代次数。然后通过下式将样本点i划分到对应的聚类中心ci
ci=arg maxk(r(i,k)+a(i,k)).
4 实验
为了证明本文所提出的链式距离的有效性,分别在人工数据集和UCI数据集下做了对比实验。
在八个二维和三维人工数据集下分别计算欧式距离,切比雪夫距离,曼哈顿距离,最短路径距离[17]和链式距离,对比在不同距离度量下组内距离和组间距离的差异。将这五种距离度量结合K-medoids聚类和Affinity Propagation聚类算法,采用FMI(Fowlkes-Mallows Index)评分作为评价标准对比在八个人工数据集上的聚类性能。
在UCI 数据集中,选择了四个聚类算法-DBSCAN,Affinity propagation,K-medoids和Agglomerative层次聚类,分别在欧式距离和链式距离下通过这四种算法进行聚类,采用FMI评分作为评价标准对比不同算法在UCI数据集上的聚类表现。
4.1 数据集和算法参数设置
4.1.1 数据集
表1和表2分别列出了人工数据集和UCI数据集的基本信息,包括样本点数目,特征维数和聚类数目。图3、图4和图5为人工数据集中四个数据集的散点图,其中两个为二维数据集,两个为三维数据集,可以看到样本点的分布具有明显的流形结构。

表1 人工数据集基本信息

表2 UCI数据集基本信息

图3 三维数据集swiss_roll

图4 三维数据集two_hemisphere

图5 二维数据集two_moons、smile
4.1.2 参数设置
最短路径距离参数:放大系数γ=e。
链式距离参数:放大系数γ=e,K=e。
K-medoids算法:给定正确的聚类数目,初始聚类中心随机选择,每次计算迭代300次,取10次计算结果的FMI的均值作为最终结果。
Affinity Propagation算法参数:选择较小步长在一定范围内逐次选择不同的参考度p和阻尼因子λ,选择最佳聚类结果作为最终结果。
Agglomerative层次聚类算法参数:给定正确的聚类数目,判断两簇距离的方式的参数linkage选择average。
DBSCAN算法参数:选择较小步长在一定范围内逐次选择不同的ε-邻域距离阈值eps和判断样本点是核心对象所需的ε-邻域的样本数阈值min_samples,选择最佳聚类结果作为最终结果。
FMI评分:FMI是对聚类结果和真实值计算得到的召回率和精确率,进行几何平均的结果,取的值范围为 [0,1],越接近1越好。具体的计算方法如下
其中TP是真正例(True Positive),即真实标签和预测标签属于相同簇类的样本对个数;FP是假正例(False Positive),即真实标签属于同一簇类,相应的预测标签不属于该簇类的样本对个数;FN是假负例(False Negative),即预测标签属于同一簇类,相应的真实标签不属于该簇类的样本对个数。
4.2 人工数据集实验
4.2.1 距离矩阵对比
表3列出了不同距离度量下中簇间距离均值和簇内距离均值的比值,表4和表5分别列出簇内和簇间距离的方差。需要说明的是,为方便计算对比,本文只比对了8个数据集中6个2分类和3分类数据集。

表3 组间/组内距离均值的比

表4 组内距离方差均值
可以看到,与其它几种距离度量相比,链式距离度量在这几个数据集中尤其是具有环状结构的数据集two_circles和smile中,明显扩大了组间和组内距离的差异,并且降低了组间、组内距离的方差,更好的反映出数据集的全局一致性。
4.2.2 聚类结果对比
表6和表7分别列出了K-medoids算法和AP聚类算法的FMI评分,可以看出,不论是在K-medoids聚类还是AP聚类中,相比于其它四种距离度量,基于链式距离的聚类均取得了更优的结果,这也符合4.1节中对于距离矩阵的对比结果,说明链式距离在这种具有明显非凸特性的数据集上相比传统的距离度量可以更好的反映样本点之间的全局一致性。

表6 K-medoids聚类FMI

表7 AP聚类FMI
4.3 UCI数据集实验
表8分别列出了4个UCI数据集下,4种聚类算法分别基于欧氏距离和链式距离聚类的FMI评分,为了区别起见,基于欧式距离的算法使用E标识,使用链式距离的算法使用C标识,比如E-DBSCAN表示基于欧式距离的DBSCAN算法,C-DBSCAN表示基于链式距离的DBSCAN算法,其它依次。可以看到在Iris数据集中,使用欧式距离的聚类算法得到的结果均要优于使用链式距离的,而在其它三个数据集中,使用链式距离得到的聚类结果持平或者小幅优于基于欧式距离得到的聚类结果。

表8 基于欧氏距离和链式距离聚类FMI
通过这几组对比实验可以看到,链式距离和欧式距离在没有明显非凸特性的数据集上,对于数据集的全局一致性的反映程度接近。但链式距离的计算复杂度高于计算欧氏距离,并且链式距离鲁棒性较差,容易受到噪声影响。
5 结论
在本文中,从K-means方法存在的缺陷出发,针对欧式距离在非凸数据集中不能很好反应全局一致性的问题上,提出一种基于欧式距离的链式计算的新型距离度量。在具有明显非凸特性的人工数据集中,在传统K-medoids聚类,AP聚类中使用本文所提出的距离度量方法得到了明显优于传统距离度量的聚类效果。但是在没有明显非凸特性的UCI数据集中该方法相比欧式距离并没有明显优势。另外也显示了该方法存在以下几个缺陷:①该方法容易受到噪声的影响②该方法的复杂度较高。接下来的研究工作是进一步优化算法以减少距离矩阵的计算时间,以及针对具有不明显凸特性的一般数据集提升算法的聚类效果。
