基于改进乌鸦搜索算法的极限学习机分类方法
2023-09-20霍闪闪王章权
霍闪闪,苏 兵,王章权,孙 萍
(1. 常州大学计算机与人工智能学院,江苏 常州 213164;2. 浙江树人大学信息科技学院,浙江 杭州 310015)
1 引言
经过几十年的发展,神经网络理论在人工智能等研究领域取得了广泛的成功。其中,极限学习机(Extreme Learning Machine,ELM)[1]因其良好的插值能力[2]、通用逼近能力[3]和分类能力[4]而被广泛地应用于疾病诊断、交通标志识别、图像质量评估等多个领域。不同于传统神经网络,ELM在训练前只需设置隐含层神经元个数,通过随机生成连接输入层和隐含层之间的输入权重和隐含层神经元阈值,求解Moore-Penrose广义逆运算就能得到最优输出权重,极大地提高了算法的收敛速度[5]。但是ELM随机生成输入权重和阈值的方法导致部分隐含层神经元的作用很小,从训练样本中提取的信息不足以概括和反映数据的内在规律从而出现欠拟合问题,为解决欠拟合问题需要采用更多的隐含层神经元个数[6],在降低响应速度的同时增加了计算复杂度和内存消耗[7],因此需要对ELM输入权重和阈值两个参数进行优化改进[8],以实现网络模型优化。
目前常用群智能优化算法[9]、增量法和剪枝法去优化ELM模型,但增量法和剪枝法针对如何设计合适隐含层神经元个数选取准则、阈值选取准则等没有固定规律可循,导致得到的ELM模型不够稀疏,因此所提算法采用群智能优化算法去改进ELM模型。
针对ELM参数优化问题,Zhao等人[10]利用改进布谷鸟搜索算法对ELM中的输入权重和隐含层阈值进行优化,并对一些预测问题进行了研究,取得了较为理想的预测结果。Zhang等人[11]利用人工蜂群算法优化ELM的隐含层神经元个数。Zhu等人[12]利用混沌搜索策略鲸鱼优化算法优化ELM的隐含层神经元个数。上述论文均利用群智能优化算法对ELM隐含层的神经元参数进行寻优,减少了隐含层冗余神经元,提高模型稳定性,但同时引入了大量需要被优化的超参数,增加了算法的计算复杂度[13],削弱了ELM训练速度快的优势。
2016年伊朗学者Askarzadeh提出的乌鸦搜索算法(Crow Search Algorithm,CSA)[14]在全局搜索性能方面优于其它优化算法,并且CSA与GA、PSO等优化算法相比,只需要设置飞行长度(flight length,fl)和感知概率(Awareness Probability,AP)两个参数,相对消耗更少的计算时间,具有灵活性强、精度高且易于实现等优点[15],适合于ELM模型优化[16]。标准CSA算法通过位置迭代更新来获得乌鸦个体最优藏食位置,达到模型参数寻优的目的。为了保证具有较好寻优性能,要求在位置迭代更新前期,算法具有较好的全局搜索性能,避免陷入局部最优;在位置迭代更新后期,算法具有较好局部搜索性能,提高收敛速度。Shi等人[17]通过引入自适应惯性权重,在算法前期使用较大惯性权重增强全局搜索性能,在后期减小惯性权重避免过度搜索,提高收敛性能。Khalilpourazari 等人[18]引入正弦余弦局部优化算子,在全局遵循最优解优先规则,避免陷入局部最优,并设定特定的乌鸦移动方式,在局部提高收敛性能。上述算法通过引入额外的参数来优化模型的全局和局部搜索性能,但均使用固定AP值的选择搜索机制,而AP值直接影响搜索机制搜索性能(AP值较大,模型趋向全局搜索;AP值较小,模型趋向局部搜索),基于固定AP值的搜索方法难以满足CSA位置迭代更新的要求。
综上,本文提出一种基于改进乌鸦搜索算法的极限学习机分类算法:提出基于参数动态递变的优化乌鸦位置迭代更新方法,设计AP值动态递变函数,使得AP值在迭代前期保持较大值,保证算法可以趋向全局搜索,而随迭代过程逐渐减小,保证算法在迭代后期可以趋向局部搜索;并在全局搜索过程中,提出采用莱维飞行搜索方法替换传统的随机位置搜索方法,避免了盲目搜索,提高收敛速度,并在局部搜索过程中,提出采用多个体变因子加权学习方法,使用多个体学习方法代替传统的单个体学习方法,增强了种群多样性,提高局部极值逃逸能力。提出一种基于邻代维度交叉的最优个体更新方法,通过综合历代最优解维度信息实现较好分量的最大化保留,通过计算适应度值实现最优迭代位置更新,相比仅考虑相邻两代信息实现最优迭代位置更新的方法,提高了最优个体藏食位置质量,增强算法寻优性能。
2 基于改进乌鸦搜索算法的极限学习机
2.1 极限学习机模型
作为一种求解单隐含层神经网络训练框架[19],ELM网络结构与单隐层前馈神经网络(Single Layer Feedforward Neural Network,SLFN)一样,只是在训练阶段不再采用基于梯度下降的算法(后向传播),而是随机生成输入权重和阈值,采用Moore-Penrose(MP)广义逆矩阵理论计算输出权重。理论研究表明,ELM随机生成输入权重和隐含层阈值的方法,使其具有极快学习速度的同时仍保持SLFN的通用逼近能力。ELM网络结构如图1所示。
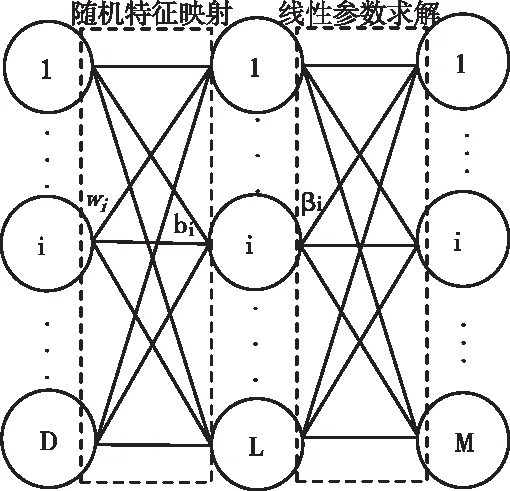
图1 ELM网络结构图
训练ELM模型时,设定训练集为{Xi,ti|Xi∈RD,ti∈Rm,i=1,2,…,N}(Xi表示第i个样本,ti表示第i个样本对应的标记,N为输入样本数量,D、L、M分别为神经网络输入层、隐含层和输出层的节点数量,wi为连接输入层与隐含层之间的输入权重,bi为隐含层阈值,βi为连接隐含层与输出层之间的输出权重。ELM训练分为两个阶段:随机特征映射和线性参数求解:
1)随机特征映射:随机生成输入权重wi和阈值bi,采用非线性映射激活函数将输入数据映射到隐含层,获得隐含层输出矩阵H,计算公式为
H(x)=[h1(x),h2(x),…,hL(x)]
(1)
hi(x)=g(wix+bi),wi∈RD,bi∈R
(2)
其中H(x)=[h1(x),h2(x),…,hL(x)]是经由上述非线性映射获得的隐含层输出矩阵,hi(x)是第i个隐含层节点的输出,g(·)是非线性激活函数,一般使用Sigmoid函数,Sigmoid函数映射图像如图2所示

图2 Sigmoid函数曲线图
g(x)=(1+exp(-(wTx+b)))-1
(3)
2)线性参数求解:“广义”的单隐含层前馈神经网络ELM的输出fL(x)是:
其中T为目标输出矩阵。

(4)
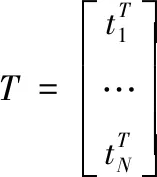
(5)
采用Moore-Penrose(MP)广义逆矩阵方法可以推导出输出权重β的值为

(6)
其中H†为输出矩阵H的逆矩阵。
2.2 基于改进乌鸦搜索算法的极限学习机
基于改进乌鸦搜索算法的极限学习机(ICSA-ELM)用改进乌鸦搜索算法(ICSA)对ELM的输入权重w和阈值b进行寻优,通过将w和b作为ICSA算法的藏食位置实现参数的最佳取值。主要内容包括:基于参数动态递变的优化乌鸦位置迭代更新方法和基于邻代维度交叉的最优个体更新方法,前者通过保持全局和局部搜索性能的平衡,避免局部极值,提高收敛速度;后者通过综合历代维度信息改善最优个体质量,增强算法寻优性能。
2.2.1 基于参数动态递变的优化乌鸦位置迭代更新方法
首先设计AP值动态递变函数,满足ICSA位置迭代更新的要求;在全局搜索过程中,采用莱维飞行搜索方法,提高收敛速度;在局部搜索过程中,采用多个体变因子加权学习方法,增强了种群多样性,增强局部最优值逃逸能力。
1)AP值动态递变函数
为了满足CSA位置迭代更新的要求,需要动态调整感知概率AP值,使其满足凸型递减曲线形状,构造基于迭代次数动态递变的AP函数,数学表达为
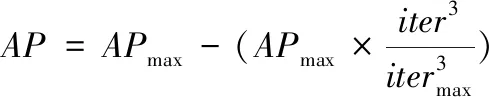
(7)
其中iter为迭代次数。
2)莱维飞行搜索方法
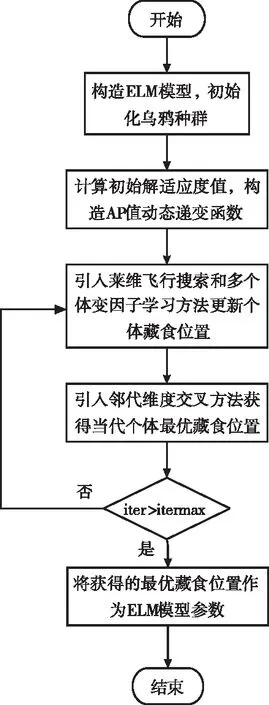
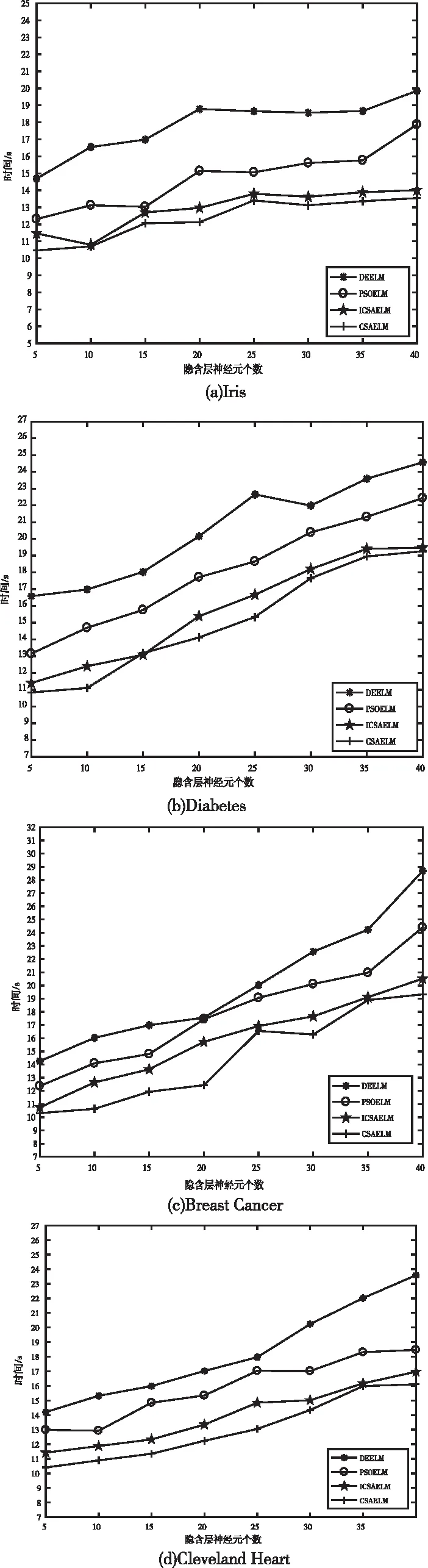
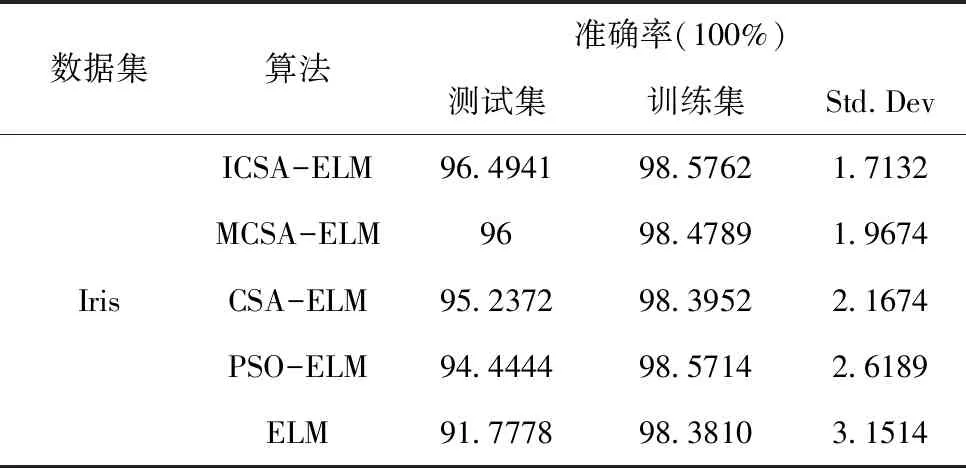
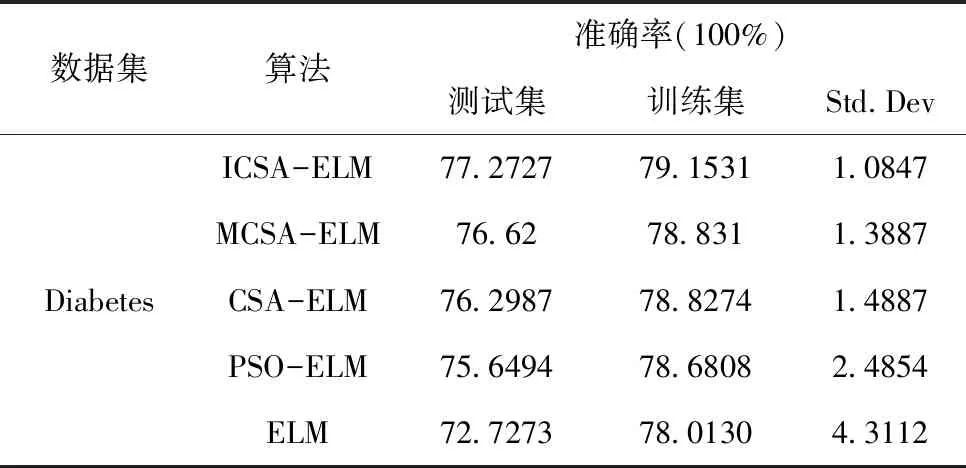
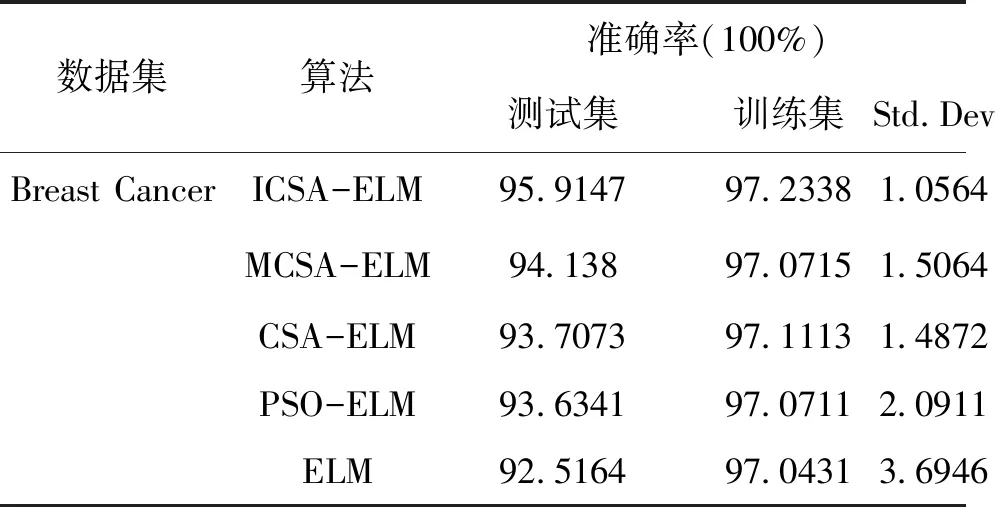
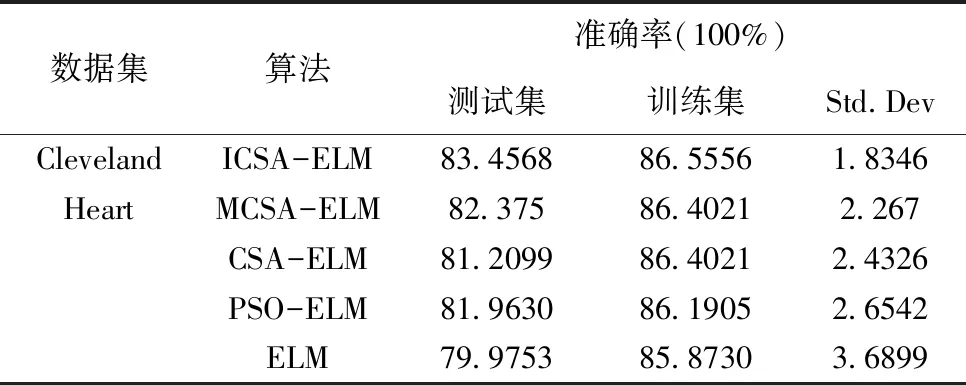
在位置迭代更新过程中,当乌鸦j感知到被乌鸦i跟踪时(即在r (8) (9) 其中α为步长缩放因子,控制乌鸦i搜索范围;rα为区间(0,1)区间内的随机数;γ、σ服从标准正态分布;Γ(x)=(x-1)!;s为取值范围在[1, 2]之间的常数,xi,iter+1为乌鸦i在第iter+1次迭代下的个体最优藏食位置。 3)多个体变因子加权学习方法 在位置迭代更新过程中,当乌鸦j未感知到被乌鸦i跟踪时(即在r>AP状态下),乌鸦i会跟随乌鸦j飞行,即执行局部搜索。采用多个体变因子加权学习方法,确保子代乌鸦可以同时向多个乌鸦个体学习,提高种群多样性,避免陷入局部最优,相应数学表达为 xi,iter+1=xi,iter+ri(1,d)×fli,iter× (λitermj,iter+(1-λiter)biter-1-xi,iter),rj≥APj,iter (10) λ=λmax-(iter×(λmax-λmin)/itermax) (11) 其中ri(1,d)是区间[0,1]之间的d维随机变量,λiter为第iter次迭代时的加权学习因子,biter-1为第iter-1代种群的最佳藏食位置,rj为乌鸦j在区间(0,1)之间的随机数。 2.1.2 基于邻代维度交叉的个体最优藏食位置更新方法 在位置迭代更新过程中得到的当代个体藏食位置由于受到部分变量影响,导致表现出较差适应度值无法进行更新替代,引入邻代维度交叉方法,通过综合历代最优解的不同维度信息,提高最优个体藏食位置质量,增强算法寻优性能,相应的数学表达为 (12) h=1,2,…,⎣Rcross×d」 (13) ICSA-ELM算法的具体流程如下,流程图如图3所示: 图3 ICSA-ELM算法流程图 步骤1:构建ELM模型,定义ICSA算法和ELM模型相关参数。随机初始化N个初始解(乌鸦的位置),生成的初始解维数为L×(n+1),第一个维数为L×n,表示输入权重,剩下的L维表示隐含层阈值。 步骤2:利用步骤1得到的解在训练数据集上训练ELM模型,计算每个解的适应度值和最佳位置,根据递变规则构造AP值动态递变函数,迭代更新ICSA参数。 步骤3:种群中所有乌鸦个体随机选择不同乌鸦跟随,采用莱维飞行搜索方法和多个体变因子加权学习方法,在跟随乌鸦的同时利用感知到的父代最优藏食位置生成自身藏食位置,并计算当前种群适应度值,检查新位置可行性,获得当前迭代最优解。 步骤4:采用邻代维度交叉方法计算并排序解之间的维度差异,保留历代最优维度,获得最优个体位置。 步骤5:判断算法是否达到最大迭代次数,如果满足,将获得的个体最优藏食位置作为ELM模型的输入权重和阈值去训练ELM模型;否则,返回步骤3继续运行算法。 为了减小随机性带来的影响,在每次验证ICSA-ELM性能实验中对所有测试进行50次,以提高算法稳健性。 种群进化最大迭代次数itermax设置为50,种群规模nPop设置为20,飞行长度fl为2,最大感知概率APmax为0.5, 加权学习因子λ递变区间为[0.05,0.95],维度交叉比例Rcross为0.3,步长缩放因子α为0.01,常数s为1.5,隐含层神经元个数范围设置为[5,40],步长为5。选取训练集数据分类精度、测试集数据分类精度和标准差作为ICSA-ELM性能评估标准,评估指标均采用平均值进行计算评估。 为验证文中所提ICSA算法性能,选取基准测试函数中的F8、F10两个测试函数进行验证测试,并与标准CSA算法结果进行对比分析,实验结果如图4所示。由实验结果可知,在相同约束条件下,在单峰测试函数寻优过程中ICSA算法具有更好的收敛速度和局部极值逃逸能力。 图4 平均迭代对比寻优 为验证文中所提ICSA-ELM算法性能,选择UCI机器学习数据库中的Iris、Diabetes、Breast Cancer和Cleveland Heart四个数据集进行测试验证。算法性能分析包括收敛性分析和分类测试结果分析。 4.3.1 收敛性分析 选取常用的优化算法(PSO,DE,CSA)对ELM进行优化,在四个数据集上计算不同隐含层数目下的ELM模型收敛时间,结果如图5所示。由实验结果可知,随着隐含层神经元个数的增加,ELM网络模型结构越复杂,计算复杂度越高,收敛时间越长。通过收敛时间对比可以发现,提出的ICSA算法与DE算法相比,在相同条件下收敛速度平均提高了5.5秒时间;与PSO优化算法相比,收敛速度平均提高了2.5秒时间;与传统CSA算法相比,收敛速度与其相差平均为1.5秒,有时甚至可以忽略不计。实验结果表明ICSA-ELM在进行分类操作时具有较好的收敛速度,一定程度上提升了算法效率。 图5 收敛速度对比分析 图6 不同数据集在不同隐含层神经元个数条件下的分类精度 4.3.2 分类测试结果分析 选取常用的优化算法(PSO、CSA、MCSA)对不同隐含层数目的ELM进行优化,在四个数据集上进行分类测试。表1、表2、表3、表4显示了在隐含层神经元个数为20的分类测试结果。实验结果表明,无论在训练集上还是测试集上ICSA-ELM算法的分类精度和标准差都是最好的,具有较好的泛化性能和稳定性。ICSA-ELM算法与MCSA-ELM算法相比,分类精度平均提高了1.1%,标准差平均减小了34%;ICSA-ELM算法与CSA-ELM算法相比,分类精度平均提高了1.8%,标准差平均减小了34%;与PSO-ELM算法相比,分类精度平均提高了2.3%,标准差平均减小了57%;与ELM算法相比,分类精度平均提高了4.5%,标准差平均减小了77%。 表1 Iris数据集测试结果的比较 表2 Diabetes数据集测试结果的比较 表3 Breast Cancer数据集测试结果的比较 表4 Cleveland Heart数据集测试结果的比较 图5显示了不同隐含层神经元个数下的分类测试结果,实验结果表明,随着隐含层个数的增加,算法分类精度会有一定程度的提高,但是当增加到一定程度时,分类精度会有所降低或基本保持不变。ICSA-ELM算法与其它算法相比,分类精度波动最小,具有更好的稳定性。 本文分析了ELM模型性能和相关缺陷,通过ICSA寻优搜索出ELM模型最佳输入权重和阈值,解决ELM随机生成隐含层参数带来的欠拟合问题。ICSA算法通过在算法迭代前期引入AP值动态递变函数平衡全局和局部搜索性能,在位置更新过程中引入莱维飞行搜索和多个体变因子加权学习避免盲目搜索,提高种群多样性,在最优位置选择过程中引入邻代维度交叉方法提高藏食位置质量,实现ELM模型最佳参数选取,从而提高模型分类精度。为评估算法性能,在UCI经典分类数据集上进行实验验证,实验结果表明该算法具有更好的分类效果和泛化性能。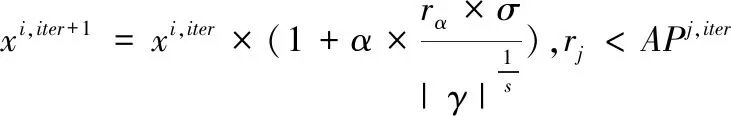
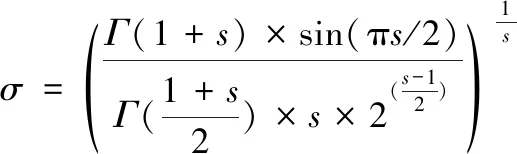


3 ICSA-ELM算法实现
4 算法仿真与分析
4.1 算法仿真环境
4.2 ICSA算法性能分析

4.3 ICSA-ELM算法性能分析

5 结论
