基于预报误差法的边界热流反演方法研究

王首彬,莘嘉庆,周 远

(1. 天津城建大学控制与机械工程学院,天津 300384;2. 哈尔滨工业大学仪器科学与工程学院,黑龙江 哈尔滨 150001)

1 引言

热传导反问题一直以来是一个跨学科难题,其计算推导的病态性、传热系统的阻尼性和延迟性等因素导致热传导反问题求解难度较大[1]。在工程实践中,边界条件、材料特性和未知热源等难以获得,需要通过温度测量和反问题算法来获取这些未知条件和参数的具体信息。

近年来,学者们针对常规最小二乘类优化方法的改进一直在进行,得到了一些较好的结果。文献[1]提出了带复杂变量的径向积分边界元法和LM算法相结合的方法,来辨识传热学反问题中的导热系数。Agarwal等[2]开发了估计模盐界面热通量的新方法,对比计算机辅助冷却曲线分析更加准确。文献[3]中提出了一种通过瞬态温度测量在线估算具有复杂几何形状的非线性导热系统的时变表面热流的新方法。文献[4]使用带有Tikhonov正则化的输出最小二乘法和改进的共轭梯度法估计了热通量等参数。

将最大似然函数法引入反问题的研究,能够提高不确定系统反演过程的鲁棒性和准确性。华盛顿大学Emery等联合莫斯科航空学院空间系统工程系[5]一起通过扩展的最大似然原理来处理已知模型参数中不确定性问题的逆解,并进行最佳实验设计,所得结果证明了整个方法的可靠和准确。美国康奈尔大学的王敬波等[6]提出了一种贝叶斯推理方法,该方法可以计算获得边界热通量的后验概率密度函数(PPDF),且反演结果准确性较好。本课题组针对热传导反问题,通过利用分散模糊推理法[7]、预测模型法[8]和顺序函数法[9]等进行研究,取得了较好的结果。

本文将预报误差原理应用到传热系统中,此方法不仅具有贝叶斯推理以及最大似然法的统计性质,而且无需确定观测变量的联合概率密度函数,即可辨识整个时间域中的边界热流,且所求结果具有良好的鲁棒性与准确性。

2 传热学正问题

如图1所示,二维非稳态传热模型Ω为数值实验对象,测点为S1、S2…Sd,排成一列,模型控制方程为(1)到(6)。图中加粗右边界为热流边界。

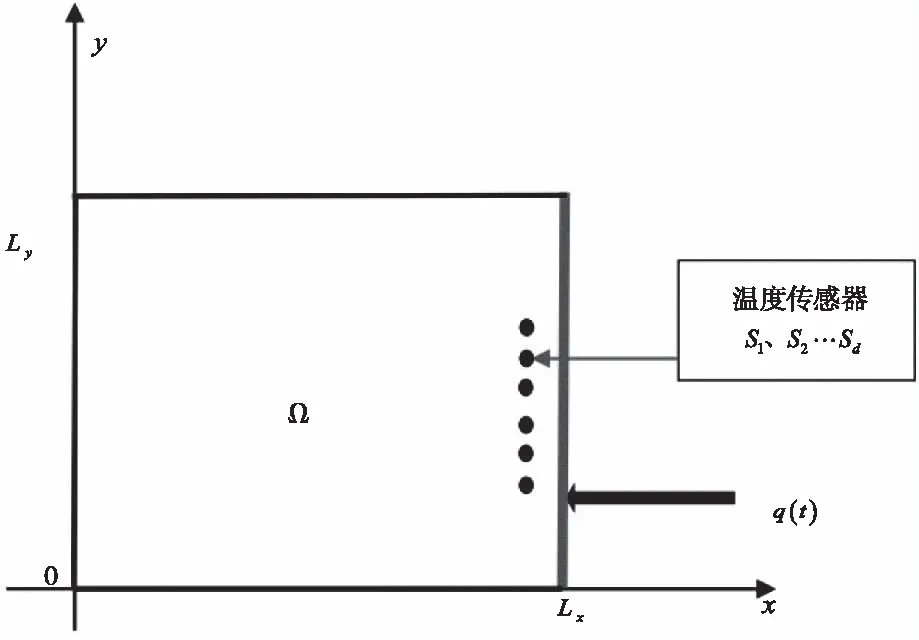
图1 二维非稳态传热模型

二维非稳态传热系统控制方程以及定解条件如下

(0≤x≤Lx,0≤y≤Ly,t≥0)

(1)

T(x,y,0)=T0,0≤y≤Ly,0≤x≤Lx

(2)

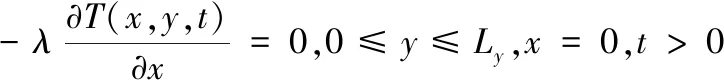
(3)

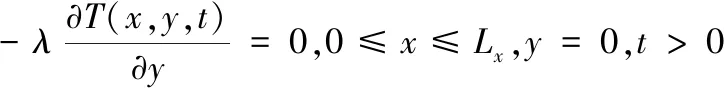
(4)

(5)

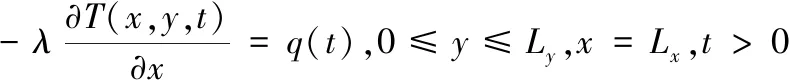
(6)

边界热流为q(t), 初始温度是T0,热扩散系数为α=(λ/ρc),λ是模型的导热系数,利用有限差分法[10,11]来求解传热正问题。

3 预报误差模型的建立及求解

针对传热反问题的不适定性和延迟性,引入顺序函数法的原理;预报误差法一般用于控制系统,因此根据传热系统的性质引入阶跃响应的概念。由重构的温度场、单位阶跃响应系数和顺序函数法原理共同构成预报误差公式,并通过求解相应的准则函数的最小值得到边界热流值。

3.1 传热系统的单位阶跃响应系数

单位阶跃响应函数定义为h(x,y,τk)=∂T(x,y,τk)/∂q(τk)其中τk为时间离散点k处的时间。h(x,y,τk)反映热流条件∂q(τk)作用下∂T(x,y,τk)的改变程度。式(7)中利用后一时刻τk的h(x,y,τk)与前一时刻τk-1的h(x,y,τk-1)做差所求得的Δh(x,y,τk-τk-1)就是从τk到τk-1时刻的单位阶跃响应系数。以此可类推得到不同时间段、不同测点处的单位阶跃响应系数,如式(7)到式(9)所示,其中,r为未来时间步数,k为离散时间点(k=1,…,H),H为离散时间点数,x,y分别为横纵坐标位置。

Δh(x,y,τk-τk-1)=h(x,y,τk)-h(x,y,τk-1)

(7)

Δh(x,y,τk+1-τk-1)=h(x,y,τk+1)-h(x,y,τk)

(8)

⋮

Δh(x,y,τk+r-1-τk-1)=h(x,y,τk+r-1)-h(x,y,τk-1)

(9)

以上设立的传热系统模型中,边界热流值是未知的,温度场受边界热流的影响而不断变化,因此可以将传热系统视为一个由边界热流为输入,温度场为输出的系统。据此提出单位阶跃响应系数:热流值增加一个单位,温度场的温度相应改变一个数值,即Δh(x,y,τk-τk-1)。简化公式令Δh(x,y,τi-τk-1)=Δh(d,m)。式中m=i-(k-1),(i=k,k+1,…,k+r-1)。

3.2 确立预报误差模型求解反问题

根据传热系统的特点,应用顺序函数思想中由未来时刻的输出值来预测当下时刻的输出值,具体过程如下:

已知正问题模型中前k-1个时间点的热流值q1,q2,…,qk-1和之后r个时间点内测点上的温度测量值Tk,Tk+1,…,Tk+r-1,同时假定时间τk,τk+1,…,τk+r-1的热流变化满足式(10)

qk=qk+1=…=qk+r-1

(10)

根据传热系统的阶跃响应系数、顺序函数原理和预报误差法原理建立预报误差模型如下

T(d,τm,qk)=T(d,τk,0)+Δh(d,m)*qk

(11)

式中T(d,τm,qk)是τm时刻d测点的测量温度,T(d,τk,0)是τk时刻d测点且假设当qk=0所重构的计算温度。Δh(d,m)是测点d处对应时刻的阶跃响应系数。根据顺序函数原理,假设qk为全部相同的辨识参数。

(12)

σ是通过以下公式获得的温度测量误差的标准差

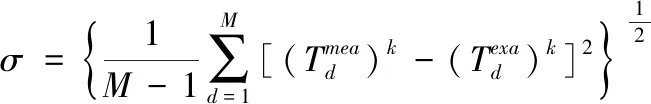
(13)

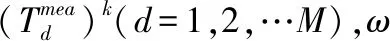
根据在反演热流值计算求得的重构温度值T(d,τk,0)和阶跃响应系数值Δh(d,m)的条件下,“最佳”的预报温度T(d,τm,qk)期望为

(d,τm,qk)=E[T(d,τm,qk)|T(d,τk,0),Δh(d,m)]

(14)

可以写作

E{‖T(d,τm,qk)-(d,τm,qk)‖2|T(d,τk,0),Δh(d,m)}

=min

(15)

显然这里的“最佳”温度预测就是模型的最佳输出。通过极小化预报误差准则式子(16),就可以获得“最佳”的热通量值:

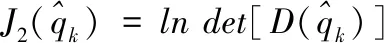
(16)

其中

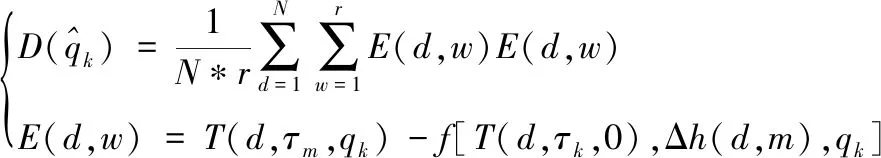
(17)

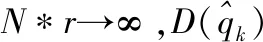
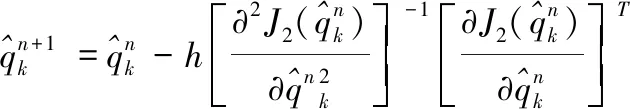
(18)

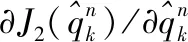
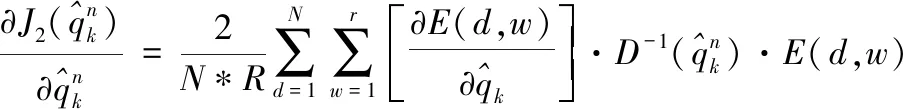
(19)

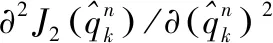
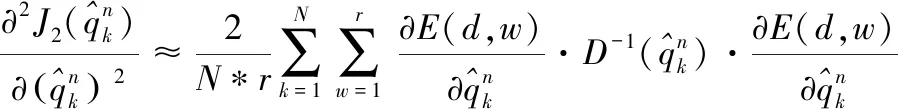
(20)

公式中

(21)

为了使得到的二阶导数正定,同时减少计算量,实际中常使用公式(20)作为近似二阶导数。

3.3 反问题求解流程

使用Newton-Raphson 法求边界热流的计算步骤如下:

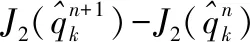
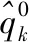
4 数值实验及讨论

4.1 数值实验条件

选择二维正方形平板为数值实验模型,其参数如下:长度Lx=0.55m;宽度Ly=0.55m;ρc=4×106J/(m3·K);λ=47W/m·℃;传热系统的初始温度是20℃。假定热流边界的函数形式如下式

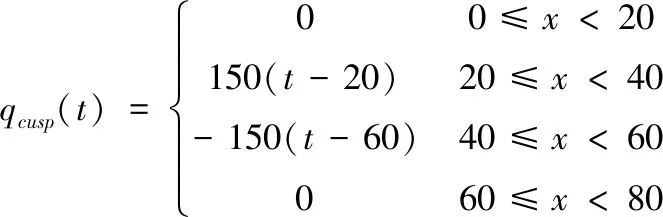
(22)

4.2 热流残差和相对平均误差

定义热流残差如式子(23)所示

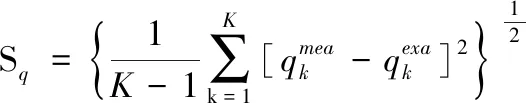
(23)

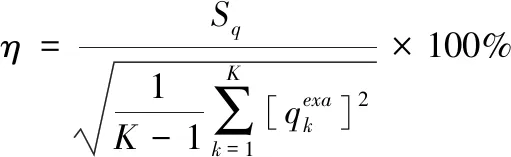
(24)

4.3 测点数目对反演热流的影响

图2和图3为固定测点位置距离x=Lx边界xp=0.005m,时间步数r=4,测量误差为σ=0.005时,不同测点数目下,脉冲形式的热流的反演值与真实值的对比,其中d分别为40和110。表1为不同测点数目下,热流残差和相对平均误差的对比。

表1 不同测点个数下,反演热流的热流残差和相对平均误差

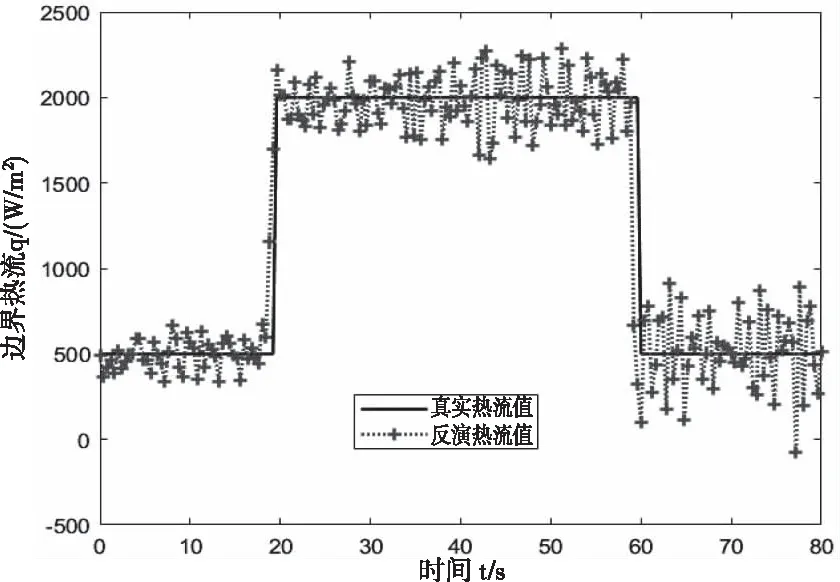
图2 测点数目为40时,反演热流值与真实热流值的对比

图3 测点数目为110时,反演热流值与真实热流值的对比

由图2和图3以及表1可以得出,测点数目的增加能够降低相对平均误差和热流残差。从反演热流值的振荡变化可以发现,测点个数的增长可以抑制振荡的幅度,这也说明本文所提算法对反演热流值具有滤波效果。

4.4 测量误差对反演热流的影响

图4和图5是不同测量误差下,脉冲形式的热流的反演值与真实值的对比。参数如下:测点位置距离x=Lx边界xp=0.005m,时间步数r=5,测点个数d=70,测量误差分别为σ=0.005和σ=0.01。表2表示不同误差下,反演热流的热流残差和相对平均误差的对比。

图4 在σ=0.005时,反演热流值与真实热流值的对比

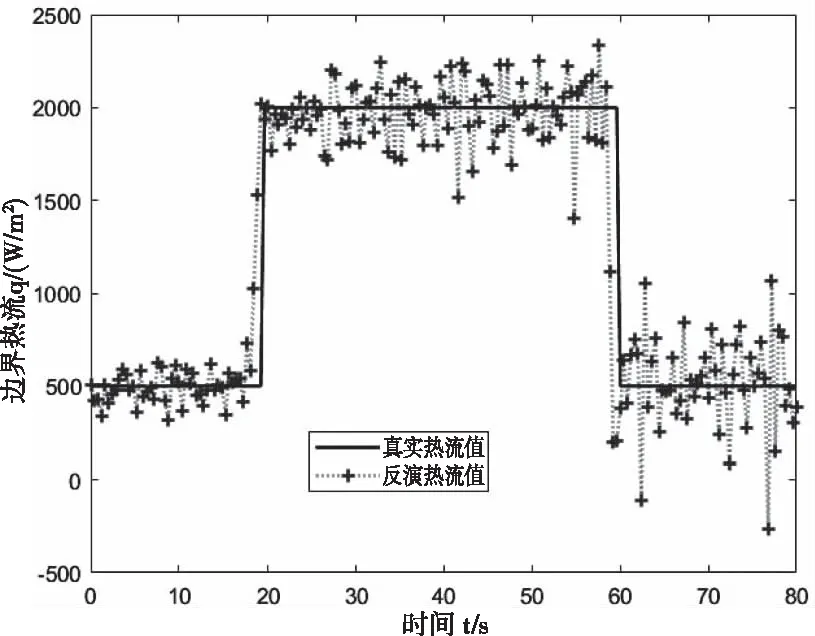
图5 在σ=0.01时,反演热流值与真实热流值的对比

由图4、图5和表3可得,随着测量误差的增加,反演的热流波动逐渐剧烈且波动幅度增加,同时反演热流的热流残差和相对平均误差不断增加,但准确度依然较高。

表3 不同未来时间步数下,反演热流的热流残差和相对平均误差

4.5 未来时间步数对反演热流的影响

在不同未来时间步数(r=3和r=7)下,固定测点位置距离x=Lx边界xp=0.005m,固定测点个数d=60,固定测量误差为σ=0.01时,给出了脉冲形式的热流的反演值与真实值的对比(如图6、图7所示),以及反演热流的热流残差和相对平均误差的对比(如表3所示)。

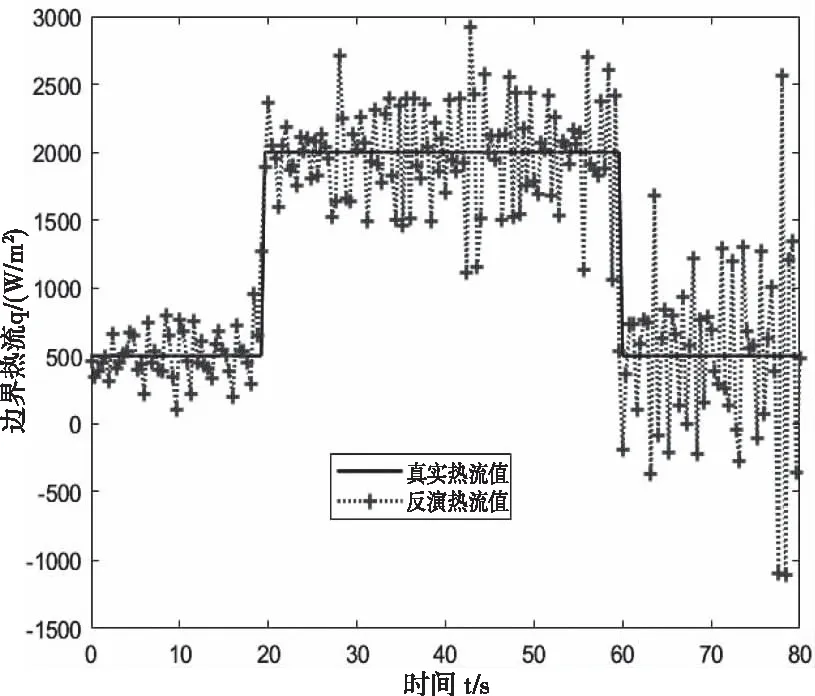
图6 在r=3时,反演热流值与真实热流值的对比

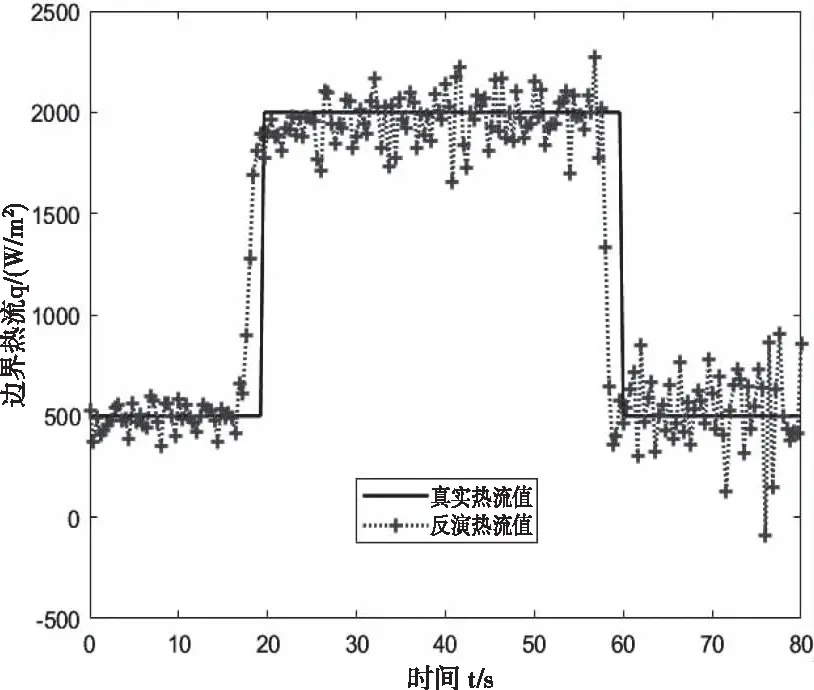
图7 在r=7时,反演热流值与真实热流值的对比

对比图6和图7、观察表3中对应项可知,适当增加未来时间步数可以有效减少相对平均误差和热流残差。在算法具体实施中控制好未来时间步数,能够有效降低反演热流的总体误差。

4.6 测点位置对反演热流的影响

测点位置距离x=Lx边界分别为xp=0.01m和xp=0.015m时, 调整未来时间步数可以得到反演热流值和真实热流值的对比情况(如图8、图9所示),以及不同位置的热流残差和相对平均误差情况(如表4所示)。其中测点个数为d=50,测量误差为σ=0.005。

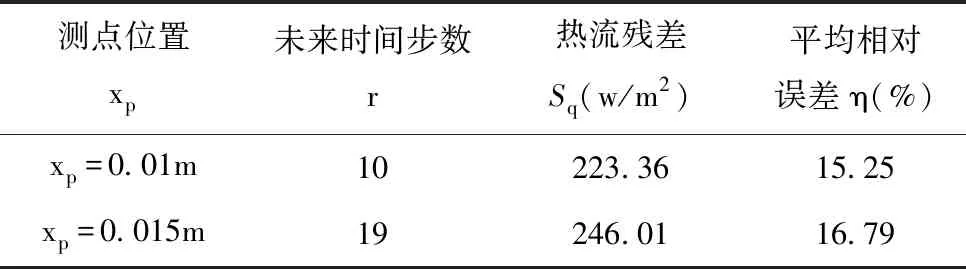
表4 不同测点位置和未来时间步数下反演热流的热流残差和相对平均误差

图8 在xp=0.01m和r=10时,反演热流值与真实热流值的对比

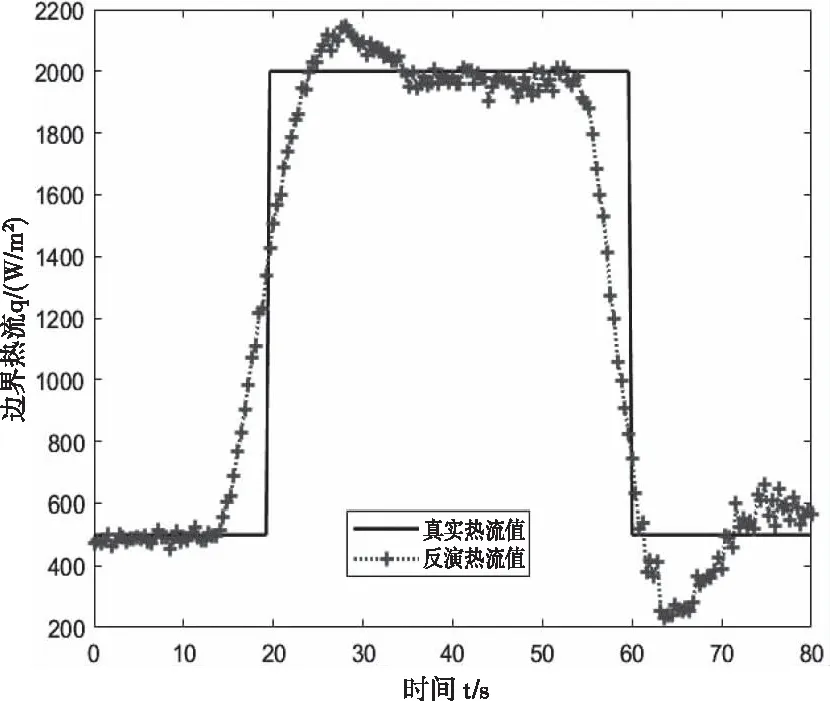
图9 xp=0.015m、r=19时,反演热流值与真实热流值的对比

从图8、图9以及表4给出的反演结果可以发现,测点位置离热流表面越远,所需要的未来时间步数r越大,即未来时间的温度信息越多。同时,未来时间步数的过度增加会导致平均相对误差的增大。在相同误差水平下,测点温度对表面热流的响应减弱,会导致反演的热流曲线偏离,使得反演结果误差增加,但热流的反演结果依然可观。

5 结论

本文针对二维非稳态导热系统边界热流反演问题,提出了结合顺序函数法以及阶跃响应系数概念建立预报误差模型的算法,其准则函数最大似然原理的应用,提高了反演的精度,增强了反演过程的稳定性。数值算例给出了在不同测点个数、不同测量误差、不同未来时间步数、以及不同测点位置情况下的反演结果,进一步证明了所提算法的鲁棒性和准确性。

采用本文方法,根据温度测点的位置和测量误差的水平,选取适当的测点个数和未来时间步数,可以有效地改善边界热流的反演效果。当距离热流边界较远或测量误差较大时,应该增加测点个数和未来时间步数,增加反演结果的准确性和稳定性。