基于轮廓局部线性拟合度估计的角点检测方法

张世征,刘 珊,黄万伟,郑 倩

(1. 郑州轻工业大学软件学院,河南 郑州 450001;2. 郑州西亚斯学院电子信息工程学院,河南 郑州 451150)

1 引言

角点作为图像重要的局部特征之一,在简化图像信息数据量的同时还保留了图像的关键特征,因而广泛应用于目标识别[1]、3D重建[2]、图像配准[3]、摄像机标定[4]和显著性检测等计算机视觉和图像处理任务中。角点检测算法从上世纪70年代首次受到关注,到目前为止,已经有超过百种不同的角点检测算法,根据其实现方法不同,大致将其分为三类[5]：分别是基于角点模型(Model-based),基于图像灰度(Intensity-based)和基于图像轮廓(Contour-based)的算法。本文关注基于图像轮廓的角点检测算法研究。

对于图像轮廓而言,角点通常理解为曲率极值点或边缘轮廓上轮廓方向急剧改变的点。基于轮廓的角点检测方法首先通过边缘检测器从输入图像中提取边缘轮廓,然后分析轮廓上的曲率值、形状变化信息或梯度方向来检测角点[5]。在1998年,Mokhartian等人[6]提出了著名的基于曲率尺度空间(Curvature Scale Space,CSS)的角点检测算法,利用曲线轮廓上像素点的曲率值计算角点响应函数。2007年,钟宝江等人在CSS算法的基础上进行改进,提出了直接曲率尺度空间(Direct Curvature Scale Space,DCSS)[7]算法,使用直接曲率尺度空间对轮廓曲线上各点进行建模计算该点是否为角点,降低了计算复杂度。随后张小洪[8]等人提出了一种多尺度曲率乘积(Multi-Scale Curvature Product,MSCP)算法,利用不同尺度乘积进行角点检测达到抑制噪声点或非角点处的曲率效果。2008年,He和Yung[9,10]提出了自适应阈值和动态支持域(Adaptive Curvature Scale Space,ATCSS)算法,该算法虽然降低了门限对性能的影响,但评估实验不充分,没有对仿射变换图像和噪声图像进行检测。文献[11-13]指出大部分基于CSS角点检测算法仍然存在对曲线的局部变化和噪声敏感、高斯平滑参数选取不合适的问题。基于此Awrangjeb等人[11]提出了弦点距离累积(Chord-to-Point Distance Accumulation,CPDA)算法,利用三个不同弦点距离累积值作为曲率点的响应函数。该算法虽然没有使用一阶和二阶导数但计算量仍然较大。2009年,Awrangjeb等人[14]提出了改进的快速版本F-CPDA(Fast Chord-to-Point Distance Accumulation),大大减少了计算量,但是Teng等人[15]指出Fast-CPDA算法的较高效率是通过牺牲平均重复率性能为代价。2010年,张小洪等人[12]提出梯度相关矩阵GCM(Gradient Correlation Matrices,GCM)角点检测算法。2015年,Teng等人[15]使用三角形弦长理论(Chord to Triangular Arms Ratio,CTAR)确定每个点的曲率值,与CPDA算法相比,CTAR平均重复率更高,检测速度更快。张小洪等人[16]分析了高斯算子在构造拉普拉斯尺度空间(Laplacian of Gaussian,LoG)的平面曲线上的尺度空间行为,得到了拉普拉斯比例尺度空间映射的解析表达式,基于新定义的统一角点模型、论证了平面曲线的拉普拉斯尺度空间行为。2017年,林薪雨等人[17]首先介绍了一种新的测量方法-轮廓的二阶差分(Second-Order Difference of Contour,SODC),基于SODC的分布特征,提出了两种新的方法,利用曼哈顿距离和欧氏距离计算轮廓点的响应函数,大大降低了计算复杂度。2019年,章为川等人[18]为了降低曲率估计对局部变换和噪声敏感,同时提高角点相距过近时准确性,提出了一种利用较大步长下曲率积以估计离散曲率的角点检测算法。

为提高轮廓角点检测算法对噪声和局部变化的鲁棒性,同时改善定位性能,本文提出了一种基于轮廓局部线性拟合误差(Local Linear Fitting Error,LLFE)度量的角点检测方案。与大多数直接估计曲率方法不同,本文采用估计曲线的局部弯曲程度来检测角点。该方法使用距离定义角点响应函数,同时采用较大的支持域,因此和CSS类方法相比对噪声的鲁棒性更好;此外本文采用正则化方案进一步增强了对仿射变换的鲁棒性。与5种典型的轮廓角点检测方法(CPDA[11]、F-CPDA[14]、Zhang[18]、LoG[16]和GCM[12])相比,本文提出的角点检测方法具有更好的检测性能和噪声鲁棒性。

2 本文方法

假设轮廓P由n个点构成,P={pj=(xj,yj),j=1, 2,…,n},(xj,yj)是点pj的笛卡尔坐标。定义Nm(pj)为轮廓的一个片段,Nm(pj)由pi-m和pi+m之间点集构成(为正整数),这里m为支持域半径大小,Nm(pi)={pi-m,…,pi,…,pi+m}。

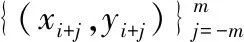
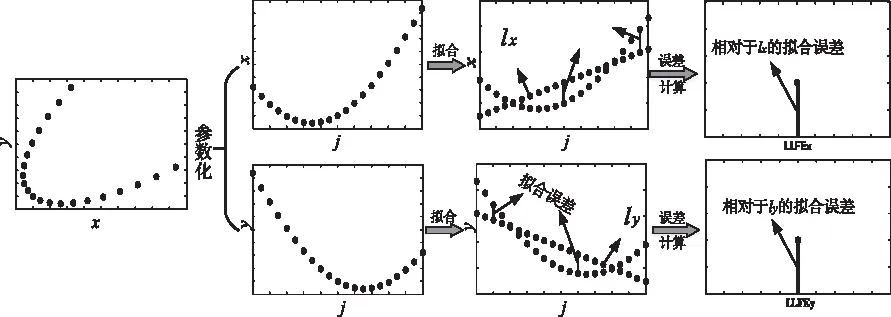
图1 LLFE的模型示意图

(1)

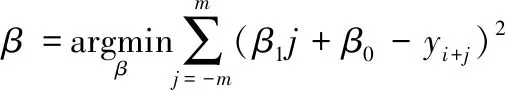
(2)

通过求解上述两个优化问题,可以推导出最优参数α*和β*为

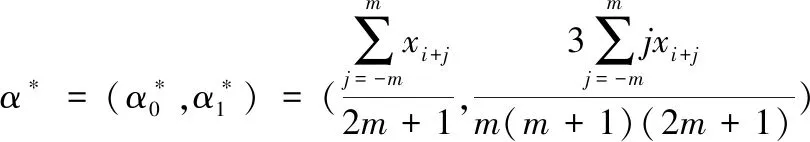
(3)

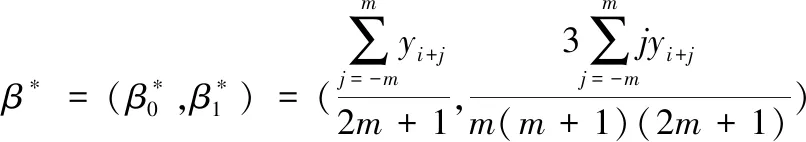
(4)

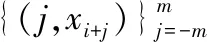
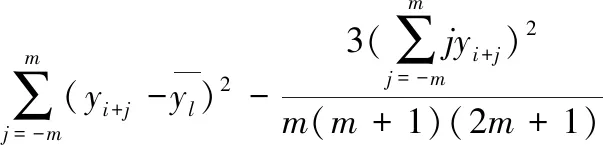
(5)

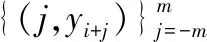
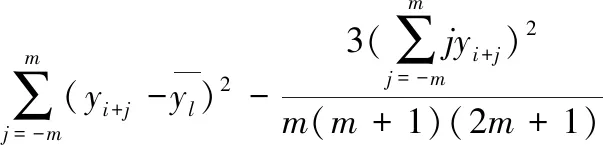
(6)

式中

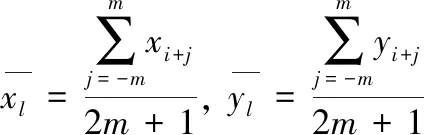
(7)

由于LLFEx或LLFEy单独不能准确反映线性拟合误差,而LLFEx、LLFEy之和能够反映线性拟合误差,因此本文将LLFE=LLFEx+LLFEy称作角点响应函数,值得注意的是,为了使LLFE在单尺度变换下具有更强的鲁棒性,进一步在LLFE上引入尺度正则化,式(8)表示基于正则化的LLFE：

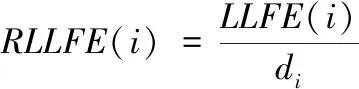
(8)

式中

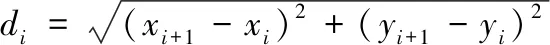
(9)

下面给出LLFE离散曲率在一幅飞机图像上的仿真。图2展示了使用LLFE算法对飞机轮廓的曲率响应图像,可以发现,在角点位置的曲率峰值异常突出,在非角点位置的曲率值接近0。图2的仿真结果验证了式(8)给出的拟合误差之和能够反映轮廓曲线的角点行为。

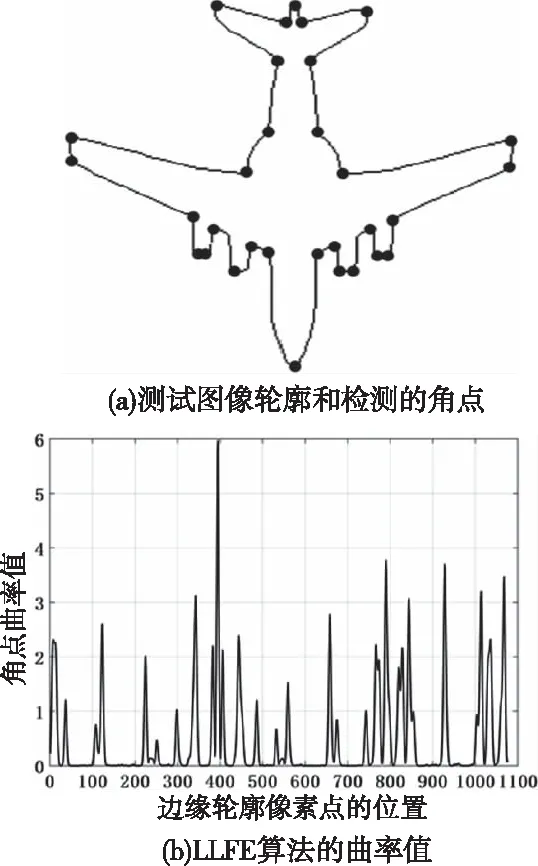
图2 LLFE在飞机轮廓上的曲率

LLFE算法流程图如图3所示,具体步骤如下:

图3 LLFE算法的流程图

第1步:使用Canny边缘检测器提取输入图像的边缘轮廓,并填充断裂边缘,获得相对完整的边缘轮廓,同时标识T-型角点。

第2步:使用均值为0,高斯核为σ的函数平滑,步骤1中提取的边缘轮廓,以及去除量化噪声和局部范围内的变化。

第3步:使用式(8)计算平滑去噪后边缘轮廓的角点曲率值,得到候选角点集。

第4步:进行非极大值抑制,将角点曲率值大于预设阈值T的点加入角点合集。

3 仿真与结果分析

本节通过相关实验,将提出的LLFE算法与五种经典的角点检测算法进行比较。下面介绍实验配置环境、数据集和评价标准。

3.1 运行环境

本文算法运行环境为i7-4790处理器,64位操作系统,内存8GB,主频3.60GHz以及MATLAB 2014b。

3.2 数据集

使用公开可用的GCM图像数据集,如图4所示,一共包括20幅不同的灰度图像,其中13幅为人工合成图像,7幅为真实世界图像,这些原始图像大部分选自标准数据库,包括经典的Block、House、Leaf等图像及一些简单的平面曲线。GCM数据集中的每幅原始图像经过5种不同的变换得到测试数据集,这五种变换类型是:

图4 GCM图像数据集

1)高斯白噪声变换。零均值高斯白噪声以 [0.005,0.05]范围,0.005为间隔加入原始图像。

2)旋转。在-90°至90°范围内以10°为间隔进行旋转变换。

3)一致尺度变换。x轴和y轴方向在[0.5,2]范围内以0.1为间隔进行同尺度的放大、缩小变换。

4)非一致尺度变换。x轴方向在[0.7,1.5]范围内以0.1为间隔进行放大缩小变换,y轴方向在[0.5,1.8]范围内以0.1为间隔进行放大和缩小变换。

5)旋转-缩放变换。原始图像同时进行3种变换:在-30°至30°范围内以10°为间隔进行旋转变换;x轴和y轴在[0.8,1.2]范围内以0.1为间隔进行同尺度放大、缩小变换。

3.3 评价准则

使用两个评价准则进行性能分析:①平均重复率和定位误差[11];②精确度和定位误差[11,19]。

3.3.1 平均重复率评价标准

Awrangjeb等人[11]提出了一种鲁棒的评估方法,该方法不涉及人工干预,适用于任何规模的数据集,使用平均重复率和定位误差评价标准来衡量角点检测器的鲁棒性。平均重复率Ravg表示原始图像和经过尺度变换后图像之间的角点重复率,表达式如下

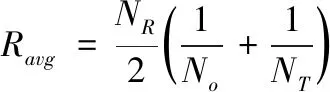
(10)

其中,No表示原始图像中检测到的角点个数,NT是测试图像检测到的角点个数,NR表示原始图像与测试图像之间重复的角点个数,Ravg值越大表示算法的鲁棒性越优异。

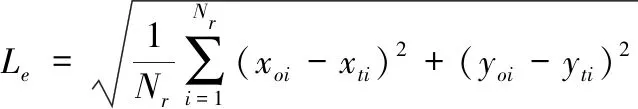
(11)

其中,(xoi,yoi)和(xti,yti)分别代表原始图像和测试图像中第i个匹配角点位置,定位误差越小表示角点定位越精确。

3.3.2 精确度评价标准

Mohanna和Mokhtarian[19]提出了基于精确度(Accuracy,ACU)的评估标准,该方法表示原始图像真实角点和测试图像角点的匹配率。No表示测试算法检测到的角点个数,Ng表示真实角点(ground truth)个数,Na表示真实图像角点和测试算法检测角点之间匹配的个数。精确度可由式(12)表示

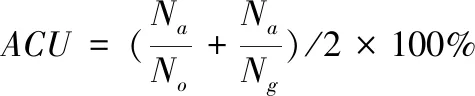
(12)

LE[11]是基于两点之间欧式距离定义的均方根误差。表达式如下

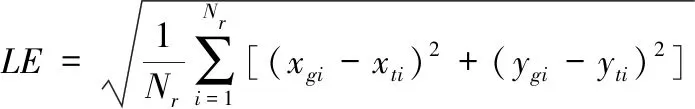
(13)

其中,Nr表示真实角点和算法检测角点匹配的个数,(xgi,ygi)是真实角点中第i个匹配的位置,(xti,yti)是检测角点第i个匹配的位置。

3.4 实验结果分析

3.4.1 参数选择

LLFE角点检测算法主要涉及三个可调节参数:支持域大小(Region of Support,RoS)、高斯标准差(σ)和曲率阈值(Threshold),本文采用一次只调整一个参数,同时固定另外两个参数的方法来获取最优参数。为了公平比较,对比实验中其它角点检测算法也执行相同的最优参数选择方案。需要指出的是,按照文献[11,12,20]中设置,基于精确度准则的Canny边缘检测器的阈值设置为低=0和高=0.35,基于平均重复率准则的Canny边缘检测器的阈值设置为低=0.2和高=0.7,本文采用相同的Canny边缘检测子参数。表1展示了基于平均重复率评价准则选取的最优参数。表2展示了基于精确度评价准则选取的最优参数。

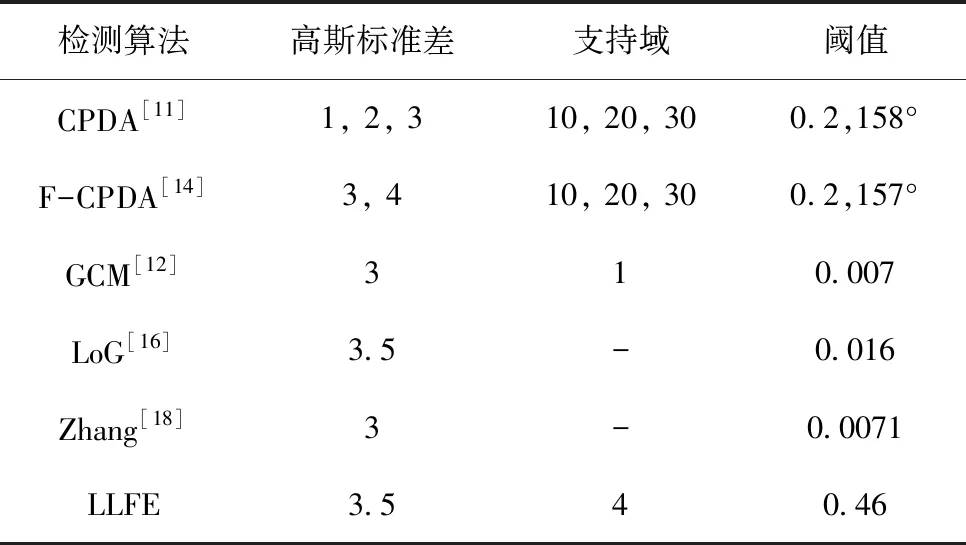
表1 六种对比算法基于平均重复率评价标准的参数设置

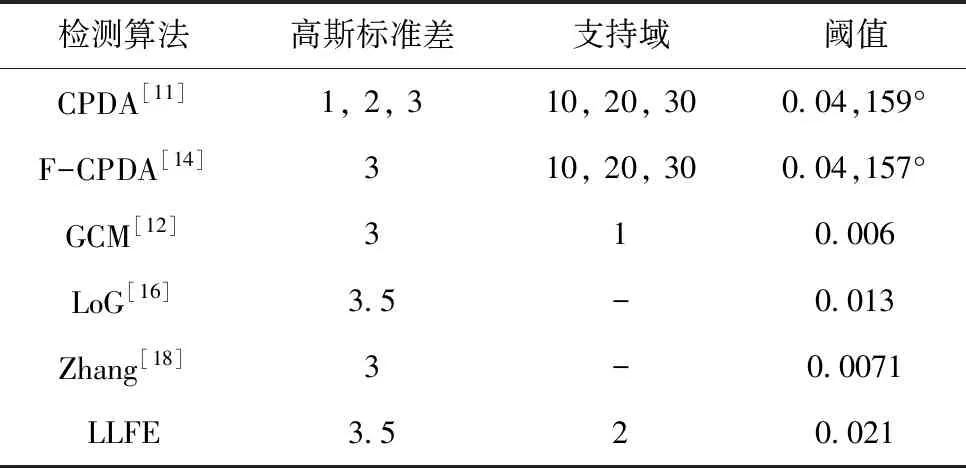
表2 六种对比算法基于精确度评价标准的参数设置

3.4.2 高斯噪声和仿射变换实验

本文将提出的LLFE角点检测算法与CPDA[11]、F-CPDA[14]、Zhang[18]、LoG[16]和GCM[12]算法进行高斯噪声和仿射变换实验比较。图5和图6显示了六种算法关于噪声和仿射变换的平均重复率和定位误差。从图5和图6可以看出,随着高斯白噪声的增大,所有算法的稳健性逐渐降低,但LLFE算法下降趋势明显低于所对比的其它算法,表明LLFE算法对噪声的干扰具有较强的稳健性,另外,F-CPDA和Zhang算法随着噪声的增加,稳健性下降比较快,表明F-CPDA和Zhang算法对噪声较为敏感;在旋转变换下,LLFE算法获得最高的平均重复率和最低的定位误差;在一致尺度变换下,本文算法获得了优异的平均重复率,而在定位误差方面,CPDA和F-CPDA相比更低一些;在非一致尺度变换下,LLFE算法获得最高的平均重复率和最低的定位误差;最后在旋转尺度变换下,LLFE算法同样获得最高的平均重复率,本文算法和LoG算法具有最好的定位性能;从五种变换的平均结果来看,本文提出的LLFE算法表现出最高的平均重复率和最低的定位误差(定位误差越小,检测性能越优异)。实验结果表明,在基于平均重复率评价标准下,本文提出的LLFE角点检测算法具有最优异的鲁棒性。

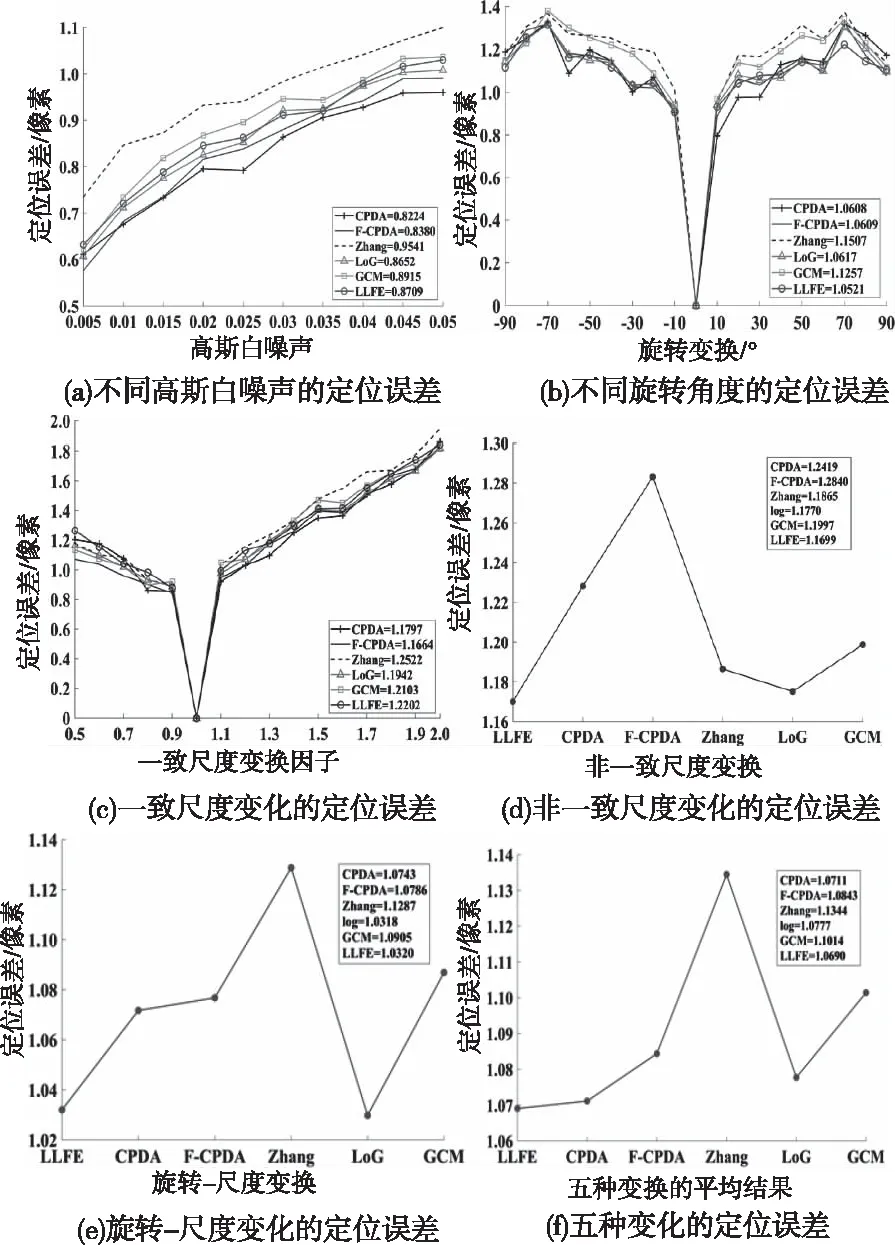
图6 基于平均重复率标准下的定位误差

图7和图8显示了六种算法关于噪声和仿射变换的精确度和定位误差。由图7可知,在添加不同高斯白噪声和非一致尺度变换下,LLFE算法具有最高的精确度;旋转、一致尺度变化和旋转-尺度变化下LLFE算法与LoG算法精确度相似。由图8可知,在添加不同高斯白噪声变换下,LLFE算法也能优于CPDA、FCPDA和Zhang算法;在不同的旋转角度变换下,LLFE算法也取得了优异的检测结果。在一致尺度变换下、非一致尺度变换和旋转-尺度变换下LLFE算法定位性能比CPDA、GCM和Zhang算法表现出色;从平均结果可以看出,LLFE算法定位误差在六种算法中排名第二。根据噪声和仿射变换的精确度和定位性能结果,可以得出本文提出的LLFE算法具有较高的检测精度和良好的定位性能。

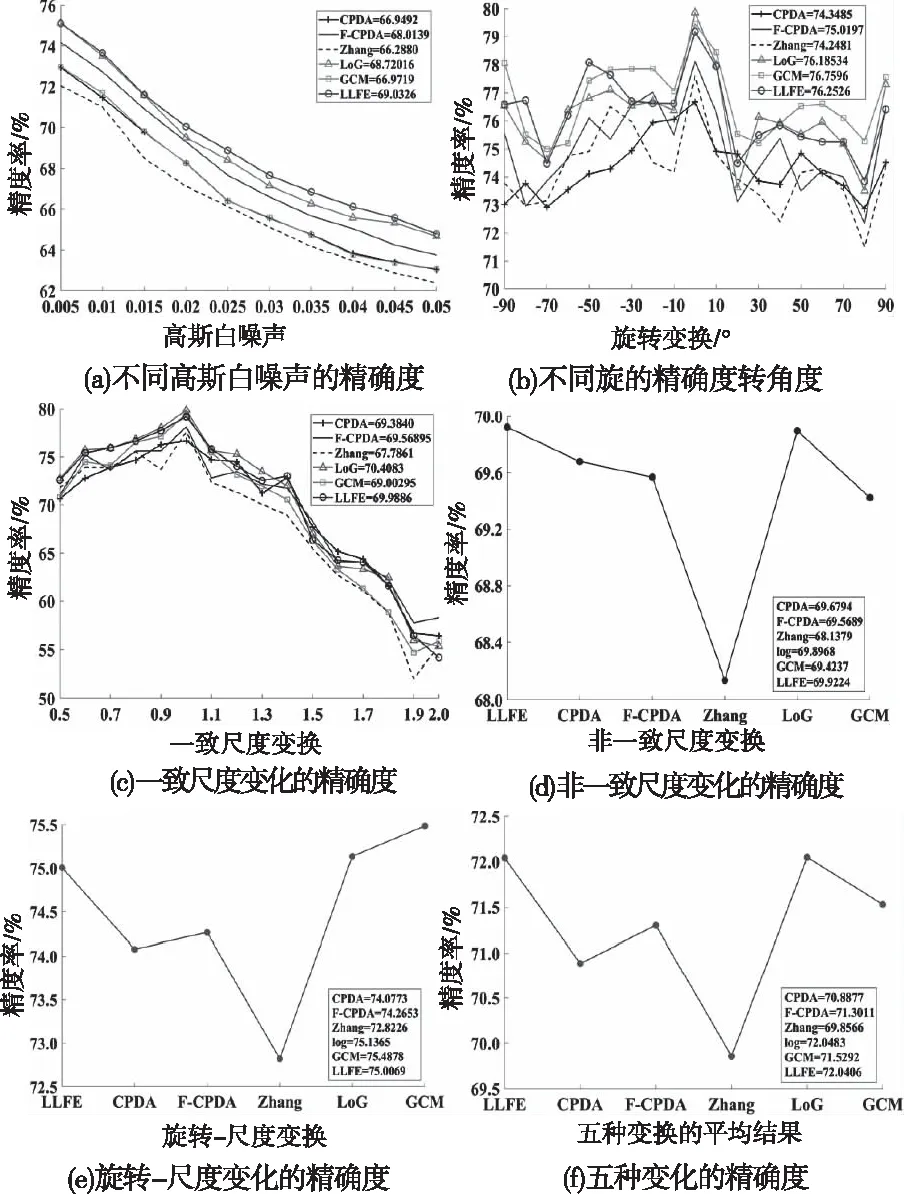
图7 六种算法的精确度

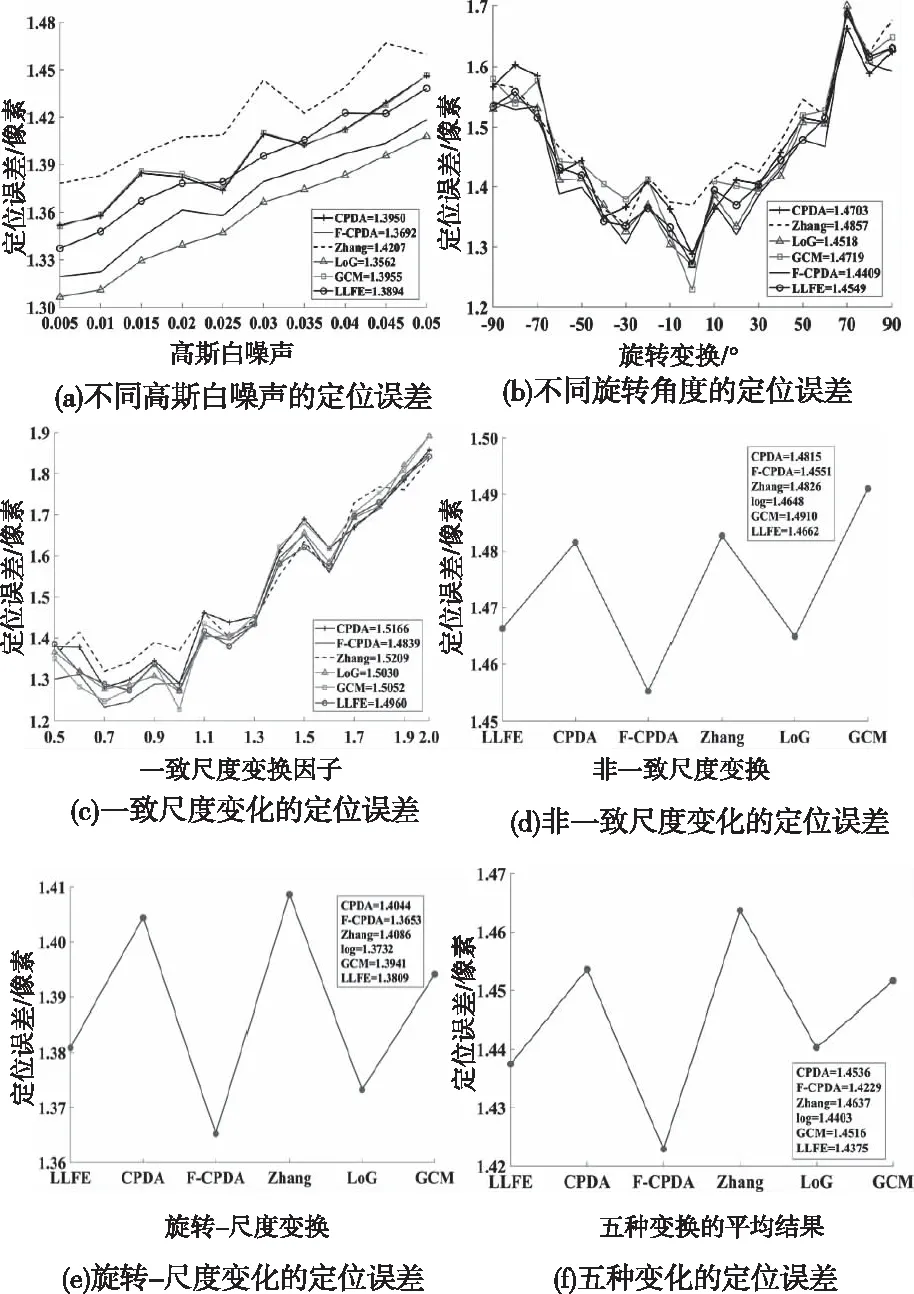
图8 基于精确度标准下的定位误差

3.4.3 角点检测实验

对GCM图像数据集中每幅测试图像,执行算法10次,计算平均执行时间。如表3所示,在6个检测器中,本文提出的LLFE算法执行速度比较快,约是CPDA检测角点速度的3倍,这主要是因为CPDA算法曲率计算需要进行多次平方根运算[17],同时LLFE比F-CPDA、LoG和GCM算法检测速度也更快,这验证了LLFE算法的高效性。

表3 角点检测时间对比(10次随机实验的平均结果)

图9给出了LLFE算法在8幅图像上的角点检测结果,可以看出,对于人工合成图像,几乎所有的真实角点都能被检测到,在真实图像中,有少数角点被遗漏。这些结果验证了LLFE算法的准确性。

图9 LLFE算法的角点检测结果

4 总结

本文提出了一种新颖的基于轮廓局部线性拟合误差的角点检测算法,与大多数直接估计曲率的检测算法不同,本文采用最小线性拟合误差估计曲线局部弯曲程度,整个算法计算过程使用距离而不是导数,故对噪声和局部变换不敏感,同时采用正则化方案进一步增强了对一致尺度变换的鲁棒性。基于平均重复率和精确度两种不同评价标准的实验结果验证了LLFE角点检测算法的优异检测性能和对噪声较好的稳健性,但在角点检测运行时间方面,LLFE算法与文献[18]还存在一定的差距。同时作为一种基于轮廓的角点检测算法,LLFE对边缘检测算法性能具有高度依赖性。因此下一步工作将会对提出的LLFE算法进行不断优化,提高角点检测速度,扩大适用范围,使其应用于更多的计算机视觉和图像处理任务。