拉普拉斯修补矩阵下图像渐晕高效复原方法

吕 晶,薛亚非,刘益新

(1. 南京师范大学中北学院,江苏 丹阳 212300;2. 南京大学,江苏 南京 210023)

1 引言

图像是人类获得信息的主要方式,具有简单、直观、清晰等优点,在各个领域中都有着举足轻重的作用。随着时代进步和科学技术的不断发展,人们对于影像的认识也越来越深刻,与此同时对图像品质的要求也越来越高,数字图像处理技术已逐渐成为业界关注的焦点。其中图像还原是从退化模糊图像中提取图像的一项重要技术。影像模糊或渐晕通常受到晃动影响,因物件与摄影机间的相对移动,导致物体成像模糊不清,从而给人类的生产、生活甚至是科学研究等带来诸多的不便。图像渐晕复原是当前研究的热点之一,在很多科学研究和工业生产中有着举足轻重的作用。

白亮等人[1]研究的层级融合自适应复原法,将不同层次的图像特性融合,提高了图像的总体结构,注意机理增强了模型自适应能力,实现了不同层次的图像动作状态的融合,提高了主观视觉质量;王向军等人[2]提出一种循环注意力复原法,利用深度可分离卷积有效地降低模糊图像的参数量,合理分配图像资源,计算边缘损失,修复边缘细节信息,实现图像的复原处理。但上述两种方法都在图像去噪效果不够理想,或多或少将原本信息也去除掉,导致复原图像内有效信息量降低。

为解决上述方法存在的问题,提出基于拉普拉斯修补矩阵的渐晕复原方法。利用调和去噪模型将图像中存在的噪声干扰有效去除,并对图像保真,在盲区模糊处理中,利用先验信息计算后验概率,通过拉普拉斯修补矩阵估算复原最优值,实现渐晕图像的深度复原。

2 图像渐晕复原调和去噪模型构建

为保证渐晕图像在复原过程中,能保持良好的清晰度和边缘细节,建立图像的调和去噪模型[3],基于L2范数,构建图像四边形扩散降噪模型[4],具体的函数表达式为:

(1)

式中,u表示原始图像,u0表示含噪声的图像,Ω表示图像的整体区域范围,λ表示拉格朗日乘数[5],|∇u|表示去噪模型中的梯度算子模值。通过上述函数模型可以实现变分推导,求解出拉格朗日方程,在此基础上利用梯度下降流,将方程转换成偏微分方程式:

(2)

其中∂表示梯度下降流的微分参数[6],此时图像中各个方向上同性扩散对应的调和去噪模型可以实现离散化处理:

(3)

式中,Δt表示离散处理的迭代时间步长,w表示原始图像坐标ui,j上的8个领域点,根据离散化处理后的模型可以看出,噪声向图像中各方向上扩散的能力基本相同,这样会在去噪过程中使边缘模糊化。

在图像中,任何象素点都有一个较稳定的边界方向和梯度,因为扩散降噪模型在每个方向上的扩散能力基本上是一样的,所以不能充分地反应沿边缘或斜坡方向发生的扩散系数差,所以,在降噪过程中,图像边缘很容易变得模糊,因此,采用拉普拉斯算子,该算子在边缘上扩展,既能更好地抑制噪声,又能有效地防止边界的破坏。

在图像中相对平滑区域中,边缘和梯度的扩散系数值相对来说较大,既满足降噪的需求又能有效的消除图像噪点的阶梯效应,在图像的边沿上,扩散系统的数值维持较大值,同时,在斜率方向上要保持一个很小的数值,这样可以防止图像的边缘出现严重模糊。在精确地确保边缘细节不会受到影响的情况下,对图像中的边缘细节适当处理。利用拉普拉斯算子处理,完成锐化过程,同时保持了图像的背景信息,∇2表示拉普拉斯算子,其对应的模型表达式如下所示:

∇2u1(i.j)=(u(i,j))xx=ui-1,j-2ui,j+ui+1,j

(4)

∇2u2(i.j)=(u(i,j))xy

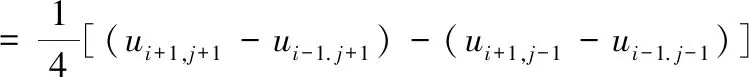
(5)

∇2u3(i.j)=(u(i,j))yx

(6)

∇2u4(i.j)=(u(i,j))yy=ui,j-1-2ui,j+ui,j+1

(7)

(8)

通过拉普拉斯算子的计算,将ROF模型、L2范数模型和拉普拉斯算子与权重系数相结合,形成一个完整的RHI二阶偏导求和模型:

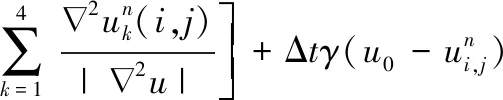
(9)

式中,τ1和τ2表示各个模型之间融合的加权系数,γ表示改进过后的图像保真项系数,ε小值正数。

RHI模型经过多次的迭代计算最终逐渐收敛得到正解:

wn(i,j+1)-4wn(i,j)]

(10)

3 图像盲去模糊

对去噪后的图像采取盲去模糊处理,大多数都是利用图像和卷积核控制先验信息来完成图像的空间约束,但实际过程中存在图像各方向上扩散高度的不适应性,为此在研究图像渐晕复原方法时,为了提高整体的稳定性,利用先验信息计算求得后验概率最大解。假设图像中模糊的观测点y,利用贝叶斯规则计算图像模糊问题[7]的后验分布情况:

P(k,x|y)∞P(y|k,x)·P(x)·P(k)

(11)

式中,N表示渐晕图像中包含的像素数量,ζ表示像素的高斯分布形态,σ2表示渐晕图像中高斯噪声的方差数值,P(x)、P(k)分别为渐晕图像和其对应模糊核的先验信息。通过给出合适的渐晕和模糊核的统计特性,可以得到更加全面的图像。

在最大后验估计值的基础上,对渐晕图像盲去模糊主要分成两个步骤:一是估计渐晕图像的模糊核[8],二是估计渐晕图像中间层的清晰区域,交替迭代上述步骤,实现对图像清晰区域和模糊核同时估计的目的。假设模型中均为高斯白噪声,此时渐晕图像的最大后验概率模型可表示为:

(12)

为了方便计算,将式(12)简化处理,得出实际的能量函数[9]：

(13)

式中,μ表示先验信息中正则项对应的权重系数,交替迭代下面式(14)和(15)可以求解式(13):

(14)

(15)

此时,将式(14)作为渐晕图像的非盲去卷积,式(15)作为渐晕图像的估计模糊核,当二者对图像先验信息以及空间的真实约束力不同时,最终求解得到的中间层图像也会大不相同,从而直接影响到图像的估计模糊核。

4 图像渐晕复原算法的实现

考虑到先验信息以及空间的真实约束力不同问题,使用基于拉普拉斯修补矩阵的影像强化实现最终复原算法。图像渐晕恢复是对图像去模糊,与影像强化相似,影像恢复技术其终极目标是提高一个特定的影像质量,而图像增强则是一种主观的图像恢复过程,而对图像的渐晕部分复原中大多数程序都是客观的,图像恢复是一种尝试利用某些已知的退化现象重构或者恢复已退化的技术,所以,图像渐晕复原技术就是对退化建模,采取反向处理[10]

拉普拉斯修补矩阵是图像中经常用到的一种矩阵模型,由于图上的结点对应的是自变量,信号函数是“结点域”上的函数,而图上结点之间并没有这种全序关系,因此考虑所以邻居结点,使用拉普拉斯修补矩阵对各个分量的二阶偏导求和,有效地实现图像的复原和补充。假设一个图像中包含多个定点,可将其定义为L=D-A,其中D表示的是图像中的度矩阵,A表示图像相邻的矩阵。

通过图1可知拉普拉斯修补矩阵具备对称性,将其转换为正则化的拉普拉斯修补矩阵:

图1 图像退化/复原过程模型

Lsym=D-1/2LD-1/2=I-D-1/2AD-1/2

(16)

为了最大程度恢复原始的图像内信息,通常的做法是用数学方法来确定最优标准答案,对所需结果的最优值估算,其中包含噪声干扰、大气环境等影响图像质量的重要因素,以及成像装置和目标对象之间的相对运动等,因此,要建立一个统一图像降级数学模型,这种模式很难实现,为此选用线性位移数学模型来描述图像退化类型[11]。

利用数学模型,将真实的降维过程分解为一个退化函数和一个加性噪声项,如图1所示。

图1中,f(x,y)表示原始的清晰图像,g(x,y)表示经过退化后的图像,给定图像g(x,y)和对应的退化函数[12]H一定信息,在此过程中加入适量的噪声项η(x,y),对渐晕图像复原主要是为了获取接近于原始图像的估计值f′(x,y),这种无线逼近的估算可以看作是对渐晕恢复的最后结果。

建立图像渐晕复原的自适应拉普拉斯模型[13-14]：

(17)

式中,实际的渐晕状态扩散控制系数p(∇u)的数值范围为1≤p(|∇u|)≤2,该数值主要取决于等照度线的曲率k和梯度∇u两个因素共同决定的:

(18)

式中:

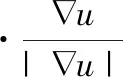
(19)

当p(|∇u|)为常数值时,搭建的自适应拉普拉斯图像渐晕复原模型函数[15]可表示为:

p(|∇u|)=p(|∇u|)|∇u|p(|∇u|)-1+

(ln|∇u|)p′(|∇u|)|∇u|p(|∇u|)

(20)

根据式(20)的计算结果可以得出,所提方法在图像平滑区域部分取值无限接近于2时,图像渐晕部分可以实现快速平滑;在图像的边缘部分,若取值接近于1的情况下,模型将沿着等照度线完成扩散,并在指定的梯度方向上采取平滑处理,抑制和削弱图像的渐晕,更大程度的保留图像细节。

5 实验分析

为验证基于拉普拉斯修补矩阵的渐晕复原方法(所提方法)的实际性能,选择一张像素标准的灰度图像作为实验图像,如图2所示。可以看到原始实验图像中包含大量噪声,且模糊程度和渐晕程度均严重影响图像的实际观赏性。

在实验过程中选择Tensorflow1.2深度学习框架,判断训练和测试结果,实验选用的硬件配置为Ubuntu16.04操作系统,为保证对图像分辨率的判断准确,选择NVIDIA GeForce GTX 1080 Ti显卡。

基于已有的超分辨率,将均值为0、标准方差为10的高斯白噪声添加到原始图像中,分别利用层级融合自适应复原法、循环注意力复原法和所提方法对原始图像渐晕复原操作和验证。

通过人眼观察的主观判断评定图像复原质量,利用三种不同方法对原始模糊图像去噪处理,结果如图3所示。

图3 三种方法下图像去噪效果

从图3中可以清晰的观察出,经过层级融合自适应复原法去噪后的图像跟原始图像相比,清晰了一些,但没法做到完全去除噪声影响;循环注意力复原法的去噪效果相比层级融合自适应复原法要好,图像经过去噪后更加清晰,但会发现循环注意力复原法在去噪过程中将图像的对比度和曝光度过度提高,导致图像细节虚化,需要从后续的去模糊和复原图像中确定循环注意力复原法的实际效果;所提方法对图像去噪处理后,图像中的噪点干扰基本消失,且一定程度上优化了图像的明暗对比度,但是并未过度,方便后续对模糊内容的甄别。

利用三种不同方法对图像深度去模糊处理,实现图像渐晕复原,实验结果如图4所示。

图4 三种方法下图像渐晕复原效果

根据图4可以看出不同方法针对图像去模糊后的感官效果,循环注意力复原法效果优于层级融合自适应复原法,但通过所提方法完成渐晕复原后的图像,相对其它方法更加清晰,噪声干扰少,渐晕及模糊情况得到明显的改善,且图像丢失信息。

进一步针对图像复原方法的客观量化采取实验,通过对指定量的分析,确定方法的实际性能,分别对三种方法的复原模型采取200次的迭代计算,记录下图像渐晕复原过程中损失函数随着时间的变化情况,实验结果如图5所示。

图5 不同方法模型的损失函数迭代曲线

从图5的试验结果可以看出,在层次融合自适应恢复方法中,损失函数的训练值存在很大的波动,为了获得最后的收敛,必须多次迭代;循环注意力复原方法的模型有一定的波动,但总体来说,与层次融合自适应恢复法相比,更加的稳定,在训练的前期,模型可以快速的进入收敛状态,而在训练的时候,则是比较平稳的;在三种方法比较中,所提方法的波动平缓,且在很小的训练量下,就可以获得最佳的图像恢复方案,并具有良好的性能。

6 结论

采用拉普拉斯算子完成图像渐晕修复的过程中,对图像噪声抑制,以区分光滑和边缘区域,在对边缘区域处理后,可以有效地抑制梯度噪声,并使边缘方向的扩散增大,减少边缘模糊情况发生。结合模型优势,利用拉普拉斯算子提高图像细节,实现图像去模糊和渐晕修复,达到图像保护的目的,经实验证明所提方法可行有效,迭代次数少,效果稳定清晰,鲁棒性好。