强化学习理论下农村物流配送最优路径规划

韩翔宇,李 慧,梁 硕,王书强

(1. 邯郸学院河北省光纤生物传感与通信器件重点实验室,河北 邯郸 056005;2. 邯郸学院信息工程学院,河北 邯郸 056005;3. 河北工程大学,河北 邯郸 056038)

1 引言

随着农产品进城与农用品下乡的数量增多,进而增加物流的订单量。但这些订单较为分散,同时合作的物流公司较少,车辆配送时会出现单程、倒流与迂回等运输情况,这大大增加配送货车行驶距离,进而增加运输成本[1-2]。假设在配送前获得最优路径,可以缩短物流配送路程,节省大量配送时长时间,降低物流总成本,提高物流配送效率[3-4]。

为此,关于配送最优路径的问题,诸多学者提出各自的解决办法。如李学现等人[5]提出考虑能耗动态变化的露天矿卡车运输最优路径规划方法,根据路段运输功率,得出路径各节点间的转移概率,并通过自适应动态因子调整蚁群信息,结合交叉算子与变异算子增加种群类别,进而提升该算法的局部收敛能力,最终选出最优路径。王雷等人[6]提出智能网联下无人驾驶汽车配送路径优化方法以配送车辆最小成本为目标,运输时长为限定条件,建立配送车辆行驶路径模型,并采用多种群遗传算出路径规划最优解,进而得出最优路径策略。

通过综合上述优势,采用强化学习规划农村物流配送最优路径,该方法能够进一步缩短物流运输时长,减少物流配送路径总长度,进而降低配送车辆的总成本。

2 最优路径规划

2.1 农村物流配送路径函数模型

2.1.1 问题描述

假设有a个配送中心A,b个顾客,配送车辆根据配送中心指令完成各自任务,并不会产额外费用。若配送车辆过早与过晚到达目顾客所在地,就会产生额外成本。为此,增加1个虚拟配送中心o,o产生不需要任何费用。物流配送车辆从o出发,经过A,再到达顾客所在位置,进行取货与送货服务,再从A回到o[7]。

2.1.2 模型参数

设定o描述为虚拟配送中心;B={1,2,…,b}描述为顾客点集合;C={1,2,…,c}为农村物流配送中心车辆;集合N=A∪B为全部点的集合;Q描述为配送车辆极限满载量;sb′与pb′分别代表顾客b′的送货与取货的需求量;Sb″b′k与Pb″b′k分别代表配送车辆k从顾客b′到b″的车辆取货与送货的总质量;db′b″代表b′到b″之间的距离;[tb″e,tb″,i]描述为b″的配送使用时间;ϖ1与ϖ2分别代表配送车辆早到与晚到的惩罚系数;e1是配送车辆出行一次固定行驶成本;e2是车辆单位行驶成本。

农村物流以总配送总成本最小为目标,建立配送函数模型为:

(1)

其中,minZ表示车辆配送最小总成本;xb″b′k表示配送车辆k从顾客b′到b″的服务次数。

各顾客点只可进行一次服务,其表达式如式(2)所示:

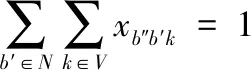
(2)

顾客点需要送货与取货的量分别用式(3)与式(4)表示。

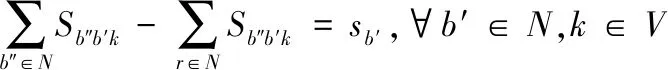
(3)

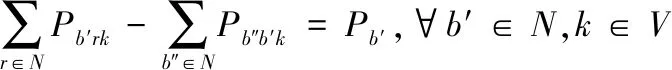
(4)

式中,V表示总配送车辆。

在配送车辆满载极限之内,顾客点取货与送货的量分别用式(5)与式(6)描述。

(5)

(6)

配送车辆载货极限值表达式如式(7)所示。

(7)

配送车辆行驶状态,即每一台配送车辆都是从虚拟配送中心驶出,并驶回该中心,其表达式为:

Sb″b′k+Pb″b′k≤Qxb″b′k,∀b″,b′∈N,k∈V

(8)

式(9)与式(10)描述为决策两个变量公式。

(9)

(10)

2.2 强化学习环境设计

在物流配送函数模型基础上,结合强化学习规划农村物流配送路径[8-9]。如果配送系统中存在一个智能体,经过一系列运作,给出配送路径的解决策略。在每一个环节中,智能体都能实时收到系统状态数据,并根据已知信息与策略,指导其作出相应动作。该过程就是通过强化学习给出智能体的奖惩与状态变化。通过车辆路径实例来训练智能体,并根据奖惩函数评估智能体给出的解决方案,并对其状态相应改进。

2.2.1 奖励函数设计

奖励函数设计是智能体训练核心的部分。其不是为了得到某一时刻的最大化奖励,而是为了获得长期最大化的累计奖惩。通常在计算农村物流配送最优路径时,易陷入局部最优解,无法保证配送路径最短,增加配送车辆行驶的成本,为此基于强化学习设计一种奖惩函数,通过不断动态调整奖惩函数,使训练模型达到最佳效果[10]。

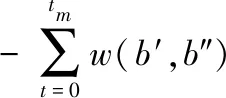
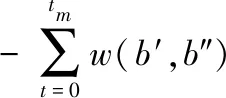
(11)

当中,α1与α2均为负的常数;ηt表示t时刻的状态。强化学习与其它学习方法不同,其是根据估计数值的情况来改进模型参数,奖励函数更新强化学习策略网络与价值网络,智能体按照这些奖励信号不断更新,进而得到期望结果。

2.2.2 状态转移函数

智能体经过强化学习,能够根据目前状态情况选取恰当的动作,强化学习环境更新智能体的下一个状态,反复进行这个过程[12-13]。可发现状态的更新与环境有关,经过模拟强化学习环境,即可获得时间窗下农村物流配送车辆路径的状态转移函数。

假设Xt与Gt表示配送车辆路径强化学习的系统的两个状态。强化学习的动作就是在序列的末尾增添一个客户点,b′作为在t时截取序列的顶点,Bt描述在t以前客户的序列。如果该过程在tm时停止,代表该时刻没有需求的顾客,即全部顾客点的需求为0。在t时刻智能体会获得来自局部信息与全局信息,也就是Xt,Gt,Bt。当中Bt为历史轨迹,通过模型即可获得各客户点的条件概率分布,即P(b″=i|Xt,Gt,Bt)。再利用概率分布策略选取b″客户点加入当前序列的末端,并更新系统的状态,即

(12)

当中,w(b′,b″)描述为b′到b″的配送车辆行驶所用的时间。利用欧式距离算出配送车辆距离与车速,即:

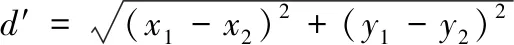
(13)

配送车辆装载容量更新过程为

(14)

无需考虑w(b′,b″)是否为负,因为系统会屏蔽需求超过该配送车辆的装载极限容量的客户点。则需求更新过程为:

(15)

利用强化学习环境获得的状态转换为St→Si+1,强化学习过程是通过不断的测试、环境交互,从环境的奖惩中学习决策策略与状态的价值,不断迭代优化模型参数。

2.3 策略网络训练

采用带有回滚基准训练策略网络,可以得出各智能体的累计回报率,并根据该结果预测策略的梯度,完成各智能体策略的训练[14]。设定e表示农村物流配送的1个实例;θ表示实例策略网络;pθ(πt|e)描述为θ输出个智能体各动作概率矢量总和,并经过采样选取输出的联合策略,即

πt=sample(pθ(πt|e))

(16)

基准网络θ′是根据其输出的动作概率向量pθ′(πt|e),并以贪婪选取形式得出联合策略,即:

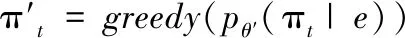
(17)

经过蒙特卡洛计算策略的期望累计回报值,即

L(θ|e)=Epθ(e)[R(π)]

(18)

当中,Epθ(e)表示期望概率矢量;R(π)表示策略π={π1,π2,…,πT}的累计回报。根据带有回滚基准求解策略的梯度,并结合梯度下降的算法更新策略网络相关参数,计算过程为:

ΔθL(θ|e)=-Epθ(π|e)[(R(π)-R(π)′))×Δθlgpθ(π|e)],

θ=Adam(θ,ΔθL(θ|e))

(19)

通过θ′分析e的难易程度,进而缩小训练网络时梯度方差。基准网络按照回滚形式更新,每一次训练结束后都会将θ与θ′对比分析,假设θ明显优于θ′,就需要对θ′回滚更新,即θ′→θ。

2.4 动作选择与全局搜索策略

通过多次强化学习的策略网络已具有良好的决策能力,动作选取策略按照网络输出的概率矢量,选出最佳动作[15]。选用贪婪与采样两种方式选取最佳的动作,即:

1)贪婪动作选择是根据策略网络,每一步都是选取网络输出最大概率的动作;

2)采样动作选取策略依旧以策略网络输出概率当做采样概率分布,在该分部上进行动作采样的选取,但该方法不是按照贪婪动作选取方式,而是根据不同概率选择适合的动作。

网络训练时,θ′当做每一次训练实例难度程度的评估标准,可看做是评价者的身份,通过贪婪动作选取方法,能够迅速得出正确的评估指标。而θ可视为执行者,即策略能力的评价。使用采样动作选取策略,能够预测出动作期望值,也就是执行者的决策的能力。实例策略网络与基准网络都是经过不同的动作选取恰当的动作,进而有效提升学习效率与模型性能。

模型训练结束后,按照贪婪动作选取策略,能够在最短时间内算出配送车辆路径,但会出现回路中线路交叉问题或者贪婪动作选取策略自负的行为,进而选取概率动作不是最大的概率动作。为了避免发生这两种问题,使用2-opt寻优方案,详细过程如下:

1)任意选取子回路γ上的两个点,同时将这两个点间的路径做翻转处理,进而生成新的子回路γ′;

2)假设γ′优于γ,就需要更新目前子回路γ=γ′,之后把迭代次数I重置,即次数设置为0,回到1),否则迭代系数设定为I=I+1,再回到1);

3)假设最大迭代次数依旧没有改进子回路,就需要通过2-opt全局寻找,并把γ当做最优子回路送回。

采样查找。该模型运用采样查找方式找出策略重复计算相同的实例,得到相同实例有多个解,选取当中最优的解。假设n描述采样的数量,则最优解计算过程如式(20)所示。

π′=arg min{L(π1),L(π2),…,L(πn)}

(20)

经过式(20)计算,可有效解决自负行为。由于本模型能够在最短时间内算出最优解,并能保证解的质量,进而有效保证农村物流配送路径成本最小。

3 实验数据分析与研究

3.1 实验环境

某乡县物流配送中心负责15个顾客点,有4台配送车辆,每台车装载量极限为6吨,每次配送路径最大距离为60m。物流配送中心空间坐标为(11.9km,19.9km),15个顾客空间坐标与需要配送货物情况如表1所示。

表1 顾客点空间坐标与需求情况

为了证实强化学习下最优配送路径规划效果良好,选取蚁群算法与多种群遗传算法作为对比方法,并求解配送最优路径,如图1-3所示。

图1 各方法下配送路径示意图

3.2 配送路径的距离对比分析

三种方法配送最优路径如图1所示。

通过图1可显著看出强化学习最优路径行驶最短,且没有出现重复路径,而蚁群算法与多种群遗传算法的路径距离较长,且存在重复路径。这是因为所提方法通过奖励函数与状态转移函数,不断调整配送车辆行驶状态,有效避免配送路径出现重复、交叉等问题。

3.3 配送车辆行驶成本对比

为了进一步证实强化学习方法的有效性,从物流配送中心历史数据库中,随机选取8次车辆行驶路径事件作为实验研究对象,以物流配送行驶成本与迭代计算次数作为评估指标对比分析,实验结果如图2、图3所示。

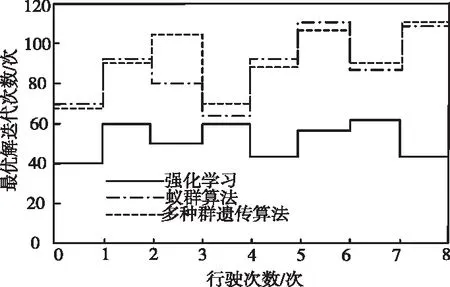
图3 算法迭代对比分析

从图2可知, 所提方法每次配送路径行驶的成本均小于对比方法, 因所提方法运用带有回滚基准求解策略的梯度, 并根据梯度下降更新策略网络,时刻调整配送路径策略,为此所提方法物流成本最小。

从图3可看出,所提方法找到最优解的最大迭代次数始终小于对比方法的迭代次数,且最大迭代次数小于60次,提高了配送效率。这是因为所提方法采用贪婪与采样两种全局搜索方式,能够有效提升最优解搜索的速度,为此在较少迭代次数就能找到最优解,证实所提方法方法性能良好。

4 结论

由于农村物流配送存在时效性差,运输成本高,为此,通过强化学习得到农村物流配送最优路径规划。以配送成本最小为目的,建立物流配送路径函数模型。采用奖励函数与状态转移函数设计策略网络,根据带有回滚基准训练策略网络。通过贪婪与采样计算得出配送路径的最优解,最终完成配送最优路径的规划。实验证实了所提方法能够有效降低物流运输成本,并能在迭代次数较低的情况下算出路径规划最优解。