连通域泛水填充融合k-means裂缝图像滤波算法
2023-09-20谢永华
谢永华,齐 杨
(1. 南京信息工程大学计算机与软件学院,江苏 南京 210044;2. 南京信息工程大学电子与信息工程学院,江苏 南京 210044)
1 引言
自21世纪初以来,我国的高速公路和隧道工程急剧增加[1],导致交通安全风险也随之提升,其中裂缝是影响公路和隧道安全的重要原因之一。同时由于裂缝产生环境,特别是隧道裂缝环境十分复杂,采集的裂缝图像除了包含本身需要识别的裂缝等病害之外,还包含各种噪声干扰,而且有些纹理特征与裂缝特征高度相似,在进行图像处理的时候很容易将两者混淆,提取的裂缝特征鲁棒性不高,从而导致后续识别率降低[2]。因此,对裂缝图像进行必要的滤波去噪处理就显得尤为重要。
目前裂缝图像滤波的方法主要有时间域和空间域两种算法,但这些算法各有各的优点和缺陷,Chunquan Dai等提出了采用改进的同态滤波算法对采集到的图像进行去雾和清晰处理,并采用自适应中值滤波对灰度图像进行去噪,有效降低了图像噪声,但裂缝细节出现了断裂和断点[3]。Mingfeng Lei等针对裂缝图像所包含的噪声类型不同,有针对性的将双边滤波和自适应中值滤波相结合,通过并行滤波得到最终去噪的图像[4],但裂缝细节边缘还是有一些模糊。Xiangyang Xu等研究了高斯滤波的最优参数,提出了一种基于信噪比梯度的高斯滤波算法,图像裂缝细节平滑效果明显[5],但仍有明显的噪声得到了保留。Lv, Yunlong等提出了一种基于小波变换的增强算法,首先使用小波变换对原图分解产生低频和高频信号,接着对低频信号进行同态滤波增强和直方图均衡化处理,对高频信号进行半软阈值函数去噪,虽产生的图像纹理细节清晰,但去噪效果一般[6]。张振海等采用了高斯-快速中值滤波算法来对图像进行滤波,可以去除大量噪声,但只能在一定范围内保护裂缝的边缘细节[7]。
综上可知,在裂纹图像滤除噪声方面,目前传统方法很难做到有效去噪同时且很好的保护图像细节,因此,本文提出了一种连通域的泛水填充和K-means融合的滤波算法,该算法先对裂缝图像进行预处理,作用于二值化裂缝图像上,去噪效果明显,而且保留了裂缝图像的细节特征,特别是解决了去噪后图像细节部分出现断裂和断点的现象,为后续裂缝特征训练和识别带来了有效性和可靠性。
2 连通域泛水填充和k-means融合滤波算法
2.1 二值化
为了使裂缝特征更加明显,首先对原始灰度图像进行阈值分割得到二值图像,图像阈值分割的方法根据图像中所要提取的目标与背景之间的差异性,通过合适的灰度阈值实现图像分割[8],即将某一个灰度值设为阈值,图像中大于这个阈值的设为255,小于这个阈值的设为0,如式(1)所示。
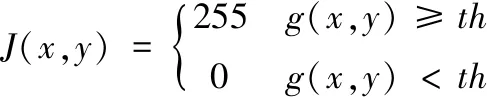
(1)
式中:th为设定的阈值,它的值是在0到255之间,J(x,y)为该点二值化后图像的灰度值。
选取阈值的方法有很多种,目前有双峰法,大津法和最大熵等,这里采用的是大津法(Otsu)[9]进行裂缝图像的二值化。
从图1中可以看出,二值化后的裂缝图像中噪点呈现点块状,而裂缝图像则为表现为一定的线性结构,因此可以对二值化后的裂缝图像进行连通域构造,方便后面对连通域的面积进行聚类分析,以达到去除噪声的目的。

图1 图像二值化
2.2 连通域面积的提取


(2)
式中:xi为第i个顶点的x轴坐标,yi同理,n为总顶点数目。
通过设定一个面积阈值T,将二值图像中小于这个面积阈值的连通域去除掉,则滤波后输出的图像可以表示为式(3)。
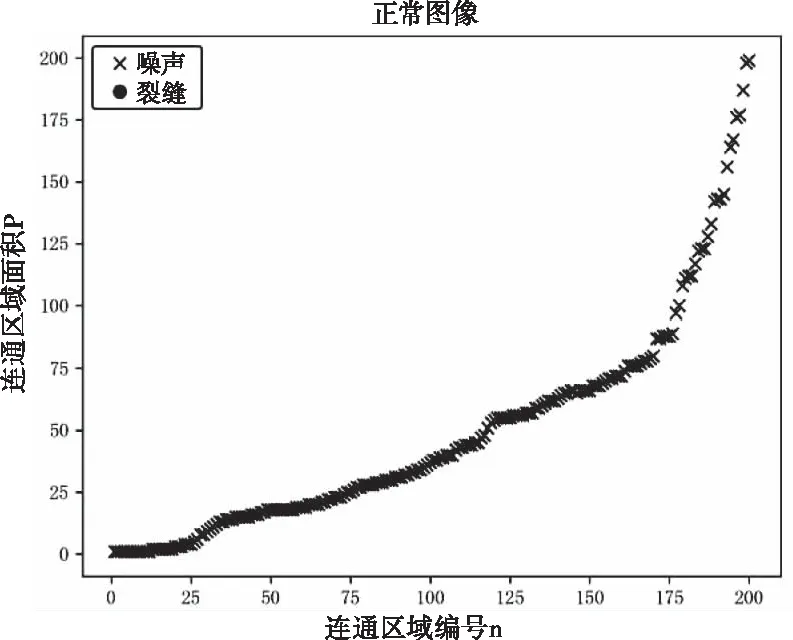
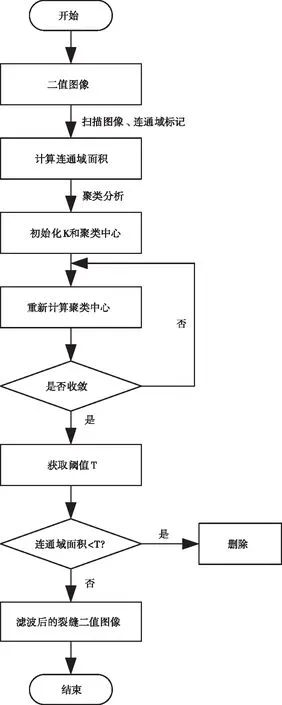
K(x,y)={Cj(x,y)∣Pj (3) 式中:Cj(x,y)为图像中第j个连通区域,n为连通域的个数。 阈值设置对滤波效果影响很大,手动阈值设置需不断的进行尝试。若阈值过小,滤波效果不理想,阈值过大,则会出现裂缝断裂,甚至整个裂缝都会当成噪声进行滤除。因此,需要根据连通域的分布,采用K-means算法对连通域的面积进行聚类分析计算自适应阈值。 K-means算法是一种运算简单、效果优良的无监督学习聚类分析算法,裂缝图像滤波的阈值计算可以看成聚类问题,根据连通域的特征值,把相似的对象规划到一类簇中,不相似的对象归到另一类簇中。它的算法原理如下: 假设样本数据为{x(1),x(2),x(3),…x(n)},从中随机选择k个数据作为初始聚类中心,如式(4)所示。 μ1,μ2,…,μk∈Rn (4) 则对于数据中的每个样本,计算它该属于的类,可采用的不同的距离度量方式,本文采用欧式距离,c(i)表示聚类结果,如式(5)所示 c(i):=minj‖x(i)-μ(j)‖2 (5) 然后按类别j,重新计算聚类中心,m为每个聚类中的个数,如式(6)所示 (6) 因为裂缝图像中仅存在两种类型连通区域,即裂缝连通区域和噪声连通区域,因此K-means聚类算法中的聚类个数就是2个,即K值为2,取一些裂缝图像计算其连通域面积特征,并将得出的700个一维数据集作为样本,k取值为2,随机选取样本两个值作为样本的初始中心,得出的聚类结果如下图2所示。 图2 连通域面积 由此可见,经过预处理后得到的图像,噪声面积大多数偏小,裂缝区域面积较大。进一步对预处理后包含裂缝和不包含裂缝正常图像进行聚类分析后可以发现,正常的裂缝图像连通域面积分布均匀,而含裂缝图像的连通域区域可以根据面积特征划分裂缝区域和噪声区域。如下图3和图4所示。 图3 含裂缝图像连通域面积对比图 图4 正常图像连通域面积对比图 在此基础上,基于K-means自适应阈值的具体步骤如下: 1)读取二值图像,计算并得到二值图像的面积值的一维矩阵; 2)随机选取一维矩阵的其中两个中心值,作为K-means聚类算法的初始点; 3)计算一维矩阵的每个点到中心点的距离,对中心值进行聚类分析并划分每个点; 4)重复2)和3)步骤,重新选取中心点,然后计算两个中心点的距离,一直到两者的中心点不再改变; 5)求得到的两个中心点的均值作为阈值,如式(7)所示 (7) 式(7)中,K1、K2分别表示噪声类和裂缝类的最终聚类中心。 在裂纹二值图像的基础上进行连通域填充,本文采用的方法是八邻域泛水填充算法。泛水填充算法涉及到三个参数的选择,分别是泛水填充算法的起始点,目标颜色如何判断以及替换的颜色。具体步骤如下: 1)选择初始的种子点 2)以初始种子点为中心,判断8邻域像素内种子点与初始点种子的差值,如果该差值小于设定的阈值,则将该像素点添加到种子点的区域内。如式(8)所示,p(x′,y′)为该区域内相邻的区域像素值,T为阈值。 |p(x′,y′)-p(x,y)|≤T (8) 3)反复进行2)的判断准则,以初始点为中心,如果满足2)的判断条件,用所选颜色替换掉当前颜色。 4)八邻域填充过程。像素间的连通性是确定区域的一个重要概念[11],8邻域是指点的垂直水平方向的四个相邻的像素点与其对角线上的点组合在一起,定义如式(9)所示。8邻域相比较4邻域更为全面、通用性更好,填充过程如图5所示,通过初始种子点的左、右、上、下、左上、左下、右上、右下八个邻域像素进行判断,然后再更新下一个像素点的连通区域,迭代往复。 N8=(x+1,y),(x-1,y),(x,y+1)∪ (x,y-1)(x+1,y+1),(x+1,y-1)∪ (x-1,y+1),(x-1,y-1) (9) 本文算法针对经过预处理后的二值图像,首先逐个扫描图像中的每个像素,对二值图像进行标识,获得每个连通域的面积,然后初始化图像聚类个数和聚类中心,使用K-means进行连通域面积的聚类分析得到自适应阈值,对连通域面积小于阈值的即判断为噪点并进行滤除,最后保存滤波处理后的裂缝二值图像。该方法将连通域泛水填充和K-means聚类相结合,不仅有效的去除了图像的噪声而且保留了裂缝细节特征。具体算法流程如图6所示。 图6 本文算法流程图 实验采用预处理后的道路和隧道裂缝二值图像,图7为横向、斜向、竖向、块状四个方向的代表性隧道和道路裂纹图像。实验是在硬件环境为:GPU是NVIDIA Quadro M4000, 主频2.10GHz,内存32G。采用20张(编号1-20)分辨率大小为226×328大小的裂缝图像进行滤波实验,软件使用的是Visual Studio 2017,基于OPENCV进行图像处理。 图7 隧道和道路代表性裂纹图像 为了得到滤波效果的客观评价,在此引入了图像滤波前后的峰值信噪比PSNR和均方差MSE[12],其PSNR和MSE的定义如式(10)和式(11)。 (10) (11) 式中,MAX为处理后目标图像中像素点的最大值,m、n为图像的长和宽,I(i,j)为处理后图像的灰度值,K(i,j)为处理前图像的灰度值。 图8和图9分别列出了4种隧道和道路裂缝类型代表图像的实验对比结果。从对比图可以看出均值滤波模糊了图像的细节,而中值、均值以及本文算法并没有使裂缝图像变得模糊。因为后续处理需要的就是裂缝的细节特征,所以此方法不适合裂缝图像滤波。中值滤波虽然没有模糊图像,但是从图中可以看出在隧道裂缝图像滤波的效果一般,在道路裂缝图像中由于噪声点细小滤波效果显得好一点,但是从细节中可以看出裂缝出现了断裂,如果增加核的大小裂缝断裂现象则会更加明显。高斯滤波是线性滤波器,能很好的保留图像的细节部分,但从对比实验中可以看出无论是在隧道裂缝图像还是在道路裂缝图像中滤波效果都很不理想。而本文算法是基于图像裂缝信息特征在空间分布上具有一定的连通性和连续性,噪点信息往往是孤立的且在空间上是不连续分布的,采用基于连通域的泛水填充方法,利用连通域的面积特征约束并对算法中的阈值实现自动获取进行噪声的滤除,一定程度上解决了手动调试阈值的缺点,提升了算法的效率。从实验结果对比图中可以看出在去噪方面能力更强,没有模糊图像,并且保留了裂缝图像的细节,这正与后续识别处理需要裂缝的细节特征相吻合,所以该方法相比较传统的滤波算法更加适合裂缝图像的滤波,效果显著。 图8 隧道图像滤波方法实验结果对比图 图9 道路图像滤波方法实验结果对比图 对隧道和道路裂缝原图及滤波后的图像分别计算PSNR和MSE 均值得到的结果如表1所示。由对比实验结果可以看出,本文算法滤波后的图像峰值信噪比值最大,均方差最小,而在图像方面,峰值信噪比PSNR越高,均方差MSE越小,说明图像的滤波效果越好。 表1 4种滤波算法处理后的PSNR和MSE均值对比 针对裂缝图像的滤波处理,提出了一种基于连通域的泛水填充和k-means融合的方法,首先对原图预处理后的增强图像进行阈值分割得到二值图像,再对其进行连通域标识,获得连通域的面积特征并进行聚类分析,最后将面积小于阈值的噪声点进行填充,保存滤波后的裂缝二值图像。实验表明,与传统的的滤波方法相比,本文算法对不同类型裂缝图像滤波效果明显,而且裂缝细节特征保留比较完整。2.3 基于K-means聚类分析的自适应阈值计算通域面积的提取
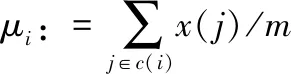



2.4 连通域泛水填充
3 算法流程
4 实验结果分析
4.1 实验条件



4.2 实验结果与分析



5 结 语
