风光储互补环境下电力发电机组散热器智能调度模型研究
2023-09-20孙頔
孙 頔
(北京科东电力控制系统有限责任公司,北京 100192)
发电机组的运行效率直接关系到能源利用效率和经济性。传统的散热器调度方法主要依赖于人工经验和定时控制,无法实现对发电机组实时状态的监测和调节。这种方式可能导致散热器过度或不足运行,影响发电机组的散热效果和运行效率。通过实时监测发电机组的温度、负荷等参数,结合智能算法和优化模型,可以实现对散热器的智能调节和优化控制,以最大限度地提高散热效果,减少能源浪费,提高发电机组的运行效率[1-2]。
以火电厂为研究对象,明确机组的约束,以风光水火电互补为前提,构建了一种优化调度模型。并通过优先顺序法和优化的布谷鸟算法对模型求解,实现最终调度[3]。提出电力机组联合负荷频率控制方法。分析发电机组的煤耗特性,建立经济目标函数,通过控制负荷频率获取机组最优出力系数[4]。基于此,提出一种考虑风光储互补的发电机组散热器出力智能调度方法。
1 散热器出力智能调度
1.1 调度模型
风光储互补能源是一种低碳环保的能源形式,有助于推动能源结构的优化和转型[5]。但是,风光储互补能源环境具有显著的波动性和不确定性,如风速、光照强度等因素都会影响机组发电,为发电机组散热器出力智能调度带来较大难度。为此,考虑风机发电和光伏发电,以最小发电成本和最小污染物排放惩罚成本作为目标,构建风光储互补环境下散热器智能调度模型。
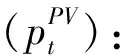
(1)
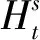
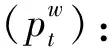
(2)
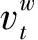

(3)

为确保电网系统的稳定运行,在考虑风光储互补的情况下展开发电机组散热器出力智能调度,需要给出对应的约束条件。
1)发电机组的散热器功率平衡约束
发电机组的生产和消耗是同步的,所以电网提供的电能和电网中的负载也是一致的,否则就会影响发电机组设备的稳定性以及安全性,对应的计算式:
(4)
式中:pL,t为发电机组的发电功率;pH,t为联合电力系统的输出功率;pPs,t为t时段内散热器出力的大小;pGi,t为第i组发电机组在t时段内发电机组的散热器出力情况;N为设备数量;i为常数。
发电机组的发电功率约束:
0≤pL,t≤pL,t,max
(5)
式中:pL,t,max为在t时段内发电机组的最大散热器出力值。
2)互补约束
为了有效避免电力系统运行中断,对发电机组散热器出力展开一定的限制[6],对应的计算式:
(6)
式中:pRe,t为联合系统在t时段内的散热器出力大小;pGi,max为设备在t时段内的最大散热器出力值。
基于以上约束条件,将最小发电机组发电成本和最小污染物排放惩罚成本作为目标函数[7-8],构建考虑风光储互补的发电机组散热器出力智能调度模型G(x):

式中:c(pGi,max)为散热器运行成本;f(pGi,max)为发电污染物排放惩罚成本;bi、αi和di分别为对应的散热器特性系数;ψ(i)为散热器耗电系数;T为时间。
1.2 模型求解
粒子群算法(PSO)[9-10]具有全局寻优能力和收敛速度快的特点,可以更好地优化发电机组散热器出力智能调度模型;PSO的操作步骤如图1所示。

图1 粒子群算法操作流程图
在PSO优化算法中[11-12],优化求解是一个动态的过程,对于惯性权重ω的处理主要通过迭代实现。由于采用线性递增惯性权重,并不能更好地反映实际寻优过程,同时也不利于寻找更好和更快的收敛结果。为了有效解决上述问题,采用自适应模糊推理求解惯性权重。
在模糊推理过程中[13-14],2个输入变量分别为发电机组发电成本和污染物排放惩罚成本,对二者展开线性变换,同时将其映射到[0,1]区间内,系统的输出为权重的变化率(),对应的计算式:
(8)
输入变量、惯性权重以及输出变量都具有3个模糊集,三者的模糊集合具有对应的隶属度函数。在实际应用过程中,需要通过输入的N和惯性权重,获取惯性权重的变化情况。
结合上述分析,将PSO[15-16]和模糊推理二者有效结合,进而提出一种基于模糊推理的粒子群算法并展开求解。
(1)PSO[17-18]初始化处理。在研究过程中涉及风能、太阳能以及发电机组,所以将维数设定为3,粒子数量设定为300,粒子的活动范围为不同发电机组实际运行下散热器出力的上下限,同时迭代次数设定为500;
(2)采用Rand函数将设定的300个粒子展开初始化处理,经过初始化处理后即可获取粒子起始位置和对应的起始速度;
(3)通过式(9)给出惩罚函数(F(x)):
(9)
式中:f(x)为目标函数值;β(k)为惩罚因子;zi(t)为复合函数;z(g(t))为对复合函数值的判断结果。
通过惩罚函数,求解粒子在不同时刻的目标值,确定粒子的局部和全局最优值;
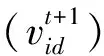

(5)惩罚函数法:采用惩罚函数法再次求解各个粒子在不同时段内的发电机组发电成本和污染物排放惩罚成本;
(6)判断最优及设定好的输出:判断全局最优以及迭代是否达到事先设定好的输出如果是,则直接输出最优发电机组散热器出力智能调度方案;反之,则返回步骤“(2)”。
2 结果与分析
2.1 智能调度方法的有效性
为了验证所提考虑风光储互补的发电机组散热器出力智能调度方法的有效性,将其与文献[3]方法与文献[4]方法作对比,实验在Matlab7.8环境下展开。为了验证各个方法的调度有效性,设定时间间隔为3 h,对比12 h内不同方法对散热器完成调度后发电机组的储/放电能功率改善效果。在考虑风光储互补的情况下,对电力发电机组设备储/放电能功率展开验证,实验测试结果如图2所示。
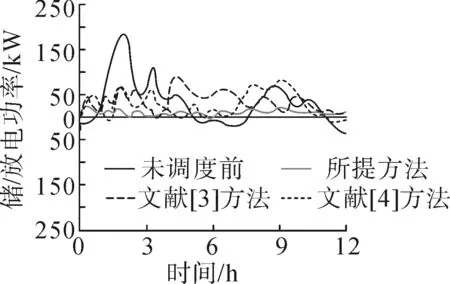
图2 发电机组储/放电能功率调度曲线结果
由图2可知,在考虑风光储互补的情况下,所提方法完成散热器调度后,系统的储电和放电功率都得到了比较明显的改善,且改善效果比较明显,不断趋近于0。文献[3]、文献[4]方法虽然系统的储电和放电功率也得到了改善,但获取的改善效果并没有所提方法好,波动性仍然比较大。由此可见,采用所提方法可以更好地实现发电机组散热器出力智能调度。
2.2 调度性能
为了进一步验证所提方法的调度性能,分析不同时段下各个方法对应的发电机组电力负荷变化调度情况,实验测试结果如图3所示。
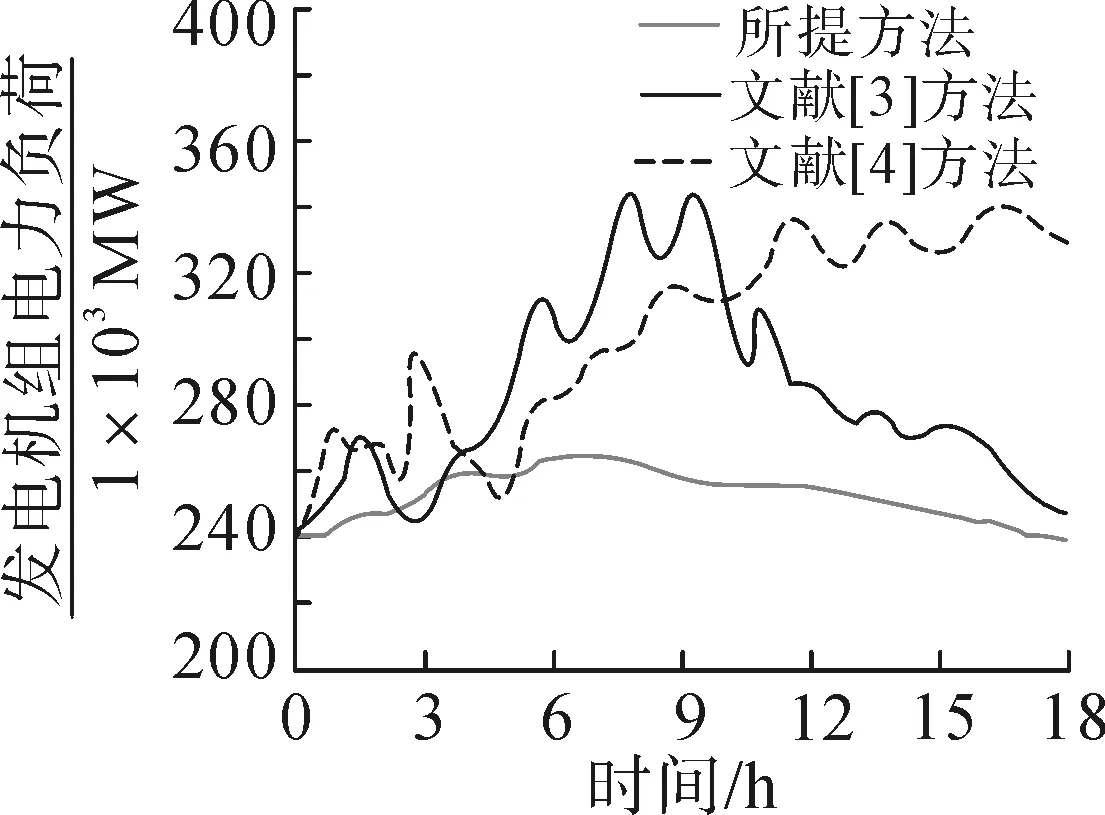
图3 发电机组电力负荷变化情况比较
由图3可知,经过不同方法调度处理后,所提方法的发电机组电力负荷曲线是3种方法中最低的,且曲线波动幅度小。其中,18 h时所提方法的电力负荷仅为240×103MW,而文献[3]方法、文献[4]方法的发电机组电力负荷值均大于所提方法,且负荷曲线波动较大。这说明所提方法对发电机组散热器完成调度后,发电稳定性得以优化。
2.3 方法的有效性
为了进一步验证所提方法有效性,选取5种测试对象,实验次数设置为60次,分析经过调度处理后各个方法的发电机组耗油率变化情况,实验测试结果如图4所示。
由图4可知,利用所提方法调度后,所提方法获取的发电机组耗油量取值明显低于文献[3]、文献[4]方法,最高耗油仅为50 g/(kW·h);而其他2种方法均在100 g/(kW·h)以上,充分验证了所提方法的优越性。
2.4 耗时比较
选取需调度散热器目标数量为500个,以时间为实验指标,分析各个方法对不同数量的发电机组展开调度所花费的时间,结果如表1所示。
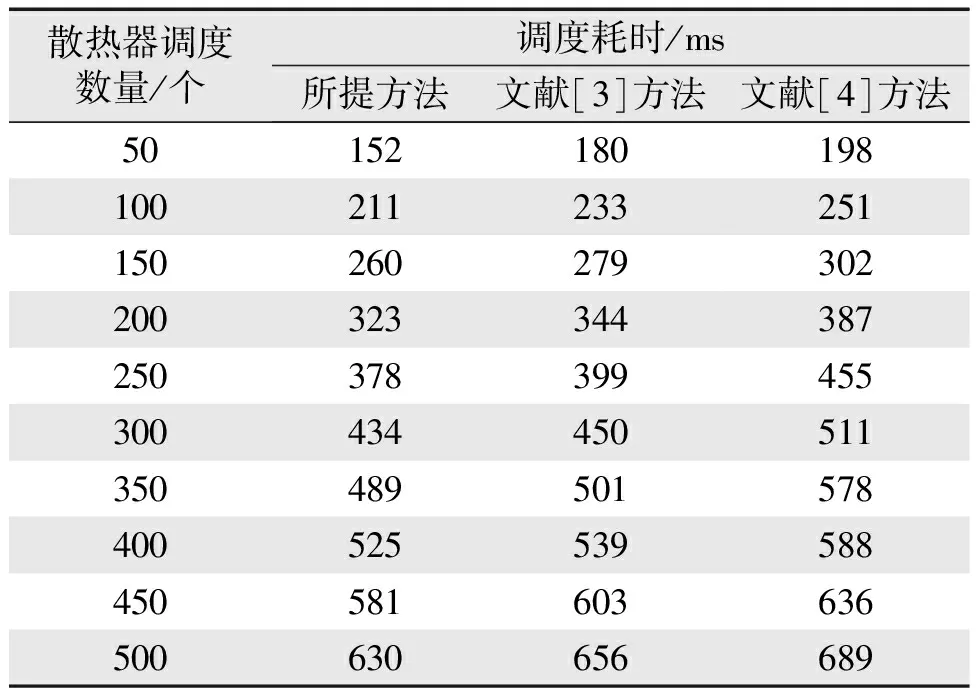
表1 耗时对比测试结果Tab.1 Time comparision test results
由表1可知,所提方法与另外2种调度方法相比,在调度目标数量相同的情况下,采用所提方法可以以更快的速度完成任务,耗费的平均时间最少,在目标数量500个时,耗时仅为630 ms;而文献[3]、文献[4]方法的耗时则大于650 ms。这说明所提方法可以有效减少发电机组散热器出力智能调度时间。
2.5 散热器智能调度效果
为进一步测试研究提出的散热器智能调度效果,本实验以发电机组实时温度为指标,设定实验风光互补发电环境中参与测试发电机组有:功率为100 kW、效率为18%、总容量为400 kW的光伏发电机组,额定功率为200 kW、起动风速为3 m/s、切入风速为4 m/s、切出风速为25 m/s的风力发电机组以及容量为300 kW的备用燃气发电机组。以上发电机组均具备快速启动和停机的能力。利用研究方法对散热器完成智能调度,在每台发电机组的发热区安装Fluke 62 MAX+便携式红外线测温,实时测量其温度(发电机组所处室内环境温度为22 ℃),研究方法应用前后的发电机组温度具体数据如图5所示。
由图5可知,光伏发电机组正常运行时温度为40 ℃,风力发电机组正常运行时温度为60 ℃,备用燃气发电机组正常运行时温度高达85 ℃。应用研究方法对散热器完成智能调度后,3种发电机组的温度均得以降低,光伏发电机组和风力发电机组的温度分别降低了28、40 ℃,备用燃气发电机组温度降低了30 ℃。这说明散热器智能调度方法,可有效地改善了发电机组的散热效果。通过合理调度散热器的使用时间,可以更好地控制发电机组的温度、优化发电效率。
3 结语
本研究提出的发电机组散热器出力智能调度方法,可以有效减少散热器出力智能调度时间和发电机组的耗油率,降低发电机组运行时的温度。但是,由于研究时间有限,所提方法仍然存在一定的不足,后续将对其展开进一步优化和完善,使其可以得到更加广泛的应用。
