随机供水条件下机压微灌干管管网优化设计研究
2023-09-19马朋辉苏晓飞王净刘怀宇林平
马朋辉 苏晓飞 王净 刘怀宇 林平







关键词:微灌干管管网;随机供水;遗传算法;同步优化
管道输水灌溉就是利用管道将水直接送到田间进行灌溉,以减少水在明渠输送过程中的渗漏和蒸发损失,具有最大限度节约水资源、减少占用耕地、降低能耗、高效输水等特点,已成为节水灌溉的主要措施之一,在我国平原井灌区、渠灌区和提水灌区得到广泛应用[1]。但管道输水灌溉系统投资相对较高,国内外学者开展了大量的研究以降低管道灌溉系统工程投资。
灌溉管网优化主要包括布置优化及管径优化两个方面。布置优化主要是进行管网线路选择优化,是管径优化的前提和基础,灌溉管网中管道总长度及工程投资直接受管网布置形式的影响。正交表法[2]、最小生成树法[3]、遗传算法[4-6]、列队竞争算法[7]、蚁群算法[8]、混合启发式算法[9]等被用于灌溉管网的布置优化研究。管径优化是确定管网中各级各管道的直径以在满足各需水节点压力、管道流速等要求的条件下使得系统投资最小。传统的蚁群算法[8]、动态规划法[10]、线性规划法[11]、非线性规划法[12]以及人工神经网络[13]、遗传算法[14-15]等近年来广泛应用的新型智能算法被用于管径优化研究。
以上研究均是在灌溉管网中各需水节点的位置及流量已定的条件下开展管网布置优化研究,或是在布置已定的情况下开展管径组合优化研究,关于灌溉管网布置形式与管径组合同步优化的研究较少,且以往研究多为续灌或轮灌条件下灌溉管网的布置优化或管径优化,未开展随机供水条件下灌溉管网的布置形式与管径组合同步优化的研究。为实现随机供水条件下灌溉管网布置形式和管径组合的同步优化,本文建立了随机供水条件下灌溉管网布置与管径同步优化的数学模型,并给出基于遗传算法的模型求解方法,以期为相关工程优化设计提供实践参考。
1 管网优化数学模型
微灌管网系统主要由加压泵站、输水管、干管、分干管、支管、毛管、控制与保护设备等组成,其中输水管、干管及分干管组成干管管网。典型微灌管网系统示意见图1。
笔者已经提出了不限定灌溉面积情况下灌水小区布置与管径的同步优化方法[16],本研究主要开展微灌干管管网的优化设计。与输配水、供水等树状管网主要选择能够连通所有需水节点管网连线方案的布置优化不同,微灌干管管网的布置优化主要涉及微灌干管管网的控制灌溉面积、干管和分干管的管段长度及段数。基于分级优化的思路,通过文献[16]可以确定灌水小区的布置形式,并得到灌水小区长度和宽度的优化结果,即微灌干管管网中干管、分干管的管段长度已经确定,则微灌干管管网布置优化主要是确定干管及分干管的段数,管径优化主要是确定输水管、干管、分干管等各管段的管径及水泵扬程。
微灌干管管网优化的主要目的是选择合适的管网布置形式、各管段的管径及水泵扬程,使单位面积年费用最低。单位面积年费用主要由水泵年动力费及管网投资年费用组成,且两部分成负相关关系。若选择的水泵扬程大则年动力费用高,但可以选择较小的管径以降低管网投资;若选择的水泵扬程小则年动力费低,为满足各需水节点的压力须选择较大的管径以减小沿程水头损失,则管网投资高。本研究以文献[16]中的优化结果为基础,以微灌干管管网单位面积年费用最低为目标函数,考虑节点压力水头约束、管径约束、流速约束等约束条件,从干管管网中只有一个灌水小区到干管、分干管方向各有多个灌水小区进行优化,进而确定干管管网中干管及分干管的管段数、各管段管径、水泵扬程及干管管网的控制面积。
1.1 目标函数
微灌干管管网单位面积年动力费、年运行维护费及输水管、干管、分干管、电磁阀等固定投资年费用之和最小,即
式中:F为单位面积年综合费用;Fa为单位面积年固定投资;Fe为单位面积年动力费用;Fo为单位面积年运行维护费用;Cp为单座泵站投资,根据文献[17]中的方法计算;Cd为输水管投資;Cg为干管投资;Cs为分干管投资;Cv为电磁阀投资;A为微灌干管管网控制灌溉面积;a为资金回收系数;r为年利率;t为资金回收年限;Ck为输水管选择k号标准管径所对应的单价;Ld为输水管长度;Cik为干管第i管段选择k号标准管径所对应的单价;Lg为干管管段长度;Cijk为第i条分干管第j管段选择k号标准管径所对应的单价;Ls为分干管长度;N为干管管网中分干管的数量;M为单条分干管上支管的数量;M0为单条分干管的管段数,依单条分干管上的支管数量而定,支管数量为单数、双数对应的M0分别为M-1和M;E为电价;T为微灌系统年工作时长;Q为微灌系统流量;H为水泵扬程;η为水泵效率。
1.2 约束条件
1)压力约束。微灌干管管网中各节点的压力水头应满足灌水小区进口压力需求,且各管段的压力应在管材承压范围内,即
式中:Hin为管网中各节点所需压力水头;Hk为管网中节点的压力水头;Hc为管材承压能力;hb为水泵首部水头损失;Ig为干管方向地形坡度;Is为分干管方向地形坡度;Li为第i段干管长度;Lj为第j段分干管长度;k1为从干管管网入口至某一节点所经过的干管段数;k2为从干管管网入口至某一节点所经过的分干管段数;hw,i为从管网入口至某一节点的总水头损失;α为局部水头损失加大系数,取值为1.05;f为管材摩阻系数;Qi为管段流量;Di为管段直径;m为流量指数;b为管径指数;p为干管管网中各需水节点(灌水小区)平均运行概率;nh为某一管段下游需水节点的数量;qi为某一需水节点的流量;U为正态分布的百分位数,与确定的运行质量相关;Tf为微灌干管管网控制范围内地块的灌水延续时间;Nh为微灌干管管网控制范围内灌水小区的数量;I为灌水周期;Tx为微灌系统日运行时间。
2)管径约束。顺水流方向,前一管段所选的标准管径Di应不小于后一管段所选的标准管径Di+1:
2 基于遗传算法的模型求解方法
遗传算法是一种模拟生物界自然选择和遗传机制的全局随机搜索智能优化算法。将优化问题的解比作物种中的个体,针对优化问题初步拟定的多个可能解所构成的组合比作物种的初始种群,遗传算法在计算过程中模拟自然界中物种的进化,初始种群通过选择操作做到优胜劣汰、适者生存,通过交叉操作保证种群的稳定性以使其朝着最优解的方向进化,通过变异操作保证种群的多样性以避免交叉可能产生的局部收敛,并通过设计的适应度函数选择产生质量更优的新一代种群,在产生的每一代种群中保留一组候选解,如此不断进行遗传操作,直至满足预先设定的算法终止条件,得出所求解问题的最优解或近似最优解。
基于遗传算法的模型求解流程如下:
1)随机产生初始种群。初始种群中个体所包含的决策变量为各管段管径及水泵扬程。本文均采用标准管径,将管径由小到大排序并进行编号,采用以序号代替标准管径的整数编码方式;水泵扬程采用以实际值编码的实数编码方式。
2)水力计算。确定管网中各管段的流量并计算管网水头损失及各节点的压力水头。针对本文研究的随机供水管网,采用Clément方法[6]确定每一管段的设计流量后进行管网水力计算。
3)计算个体适应度。前述构建的随机供水条件下微灌干管管网优化数学模型带有约束条件,须对约束条件进行处理使其转化为无约束优化问题,本文采用罚函数法实现上述转化。罚函数法不需要提供初始可行解,当解在不可行域内时增加惩罚项使其远离最优解。采用罚函数法构建的适应度函数为
4)遗传操作。基于计算的群体中每个个体适应度值,采取随机遍历抽样方法从当前种群中选取一定比例的个体作为父辈繁殖子代;从第一行开始将选取的父辈种群中的相邻两行进行交叉操作并以一定概率选择变异的基因位并在该位基因所允许的范围内进行随机变异操作。经遗传操作产生新一代种群后对该种群中所有个体进行解码,重复步骤2)、3),分别对其进行水力计算并计算个体适应度值。
5)判断是否达到算法终止条件。判断是否达到算法预先设定的终止条件,若达到了则终止计算并输出最优解;若未达到则重复步骤4)的操作。
3 应用
3.1 基本数据
某项目区种植作物为夏玉米,中等干旱年充分灌溉净灌溉定额为2100m3/hm2,目前采用渠道输水、地面灌溉的方式,为推进灌区深度节水,现拟将地面灌改为滴灌。土壤质地为中壤土,初始含水率为10%,土壤容重为1.42g/cm3,计划湿润层深度0.70m,设计土壤湿润比为70%,田间持水率为25%,适宜土壤含水率上、下限(质量百分比)分别为田间持水率的90%、60%,设计耗水强度为6.8mm/d;毛管间距为1.0m,灌水器间距为0.5m,支管和毛管方向的地面坡度均为1/200,选用的毛管外径为18mm、单价为1.95元/m;灌水器的流量指数、流态指数、制造偏差系数、设计允许流量偏差率分别为0.604、0.520、0.030、0.200,灌水器最小、最大工作水头分别为5、13m,该微灌系统灌溉水利用系数为0.95;年利率为7%,微灌灌水小区、干管管网的折旧年限分别为8、20a,年平均维修费率为5%,水泵运行效率为0.65,电价为0.6元/(kW·h),底阀、首部枢纽及吸水管水头损失之和为7m,输水管长度为30m,电磁阀的价格为600元/个。微灌干管管网所用UPVC管材的单价见表1。
3.2 控制参数选取
遗传算法中控制参数的选取对计算结果精度有一定影响,其中影响较大的是种群规模及最大遗传代数,即(种群规模,最大遗传代数),选取(200,50)、(200,100)、(200,200)、(200,500)、(50,500)、(100,500)共6种参数组合对计算结果的精度进行分析,当取(200,500)组合时精度较高,以此组合确定种群规模及最大遗传代数取值,其余参数均按一般取值。
基本遗传算法中的具体参数为:种群規模为200,最大遗传代数为500,交叉概率为0.9,变异概率为1/NVAR(NVAR为模型中变量个数),代沟为0.9,初始温度为0.00001,温度冷却系数为0.99。
3.3 优化结果分析
根据文献[16]提出的以控制面积最大为目标的毛管双向布置灌水小区优化数学模型及求解方法,得出灌水小区的优化结果见表2。
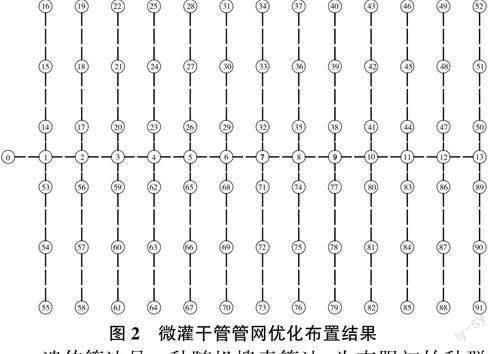
把灌水小区的优化结果作为相关输入参数进行随机供水条件下微灌干管管网的优化,管段流量确定过程中假设微灌干管管网的运行可靠度为99%,根据文献[6],正态分布函数的百分位数为2.324,具体优化结果见表3、表4及图2。
遗传算法是一种随机搜索算法,为克服初始种群在产生、交叉、变异等过程中的随机因素对算法求解性能的干扰,将基于遗传算法的管网优化程序独立运行100次,从100次优化结果中选择单位面积年费用最低的为最优解,并比较每次优化结果与最优解的相对偏差,结果见表5。
本文管网优化程序100次的独立运行结果中,最优解为964.24元/(hm2·a),其中相对偏差小于5%的概率为45%、相对偏差小于8%的概率为73%、相对偏差小于10%的概率为98%,说明算法收敛性强,具有较高的计算精度,能够满足实际生产需求。
4 结论
在不限定面积的情况下,以微灌干管管网单位面积年费用最低为目标函数,考虑节点压力水头、管径、流速等约束条件,建立了随机供水条件下微灌干管管网布置与管径同步优化数学模型,并给出了基于遗传算法的模型求解方法。
实例计算结果表明,以控制面积最大为目标的毛管双向布置灌水小区优化模型优化结果为基础进行微灌干管管网优化时,得到的干管管网控制面积为93.40hm2,单位面积年费用为964.24元/(hm2·a)。通过对程序多次独立运行所得优化结果与最优解相对偏差的分析表明,本文所提出的基于遗传算法的模型求解方法具有较高的计算精度,能够满足实际生产需求。
采用基于整数和实数的混合编码方式,所得到的管径为标准商用管径,避免二次调整管径使结果偏离最优解,适用于地形平坦、水源有保证且不限定单个微灌系统控制面积情况下随机供水微灌干管管网的优化。
