计及光伏和电动汽车的多阶段配电网拓展规划

2023-09-19陈坤孙开元林琳王梦郑杰辉李志刚

电气传动 2023年9期

陈坤，孙开元，林琳，王梦，郑杰辉，李志刚

（1.广东电网有限责任公司广州供电局，广东广州 510620；2.华南理工大学电力学院，广东广州 510641）

近年来，随着可再生能源、电力电子设备的高比例接入以及终端电气化率的快速提升，越来越多的新能源不断接入电网[1-3]。同时，在“碳达峰”、“碳中和”等能源理念下，多元化规划元素（光伏、电动汽车）大量接入城市电力系统，导致电网结构日益复杂化[4-5]。大型城市电网负荷高速增长且电网建设难度不断增大，急切需要对现有的配电网网络进行拓展规划。

目前，国内外对于配电网的拓展规划已有较多研究，根据规划模型可以分为两类：直流配电网模型和交流配电网模型。直流配电网模型由Haffner 等人在文献[6-7]中首次提出，用基尔霍夫定律以及配电网规划约束构造了具有广泛适用性和灵活性的多级优化模型。文献[8]比较了近似直流网络模型和全交流潮流模型在最后一个规划阶段的支路电流、变电站注入以及节点电压值误差，结果验证了近似网络模型的准确性。尽管这种直流建模具有一定的局限性，但基于线性化配电网拓展规划模型所产生的误差对于长期是可以接受的。

作为分布式新能源的一种重要形式，光伏发电有着良好的发展前景，将分布式光伏的接入与配置纳入城市配电网规划已成为必然趋势[9-10]。文献[11]考虑光伏输出特性造成的配电网潮流方向改变和电压偏差等影响因素，提出了一种考虑不同光伏渗透率和电网运行风险的配电网规划方法。文献[12]计及光伏之间、光伏与负荷之间的相关性，并考虑负荷概率分布参数时序差异性，建立了联合运行优化的长短期规划模型。在配电网的长期规划中，光伏电站的可投建的数量和容量都具有一定的可调整性，在规划前期需要结合负荷需求进行相应的部署。上述相关的研究工作侧重于解决光伏并网的电压与可靠性分析问题，没有将光伏的定容选址纳入配电网的总体规划。

而未来随着电动汽车大规模接入电网充电，需要在配电网中增加大量的充电站以及电力供应，将改变配电网的负荷结构和特性，对配电网的运行与规划产生不可忽视的影响[13-14]。综合考虑电动汽车充电站规划和配电网接纳能力的协同发展具有重要意义。文献[15]以建设运营总成本最小为目标，评估配电网对候选接入方案的接纳能力，从而建立了充电设施规划模型。文献[16]综合考虑投资运营成本和可再生能源利用率，提出多能源复合电动汽车充电站的功率分配方案。文献[17]针对分布式电源同时为配电网负荷和充电站供电的情况，建立了考虑电动汽车特性的定容选址模型。文献[18]针对光伏电源出力与充电站负荷的随机性分布，采用蝙蝠算法对两层级中心选址模型进行全局寻优。含光伏分布式电源和电动汽车充电站的配电网规划问题都具有投建点的不确定性，如何协调与平衡好两者与配电网的节点负荷是一大难点。目前综合考虑分布式光伏与电动汽车充电站的联合选址规划问题的相关研究较少，没有直观地体现两者的协同规划给配电网带来的效益。因此，提出一种计及光伏和电动汽车的配电网多阶段联合规划方法。

在上述背景下，本文考虑分布式光伏的并网消纳和电动汽车的灵活接入，针对不同规划阶段的负荷需求情况将负载曲线离散化为三个负荷水平等级，并分别描述峰平谷时段用电量；然后，引入电动汽车充电站充放电价格特性，建立了以投资—运行—收益综合成本最优为目标的联合配电网双层拓展规划模型，采用Gurobi 求解器对线性化之后的混合整数线性规划问题进行求解，给出了相应的线路投建规划方案及规划成本费用，以此实现配电网的可再生能源并网消纳。

1 基础模型

1.1 模型假设

计及光伏和电动汽车的配电网联合规划方案如图1 所示。一般来说，对配电网进行拓展规划需要考虑完整的交流模型，但完整的交流模型在优化求解上十分复杂，需要通过启发式算法或二阶锥松弛简化模型来求解[19]。因此本文采用了改进的直流模型，该基础模型的合理性与有效性已在文献[20]中得到验证，其结果均表明使用该直流模型得到的结果与交流模型之间的平均误差能够控制在1% 以下，属于长期规划的可接受误差范围。因此本文引入了一个改进的网络拓展规划模型并做出如下假设：1）各节点电压仅在基准值附近微小变化；2）各支路电流和节点功率具有相同的功率因数；3）将负荷表示为恒定的注入电流。

图1 计及光伏和电动汽车的配电网联合规划方案Fig.1 The joint distribution network planning considering PV and EV

1.2 光伏模型

光伏发电的输出功率与光照强度、环境温度等密切相关，其函数关系式可描述为

式中：Ptpv为t时刻的光伏实际输出功率；Htac为实际的太阳光照强度；Pstc为STC（标准测试条件）下光伏组件的最大输出功率；Kpv为功率温度系数；为电池板工作温度；Tr为参考温度；Gstc为STC（标准测试条件）下的太阳光照强度。

1.3 电动汽车充电站模型

以投资运营总成本最小为目标，本文主要从电网的投资效益出发，暂未考虑用户的充电习惯以及行车里程等。总成本表达式为

式中：α为年度通胀调整利率；分别为充电站的投资成本、运行成本、保养维护成本以及运营收益。

的表达式为

式中：t∈T为时间集合；ev∈EV为电动汽车充电站集合；i∈ΨEV为电动汽车充电站节点集合；csellt，cbuyt分别为充电站的单位售电价格和单位购电价格；ηcharge为充电站的输入效率；Pevi为第i个充电站节点的容量。

配电网规划区域内的所有充电站节点的总容量需要满足该区域内的所有充电需求之和，表达式为

式中：为整个配电网区域内所有充电需求。

电动汽车充电负荷的比例应在整体配网负荷中合理分配，表达式为

式中：ll∈LL为负荷水平集合；为负荷水平ll下第i个充电站节点的容量；λ为电动汽车充电负荷占节点总负荷需求的最大比例；μll为负荷水平ll下的负荷系数；LDit,ll为节点i的负荷需求量。

2 配电网拓展规划模型

本文提出的改进配电网拓展规划模型存在以下几点假设条件：1）以年为单位，引入研究常用的辐射状分布网络拓展规划模型，分多个阶段逐步扩建；2）在中长期的配电网拓展规划中，通常采用负荷水平来近似地描述负载曲线；3）拓展规划包括变电站的新建、线路的新增、光伏电站和电动汽车充电站的新建等。

2.1 目标函数

本文考虑以配电网扩展规划总成本净现值最小化为目标，包括投资成本净现值IPV、生产成本净现值PPV、维护成本净现值MPV、网络损耗净现值OPV以及甩负荷成本净现值LSPV。总成本净现值表达式为

其中

式中：l∈L={EFB,ERB,NAB,NRB}为支路集合，分别表示{现有不可替换分支，现有可替换分支，新建增加分支，新建替换分支}；tr∈TR={ET,NT}为变压器集合，分别表示{现有变压器，新增变压器}；i∈{ΨLN,ΨSS,ΨPV,ΨEV}为节点集合，分别表示{负荷节点，变电站节点，光伏电站节点，电动汽车充电站节点}；pv∈PV为光伏电站集合；k∈{Kl,KTR,KPV} 为投资选择集合；ll∈LL={LL1,LL2,LL3}为负荷水平集合；为0-1变量，表示在配电网扩展规划的阶段t下，支路lij的投资决策，xlijkt= 1 表示在t阶段选择投资建设支路lij，否则不进行投资建设；，为0-1 变量，表示在阶段t下变压器tr和光伏电站pv的投资决策，其含义与支路同理；为0-1变量，表示在阶段t下，支路lij和lji的投用决定，之所以要用两个变量表示，是因为每条支路可以有两个代表方向，= 1表示在t阶段选择投入使用支路lij，否则不进行投入使用；，为0-1 变量，表示在阶段t下，变压器和光伏电站的投用决定，其含义与支路同理为支路电流的幅值与方向，需要注意的是，当lij中有从节点i到节点j的电流流过时为1为正值，和都为0，当lij中没有电流流过时和均为0；为在阶段t负荷水平ll下，变电站i的变压器tr的注入电流值；为在阶段t负荷水平ll下，由节点i功率不平衡引起的甩负荷量；CIk，CMk分别为投资成本系数和维护成本系数；RATEll，DURLll分别为负荷等级ll下的电费和每日持续时长小时数；VOLL为单位甩负荷成本；RRl，RRtr，RRpv分别为支路、变压器、光伏的资金回收率；Rlk为选择k的支路l的电阻值；Rtkr为选择k的变压器tr的电阻值。

2.2 约束条件

2.2.1 配电网平衡约束

一般来说，配电网拓展规划常使用基尔霍夫电流定律和基尔霍夫电压定律来对直流模型进行分析，作为该配电网节点平衡约束，对各个节点的注入电流、流出电流和负荷需求进行建模：

2.2.2 电网安全运行约束

配电网的节点电压、线路电流、变电站和光伏电站的注入功率以及节点甩负荷量均需满足一定的上、下限约束。

2.2.3 投资和投用约束

在整个配电网规划过程中，每个元件或设备（线路、变压器和光伏）最多仅能经历一次调整（新建、替换、扩容）：

在新建线路或变压器时，需要考虑线路的投资建设必须在投入使用之前进行，并且若有线路被替换，则原有线路投用变量为0，若没有进行替换，则为1。

式中：，为在阶段t下，现有可替换分支lij和lji的投用决定；为在第一阶段下，新建替换分支lij的投资决策；k'∈KNRB为新建替换分支集合。

线路的电流方向有且只有一个：

2.2.4 网络约束

配电网在规划运行中，必须满足径向辐射状分布，即不能形成环状。通过确保有负荷需求的节点有电流流入，而其余节点最多有一个输入电流，即可保证潮流的单向性：

式中：i∈Ψlj为该配电网的所有节点集合。

3 算例分析

将所提出的配电网多阶段拓展规划模型应用于一个虚拟改进24 节点网络中，该网络由20个负荷节点、4 个变电站节点以及32 条支路构成，具体的拓扑结构如图2 所示。从图2 可知，21和22节点上已有变电站，变电站内部各包括一台变压器，2—21 和6—22 为固定不可替换支路，1—21和8—22为可替换支路。

图2 24节点配电网系统拓扑结构图Fig.2 24-node topology diagram of distribution network system

3.1 参数设置

基本情景设定如下：

1）整个配电网络的基准值为1 MV·A和20 kV，节点电压上、下限分别为21 kV 和19 kV。本次规划分为3 个阶段，每1 a 作为1 个阶段，年通货膨胀调整利率为10%，支路的资本回收率为11%，变压器的资本回收率为13%，线路阻抗为0.732 Ω/km，甩负荷成本设为2 000 k＄/（MW·h）。

2）在规划过程中，新建的变电站、线路、光伏电站以及电动汽车充电站的参数如表1 和表2 所示。电动汽车充电负荷占总负荷的5%以上，充电费用设为当前电网电价的1.5倍。

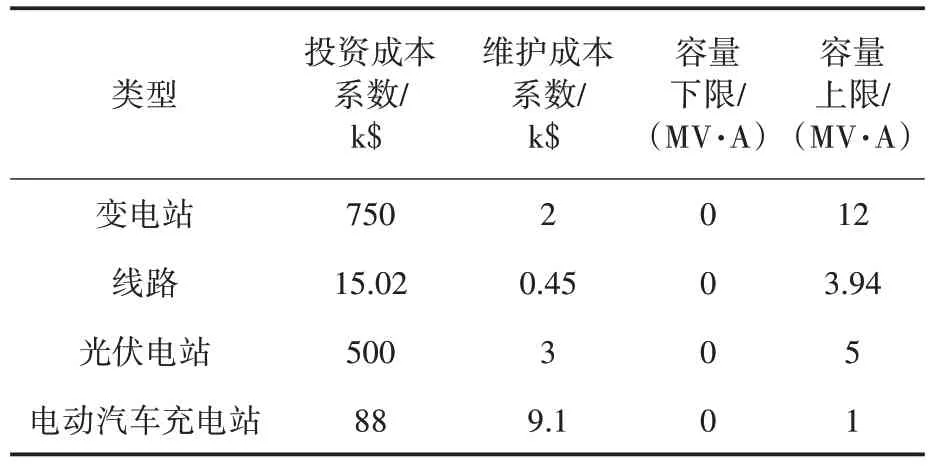
表1 新建设备参数Tab.1 The parameters of new equipment

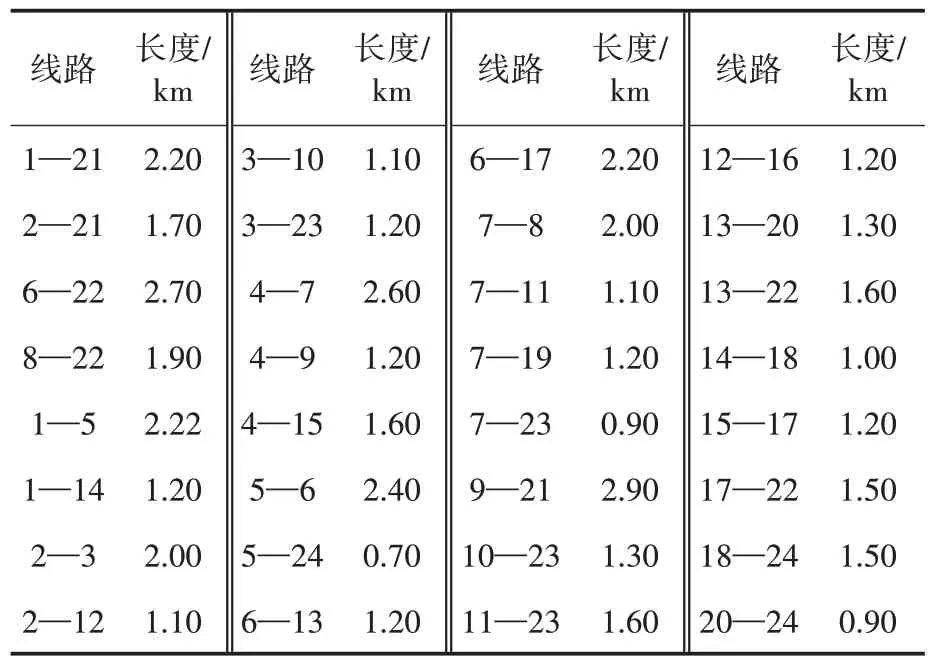
表2 线路参数Tab.2 The parameter of lines

3）本文将负载曲线离散化为3个负荷水平等级LL1，LL2和LL3，分别描述负荷节点在峰时段、平时段和谷时段的每小时最高用电量，日持续小时分别为6 h，10 h和8 h。

3.2 场景分析

为了验证和分析光伏和电动汽车对配电网拓展规划的影响，设置4种场景进行比较分析：

场景Ⅰ：不考虑光伏和电动汽车的拓展规划；

场景Ⅱ：只考虑光伏接入的配电网拓展规划；

场景Ⅲ：只考虑电动汽车充电站的拓展规划；

场景Ⅳ：综合考虑光伏以及电动汽车的拓展规划。

3.3 规划结果

场景Ⅰ的规划结果将作为评估光伏和电动汽车对配电网规划影响的基准值，规划结果如表3所示，规划拓扑图如图3～图6所示。

表3 24节点网络规划成本Tab.3 The planning cost for the 24-node network

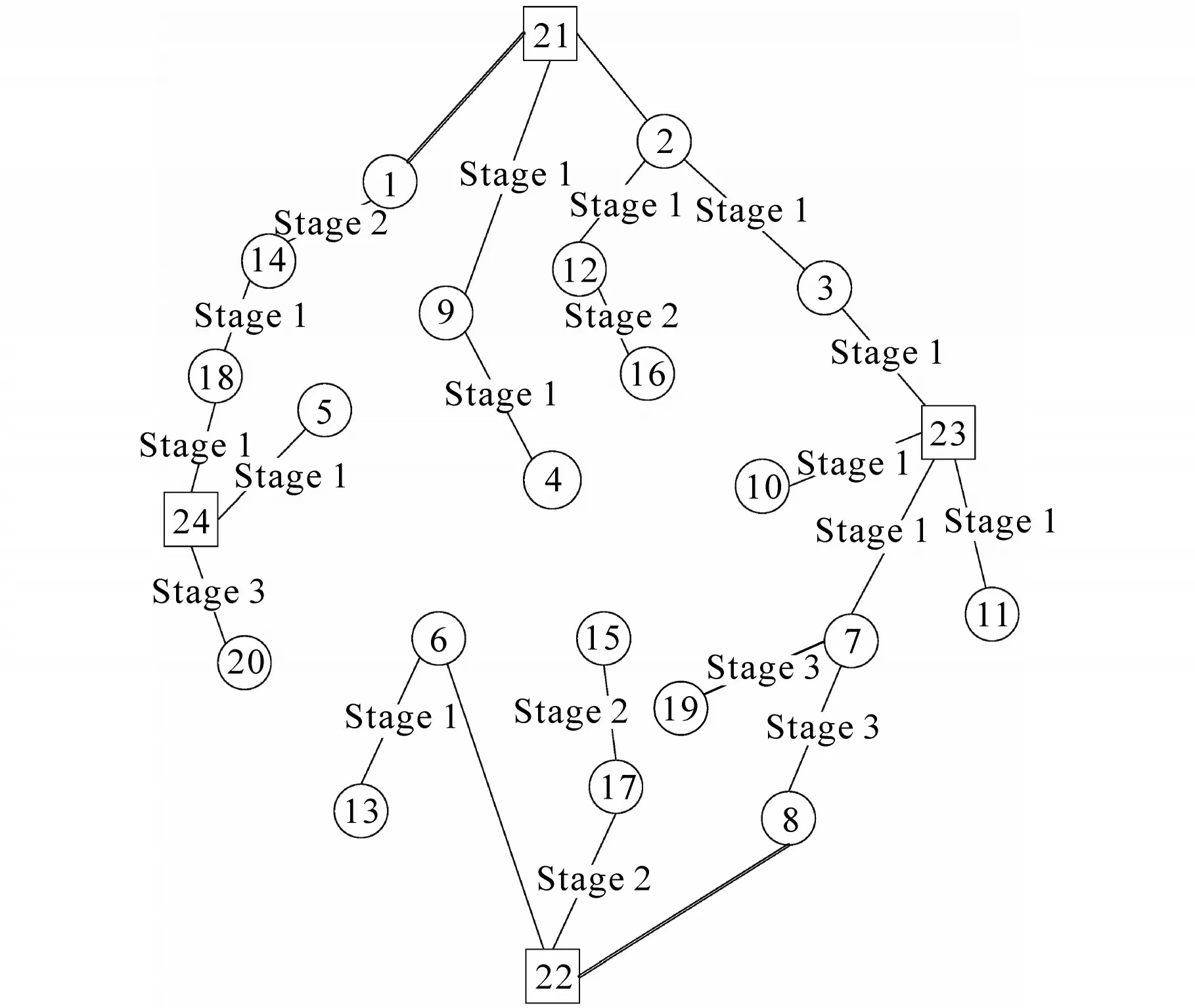
图3 不考虑光伏和电动汽车的三阶段规划拓扑图Fig.3 The three-stage planning topology without PV or EV

图4 只考虑光伏的三阶段规划拓扑图Fig.4 The three-stage planning topology with PV

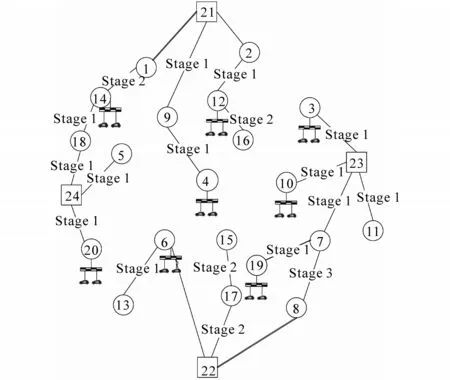
图5 只考虑电动汽车的三阶段规划拓扑图Fig.5 The three-stage planning topology with EV

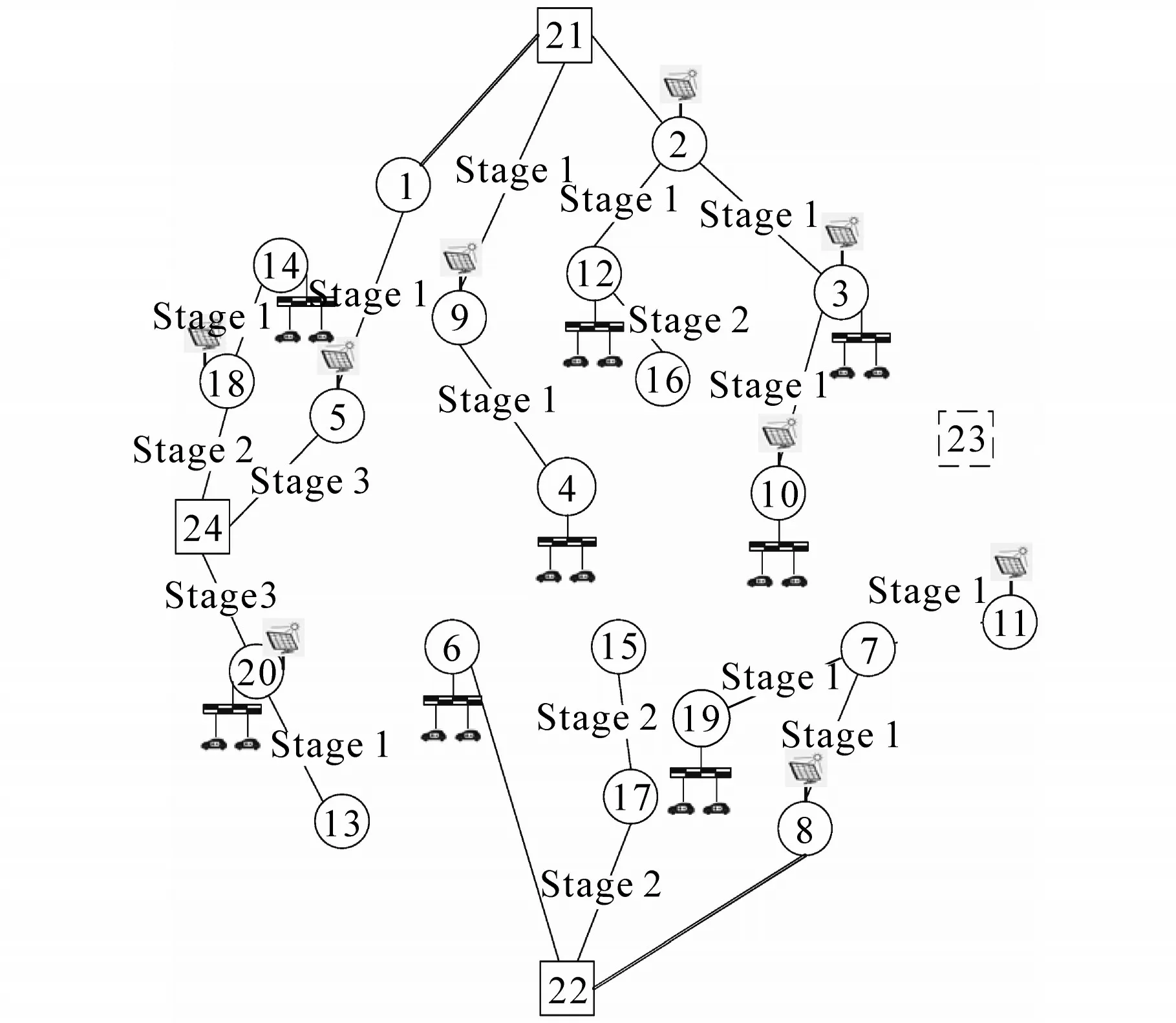
图6 考虑光伏和电动汽车的三阶段规划拓扑图Fig.6 The three-stage planning topology with PV and EV

结合表3 和图3～图6 以及优化过程数据分析如下。

联合规划拓扑图在4种场景下有显著的差异，在同一场景下的不同规划阶段也发生了变化，具体而言，其新建和投用的变电站、线路、光伏电站和电动汽车充电站不同，因而形成的配电网网架结构也不同。随着配电网负荷的阶段性增长，除了投资成本以外，变电站生产成本、运维成本和网络损耗在内的运行费用都呈现出了阶段性递增的趋势，并且考虑光伏电站和电动汽车充电站可有效减少系统规划总成本。

与基准规划场景Ⅰ相比，场景Ⅱ在节点2，3，5，8，10，11，18，20 配置光伏电站后，三阶段规划拓扑图中的线路结构及变电站投资方案均发生了变化，可以看出：1）配置光伏电站能够延缓或减少配电网中变电站的投资，降低变电站的出力。场景Ⅱ中，23 号变电站不进行投建规划，24号变电站在第2 阶段才投入使用；2）配置光伏电站会产生更高的投资和维护成本，但这种预期的费用增长能够被生产成本的降低所补偿。场景Ⅱ新建了8 座光伏电站，因而其投资成本比场景Ⅰ高得多。但相应的由于光伏发电能够承担配电网的一部分生产负荷，减少大量配电网从主网购买电能，总费用成本相对于场景Ⅰ减少了51.36%；3）光伏电站的参与使得配电网规划总成本有较大程度的降低，其规划总费用成本也在逐阶段递减。场景Ⅱ中3个阶段的规划总成本费用逐步递减，并且每个阶段的费用相差较大，这也使得投资者会在投建初期承担较大的经济压力；4）将光伏电站集中在高负荷区域，可以避免线路潮流所带来的网络损耗，达到分布式光伏就地消纳的积极效果。从场景Ⅱ和其他场景的规划成本可以看出，在有光伏电站的情况下，支路和变压器的网络损耗均低于没有光伏电站的情况。

与基准规划场景Ⅰ相比，场景Ⅲ在节点3，4，6，10，12，14，19，20 配置电动汽车充电站后，配电网的线路结构发生了变化，这表明规划方案的线路供电方式发生了变化。可以看出：1）电动汽车充电站的接入加快了配电网中线路的投资和使用。场景Ⅲ中，线路7—19，20—24 在第1 阶段提前新建以满足节点19 和节点20 的电动汽车充电负荷；2）配置电动汽车充电站会产生更高的投资和运维成本，但这种预期的费用增长能够被运营收益所补偿。场景Ⅲ中，在第1 阶段新建了8 座电动汽车充电站，因而第1 阶段的投资成本比场景Ⅰ高得多。但电动汽车充电站通过向用户提供充电负荷能够赚取一定的运营收益，抵消其投资成本的增加，总费用成本相对于场景Ⅰ减少了12.11%；3）电动汽车充电站接入后通过充放电可以改变整个配电网的潮流分布，但同时会带来更大的网络损耗。电动汽车充电负荷需求加大了网络中的能量流动，从而产生更大的网络损耗；4）原有建设的线路会影响后续线路的铺设。在场景Ⅲ中，可直接从22 号变电站铺设线路到13号负荷点，但实际上供给节点13 的功率由22—6—13 线路进行传输，这可能是由于22—6 线路是原有已投入使用的线路，22—6—13 线路的投资费用比22—13线路的投资费用更低。

与前3 种场景相比，在考虑光伏和电动汽车充电负荷场景Ⅳ下，联合规划方案中的线路均不相同。场景Ⅳ在节点2，3，5，8，9，10，11，18，19配置光伏电站，在节点3，4，6，10，12，14，19，20配置电动汽车充电站。可以看出：1）光伏和电动汽车的联合规划所得到的规划方案总成本是最低的。电动汽车充电负荷的接入加快了光伏电站的新建，虽然前两个阶段的投资成本很高，但相应地能够在更大程度上减少变电站的生产成本，而且还实现了更大的电动汽车充电站收益；2）对该配电网系统来说，考虑充电负荷所带来的运营收益能够补偿要付出的生产成本，考虑光伏电站所带来的电能生产能够补偿要付出的投资成本；3）在考虑年通货膨胀调整利率的前提下，为了节约线路的铺设费用，可以采取提前1 个阶段铺设但暂不投入使用的做法。

在4 个场景下的各负荷水平下，失负荷成本均为0，说明所提出的规划方案可保证各节点负荷需求，这个结果也验证了模型的适用性。

4 敏感性分析

本文在场景Ⅱ和场景Ⅲ下对该模型中光伏电站的渗透水平和电动汽车接入水平对经济性的影响进行分析评估。不同光伏和电动汽车接入率下的总成本净现值如图7所示。

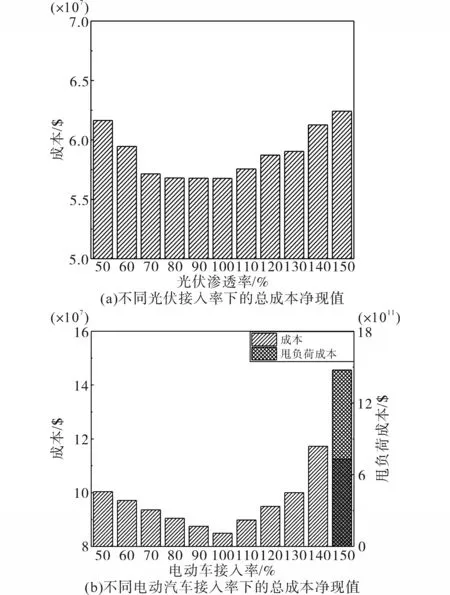
图7 不同光伏和电动汽车接入率下的总成本净现值Fig.7 The EPV with different access rates of PV and EV

4.1 光伏渗透水平对配电网规划的影响

图7a显示了光伏在50%到150%的渗透水平下，总成本净现值的变化情况。可以看出：随着规划方案中配置的光伏发电容量进一步上升，总成本净现值呈现出先减少后增加的趋势，并且从规划方案中可以知道，在一定的渗透率下联合规划方案会保持不变。说明光伏发电配置容量达到一定阈值以后，光伏电站的选址将固定在对规划影响最显著的位置。当光伏发电渗透率达到80%以上时，光伏发电总成本不再随光伏容量增加而减少，相反的，当光伏渗透率过高时，总成本会随之升高。若每一个负荷节点都能配备光伏电站并实现太阳能的就地消纳，那么整个配电网系统的生产成本和网络损耗将会大大降低，但随之而来的系统投资成本也会大大升高，因此投建光伏电站的关键在于权衡好两种成本值。

4.2 电动汽车接入水平对配电网规划的影响

图7b 显示了电动汽车在50%到150%的接入率下，总成本净现值的变化情况。可以看出：随着规划方案中配置的电动汽车充电站容量的增加，总成本净现值呈现出先减少后缓增而后激增的趋势。出现总成本激增的情况是由于当电动汽车接入率达到150%时，失负荷成本不再等于0，说明配电网节点出现了失衡现象，过高的失负荷成本也使得整个配电网规划的总成本超出了预期。随着负荷的增长尤其是电动汽车充电负荷的接入，过高的负荷需求在系统线路容量、变电站出力以及节点电压的限制下容易发生节点失衡现象。目前看来，配置光伏电站是一种较好的防止配电网出现节点失衡现象的解决方案。