滩地刚性植物消浪作用特性研究
2023-09-19张之琳黄本胜
张之琳,黄本胜,刘 达,邱 静
(1.广东省水利水电科学研究院,广东 广州 510635;2.河口水利技术国家地方联合工程实验室,广东 广州 510635;3.南方海洋科学与工程广东省实验室(珠海),广东 珠海 519082)
1 研究背景
红树林等滩地植物的消浪作用实质上是波浪与植物相互作用导致波浪能量的耗散,而林带与水体相互作用复杂,量化成熟期滩地植物的消浪作用是提升生态海岸韧性、合理利用滩涂资源的基础[1-3]。
目前针对植物消浪作用的研究方式主要有原型观测[1,4-5]、物模试验[6-7]及数模计算[8-9],其中,植物消浪系数表征波高在林带前后的变化,是量化植物消浪效果的关键系数。原型观测方面,由于观测地点及其地形地貌、植物类型及其种植结构的差异,不同学者观测到的植物消浪作用虽有所差异,但已知盐沼湿地的消浪效果远优于潮泥滩地、林带内波高呈指数衰减等规律[4,10]。物模研究方面,章家昌[6]根据试验结果得到植物消浪系数与来波波长、林带宽度、林木主干和枝叶遮蔽系数的定量表达式。虽然后续研究中纳入了波浪类型[11]、初始波高[7]、波周期[12]、波陡[7,13]、波流耦合作用[12]、植物淹没度[12]、植物垂直密度分布[14]、杆群刚度[15]、植物形态[7]等影响因素,但植物消浪系数的计算方法仍是以文献[6]为主。数模研究中,植物作用一般通过摩擦项体现[16-17],模型中往往以植物对波浪水流的阻力研究作为机理研究的基础,其中,求解拖曳力系数是量化植被在水中阻力的关键。在以往研究中[18-20],基于波浪通过林带后波高消减这一规律,根据波高消减模型率定得到阻尼因数,再通过阻尼因数与拖曳力系数及其他易于测量的参数(如滩地水深、平均植物密度)之间的联系,得到拖曳力系数的值,最后通过非线性回归得到拖曳力系数与雷诺数、邱卡数等参数之间的关系式以供数模计算。然而,拖曳力系数受不同试验工况(如植物密度)影响与重要参数呈不同的非线性关系[14,20]。
本文在文献[6]基础上,基于“林带越宽、植物越密、水深越浅,植物消浪作用越强”的一般试验规律[21],结合99组物模试验结果,分析提出了新的植物消浪系数计算方法,通过153组试验数据开展了验证,并与规范方法结果进行了对比,揭示了影响植物消浪机理的关键无量纲参数,可根据地区消浪要求,结合植物直径、高度和水深、波要素条件,设计合理的植物种植宽度、密度,实现滩涂资源的有效利用。此外,得到的植物拖曳力系数计算方法可为相关数模研究提供基础。
2 理论基础
2.1 计算植物消浪系数的规范方法常以波高的变化表征波浪能量的变化,以植物消浪系数量化滩地植物对波浪的消减作用。《海堤工程设计规范》(GB/T 51015—2014)基于文献[6]提出防浪林消浪系数(β)可按下列公式计算:
(1)
(2)
(3)
则林带消浪后的波高(Hout)为:
Hout=(1-β)H0
(4)
2.2 两种波高消减模型波高在种树带中的衰减规律主要可由两种波高消减模型描述。一种是Dean[22]提出的林带沿程波高(H(X))符合互反函数的消减模型:
Kv=H(X)/H0=1/(1+α′X)=1/(1+αx) (0≤x=X/L≤1)
(5)
式中:Kv为无量纲缩尺相对波高,β(=1-Kv)即为消浪系数;α′为阻尼因数,m-1;α(=α′L)为缩尺阻尼因数;X为与林带前端的距离,m;x为与林带前端的缩尺距离。
另一种是Kobayashi等[23]根据深度淹没的人工巨藻(artificial kelp)试验并假设H(X)3≈H0H(X)2,得到通过林带的沿程波高呈指数消减:
Kv=H(X)/H0=exp(-k′X)=exp(-kx)
(6)
式中:k′为指数阻尼因数,m-1;k(=k′L)为缩尺指数阻尼因数,根据已有试验数据其取值范围为[0,1)。Zhang等[24]结合两种模型,得到缩尺阻尼因数与缩尺指数阻尼因数的关系式:
α=2k/(2-k)
(7)
当植物深淹没消浪效果有限时[23],k值接近于0,α值大于但接近于k值,此时α≈k[20]。
2.3 传统拖曳力系数求解方法Dean[22]、Dalrymple等[25]、Kobayashi等[23]提出了阻尼因数或指数阻尼因数与拖曳力系数(CD)的关系式:
α′=CDdNH0/6πh
(8)
(9)
(10)
式中:d为植物直径,m;N为单位面积植物数量,株/m2;h为滩地水深,m;kw为波数,m-1;ls为植物在水中的高度,m,若植物为非淹没工况其值等于滩地水深h;dv为植物平均直径,m,即波浪传播方向上单位高度的面积。
因此,拖曳力系数的率定方法可归纳如下:①结合Dean[22]提出的消减模型式(5)及阻尼因数与拖曳力系数的关系式(8);②结合式(5)及Dalrymple等[25]建立的关系式(9);③结合Kobayashi等[23]提出的消减模型式(6)及指数阻尼因数与拖曳力系数的关系式(10);④根据式(6)率定指数阻尼因数,基于关系式(7)得到阻尼因数,再结合经典关系式(9)。根据文献[20]分析,方法①和③仅适用于植物淹没工况,方法②和④能在植物淹没和非淹没工况下表现良好。
将率定得到的拖曳力系数与雷诺数、邱卡数等重要参数关联得到非线性关系式[18-20],并结合下式是数模中计算水流通过植物杆群的阻力(FD)的常用方法:
(11)
式中:ρ为流体密度,kg/m3;A为阻力面积,m2;U为流速,m/s。
2.4 阻尼因数与拖曳力系数植物消浪系数越大代表植物消减波浪能量的作用越强,但式(1)较复杂且尚未能直观显示影响植物消浪作用的关键因素。根据波高消减模型,若想消浪系数越大,则林带需要更大的(指数)阻尼因数。然而,阻尼因数历来是通过率定得到,现有成果对其仍了解甚少。
而且,式(8)和式(9)显示,植物平均直径、植物密度、入射波高越小,水深、阻尼因数越大,则拖曳力系数越大。其中,“植物直径、植物密度越小,拖曳力系数越大”与以往对植物消浪效果研究的认识不相符,可能因为式中的阻尼因数本身又与植物直径、植物密度等参数有关,拖曳力系数的大小受多因子共同影响。因此,进一步研究影响阻尼因数的关键因素及定量表达式,有助于增加对植物消浪系数和拖曳力系数的认识。
3 植物消浪作用特性分析
3.1 阻尼因数法计算植物消浪系数为研究植物消浪作用,本文收集了Wu等[26]、Hu等[12]、Wu等[13-14]、Zhang等[20]等文献中共计99组在水平滩地上开展的消浪试验数据。各试验工况不同,例如模拟植物有的为淹没状态,有的为非淹没状态。首先通过收集的99组数据研究缩尺阻尼因数计算表达式。已有研究表明,种树带情况对波浪的影响巨大,且林带密度(N)越大,植物消浪效果越好[6-7];植物淹没度(ls/h)大于等于1时,消浪作用强于其小于1时[16,20]。结合文献[21]归纳的一般试验规律,分析得到可以表达林带情况的无量纲参数:波浪传播方向上植物面积占横截面比例NdvlsL/h,其中,单位植物占比:dvls/Bh(B为Y方向距离,m);植物数量:NLB。因此,把缩尺阻尼因数看作与具有物理意义的无量纲因子NdvlsL/h有关,则该因数可用下式表示:
α=α(NdvlsL/h)
(12)
植物淹没状态是影响植物消浪作用的关键因素之一[18,20]。因此,区分淹没和非淹没工况,基于不同模拟植物的99组数据进行规划求解,得:
α=0.1840(NdvlsL/h)0.5492θ1.2750
(13)

α=0.1840(NdvL)0.5492(非淹没工况)
(14)
α=0.0760(NdvlsL/h)0.5492(淹没工况)
(15)
阻尼因数法计算植物消浪系数βα的表达式为:
βα=1-Kv=1-1/(1+α)
(16)
所有组次植物消浪系数α法的计算值与实测值对比见图2。其中,实测值为根据实测沿程波高和波高消减模型所得的结果;计算值为每组工况根据实测参数由表达式计算得的结果;预测值为根据表达式的理论计算结果。图中不同符号表示不同学者的研究,实心符号表示植物非淹没工况,半填充符号表示植物淹没工况(下同)。结果显示,来自不同实验室的试验数据能较好地被综合分析。99组工况得到的实测值与计算值结果接近,线性拟合结果斜率为0.9771,修订判定系数达0.9484。计算值几乎在预测值±0.2范围内,考虑试验误差,上述消浪系数计算方法是可行的。
进一步地,根据式(13)和(16)可以快速预测相关参数变化对植物消浪效果的影响。例如,根据试验结果,非淹没林带宽5m、密度25株/m2时植物消浪系数值为0.43;根据式(16),此时缩尺阻尼因数值为0.75。当密度50株/m2时,N增加一倍,根据式(13),α为原来的1.46倍,即此时α值为1.10,对应β值为0.52;与试验结果“林带宽5 m、密度50株/m2时的波高消减率约为52%”一致。
3.2 指数阻尼因数法计算植物消浪系数类似的,对缩尺指数阻尼因数规划求解得:
k=0.1765(NdvL)0.4331(非淹没工况)
(17)
k=0.0939(NdvlsL/h)0.4331(淹没工况)
(18)
指数阻尼因数法计算植物消浪系数βk的表达式为:
βk=1-Kv=1-exp (-k)
(19)
所有组次植物消浪系数k法的计算值与实测值对比见图3。结果显示,99组工况得到的实测值与计算值线性关系良好,拟合结果修订判定系数为0.9481,且计算值基本在预测值±0.2范围内。结果说明式(17)和(18)可以较好地描述缩尺指数阻尼因数,与式(19)搭配可以有效计算植物消浪系数。
同理,根据式(17)至(19)可以预测参数变化后植物消浪效果的变化情况。例如,根据试验结果,非淹没林带宽5 m、密度25株/m2时,根据式(19),k值为0.56。N增加一倍时,根据式(17),k为原来的1.35倍,即此时k值为0.76,对应β值为0.53;与试验结果接近。
此外,若考虑更多影响因素,在式(13)至(18)中增加其他无量纲数可能得到更好的拟合结果,但本文方法抓住了影响植物消浪作用的最主要因素且关系式相对简单,后续可加入例如植物排列方式、波浪要素等因素开展研究。
3.3 两种阻尼因数的关系不同研究中,根据实测参数由式(13)得的缩尺阻尼因数计算值与由式(17)(18)得的缩尺指数阻尼因数计算值的关系见图4。结果显示,α值小于约0.4时,α与k计算值接近[20]。而且,对于淹没和非淹没工况,通过式(7)可以很好地拟合α与k的关系,佐证了阻尼因数与指数阻尼因数的计算方法以及式(7)的合理性。
3.4 根据消浪系数计算林带后波高至此,通过入射波高和消浪系数计算表达式可以得到林带消浪后波高。Hout根据α法和k法的计算值与实测值的对比分别见图5和图6。
结果显示,两种方法都可以良好地预测林带后波高;两者计算值与实测值线性关系的修订判定系数都达到约0.992,斜率接近于1。考虑到试验误差及不同工况,结果令人满意。两种方法的计算值对比结果显示(图略),线性关系斜率0.9893,修订判定系数0.9998,进一步说明两种波高消减模型都可以很好地描述波浪在林带拖曳作用下波高的消减情况。
3.5 根据阻尼因数计算拖曳力系数如果将阻尼因数由式(13)带入式(8)和(9),可得到拖曳力系数的计算表达式:
(20)
(21)
当植物非淹没时,两式可简化为:
(22)
(23)
结果显示,拖曳力系数CD与ls正相关,与dv、H0、N[18]、L等参数负相关。然而,根据试验结果,植物消浪作用与上述参数并无明显直接关系,可能因为拖曳力系数本身是一个数值解,物理意义并不明确,植物消浪作用的物理意义主要由阻尼因数及消浪系数体现。
拖曳力系数根据式(20)(21)计算值与根据经典Dalrymple等[25]公式率定值(第2.3节中方法②)的对比关系分别见图7、图8。结果显示,计算值与率定值接近,绝大多数情况下,计算值在预测值0.5~2倍范围内。考虑到试验误差、多种工况以及拖曳力系数的性质,计算结果基本可行,上述拖曳力系数计算方法可酌情应用于数模研究。
4 物模试验概况
4.1 本次试验设计本次物理模型试验在广东省水利水电科学研究院河口水利技术国家地方联合工程实验室的波浪水槽中进行,水槽长80 m、宽1.8 m、高2.6 m。
本次水力模型水平滩地工况的总体设计及模型布局、仪器设备、模型树与文献[20]一致,但模拟植物材料、种树带宽度、波浪参数等设计不同。此外,基于自然规律下滩地坡度一般为1∶15~1∶20,在水平滩地模型的基础上设计了坡度为1∶20缓坡滩地模型试验(见图9),以研究根据水平滩地试验数据所得的植物消浪计算方法在缓坡滩地上的适用性。试验模拟植物除了模型树[20]还采用了直径0.01 mPVC材料的刚性柱。
根据文献[27],中国大陆地区最大面积的连片红树林生长区内引种的无瓣海桑林平均高约5.5 m;本地的白骨壤、木榄、红海榄、秋茄、桐花林高度分别约2.3 m、2.9 m、4.2 m、3.5 m、2.6 m;保护区内小树密度0.15~0.50株/m2、大树密度0.15~0.25株/m2。因此,本试验设计原型高3 m和5 m的模型树,即模型树、刚性柱高度采用0.3 m、0.5 m,植物密度采用25株/m2、50株/m2。模型中,种树带宽度采用0.5 m、2 m、3 m、4 m、5 m、6 m,滩地水深采用0.3 m、0.5 m、0.7 m。缓坡滩地前缘水深为0.5 m时,植物为非淹没;前缘水深为0.7 m时,种树带计为淹没状态。缓坡滩地时计算滩地水深(h)考虑两种:①植物区水深的平均值;②缓坡滩地前缘水深。经试验验证,两种考虑的结果几乎一致,为简单化处理,计算滩地水深采用缓坡滩地前缘水深。
表1中罗列了不同影响因素组合下的113种工况,对应都测量了无植物时的空白试验,Hori为G0处初始波高;G1处的波高为种树带入射波高H0。
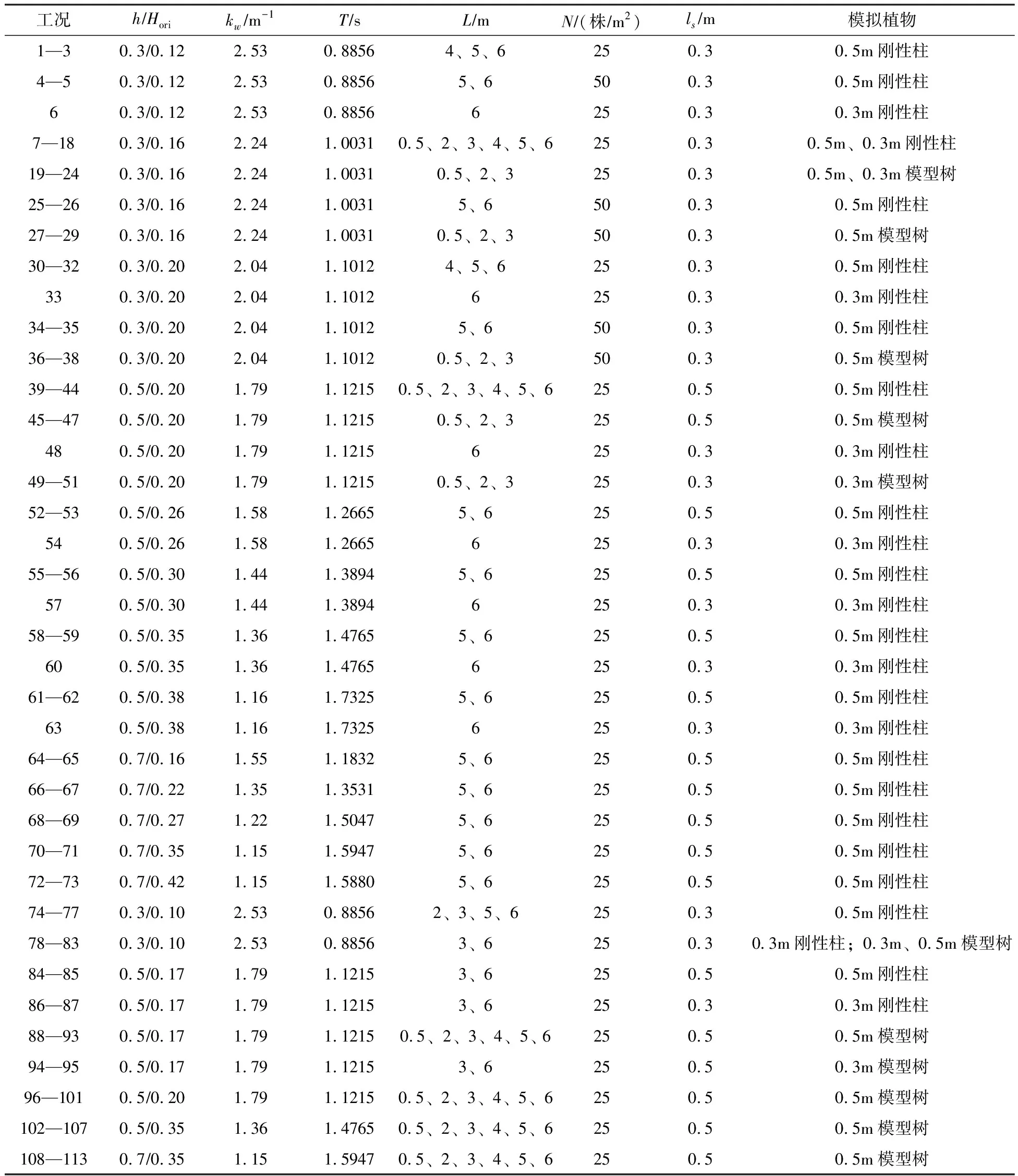
表1 刚性柱和模型树试验工况
4.2 历史数据归集为更充分研究植物消浪作用特性,本文还收集了谭超等[15]、陈晖[28]文献中不同工况共40组试验数据。谭超等[15]在长66 m、宽1.0 m、高1.6 m的波浪水槽中,采用4种不同刚度但外形相同的圆柱形硅胶棒开展了植物杆群消浪试验;模拟植物直径0.01 m、高度0.2 m,林带密度400株/m2、宽度2 m;滩地水深0.15 m,规则波波高0.05 m、波周期1.34 s。陈晖[28]试验水槽长20 m、宽0.6 m、高0.6 m,植被区长8 m,模拟植物PVC管直径0.02 m、高度0.20 m;滩地水深采用0.15 m、0.25 m,植物密度采用139株/m2、556株/m2;入射波高采用0.03 m、0.05 m、0.07 m、0.09 m,波周期采用0.6 s、0.9 s、1.2 s;共开展36组规则波实验。40组试验资料的纳入有利于验证本文所提方法的适用性。
5 结果与讨论
5.1 植物消浪系数计算方法验证用本次试验的113组和收集的40组数据验证消浪系数计算方法。不同工况消浪系数根据阻尼因数法和指数阻尼因数法的计算值与实测值对比分别见图10和图11。

图1 波浪传播方向上植物面积占横截面比例示意图
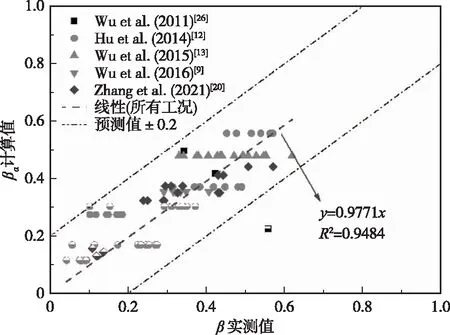
图2 消浪系数α法计算值与实测值对比

图3 消浪系数k法计算值与实测值对比
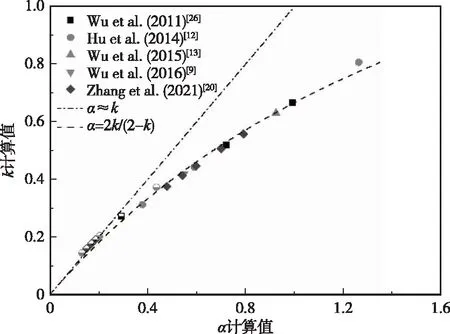
图4 99组工况α与k计算值对比

图5 Hout阻尼因数法计算值与实测值对比
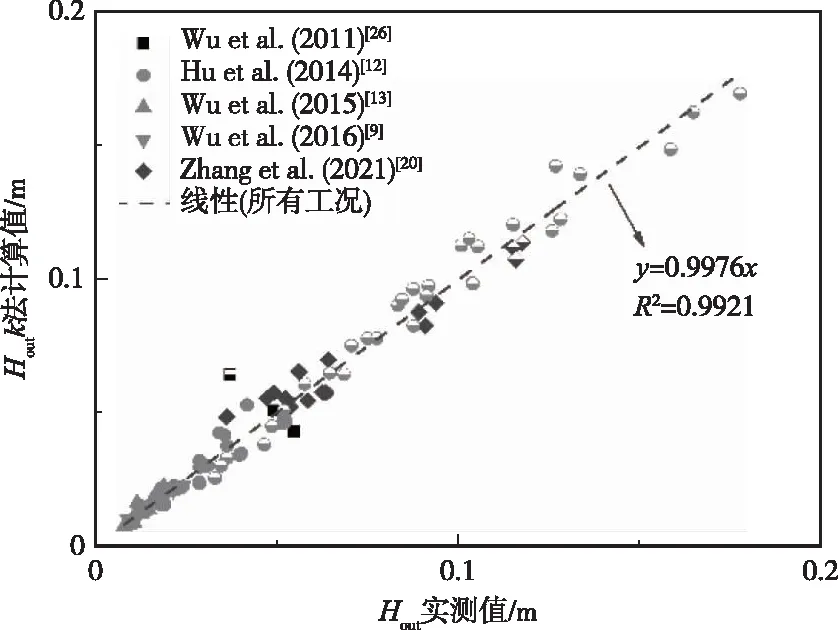
图6 Hout指数阻尼因数法计算值与实测值对比
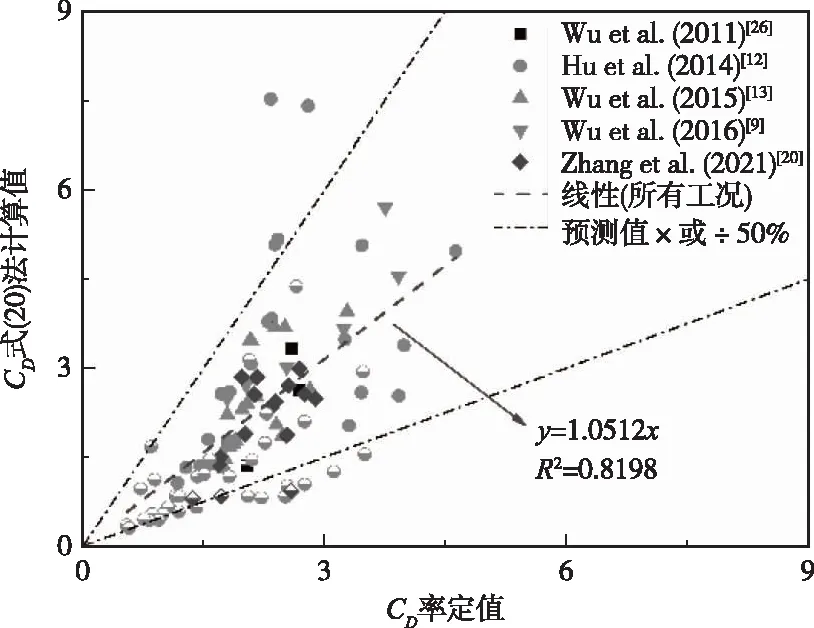
图7 拖曳力系数式(20)计算值与率定值对比
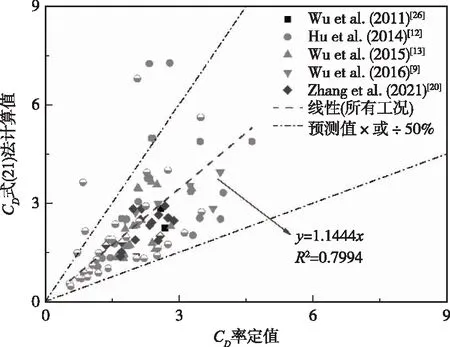
图8 拖曳力系数式(21)计算值与率定值对比
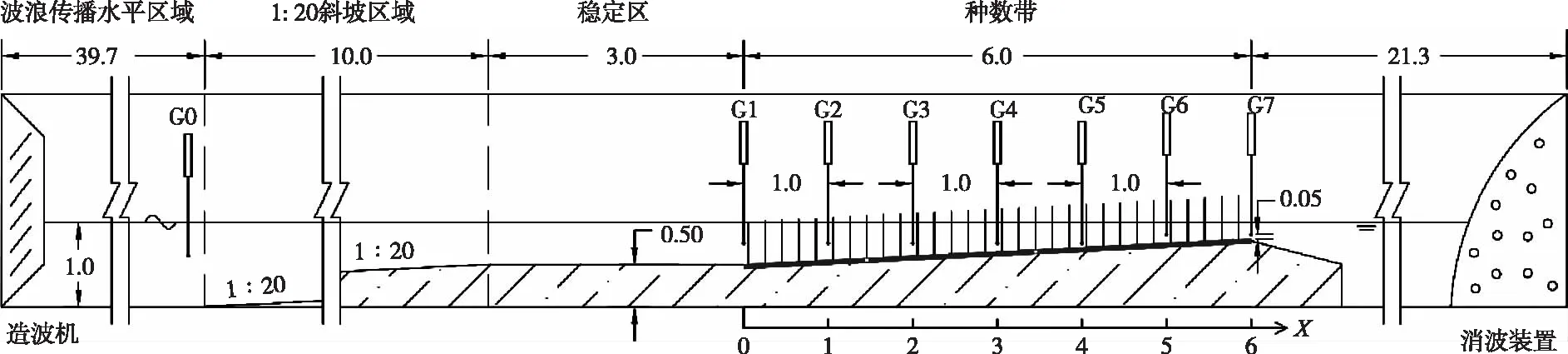
图9 1∶20缓坡滩地工况试验设置(滩地前缘水深0.5 m时,单位:m)
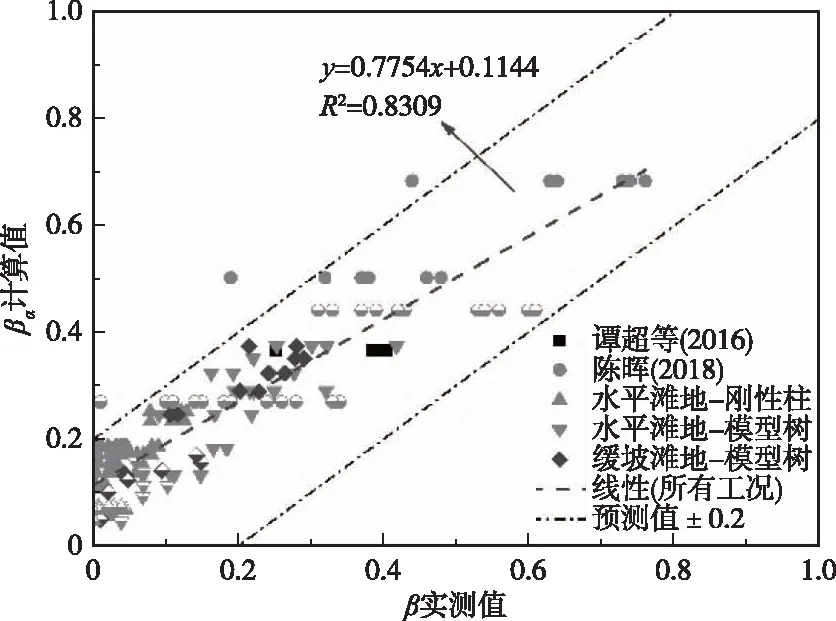
图10 验证工况消浪系数α法计算值与实测值对比

图11 验证工况消浪系数k法计算值与实测值对比
结果显示,消浪系数实测值较小的工况,其计算值可能略高于实测值;消浪效果较好时,计算值接近于实测值。无论模型树或刚性柱,规则波或不规则波,植物淹没或非淹没,各工况消浪系数计算值基本在预测值±0.2范围内。异常值为波周期0.6 s工况,可能跟试验测量波高精准度有关[28]。
值得注意的是,消浪系数计算方法尚未考虑不同刚度杆群的影响。然而,根据文献[15],植物抗弯弹性模量值不小于0.39 GPa时可达到预期消浪效果。根据木材弹性模量资料,所有常见树木都满足该刚度,即计算方法适用于常见防浪树木。
5.2 林带后波高计算方法验证用153组试验数据验证林带消浪后波高计算方法。不同工况Hout根据α法和k法的计算值与实测值对比分别见图12和图13。
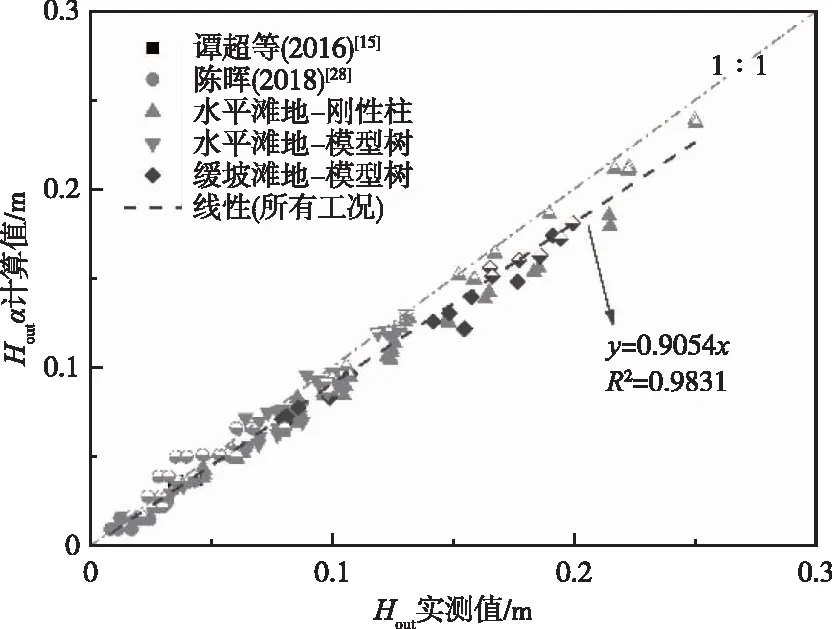
图12 验证工况Houtα法计算值与实测值对比
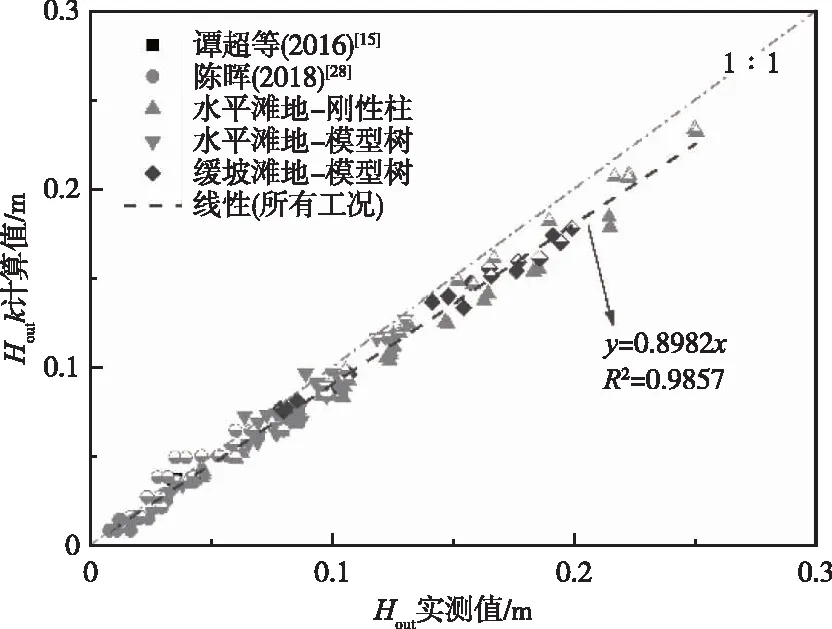
图13 验证工况Houtk法计算值与实测值对比
结果显示,所有工况两种方法计算值与实测值线性关系的修订判定系数分别高达0.983、0.986;计算值接近于实测值,说明Hout计算方法效果好,能有效计算植物消浪作用。波高较大时,计算值可能偏小,即计算方法略高估了消浪效果较差时(例如刚性柱dv较小)滩地植物的消浪作用。此外,基于水平滩地工况的计算方法略高估缓坡滩地工况下的试验效果,可能由于波浪波高较大时在水深较浅时易破碎,此时设计波长等参数与实际操作不符导致计算结果出现偏差。实际中可通过增加安全系数的方法进行修正。
5.3 与规范计算方法对比针对模型树试验,包括文献[20]的16组工况,水平和缓坡滩地工况下,规则波和不规则波作用下,根据规范方法的计算值与实测值对比见图14,根据规范方法和本文方法(以阻尼因数法为例)所得的计算值对比见图15。
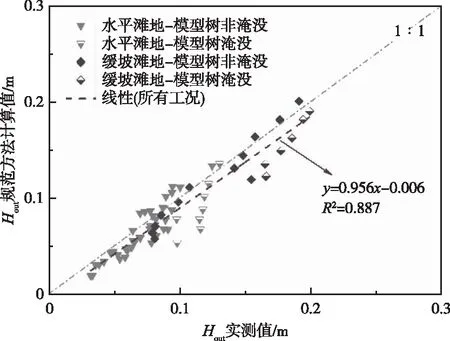
图14 Hout规范方法计算值与实测值对比

图15 Hout规范方法与本文方法计算值对比
结果显示,本文方法计算得到的林带后波高与规范方法接近,尤其对于水平滩地植物非淹没工况,进一步说明了本文方法的可靠性。规范方法仅考虑种树带宽度、波长、植物遮蔽系数、植物密度,未考虑植物高度、水深等垂向要素,在植物淹没时可能导致预测的消浪系数偏高从而预测的林带后波高偏低(图14)。本文方法考虑了植物淹没情况,有利于准确描述更多工况下的植物消浪作用。此外,两种方法理论上都未考虑滩地形态的影响,由计算值低于实测值可推测缓坡滩地时植物的消浪作用比同等条件下水平滩地偏弱,实际中可通过增加安全系数的方法稍作修正。
6 结论
通过海岸防浪林消减波浪能量是一种基于自然的解决方案。为了解波高消减规律,文献[22-23]提供了两种可靠的消减模型:互反函数和指数函数。本文通过99组试验资料,基于波高消减模型和一般规律分析提出了影响植物消浪作用的关键无量纲参数,可用于求解植物消浪系数、林带后波浪波高、植物拖曳力系数。相关植物消浪作用计算方法又由本次试验的113组和收集的40组数据进行了验证,最后对比了由本文方法与规范方法的计算结果。主要结论如下:
(1)波高消减模型中的缩尺(指数)阻尼因数与波浪传播方向上植物面积占横截面比例NdvlsL/h这个无量纲数密切正相关,揭示了植物消浪机理,可快速研判相关参数变化对植物消浪效果的影响。植物非淹没时,缩尺阻尼因数α=0.1840(NdvL)0.5492,缩尺指数阻尼因数k=0.1765(NdvL)0.4331。α和k基本符合α=2k/(2-k),这增加了对消减模型的约束,有助于更准确研判植物消浪作用。相应的植物消浪系数、林带后波高、拖曳力系数结果也说明了α和k定量表达式的有效性。而且,相较于拖曳力系数,阻尼因数及消浪系数更能直观体现植物对波浪的消减效果。
(2)153组试验数据良好地验证了消浪系数和林带后波高的计算方法。波高较大时,计算方法可能略高估消浪效果较差时滩地植物的消浪作用;滩地缓坡形态也可能对结果产生一定影响,实际中可考虑相关系数保证水安全。
(3)与规范方法相比,本文方法考虑了植物淹没程度的影响,拓展了消浪机理计算方法的适用范围,直观揭示了种树带密度、宽度、高度、植物平均直径、水深等对植物消浪作用的影响,可根据消浪要求合理设计植物种植宽度、密度以实现滩涂资源的有效利用,为指导植物防护工程设计提供依据。
