基于深度强化学习的智能兵棋推演决策方法

胡 水

（中国人民解放军陆军指挥学院，南京 210000）

0 概述

随着高新技术在军事领域的不断发展运用，武器装备的性能参数和造价越来越多，现代作战体系越来越复杂，作战训练成本也同步激增。文献［1］介绍为控制训练成本和节约人力物力资源，各国使用仿真技术模拟作战训练。近年来，以深度强化学习为代表的人工智能技术快速发展，直接从模拟战场原始数据中快速提取特征，使得对战场态势进行描述、感知并进一步自主决策成为可能。将人工智能技术应用于兵棋推演，形成战术兵棋智能体，对培养智能化作战指挥员打赢未来战争具有深远意义。

文献［2］通过兰彻斯特模型对兵棋的胜负过程和作战结果进行仿真分析，为兵棋规则的设计提供依据和参考。文献［3］针对六角格回合制兵棋，使用AlphaZero 深度强化学习来自动学习作战游戏过程。文献［4］将模糊Petri 网的知识表示与推理方法应用于兵棋推演，在图的特征中用不同符号表示不同变量，从而形成1 个简洁的PN 映射，并将其用于兵棋推演的兵力表示和推理决策。文献［5］通过对兵棋推演数据进行采集分析和处理，并基于数据搭建兵棋推演分析系统。文献［6］介绍目前兵棋推演方面的研究面向规则智能算法、作战方案评估等。智能算法多基于规则和数据分析，因此，开展基于深度强化学习的兵棋推演算法研究有助于提高兵棋推演的智能化水平，相较于人与人之间的兵棋推演对抗，基于强化学习的兵棋推演能够筛选更多的数据。文献［7］利用马尔可夫决策过程、神经网络等方法，增强AI 推演行动反馈及指挥策略应用能力，以逐步提高AI 在兵棋系统的对抗推演水准。文献［8］深入分析军事辅助决策走向智能化所面临的难题和挑战，仅根据深度学习是无法实现AI 对于高位输入做出最优的决策，因此，针对已有AI 在人机对战中所做的失误决策，提出将深度神经网络与强化学习算法相结合的新一代智能兵棋推演算法。

目前，深度强化学习的研究主要应用于博弈方向以及人机对抗方向，其中，深度Q 学习网络（Deep Q-learning Network，DQN）能有效完成对环境状态的态势理解与决策构建的准确性。文献［9］介绍记忆函数的引入将在可自我博弈的基础上完成对模型的快速训练并获得较优的准确性。但是，在兵棋推演系统中智能体设计上，面对瞬息万变的战场环境与错综复杂的作战场景，智能体的数据学习周期较长，策略产出与模型训练收敛都需要较长时间。文献［10］基于深度强化学习的思想和方式实现智能算法，虽然提高了AI 在兵棋系统的对抗推演水准，但是较长周期的策略产出是其最大的弊端。

本文聚焦于智能体在兵棋推演系统中自主决策产出过程的改进，在传统策略-价值网络的基础上提出适用于兵棋推演的低优势策略-价值网络（Low Advantage Policy-Value Network，LAPVN）智能决策模型，有助于智能体加快产出作战决策，设计符合兵棋规则的战场态势感知方法，提高策略的合理性。

1 相关理论

1.1 智能体的状态-价值函数

状态-价值函数Vπ(st)定义如下：

其中：Vπ(st)用于评判战场状态st下策略函数π的好坏程度。在大多数场景中智能体的状态-价值函数是离散变量。策略函数π由策略网络π(a|st；θ)近似表示。智能体在t时刻的状态-价值函数如下：

其中：Qπ(st,a)表示t时刻动作-价值函数，表示在状态st下执行动作a后获得的价值。若消去环境状态S可得：

由于V(S；θ)值可用于反映在环境状态S下策略函数π的完备性，因此当J(θ)越高时，V(S；θ)也越高，说明策略网络对于完备策略函数的近似度越高，即策略网络做出的策略是一个完备的策略。但是J(θ)具有一定的阈值约束。文献［11-12］利用策略梯度算法提高J(θ)。策略梯度的定义［13］如式（4）所示：

通过梯度上升不断更新策略网络π(a|S；θ)参数θ。

1.2 近似动作-价值函数

在策略梯度算法中，动作-价值函数Qπ并不是已知的，且直接计算需要大量的计算资源。因此，在策略梯度算法中将动作-价值函数Qπ(st,at)近似为qt。近似方法通常有Reinforce 和神经网络近似方法。

Reinforce 方法：假定智能体在T时刻完成计算，在完成过程中统计(s1,a1,r1,s2,a2,r2,…,sT,aT,rT)。此时可得到任意时刻t的折扣回报：

由于动作-价值函数定义Qπ(st,at)=E[Ut]，ut是动作-价值函数Qπ的无偏估计，因此可用ut近似Qπ，即：

其中：qt为当前t时刻的动作-价值函数值。

神经网络近似方法：文献［14-15］借鉴了DQN的思想，利用另一个卷积神经网络Qπ(w)近似动作-价值函数。

1.3 策略-价值网络

策略网络π(a|S；θ)用于近似策略函数π，给出当前状态S下的动作a，通过策略梯度算法中梯度上升方式更新网络参数θ。价值网络q(S,a；w)用于近似动作-价值函数Qπ，评判动作a的好坏程度，以改进策略网络。文献［16-17］通过时间差分（Temporal-Difference，TD）算法中梯度下降方式更新网络参数w。此时，状态-价值函数如式（7）所示：

状态-价值函数用于对当前环境状态打分，评分高低反映智能体可获胜的概率，更新θ是为了增加V(S；θ,w)，价值网络q(S,a；w)在θ更新过程中对动作打分起着监督作用。更新w是为了提高对动作评分的精准度，环境给出的奖励r起监督作用。

算法1 所示为在神经网络中θt和wt的更新过程，st、θt、wt作为输 入，θt+1、wt+1作为输 出，步骤主要有：

1）对at～π(⋅|st；θ)进行采样，得到动作at；

2）执行动作at，得到新的环境状态st+1；

5）计算δt=qt-(rt+γ⋅qt+1)；

6）计算价值网络梯度∂wt与策略网络梯度∂θt：

7）更 新θ与w：wt+1←wt-α⋅δt⋅∂wt，θt+1←θt+β⋅qt⋅∂θt；

8）得到7）中wt+1与θt+1。

2 基于深度强化学习的智能兵棋推演决策方法

针对兵棋智能体决策模型训练时间长、策略产出效率较低的问题，本文提出一种策略网络更新的改进方法，以缩短策略产出周期，加快模型训练的收敛速度。

智能兵棋推演决策模型框架由战场态势感知模型、作战场景判断模型、智能决策模型与作战动作指令模型组成，如图1 所示。

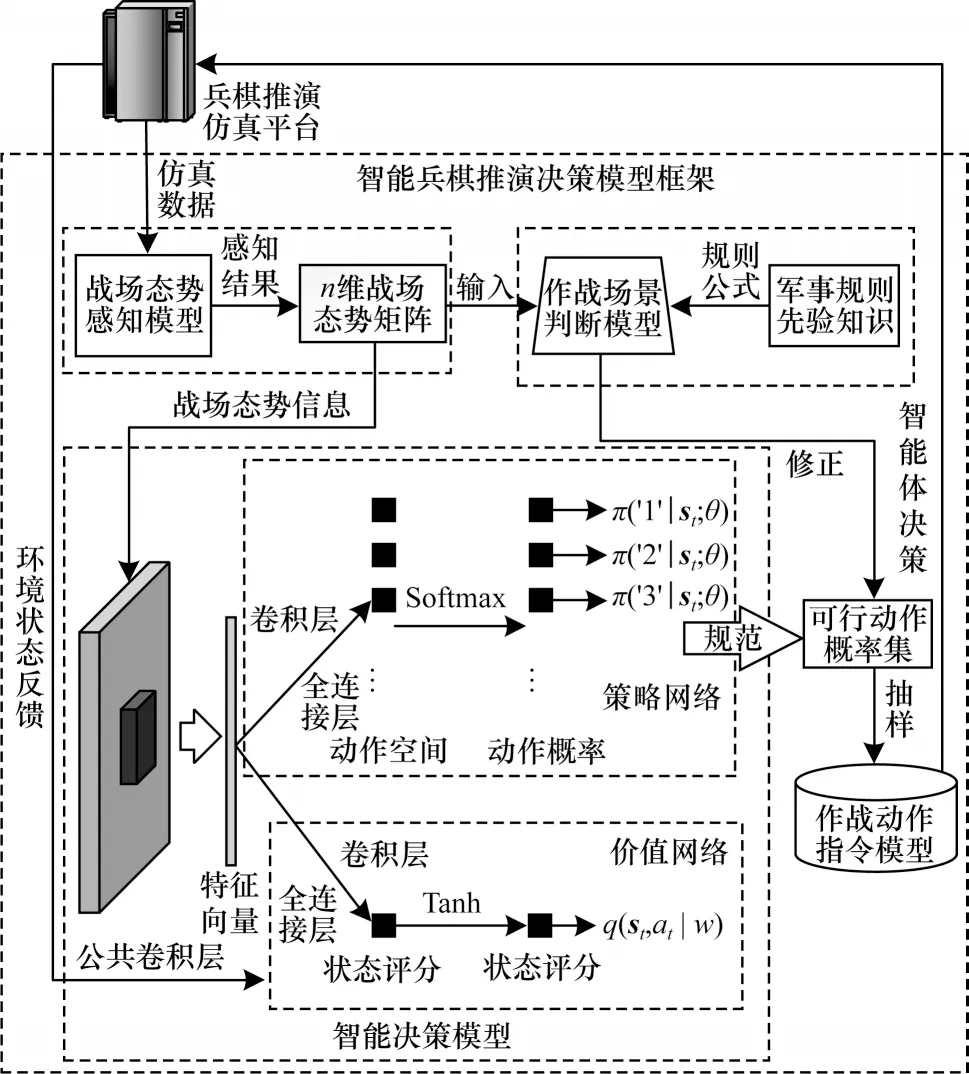
图1 基于深度强化学习的智能兵棋推演决策框架Fig.1 Framework of intelligent wargame deduction decision based on deep reinforcement learning

战场态势感知模型将兵棋推演仿真平台获取到的战场仿真数据构建为智能体所能感知的战场环境状态st，并将其作为作战场景判断模型和智能决策模型的输入。文献［18］介绍在兵棋博弈中指挥决策或行为的优劣评估，难以通过人为设计的奖励函数来判断，因此，基于军事规则先验知识指导智能决策模型最终策略的产出。智能决策模型将收到的战场态势信息，经公共卷积层进行态势感知，并提取特征向量，再分别发送给策略网络和价值网络。策略网络根据收到的特征信息输出当前战场状态下所有动作概率，得到可行动作概率集；价值网络根据收到的特征信息输出对当前战场状态st执行动作at的评分，并接收兵棋推演仿真平台的战场状态环境反馈信息。作战动作指令模型将获取到的智能体动作指令下达到兵棋推演仿真平台。该框架实现了智能体从战场态势感知、作战场景判断、智能决策产出以及最后的指令下达。

2.1 战场态势感知

战场态势感知用于帮助智能体构建状态空间，主要包含战场地图信息、棋子信息、作战场景规则信息等。其中，战场地图信息为智能体提供所处战场环境的视野，帮助智能体理解其战场作战环境与作战任务，棋子信息为智能体提供所拥有的作战兵力，帮助智能体判断其力量编组与作战目标，作战场景规则信息将为智能体提供指令规则，帮助智能体识别其作战指令决策来源，理解作战指令下达的合理性。文献［19］介绍实时感知并准确理解战场态势，挖掘复杂态势中的隐藏信息，是指挥员做出正确决策规划的基础。

本文提出兵棋智能体对于战场环境的感知方法，通过划分不同的战场要素实体，将智能体所获得的大规模战场初始信息数据进行分类与提取，以得到战场要素结果，并构造为智能体的输入矩阵，有助于智能体进行战场感知。

2.2 策略梯度中基准线的引入

兵棋智能体策略网络受兵棋推演对抗问题中较复杂因素的影响，存在策略产出较慢且训练效率较低的问题，而策略梯度算法可以帮助策略网络更新其网络参数。因此，本文在随机策略梯度中引入基准线（Baseline）进行改进，以提高策略网络训练效率。

文献［20］将Baseline 定义为1 个不依赖动作A的函数b。与传统策略梯度更新方式不同，若向策略梯度中加入Baseline，在期望不变的情况下减小策略梯度的方差，使策略网络的收敛速度加快。在策略梯度中引入函数b，则：

策略函数π为概率密度函数。式（8）中关于a求和后结果为1，因此式（8）结果为0，引入Baseline 的策略梯度将保证期望不变，即：

由于直接求策略梯度中的期望代价较高，因此利用蒙特卡洛对期望求近似值。在t时刻智能体通过随机抽样采取的动作为at～π(∙|st；θ)，令：

其中：g(at)为策略梯度的无偏估计。由于at是通过随机抽样得到的，因此随机梯度可得：

文献［21］介绍了若b的选择越接近于Qπ，则随机策略梯度g(at)的方差越小，策略网络训练时收敛速度越快。

2.3 策略网络的改进

由于在兵棋推演中战场状态st先于兵棋指令A被观测，而且不依赖于A，因此状态-价值函数Vπ(st)的评估结果只与当前战场状态有关。Vπ(st)定义如下：

Vπ(st)反映在当前状态下采取任何行动的预期回报，非常接近Qπ，需要的计算成本和参数量较少，较容易实现和调整。因此，在策略网络更新时引入Vπ(st)作为Baseline，在策略网络更新时，随机策略梯度方差会很小，能够提高策略网络在训练时的稳定性。由于Baseline 的引入提供了1 个较好的起点和参考点，因此会加快策略网络的收敛速度。此时的随机梯度计算式如下：

其中：动作-价值函数Qπ由Reinforce 方法近似得到。本文根据优先经验回放池［22］中的数据可计算得到Qπ的近似值ut。状态-价值函数Vπ(S)根据式（1）使用另一个卷积神经网络V(S；w)近似。随机梯度可近似：

状态-价值网络参数更新：因为动作-价值函数Vπ是对回报Ut的期望，因此可用Reinforce 方法观测到的折扣回报ut拟合Qπ得到预测误差。预测误差的计算式如下：

梯度下降更新状态-价值网络中参数ω，参数ω的计算式如下：

其中：γ为学习率。

此外，算法2 所示为引入Baseline 的策略网络参数更新方法。战场状态st和策略网络参数θt作为输入，下一时刻的策略网络参数θt+1作为输出，步骤主要有：

1）从at～π(⋅|st；θ)采样，得到动作at；

2）近似qt，qt≈Qπ(st，at)；

3）近似策略梯度g(at；θ)：

4）策略网络参数θt通过梯度上升更新，β是学习率，θt+1的计算式如下：

5）根据4）计算结果得到下一时刻策略网络参数θt+1。

随着策略网络训练加深，引入的Baseline 函数b会越来越接近动作-价值函数Qπ，在后续训练时收敛速度会不断加快。

2.4 低优势策略-价值网络模型训练框架

低优势策略-价值网络基于策略-价值网络，其低优势来源于优势函数。优势函数定义如下：

优势函数表示在状态S下，某动作a相对于平均而言的优势性。在本文优势函数恰好存在于式（13）中，若A(S,a)的值越小，说明该动作具有平均性。在策略网络中表现的随机梯度方差越小，这种低优势性将加快模型训练速度。

低优势策略-价值网络训练框架如图2 所示。

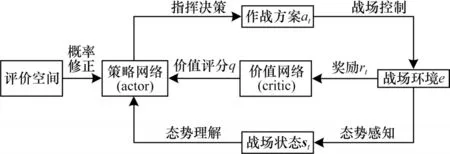
图2 低优势策略-价值网络训练框架Fig.2 Training framework of low advantage policy-value network

策略网络将给出当前战场状态st下的1 个经评价空间修正后自认为较优的作战方案at，经战场控制执行。价值网络为策略网络给出的动作at评分值q。策略网络根据q不断改进自身策略（更新w）以迎合价值网络判断，并结合低优势性，加快策略网络的收敛速度，战场环境给出的奖励rt不断提高价值网络评分的专业性和准确性（更新θ），使价值网络的打分更加合理。

2.5 低优势策略-价值网络的构建

在策略网络和价值网络中将当前战场状态提取为特征向量，因此在特征提取时可共用卷积层与池化层。输入信息首先经过3 层全卷积网络，分别使用32、64、128 个3×3 的过滤器，设置为ReLU 激活函数，以避免神经元节点输出恒为0 的问题，缓解了梯度消失问题。公共卷积层将提取到的特征向量分别输入到策略网络和价值网络。

公共卷积层通过共享权重增加效率和泛化能力，经过3 层全卷积网络所提取的特征向量后，包含战场环境的局部特征，如地形的边缘、地形类别等，还包括战场的全局特征，如战场布局与比例等。这些信息有助于策略网络生成合理的动作概率集，如根据地形类别特征帮助机动决策规划，根据战场布局特征帮助寻找合理的直瞄打击位置。

对于策略网络，设置4 个1×1 的过滤器进行降维处理，再接1 个全连接层，使用Softmax 激活函数对输出信息进行归一化处理，输出兵棋的可行动作概率，供智能体AI 进行动作选择。

对于价值网络，设置4 个1×1 的过滤器进行降维处理，再设置1 个具有64 个神经元的全连接层，最后再接1 个使用Tanh 激活函数的全连接层，将输出信息约束到[-1,1]之间作为战场状态好坏的评分。

本文的价值网络是对状态-价值函数Vπ的近似，而非传统动作-价值函数Qπ的近似。价值网络与策略网络都设置了过滤器进行降维处理，从而将输入的高维状态矩阵降维到1 个较低维度的特征空间。这种降维操作可能会丢失输入状态矩阵中的某些特征信息，导致在计算过程时出现偏差。若降维操作过于强烈，可能会导致神经网络在训练时出现欠拟合现象。但是，降维操作可以大幅降低神经网络的计算量，有效减少神经网络的参数量并缩短计算时间，提高神经网络的训练效率，通过降低输入矩阵维度，从而降低神经网络的复杂度，进而减少神经网络在训练过程中出现过拟合的风险。本文在实验中不断调整过滤器数量，以选择适当的降维策略，最终将过滤器数量设置为4，使神经网络在保证准确性、计算效率和泛化能力的同时降低过拟合出现概率。

智能体状态空间由4 个二值矩阵和1 个多值矩阵描述，并作为输入信息输入到低优势策略-价值网络中。低优势策略-价值网络的输入矩阵如图3所示。

图3 低优势策略-价值网络的输入矩阵Fig.3 Input matrix of low advantage policy-value network

根据战场态势感知信息，分别构造地形矩阵、兵棋位置矩阵（我方兵棋位置矩阵和敌方兵棋位置矩阵）、敌方上一步矩阵、是否为先手矩阵。

地形矩阵反映地图上每个位置的地形类型，如平坦地、山地、滩涂等。地形可以影响部队的机动速度、隐蔽性、攻击防御力等方面，对作战有着非常重要的影响。

兵棋位置矩阵记录了每个兵棋在地图上的位置，由于兵棋的种类、数量、位置等都会对作战结果产生重要影响，因此加入位置矩阵可直接反映兵棋位置，间接反映兵棋数量。策略网络通过兵棋位置矩阵可以更充分了解战场上的兵棋分布情况，从而制定更加合理的战术。在本文中，我方兵棋位置矩阵描述当前己方部队以及友军的情况。敌方兵棋位置矩阵描述敌方部队情况。

敌方上一步矩阵记录了上一个动作对应的状态矩阵，策略网络通过上一步矩阵可充分了解到战场状态的变化情况，从而更准确预测下一步可能的变化趋势，有助于策略网络学习作战的规则和战术。在本文中，敌方上一步矩阵描述敌方情况。

是否为先手矩阵记录了当前局面是先手还是后手，该因素对作战对抗的胜负非常重要。先手可率先展开攻势，占据更有利的位置。因此，是否为先手矩阵的加入是有必要的。

这4 类矩阵的加入使神经网络更全面地了解战场状态和作战规则，从而更准确预测下一步决策，制定更加合理的战术。

策略网络和价值网络的公共卷积层将从输入信息中提取棋盘状态的特征形成特征向量，将特征向量分别交给策略网络和价值网络进行后续处理。策略网络输出对于当前战场状态下每个动作的概率，供兵棋AI 参考动作选择。价值网络输出当前战场状态对于兵棋AI的好坏，供策略网络训练和博弈时参考。

3 实验与结果分析

3.1 实验环境与兵棋作战环境定义

本实验平台硬件配置使用移动版的NVIDA GeForce RTX3070 Ti显卡，Python 编程语 言被用 于软件配置上，具体的软硬件配置如表1 所示。

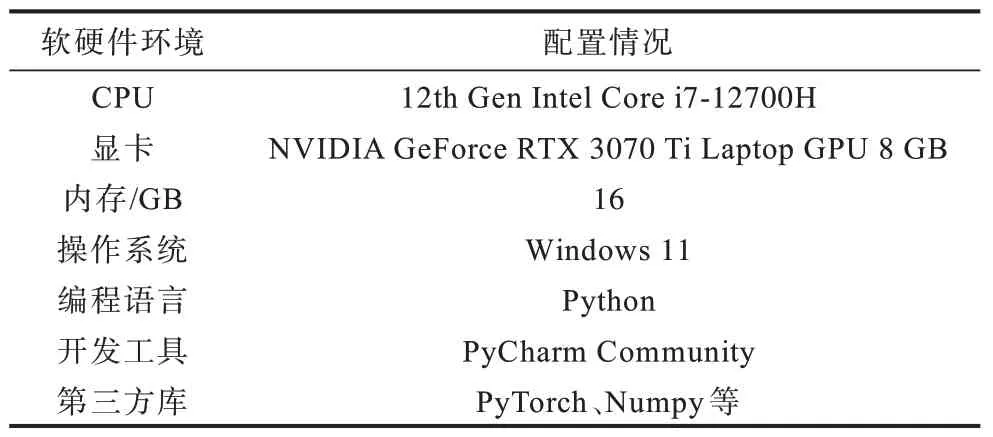
表1 实验配置软硬件信息 Table 1 Experimental configuration software and hardware information

为研究当前算法的可行性，本文设置一种具有代表性的作战场景，红蓝双方围绕岛屿夺控进行兵棋推演，场景设计示意图如图4 所示。

战场环境大小为16×16，以六角格坐标量化棋盘，这种六角格结构使得相邻的六角格之间可以沿6 个方向进行机动。从六角格的对称性分析，在计算时其中心点到6 条边的距离是相等的，并将距离设定为100 m。六角格可以更贴近实际作战环境，适应不规则形状和不同大小的场景，如凹型与凸型环境。该场景主要包含水面、滩涂、平地和植被4 类地形。六角格战场环境参数说明如表2 所示。

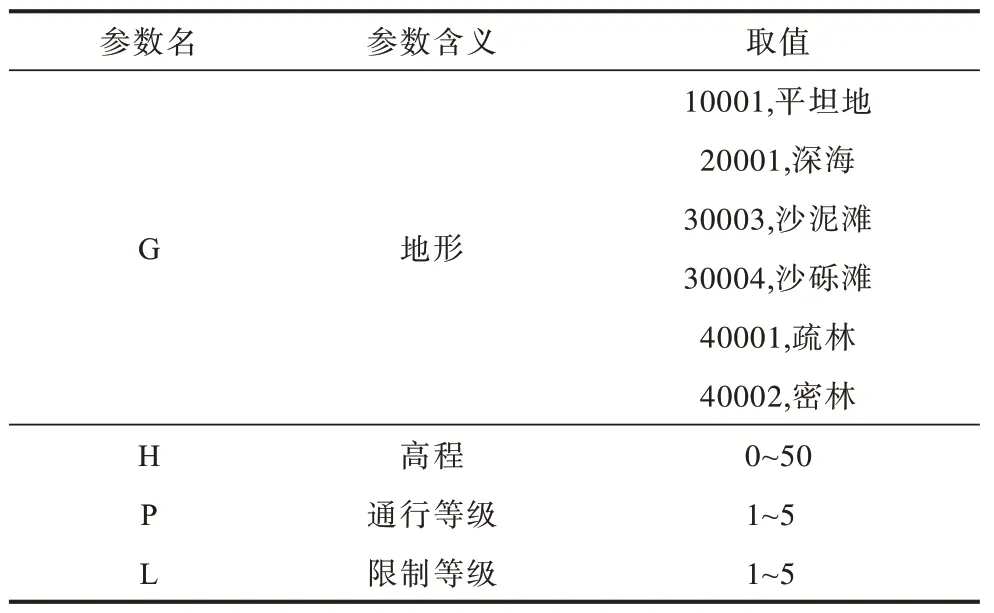
表2 六角格战场环境参数 Table 2 Parameters of hexagonal grid battlefield environmental

六角格战场环境的地形决定其通行等级与限制等级的数值，数值越高，通行难度越大。地形与通行等级和限制等级的关系如表3 所示。

表3 地形与通行等级和限制等级的关系 Table 3 Relationship between terrain and passability levels and restriction levels

平坦地与疏林的限制等级与通行等级都为1，对机动值的消耗最少。沙泥滩、沙砾滩和密林的限制等级为1，通行等级为2，对机动值消耗较高。在只有为平坦地和疏林的战场环境中，兵棋1 个回合最多能走4 格，而在沙泥滩、沙砾滩、密林等这类地形中，最多能走2 格。深海的限制等级与通行等级最高，兵棋一般是无法进行机动的。

高程变化从0～50，每增加1，平均海拔高度增加10 m，红蓝双方的所有棋子在该场景内对抗。本文实验所设定的主要战役规则如下：

1）战役最终胜利目标为歼灭敌方单位，双方初始血量为100，任意一方数量归零则战役结束，表明另一方夺控了岛屿。

2）在每次迭代开始时，红蓝棋子的初始位置在岛屿中随机产生，且不会出现在彼此射程之内，以增加战役的随机性，使得每次战斗都具有一定的不确定性，智能体需要灵活应对。

3）双方拥有相同的武器装备，当执行射击直瞄时，按距离增加造成的伤害逐步减小，直至超出射程无法射击。当执行射击间瞄时，通过贝塔分布进行伤害修正，以模拟现实中的射击情况，智能体在射击时对距离和瞄准进行权衡，以达到最佳的战术效果。

4）该场景中兵棋自身观测范围是有限的，同时高程差与地形也会影响射击通视情况，可能无法准确命中目标。为模拟现实中复杂的战场环境，智能体通过观测和推理来确定目标位置和可行的决策方案，以便更好地应对战斗情况。

5）六角格间高程差与地形的限制等级会影响棋子能否机动进入该六角格，地形的通行等级会影响棋子的机动性能。为模拟地形的复杂性和机动力的不同，智能体需要根据环境状态矩阵中包含的地形信息和自身状态进行合理移动决策，以便更好地适应战斗环境并实现作战目标。

该作战规则的实际性较高，歼灭敌方单位也是一种常见的胜利目标，双方初始血量为100 也能够反映兵棋在战斗中的真实受损情况与作战时的持久性。同时，兵棋初始位置的随机性能增加战术的多样性。武器装备产生的伤害按距离增加逐渐减小也符合实际射击的物理规律，而间瞄时按贝塔分布进行伤害修正也能更全面地考虑移动射击时对于打击精度的影响。在实际作战中六角格间的高程差和地形对机动进入该六角格的限制也是需要考虑的因素之一。同时，该规则较为简单，不涉及复杂的战术和策略，易于理解和操作，因此具有一定的普适性。除此之外，在一些实际战斗中需要考虑兵棋有限的观测范围以及地形对通视情况的影响，因此，这些规则应用于不同的战场环境中，例如城市、丛林、沙漠等不同类型的地形。但是，该规则也存在一定的局限性，由于不同类型的战斗可能存在其他不同的胜利目标，因此需要根据实际情况进行调整。

该推演实验博弈过程、规则和胜负标准具有一定的代表性，并且在实验验证过程和方法对比上有利于分析与验证。

3.2 实验结果

本文对该低优势策略-价值网络模型和文献［23］所提的传统策略-价值网络模型运用于兵棋问题环境中并进行训练，训练效果对比如图5所示。

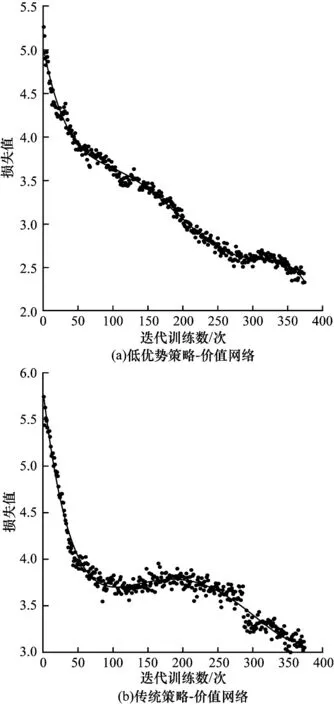
图5 低优势策略-价值网络和传统策略-价值网络的损失值下降趋势Fig.5 Decrease trend of loss values between low advantage policy-value network and traditional policy-value network

从图5 可以看出，在400 次自博弈对抗训练中，2 种模型的损失函数总体呈下降趋势。低优势策略-价值网络损失值从开始的5.3 下降到2.3，并且在前300 次迭代训练中，损失值下降较快，之后下降的趋势比较平缓。传统策略-价值网络的损失值从5.7 下降至3.0，并且在前100 次迭代训练中，损失值下降较快，在100～250 次迭代训练中下降趋势较为平缓，之后下降较快。因此，引入Baseline 的低优势策略-价值网络模型损失值下降的趋势与效果都优于传统策略-价值网络模型。

为评估低优势策略-价值网络模型对真实策略的拟合度，本文引入文献［24］所提的KL 散度进行评测，KL 散度趋势如图6 所示。

图6 KL 散度趋势Fig.6 Trend of KL divergence

从图6 可以看出，低优势策略-价值网络模型进行400 次迭代训练，KL 散度在刚开始训练时比较振荡。随着迭代训练次数的增加，KL 散度值越来越平稳，并且非常接近于0，说明低优势策略-价值网络模型的拟合策略近似其真实策略，在该实验场景中能得到最优策略。

在进行博弈训练时，本文将蒙特卡洛树搜索算法（MCTS）［25-26］作为对抗方参与同低优势策略-价值网络模型的训练。当低优势策略-价值网络模型迭代训练达50 次后，与MCTS 进行博弈评估，进行10 局对抗，并将定义的胜负率作为评估标准。胜负率的定义如下：

其中：wwin为低优势策略-价值网络模型的场数；ttie为平局数。表4 所示为在400 次迭代过程中MCTS 胜负率的变化，开始时MCTS 的搜索深度为1 000。MCTS 的胜负率变化趋势如图7 所示。

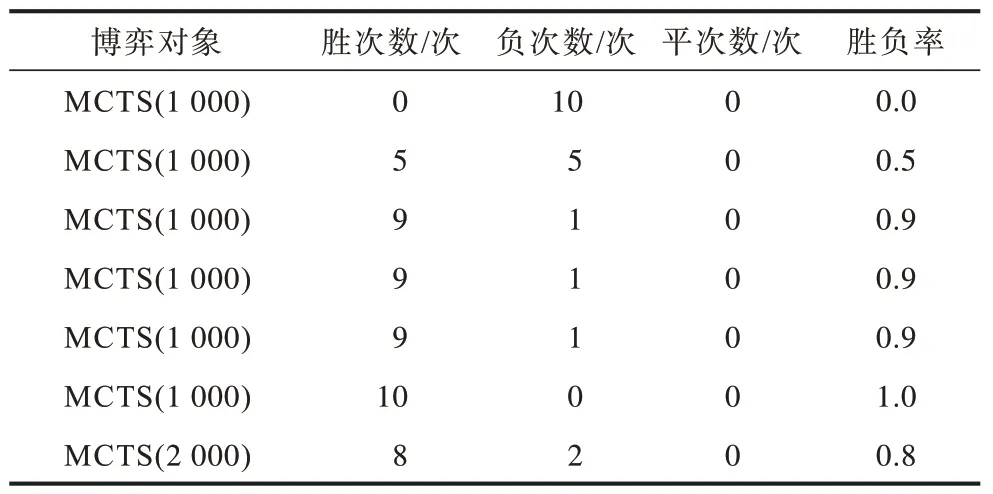
表4 MCTS 的胜负率变化 Table 4 Changes in win-loss ratio of MCTS

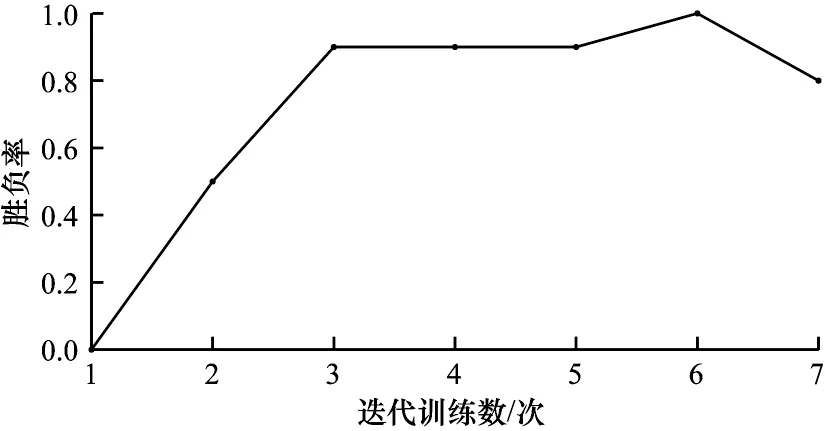
图7 MCTS 的胜负率变化趋势Fig.7 Change trend of win-loss ratio of MCTS

在每50 次迭代训练的对弈中，若低优势策略-价值网络模型10 局完胜时，MCTS 算法的搜索深度将增加1 000，在提高其指挥决策能力的同时保存算法模型的参数。图7 所示为进行7 次模型评估，在第6 次对抗MCTS 算法获取完胜后，本文将MCTS 的搜索深度提高到2 000，第7 次对抗仅负2 局，说明在此迭代阶段，模型已初步具备人类指挥员的作战能力。

为进一步验证LAPVN 决策的合理性，本文将训练好的LAPVN 智能决策模型与文献［27］所提的基于博弈树搜索算法中极大值-极小值（Max-Min）、α-β剪枝搜索算法以及搜索深度为3 000 的MCTS算法分别进行50 局对抗。由于博弈树搜索算法适用于对称性博弈，因此本文在此处的对比实验进行修改，将作战场景规则4）中兵棋的局部观测修改为全局性观测，以式（19）的胜负率作为对比指标，实验结果如图8 所示。

图8 不同网络的博弈对抗Fig.8 Game adversaries among different networks

从图8（a）和图8（b）可以看出，在兵棋推演对抗中LAPVN 的决策较为合理，博弈对抗时间也较短，同时从图8（c）可以看出，LAPVN 与博弈树搜索算法中2 类算法的胜负率在0.7 以上，对抗MCTS 算法的胜负比超过了0.7。

4 结束语

本文提出基于深度强化学习的智能兵棋推演决策方法。在策略梯度中引入状态-价值函数，实现对策略网络的改进。在理论推导与兵棋推演上的实验结果表明，在策略网络更新时将状态-价值函数作为Baseline，加快模型训练时的收敛速度，策略网络对于真实策略函数的拟合程度也非常接近。随着迭代训练的加深，该算法与MCTS 算法的对抗表现更优的决策水平。下一步将对如何提高Baseline 中动作-价值函数的拟合效率进行研究，实现对价值网络的改进与优化。