基于粒子群优化的差分隐私深度学习模型
2023-09-18张攀峰吴丹华董明刚
张攀峰,吴丹华,董明刚
(1.桂林理工大学 信息科学与工程学院,广西 桂林 541006;2.广西嵌入式技术与智能系统重点实验室,广西 桂林 541006)
0 概述
人工智能与大数据的联合应用模式近年来得到研究人员广泛关注,然而在人工智能与大数据技术快速迭代的同时,相关数据的隐私安全问题也日益严重。由于隐私泄露引发的社会风险层出不穷,在既保证数据的持续有效性又保护用户隐私不被披露的前提下,从海量数据共享问题中找到一种通用的交互方案尤为重要。差分隐私(Differential Privacy,DP)作为一种具有理论安全基础的数学模型,不仅可以直接应用于数据隐私保护,而且还能在人工智能深度学习领域提高模型的安全性,保护训练数据的隐私安全。
差分隐私可以被应用于推荐系统[1]、网络踪迹分析、运输信息保护[2]、搜索日志保护等领域。苹果公司使用本地化差分隐私手段来保护iOS 和MacOS 系统的用户隐私,并将该技术应用于Emoji、QuickType 输入建议、查找提示等领域,如使用CMS算法帮助其获得最受欢迎的Emoji 表情用来进一步提升Emoji 使用的用户体验。苹果公司要求应用商店中上线的应用都必须增加“隐私标签”,以符合“应用跟踪透明度”功能的要求。谷歌公司运用该项技术开发出隐私沙盒,允许广告客户展示有针对性的广告,但不会直接访问用户个人的详细信息。
此外,区块链技术、联邦学习等也可与该隐私手段相结合。例如,随着区块链的不断应用,环签名可以隐藏交易发起方,但不能保护区块链存储的数据,因此区块链的数据保护也可通过满足差分隐私得以保护[3]。联邦学习技术将来自不同隔离状态的数据尽可能统一,打破了数据孤岛障碍。同时,用户可以在不暴露原始数据的情况下参与深度学习,既能实现高质量模型的训练,又能保护隐私[4],因此差分隐私联邦学习能进一步预防攻击者从共享参数中推理出敏感信息。建设理想的人工智能世界需要数据、模型学习模式和智能算法,在这些需求下用户的隐私保护非常重要,基于差分隐私的保护技术已逐渐渗透到各个行业,成为除匿名、聚类、图修改[5-6]外的又一重要的隐私保护手段。
然而,在算法模型中引入差分隐私机制后数据的可用性可能会下降,权衡算法高效性和隐私保护程度仍然是研究该领域的难题。为此,本文结合算法模型在训练过程中的特点,对扰动后的参数进行优化,提出一种基于粒子群优化(Particle Swarm Optimization,PSO)算法的差分隐私模型训练方案,对网络中的梯度进行隐私保护,防止模型攻击中窃取的参数造成用户数据泄露。最后在集中式和联邦学习架构上进行训练和验证,防止数据的效用缺失。
1 相关工作
ABADI 等[7]将深度学习方法与差分隐私机制相结合,针对非凸优化且包含大量参数的复杂神经网络中隐私损失较大的问题,提出运用DP-SGD 算法计算训练模型。此外,通过高阶矩追踪隐私损失的详细信息,分析差分隐私框架下的隐私成本,提高隐私计算效率。该算法的提出为差分隐私深度模型训练在收敛性[8-9]、隐私分析、剪裁阈值[10-12]、超参数选择[13-15]等研究奠定了基础。然而,随着模型的加深和迭代次数的积累,噪声也会相应变大。为解决上述问题,YU 等[16]提出一种GEP 算法,将模型梯度映射到一个低维的锚子空间后再做扰动,绕开了维度依赖,并用辅助数据估计一个锚子空间,将敏感梯度映射到锚子空间中,得到一个低维的嵌入梯度和一个满足最小范数的残差梯度,分别在嵌入的梯度及残差梯度中添加噪声进行干扰,保证一定的差分隐私预算,由此实现比原来的梯度干扰低得多的扰动,且能保证相同的隐私水平。随后文献[17]提出一种基于重参数化的RGP 算法,通过两个低维的梯度载流子矩阵和一个残差权重矩阵对每个参数矩阵进行参数化,以近似的方式将投影梯度逼近原始梯度,对梯度-载波矩阵上的梯度进行扰动,并从有噪声的梯度中更新原始权重,但该方法在每一轮网络训练中都需要两个参数矩阵的参与,提高了网络计算的复杂度,对算力的需求较高,且投影梯度的方法忽略了参数结构的内在几何,阻碍经验风险的最小化。
许多主流差分隐私深度学习算法都是对计算过程扰动的优化,文献[18]通过对梯度进行编码,将其映射到更小的梯度空间进行扰动,并把梯度编码到一个有限的向量空间,使用数值技术来获得给定噪声分布的差分隐私边界以确定更好的效用-隐私权衡。DPTTAE 算法[19]使用一个更精确的近似张量打破高维参数矩阵约束,并利用差分隐私提供一个有保证的隐私和张量序列来压缩权重张量。YANG等[20]在DP-SGD 算法中对每个样本进行剪裁和归一化后,再添加噪声来模糊原始梯度信息,在DPNSGD 中引入一个正则因子以控制加速收敛,相应地实现了偏差和噪声权衡。文献[21]通过黎曼流提出一个黎曼优化框架,向遵循黎曼度量的切线空间黎曼梯度添加噪声,实现了经验风险最小化函数的差分隐私。梯度包含了数据集的相关信息,在进行参数更新之前的梯度中添加噪声,即对用户的数据进行扰动,可以保证最终的输出是被扰动过的。梯度扰动依赖期望曲率使之成为差分隐私深度学习的有效算法[8],在梯度扰动算法中加入的噪声和优化算法会相互影响,噪声会使优化算法避开最优曲率方向,而优化算法的收缩性则可以弱化之前步骤所添加的噪声。
噪声对模型依赖性较小,而添加的噪声会与模型规模成正比,从而影响算法性能,因此在前沿深度网络中仍存在巨大挑战。本文算法是对计算过程进行扰动,与梯度空间分析转换不同,根据模型训练的特有传播属性,使其自学习出每一轮满足隐私的最优权重,减少了权重参数化后对几何空间表述能力的依赖,且在保护隐私的同时仍具有较好的效用。
由于上述工作均采用模型训练时扰动的方式满足差分隐私,本文在多个数据集上进行了实验,并在实验过程中选择较为典型的算法进行对比,对简单的单通道数据集Mnist 和Fashion Mnist 采用2 种对比算法,对更为复杂的数据集Cifar-10 采用4 种算法进行对比。最后,将本文算法在联邦学习模式下进行验证和评估。
本文主要贡献如下:
1)提出一种基于PSO 的噪声参数优化方法,通过随机寻优或自适应寻优方案决定每一轮网络的初始权重,利用网络模型中参数的前向和反向传播特点,找到每一轮引入随机化后的最优参数,以提高模型的最终输出性能。
2)将网络每一轮训练时的初始化参数设为当前带扰动的最优参数,且在联邦学习客户端中使用同样的参数优化策略,使每个参与训练的客户端最终返回带扰动的本地最优参数,中心服务器聚合的参数也为当前最优。
3)相较其他复杂的参数提取、分解和重构等方案,基于PSO 的参数优化方式更加便捷,处理速度更快。
2 预备知识
2.1 差分隐私
差分隐私作为一种模糊查询工具,使得个人用户在数据集中对结果影响非常微小。在需要预防泄露的查询上添加噪声,并将其查询操作返回的实际结果隐藏起来或者模糊化,直至无法区分,从而实现私人数据的保护。差分隐私定义如下[22]:
对于差别为一条记录的数据集D和D',通过随机算法M 的输出结果为S子集的概率来满足差分隐私。隐私保护开销ε反映了隐私保护水平,ε越小,隐私保护水平越高,映射出关于数据集的有用的信息程度越深,但在相同情况下,ε越小,数据可用性越低。
差分隐私保护可以通过在查询函数的返回值中注入噪声来实现,但是噪声的大小相应地会影响数据的安全性和可用性。通常使用敏感性作为噪声大小的参数,表示删除数据集中某一记录对查询结果造成的影响。常用扰动通过拉普拉斯、高斯和指数机制来实现差分隐私保护。其中,拉普拉斯和高斯机制用于数值型结果的保护,指数机制用于离散型结果的保护。
在相同或不同数据库上可以重复使用差分隐私算法,其满足组合理论[23]。
定理1假设有n个随机算法M,当其中任意两个Mi的随机过程相互独立且满足εi-差分隐私,则{Mi}(1 ≤i≤n)组合后的算法满足εi-差分隐私。
定理2假设有n个随机算法M,当其中任意两个Mi的随机过程相互独立且满足εi-差分隐私,则{Mi}(1 ≤i≤n)组合后的算法也满足max(εi) -差分隐私。
2.2 神经网络模型
神经网络中每个节点表示一个感知器,模拟生物细胞网络中的电信号通过突触传递给神经元,当神经元收到的信号总和超过一定阈值后,细胞被激活,通过轴突向下一个神经元细胞发送电信号以加工完成外界传递的信息。常见的多层感知机包含一个输入输出层和多个隐藏层,所有层都采用全连接方式。卷积神经网络由可以处理多维数据的输入层、隐藏层和输出层构成,其中隐藏层一般包含卷积层、池化层和全连接层三类架构。卷积层的反向传播使用交叉相关计算,如式(2)所示:
其中:L 为风险管理误差;f′为激活函数导数;η为学习率。
ResNet[7]克服了训练深度增加导致的网络退化问题,并通过残差学习向上堆叠新层来建立更新网络,相比普通网络在卷积层之间增加了短路机制,使得对特征向量的学习发生改变。假设对输入x学习到的特征是H(x),残差是H(x)-x,原始的学习特征就变为F(x)+x,使得残差学习相比原始特征学习变得更容易。
2.3 粒子群优化算法
粒子群优化算法[24-25]的目标是使所有粒子在搜索空间中找到最优值。在初始化时,给空间中所有粒子分配初始随机位置和初始随机速度,根据每个粒子的速度、问题空间中已知的全局最优位置和粒子已知的个体位置依次迭代推进每个粒子的位置。随着计算的推移,通过探索和利用空间中已知的有利位置,粒子围绕一个或多个最优点聚合。在搜索过程中,保留全局最优位置和个体历史最优位置信息,有利于加快收敛速度,避免过早陷入局部最优解。
3 方案的设计与实现
3.1 基于PSO 的差分隐私方案
在深度学习中,模型通常需要基于观察数据x,x可以是输入数据或特征值,对应输出一个概率分布p(x;θ)。常见的优化算法是基于梯度的,模型训练的基本任务是优化如下的目标函数:
梯度扰动间接参与了参数的更新过程,保持既定方法会很大程度上影响参数收敛,使其在距离最优参数较远的位置来回振荡。随着参数权重的不断迭代,权重值会减小,而噪声规模占比增大,概率分布的方差也随之增大,最终导致模型过度拟合训练数据中的噪声。
考虑到差分隐私梯度扰动机制是在反向传播的梯度信息中加入随机噪声,这一过程会影响输出概率的期望,扩大神经网络最大似然估计参数的后验分布输出概率偏差和方差。本文提出一种基于粒子群优化(PSO)算法的参数寻优策略,目的是弥补因梯度脱敏造成的模型可用性下降的缺陷。如图 1 所示,在N个样本参数空间为ℝp×d的搜索空间中,假设N是粒子总数,每一个粒子都对应一个由目标函数决定的适应值。通过适应值找到当前情况下的最优解,即参数θi,将当前参数进行位置更新后作为每一轮网络前向传播的初始参数,根据更新后的目标函数反向求位置参数的梯度。为保证数据隐私安全,在梯度上进行剪裁并用噪声机制进行干扰,返回更新后的参数。每个粒子适应度值将用于判断该轮更新后的样本参数是否参与下一轮的训练,若该粒子适应度是当前最优,则更新参数样本空间,否则保留历史最优粒子样本空间。在迭代结束后,粒子群优化得到的参数为全局最优,且神经网络训练过程满足差分隐私。
鉴于上述思路,基于PSO 参数优化的差分隐私架构如算法1 所示,用粒子的位置表示网络中各神经元优化后的权重参数,目标是在有限迭代中找到粒子最优位置,即在隐私保护的前提下找到神经网络的最优参数。将网络的损失函数作为衡量粒子位置是否为最优的适应度函数。在网络训练过程中引入粒子群优化算法,在梯度下降的基础上,每一次粒子速度和粒子位置的更新,就是神经网络经历的一个训练轮次。
算法1基于PSO 的差分隐私网络

在迭代开始前,首先随机初始化粒子群中的位置p和速度v,然后初始化相应的个体历史最好位置Pp和群体最优位置Pa、个体历史最优值Vp和种群历史最优值Va,初始适应度值为零。在每一轮迭代中,首先确定速度变化vt和位置变化pt,一般情况下的速度成分由惯性项w×v、量化过去表现的认知部分c1×rand()×(perbest(pt) -pt)和量化邻居信息的社会部分c2×rand()×(allbest(pt) -pt)组成,速度vt决定了新位置的方向和大小,所以两者都为矢量。在分批训练中,将N个粒子的位置参数作为网络参数θt依次在网络中执行计算。计算过程使用随机梯度下降来最小化经验损失函数L(θ),即对每一批采样数据计算当前梯度∇θtL(θt,xi),对所得梯度进行剪裁防止梯度爆炸或消失,剪裁后的梯度表示为,每个样本梯度添加服从N(0,σ2C2I)的噪声来更新参数。梯度下降的步骤与传统的方法相同,但区别在于参加运算的参数已经是基于PSO 的当前最优,梯度也是基于当前参数得到的,更新过程能一直保证梯度隐私。根据得到的适应度值V,遍历N个粒子,若某粒子适应度分数小于个体历史最优值,则记下当前参数perbest(pt+1),更新出的个体最优粒子流入到下一轮继续更新。根据该轮种群最优位置选出最小得分的粒子,其对应的参数为当下全局最优粒子位置allbest(pt+1),即一轮结束后的网络新参数。
在新一轮训练开始前,采用惯性权重w、粒子位置p和粒子速度v等自定义参数更新每个粒子的速度和位置,本文中称为随机优化。若将每一次网络迭代后的参数作为调整方向和速度后的粒子矢量,称为自适应优化,则该情况下的w、p、v每一轮训练前都会动态改变,但实验中只需粒子矢量位置,无须对这些值做进一步定量研究。如此循环,达到停止条件时可得到一个满足差分隐私的模型和扰动后的最优参数,根据(ε,δ)可知隐私保护水平。
3.2 隐私参数修正分析
上述基于粒子群优化后的差分隐私网络,其目标函数如式(6)所示:
每一轮训练后,当前网络最优参数allbest(θi)的梯度为:
其中:allbest(θi)=PSO(θi),i∊(0,N),这里的函数表达式为显性连续函数,可直接微分得到梯度。
本文主要观察参数变化,故在梯度下降算法中,记ya fa(p(x;θ)) 为fa(θ),ya fa[p(x;allbest(θi))] 为fa(best(θ)),在不添加噪声的情况下,一般神经网络训练目标记为:
在实际应用中需要采用分批训练的方式,因为数据集样本数A≫B,每一次从训练集中随机抽样,然后进行梯度估计,即随机梯度下降(SGD)算法。本文假设批大小B=1,即每次取一个样本参数更新方程,表示如下:
应用粒子群优化策略后,随机梯度下降更新过程可以表示为:
记(best(θt)-θt)+η[∇f(best(θt))-∇f(θt)] 为ΔV(θt),则下降过程可表示为如下形式:
其中:{γt}为取值 在{1,2,…,A/B}上的独 立同分 布(Independent Identically Distribution,IID)随机变量。式(13)是对式(10)的修正结果,满足随机微分方程的弱近似。ΔV(θt)可以看作是在ℝp×d空间中的随机矢量,ΔV(θt)+f(θt) -fγt(θt)也为该d维空间中的随机矢量,最 终f(best(θt)) -fγt(best(θt))记为Vt,为d维随机矢量,显然Vt依赖于当前的best(θt)。由此可假设一个扩散过程来近似,考虑ΔV(θt)的均值和方差,显然均值为0,扩散系数为:
随机微分方程表达式为:
将式(15)连续过程离散化,迭代过程可以变体为如下形式:
其中:Zt~N(0,I),对照式(13),设置Δt=η,b~∇f,σ=,就可以得到式(15)这一连续过程的弱近似。
为使离散逼近连续,弱近似的定义如下:
定义1令0<η<1,A>0,且,G为多项式增长函数的集合,g∊G,即存在常数T,当t>0时,满足|g(θ)|
则称随机方程W是随机梯度下降的α阶近似。
若随机过程为Θt,对于t∊[0,T]满足:
则式(18)是随机梯度下降的一阶近似。
若随机过程为Θt,对于t∊[0,T]满足:
则式(19)是随机梯度下降的二阶近似。
因为式(11)是在原始参数θt上进行优化的,根据梯度修正后的连续函数,显然函数的期望和方差会更小,所以证实该隐私参数更新方法在理论上具有可行性。
3.3 隐私证明
神经网络经由一轮采样、梯度计算、梯度剪裁和添加高斯噪声组成的训练后,会得到一组满足(ε,δ) -DP 的参数θt,不同的是本文中的参数在粒子群算法优化后,best(θt)的值作为新的参数出现在下一轮的计算,这里传入的参数优于常规的梯度扰动更新方法,但不影响满足差分隐私。经过T轮训练后,模型收敛。
根据矩会计法[7]可以计算训练系统的总体隐私损失,其基本思想是将每一轮训练的隐私损失等价于随机变量,而将总隐私损失等价于各轮随机变量的和进行分布,通过计算随机变量的矩生成函数得到更精准的隐私上界。对于t时刻的训练机制Mt,差分隐私目标是让其在相邻数据集上得到的参数θt的分布尽量相似,即对所有的数据集d,d'∊D,满足:
可知t时刻的位置由t-1 时刻变化得到,采用随机梯度下降法在数据集上训练时,可定义随机变量如下:
其中:θi~Mt(PSO(θti-1),d),i∊(0,N),取每一轮得到的最优随机变量记为c(θi,Mti)。由组合定理[7,26]可知,对于T个差分隐私机制组成的训练系统,在不同t时刻输出的参数独立同分布,训练体系的总体机制M1:T的随机变量可由多个时刻的隐私随机变量的和组成,即考虑到相邻数据集的分布需要尽可能一致,则随机变量c(θi,Mti)的α阶矩估计应尽可能地逼近0。c(θi,Mti)的对数矩生成函数为:
故训练时整个模型满足差分隐私,隐私预算ε为TM(α)。
3.4 联邦学习中的PSO 差分隐私策略
联邦学习差分隐私模型采用局部噪声机制,对于每轮训练而言,当客户端更新完本地模型后,都需要将模型权重或者更新的梯度上传至中心服务器进行汇聚。实验中为满足本地差分隐私,采用剪裁操作和噪声干扰来对模型权重或梯度进行处理,然后上传至中心服务器。
本文方法采用聚合方式进行训练,客户端和服务器计算包含如下流程:在本地计算时,首先初始化寻优所需的粒子位置参数p0、速度参数v0、个体历史最优位置pp、全局最优位置pa、适应度值V、个体历史最优值Vp和当前所有粒子中的最优值Va。客户端k根据本地数据库Xk,将全局服务器模型授予的θt作为本地参数,即θ=θt,进行梯度剪裁和下降策略,采用粒子群最优算法更新参数。在客户端的每一轮训练过程中,根据适应度函数值V更新该轮的历史个体最优参数为perbest(pt),全局历史最优参数为allbest(pt)。该轮更新结束后,网络参数θt为当前最优,继续进入下一轮。客户端训练结束后,模型训练会将得到的参数Δθt+1←θ-θt、ξ←‖Δθt+1‖n传给服务器,其中n表示范数,此时上传的客户端参数是基于多轮PSO 优化后的最优参数。在模型扰动时,每个客户端产生一个符合高斯分布的随机噪声N(0,σ2C2I)。因此,经过扰 动的本 地参数为服务器使用FedAVG 算法[27]聚合从客户端收到的Δθ′t+1,得到新的全局模型参数θt+1,此时模型参数是扰动后的,符合差分隐私。然后当有客户端需要训练时会进行模型广播,服务器将新的模型参数广播给每个客户端。客户端接收新的模型参数重新进行本地计算,更新本地参数再扰动后回传到聚合中心。
算法2基于PSO 的差分联合策略

4 实验结果与分析
4.1 实验设置
实验基于Python3.8 解析器和PyTorch 框架,在3.30 GHz 3.29 GHz 双核CPU,128 GB RAM 的win10系统下,使用NVIDIA GeForce RTX 3090 GPU 实现加速。实验数据集使用Mnist、Fashion-Mnist 和Cifar-10,其中,Mnist 是标注为0~9 的手写数字图片数 据,Fashion-Mnist 由10 种衣物 类别组 成,2 个数据集的图片均为单通道,包含60 000 张训练图片和10 000 张测试图片。Cifar-10 由10 类真实物体的三通道彩色图组成,包含50 000 张训练图片和10 000 张测试图片。
训练模型包括自定义的MLP、CNN 和ResNet20网络。MLP 网络由包含300 个和100 个神经元的隐藏层构成,自定义CNN 网络包含两个通道数为32 和64 的卷积模块,卷积核大小都为3,步长设置为2,每个卷积层之后都使用ReLU 作为激活函数,输出采用10 分类的全连接层实现。ResNet20 由包含19 个核大小为3、步长为[1,2]、通道数为[16,32,64]的卷积层以及1 个全连接层构成。其中联邦学习差分隐私的测试分析在自定义CNN 网络上完成。
4.2 PSO 超参数分析
粒子群优化算法中各参数的选取对模型的表现至关重要,故在无隐私情况下讨论确定各PSO 超参数对模型的增益。由于粒子位置p、粒子速度v等参数与神经网络权重相辅相成,因此只讨论超参数粒子群数N、惯性权重w和最大迭代次数T对模型的影响。
当取不同粒子数N时,模型的准确率和训练时间如表1 所示,可知当粒子数为3 时,模型已经具有较好的表现,当粒子数为10 时,准确率提升很小,但时间却增加了4 倍,当粒子数取到20 时,耗时相对N=3 更长,但准确率提升较小。在进行不同粒子数下的模型训练时,迭代轮次都为100,惯性权重都设为0.1。

表1 本文模型在不同粒子数下的性能Table 1 Performance of the proposed model under different particle numbers
当惯性权重w变化时,模型的准确率如图2 所示,其中,训练迭代100 轮次,粒子数为3。在w=0.7时,模型准确率在15 轮左右开始骤降,猜测是在该权重下训练陷入局部最小导致。当权重为0.1~0.5时,模型收敛的速度增快,但最终都会收敛到相差不多的值域内。当w=0.9 时,在前10 轮的学习能力较强,但会因粒子速度更新跨度过大而提前进入局部最小,使得准确率相对较低。图3 所示为在不同最大迭代次数T下模型训练损失、准确率、测试损失和准确率的变化情况,其中,惯性权重为0.1,粒子数为3。随着最大迭代轮次的增加,训练和测试集的损失都有所降低,准确率都有所增加。当T超过200 轮后,损失逼近0,训练集完全收敛。测试集在100 轮后,损失收敛至0.1 附近,准确率也几乎不再变化。
4.3 结果分析
本文将基于粒子群优化的差分隐私模型训练方法在多个数据集和网络中进行实验,并与其他算法进行对比。实验中粒子种群数量设置为3,主要是根据实际训练经验、显存和时耗综合考量得到的。对比实验和结论均在控制变量的情况下得到,例如为了比较和探究隐私保护程度时保证隐私预算一致,对算法准确率和损失进行验证。根据DP-SGD[7]和RG-params[17]算法,实验中选取隐私预算ε为2、4、6、8 和10 进行讨论和对比。
为了观察PSO 的收敛特征和可行性,首先采用随机优化的方式对隐私参数进行训练,将训练过程中随迭代累计的测试集分类准确率与DP-SGD[7]、DPparams[28]算法对比。图4 所示为Mnist数据集在MLP模型上的实验结果。从曲率总体变化上可知,随着迭代次数的增加,基准的梯度扰动算法准确率会先增加后降低,随着隐私预算的收缩,降低幅度会越大,而本文方法的训练效果受隐私预算干扰较小,训练过程较平稳。图4(a)~图4(e)中的预算ε为10、8、6、4 和2,最终DP-SGD 测试准确率为84.43%、82.94%、80.71%、77.06% 和71.25%,本文算法最终测试集准确率为90.67%、90.33%、90.28%、90.78%和90.66%,而在基于输出扰动的DP-params[28]训练集损失一直都在较高水平,准确率也始终只有10%左右。
图5 所示为在简单CNN 网络上各算法测试结果与隐私水平的变化趋势,在图5(a)~图5(e)中,当ε为10、8、6、4 和2 时,DP-SGD[7]最终测 试准确率为84.58%、82.68%、79.87%、75.28%和67.52%,本文算法的损失最终收敛于0.55 附近,准确率可达87.81%、87.57%、88.19%、88.24% 和88.26%,而DP-params[28]的训练损失在该卷积网络中有所下降,准确率相较MLP 网络中有所提升,分别为66.63%、70.25%、64.30%、68.21%和69.63%。显然,本文算法在收敛和准确率上仍具有较大优势,但Mnist 数据集在两种网络框架中,当隐私预算ε为4 时,收敛前训练损失和测试分类准确率会出现较大波动,可能是在随机寻优时不能直接确定最优初始参数,当隐私政策紧缩时无法快速靠近最优位置造成的。
为验证算法的普适性,进一步对Fashion-Mnist数据集的损失值和测试准确率进行实验。图6(a)~图6(e)展示出Fashion-Mnist在MLP 网络结构中,当ε为10、8、6、4 和2 时的收敛情况和模型效果评估。算法DP-SGD[7]的最终训练集损失随隐私预算紧缩而急剧增大,在测试集上准确率为76.17%、74.92%、73.47%、71.40%和67.80%。相比之下,本文算法的损失值较为稳定,最终能收敛到1 左右的较小范围,准确率可达83.10%、83.31%、83.38%、83.49%和83.99%,而DP-params[28]损失函数值始终处于较高水平,最终测试准确率只有10%左右。从曲线变化趋势可知,DPSGD[7]在收敛到最优状态后,隐私预算越小,最终的模型效用越差。而在本文算法中,随着噪声的增加,从Fashion-Mnist 在MLP 模型上的表现可知,训练损失始终向风险最小趋势靠近,测试准确率偏差不大。
图7 所示为Fashion-Mnist 数据集在CNN 中的损失值和测试准确率表现。在图7(a)~图7(e)中,当隐私预算ε为10、8、6、4 和2 时,随着隐私预算的缩减,最终DP-SGD[7]的训练损失值涨幅较大,测试准确率为75.25%、75.00%、72.50%、69.37% 和64.13%。在Fashion-Mnist 数据集上,本文算法的最终损失函数值的表现最优,在测试集上准确率为80.44%、80.45%、80.41%、80.76%和81.40%。而DP-params[28]的损失一直徘徊在2.3 附近,测试准确率也始终在较低水平阈值内振荡。由图7(a)可知,当ε为10 时,本文算法的收敛速度、最终收敛程度和测试效果始终领先。当隐私保护程度越大时,其最终结果的优势越明显。
本文算法在Mnist 和Fashion-Mnist 上均能较好收敛,且在相同隐私预算下受噪声叠加扰动的影响较小。在不同的隐私预算下也有较优表现,能在不同数据集和不同神经网络架构上使模型都具有较好的鲁棒性。但考虑到随机寻优的方式收敛较慢,且对粒子参数的初始位置、寻优方向和速度的调整较为繁琐,在后续ResNet 架构中考虑采用网络自适应寻优的方式调整每一轮的方向和速度。
当采用更复杂的ResNet深度模型时,无差分隐私训练的Mnist 测试集准确率为99.43%,Fashion-Mnist数据集准确率为91.19%,彩色图像数据集Cifar-10 的准确率为79.64%。各数据集在不同隐私水平下的测试集准确率如表2 所示,其中,每列的隐私保护水平均一致,所有准确率由训练最佳的模型获得,每个结果为3 次模型训练的均值,Δ表示与基准测试准确率的偏差。将DP-SGD[7]算法作为扰动算法的基准线,可知梯度扰动后本文算法在3 个数据集的上的结果均为最优。Mnist 数据集在隐私损失为8 时,准确率可达98.44%,比基准线提升了5.03%。Fashion-Mnist在隐私损失为10 时,扰动后最高准确率为87.46%,比基准线提升了9.23%。在Cifar-10 数据集上,当隐私损失为8 时,最高准确率为66.7%,比DP-SGD 算法提升了22.77%。因此,本文算法在隐私预算和准确率指标上均优于其他训练方案。

表2 不同隐私水平下的测试集准确率 Table 2 Testset accuracy at different privacy levels %
根据RDP[29]隐私计算方法,采用更小的隐私预算,在Cifar-10 上基于ResNet 模型进行对比,最大迭代数为50 轮。表3 为较小隐私开销下各算法的测试集准确率,与文献[7,17]相同,设置DP-SGD 为基准线。RGP-W4 明显不具优势,甚至在隐私预算为1.0和0.1 时的表现低于基准线。GEP 和RGP-W10 仍优于DP-SGD,但显然本文算法对准确率的提升更稳定,在隐私预算为0.1 时,测试准确率有13.39%的提升。综合来看,无论在何种隐私水平下,本文算法均可更好地提升模型可用性。

表3 较小隐私水平下的测试集准确率 Table 3 Testset accuracy at smaller privacy levels %
此外,本文算法在算力需求和训练时间上也具有一定优势。由表4 可知,本文算法的每一轮训练需 要72 s,趋 近RGP[17]时耗的1/3,相 比RGP[17]和GEP[16]的高维参数或梯度的处理计算,本文算法则是利用自启发式寻优,避免过量运算。在本文实验环境下对GPU 的显存需求是8.2 GiB,优于前两者。

表4 不同算法的训练耗时和显存大小 Table 4 Training time and video memory size of different algorithms
4.4 联邦学习中的结果分析
考虑到多源海量数据整合问题,下面研究本文算法在联邦学习中的表现。不同于分布式机器学习将独立同分布(IID)的数据或模型参数存储在各个分布式节点上,本文方案由中心服务器调动数据和计算资源联合训练模型。因客户端的地理、时间等分布差异,联邦学习经常要处理非独立同分布(non-IID)的数据。因此,实验在不同数据集上采用IID 和non-IID 的方式分别进行训练,并观察算法在收敛性和隐私保护中的性能映射。
图8 所示为Mnist 在不同隐私水平下采用独立同分布训练的测试准确率变化过程,本文算法在隐私预算为10 时的准确率最高可达98.29%,隐私预算为2 时的准确率达到96.2%。图9 所示为该数据集在非独立同分布形式下的测试集收敛曲线,本文算法在隐私损失为10 时的准确率可达96.49%,损失预算为2 时的准确率为89.28%。可以看出每个参与训练的客户端数据相互独立时的准确率较高,从全局角度而言,本文算法的收敛速度均优于传统的直接差分隐私扰动算法。在相同隐私水平下,本文算法模型效用更佳,在隐私保护水平越高时优势越明显。
图10 所示为不同隐私预算下独立同分布形式的Fashion-Mnist 数据集在网络训练中的测试准确率,隐私损失为10 时的准确率为89.31%,隐私损失减小到2 时的最高准确率为86.19%。图11 所示为非独立同分布Fashion-Mnist 数据集在网络训练中的测试准确率,当隐私损失为10 时,本文算法最高准确率为83.76%,隐私损失为2 时的准确率为75.93%。由综合数据和曲线可知,在Fashion-Mnist 数据集中,IID 数据的训练效果仍然优于non-IID,且本文算法的收敛速度仍然较快,在独立同分布的数据中训练优势依旧明显,即使在non-IID 数据中的优势相比Mnist 有所下降,但仍然优于传统的噪声扰动方式。

图1 本文方案的参数优化策略Fig.1 Parameter optimization strategy of the proposed scheme
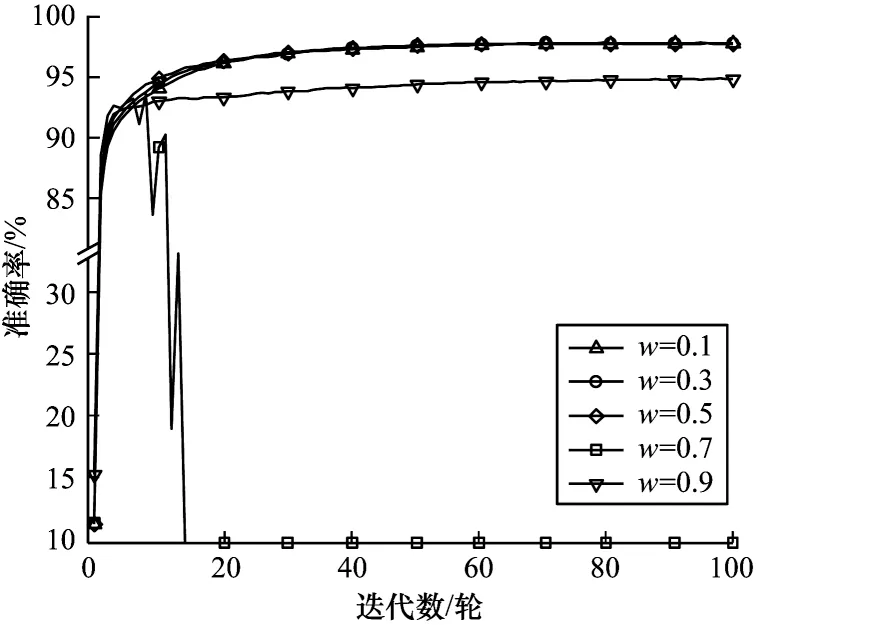
图2 本文模型在不同惯性权重下的准确率Fig.2 Accuracy of the proposed model under different inertia weights

图3 本文模型在不同迭代数下的准确率Fig.3 Accuracy of the proposed model under different iterations

图4 Mnist 数据集在MLP 网络中不同隐私水平下训练的测试准确率变化曲线Fig.4 Test accuracy variation curve of Mnist dataset trained under different privacy levels on the MLP network

图5 Mnist 数据集在CNN 网络中不同隐私水平下训练的测试准确率变化曲线Fig.5 Test accuracy variation curve of Mnist dataset trained under different privacy levels on the CNN network

图6 Fashion-Mnist 数据集在MLP 网络中不同隐私水平下训练的测试准确率变化曲线Fig.6 Test accuracy variation curve of Fashion-Mnist dataset trained under different privacy levels on the MLP network
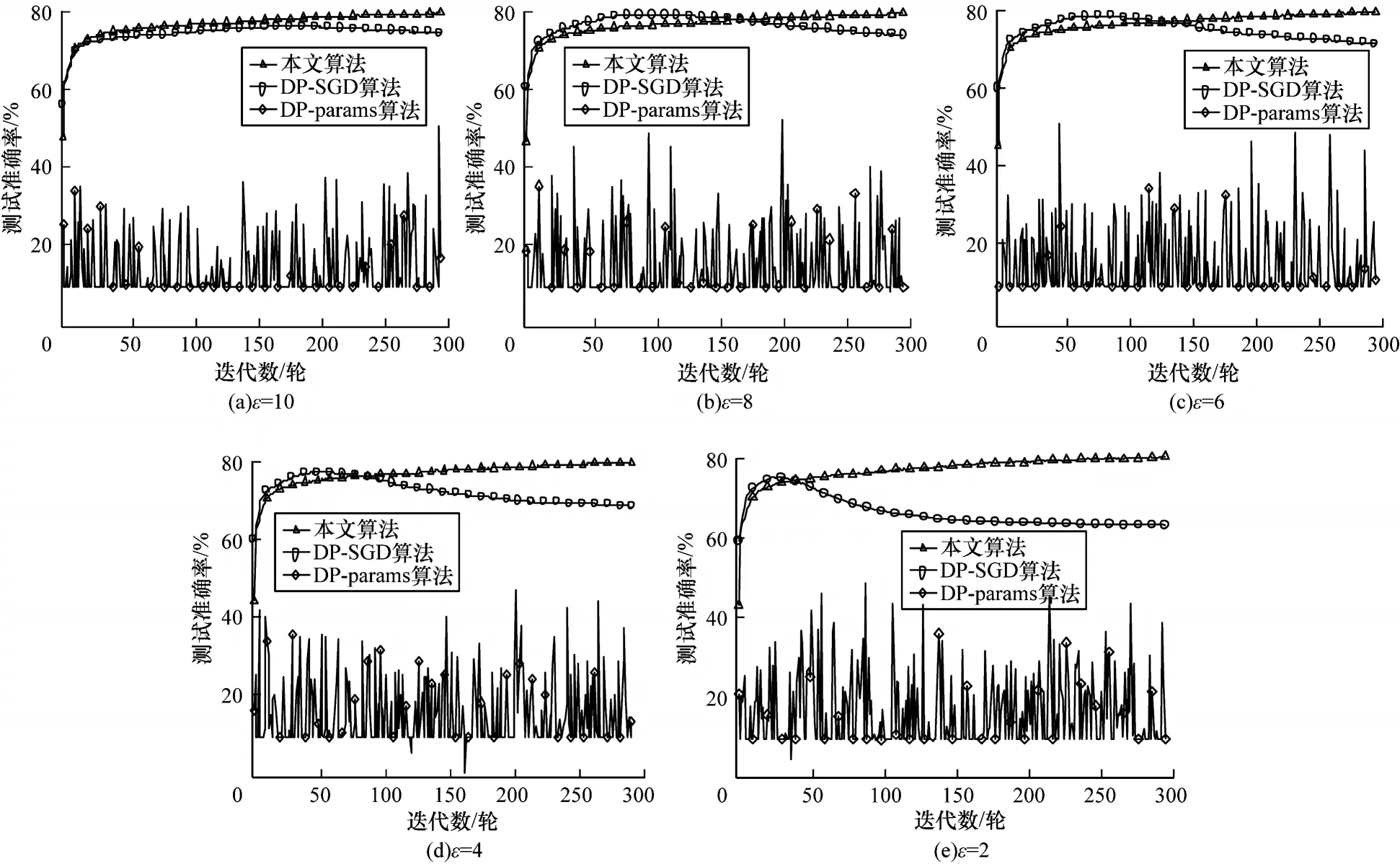
图7 Fashion-Mnist 数据集在CNN 网络中不同隐私水平下训练的测试准确率变化曲线Fig.7 Test accuracy variation of Fashion-Mnist dataset trained under different privacy levels on the CNN network

图8 不同算法在Mnist 数据集上的IID 测试准确率Fig.8 IID test accuracy of different algorithms on Mnist dataset

图9 不同算法在Mnist 数据集上的non-IID 测试准确率Fig.9 non-IID test accuracy of different algorithms on Mnist dataset

图10 不同算法在Fashion-Mnist 数据集上的IID 测试准确率Fig.10 IID test accuracy of different algorithms on Fashion-Mnist dataset

图11 不同算法在Fashion-Mnist 数据集上的non-IID 测试准确率Fig.11 non-IID test accuracy of different algorithms on Fashion-Mnist dataset
本文优化算法在联邦学习中具有较强的兼容性,收敛速度较快,并具有较好的隐私性和安全性,且在面对用户群体较大与不均衡的用户数据时,仍然具有较好的兼容效果。
5 结束语
本文构建一个基于粒子群优化的差分隐私深度学习模型。根据网络前向传播和反向传播中每轮参数的方向和速度变化特征,配合噪声扰动对期望曲率的依赖关系,解决噪声参数寻优问题。在训练过程中,基于每轮梯度扰动后的最优参数得到经验风险最小化函数,解决网络参数更新的逼近问题。在Mnist、Fashion-Mnist 两个单通道数据集和Cifar-10彩色多通道数据集上,利用自定义的MLP、CNN 和ResNet20 网络进行训练,并通过不同隐私预算下的多组实验和对比。实验结果表明,本文算法在满足差分隐私的条件下具有较好的可用性。由于本文提出的带扰动参数优化方案只在横向联邦协作和客户-服务器架构下进行验证,下一步将在纵向联邦学习和对等架构下验证方案的有效性。另外,将继续研究使用数据非独立同分布时模型准确率的优化问题。
