SM9 中高次幂运算的快速实现方法

王江涛，樊 荣，黄 哲

（中国船舶集团有限公司第七二二研究所，武汉 430205）

0 概述

近年来，基于椭圆曲线上配对的密码体制引起了人们的极大兴趣，由于双线性对独特的性质，可以构造许多其他加密算法无法完成的加密协议，因此出现了大量基于双线性对的研究成果，其中有许多新的的协议，包括一轮三方密钥交换［1］、基于身份的加密［2］、基于身份的签名［3］、短签名方案［4］等。

我国国家密码管理局于2016 年正式发布基配对的SM9 标识密码算法［5］，于2018 年被纳入国际标准，该算法以用户的身份信息作为公钥，简化了可信第三方认证中心（Certificate Authority，CA）的秘钥管理环节，从而解决了由高频认证引发的信息堵塞问题，非常适合海量用户之间的安全通信，在云计算、物联网等海量用户的新兴领域中［6］，SM9 密码算法具有明显的优势。

基于配对的密码协议只有在高安全级别上以高效计算双线性配对的情况下才能实现。得益于MILLER 等［7］提出的在椭圆曲线上以除子的标量乘来计算有理函数的迭代算法，实现以线性复杂度的开销去计算双线性对，并用于计算weil 对（对称双线性对）的目的。文献［8］给出计算更简便的Tate 对（非对称双线性对）。文献［9-11］在Tate 对的基础上通过构造特殊结构的双线性Eta 对、Ate 对和Atei 对来优化双线性对的计算量。文献［12］定义了R-ate对，通过两个特定线性对的比值，减少Miller 算法中的循环次数。文献［13-15］优化了BN 曲线上R-ate对的计算，主要针对其中的Miller 循环和最终幂运算，对Miller 循环中的同构映射进行分析，将循环中的点加，倍点和线性函数的运算从十二次扩域降低为二次扩域.文献［16-17］将最终幂运算进行幂次分解，用基域的组合多项式来表示运算困难的大幂次项，并利用有限域和扩域上Frobenius 映射进行加速，文献［18］使用Comb 固定基［19］对SM9 中签名部分的高次幂进行优化。

密码算法的底层运算有大量大数计算，文献［20］提出蒙哥马利算法，将大数的模乘改为3 个大数乘法，这也使得对称加密的底层运算可以实现，文献［21］针对R-ate 对提出混合模乘（Hybrid Modular Multiplication，HMM），其核心思想是将基域的数表示为特征数的多项式形式，引入了多项式情况下的蒙哥马利算法，将对于大数的模乘转化到特征数上的模乘，但由于SM9 中特征数的权重比文献中使用的权重大，所以使用该算法并不合适作为SM9 的底层运算。文献［22］提出基于字的蒙哥马利乘（MWR2MM），将乘数均转化为短整数乘法，更有利于硬件实现。文献［23］提出迭代字蒙哥马利乘（IDDMM），将模也转化为短整数，在基于MWR2MM基础上增加了基础乘法的位宽。文献［24］提出基于蒙哥马利的求逆运算，使蒙哥马利域的大数在求逆后，不用再进行两次转入域操作。

本文利用十二次扩域的分圆子群的性质，使用快速平方算法，该算法相较于传统平方算法需要的基域乘法数量降低了1/2。该平方算法应用在SM9的高次幂运算上，包括R-ate 最终幂和签名算法中，最终幂中的高次幂采用反复平方-乘法算法和NAF算法，签名算法中高次幂采用Comb 固定基算法。底层的大数模乘采用文献［20］中的蒙哥马利运算，相较于IDDMM，更有利于本文架构实现，硬件使用Xilinx Artix-7 系列的XC7A50T，架构选用基于专用指令集处理器（Application Specific Instru-ction Set Processor，ASIP）的微码编程，在控制硬件资源开销的同时降低时钟周期，从而提高性能。

1 基础算法

1.1 BN 曲线上的R-ate 对

文献［25］提出一种在素域Fp上构造配对友好的常曲线的方式，BN 曲线定义了椭圆曲线［26-28］方程χ(Fq)：y2=x3+b，对应嵌入度k为12，素域的特征p、群的阶r、Frobenius 迹tr由参数t定义为式（1）所示：

其中：t∊Z 是一个任意的整数，使得p及r均为素数。

SM9 使用了定义在BN 曲线上的R-ate 对，双线性对中定义了3 个阶为N的循环群，分别是加群G1、G2和乘群GT，G1的生成原是P1，G2的生成原是P2，G1表示χ(Fp)[r]∩Ker(πp-[1])，G2表示χ(Fp)[r]∩ Ker(πp-[p])，χ(Fq)[r]为椭圆曲线上的r扭转点，核Ker(πp-[p])为{P|πp(P)-[p]P=O}，O 定义为椭圆曲线中的无穷远点，在群G1、G2、GT中存在映射G2×G1→GT满足双线性、可计算性和非退化性，对应映射关系如式（2）所示：

其中：Q∊G2,P∊G1；fr,Q为Miller函数；πp表示Frobenius 映射πp(x,y)=(xp,yp)；lR,Q(P)为椭圆曲线上过R,Q的直线方程在P点处的值。R-ate 双线性对的计算可由算法1 实现。

算法1BN 曲线上的R-ate 对

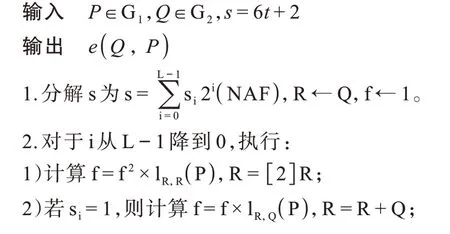
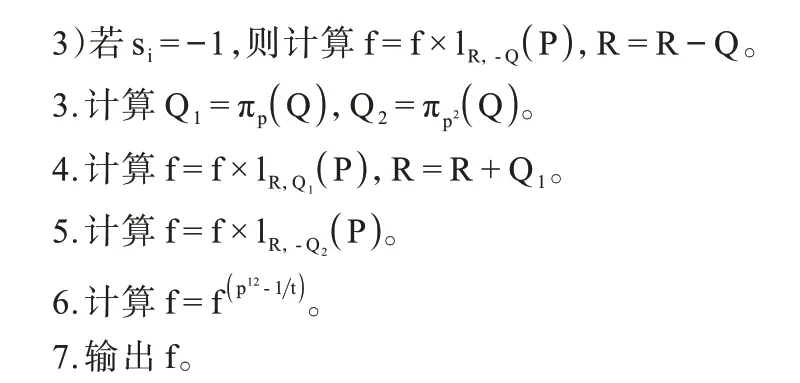
算法1 中的计算可以分解为图1 中基域的加减乘和求逆运算，其中较为复杂的运算为第2 步Miller循环和第6 步的最终幂运算，最终可以转化为基域的加减乘和求逆运算。

图1 R-ate 算法的实现Fig.1 Implementation of R-ate algorithm

1.2 NAF 算法

采用NAF 算法对标量k进行编码，是指将使用1，0 表示二进制序列k=(sm-1,…，si,…，s1,s0)bin，其中si∊{0,1}，变换为用1、0 和-1 表示的形式。即标量k的NAF 编码为k=(km,…，ki,…，k1,k0)NAF，其中ki∊{-1,0,1}，且首位km≠0，具体表示如式（3）所示：

标量k的NAF 编码算法描述如算法2 所示。

算法2标量k的NAF 编码算法

令lNAF(k)表示标量k采用NAF 编码方法的编码长度，则有，下面给出实用的NAF 编码性质：

1）长度最多比二进制形式编码的长度多1；

2）非零元素平均个数为m 3；

3）非零元素-1，1 不会相邻。

在反复平方-乘法运算中，可以使用性质2）减少乘法数量。

1.3 Comb 固定基

SM9 签名运算中高次幂可以预存点，通过查找表运算高次幂gr，将幂指数通过基于Comb 固定基的方式进行查表计算。指数r可以表示成式（4）中两种形式，其中

当指数运算时，所有Ri位置相同的比特可以同时处理，将需要预先存储的元素表示为，其中m按位展开为[m7,m6,m5,m4,m3,m2,m1,m0]∊[0,255]，所以共需要预存256 个十二次扩域元素，算法实现先按照图2 对r进行比特重组，将以Ri表示变为以ai表示，再使用算法3 进行计算。

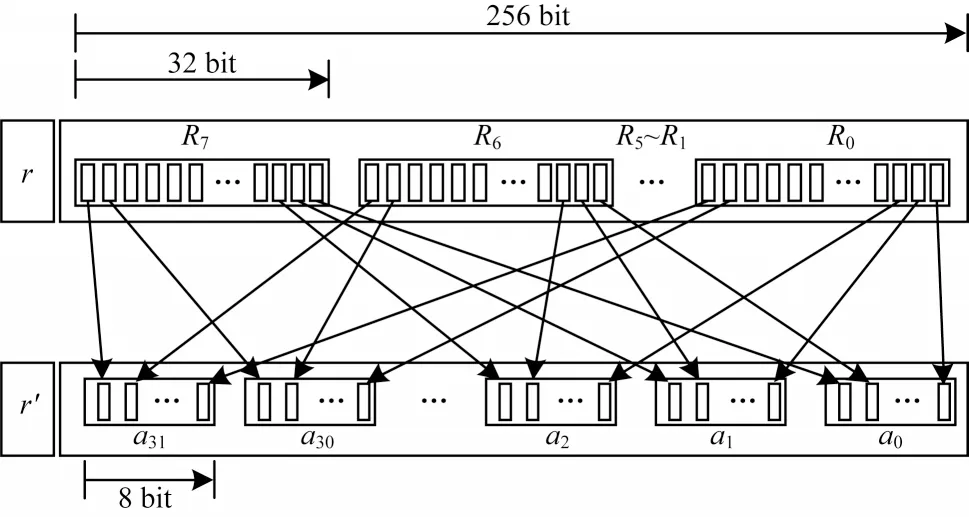
图2 幂指数r 的比特重组Fig.2 Bit recombination of power exponent r

算法3基于Comb 基的高次幂运算

使用Comb 算法优化前，如果预存每个比特位上的平方值，也需要预存256 个十二次扩域元素，运算开销为128 次GT域上的乘法。优化后，在使用相同存储开销的情况下，运算开销减少为GT域上31 次乘法运算和31 次平方运算。

1.4 SM9 签名算法

密钥生成中心（Key Generate Center，KGC）产生随机数ks∊[1,N-1]，计 算G2元素Ppub-s=[ks]P2并作为签名主公钥，计算G1元素dSA=[t2]P1作为签名密钥，t2通过哈希计算用户标识ID 得到。

令待签名的信息为M，KGC 生成(Ppub-s,dSA)密钥对，签名后得到数字签名为(h,s)，签名流程为：

1）计算GT中的元素g=e(P1，Ppub-s)；

2）产生随机数r∊[1,N-1]；

3）计算群GT中的元素w=gr；

4）计算整数h=H2(M||w,N)；

5）计算整数l=(r-h)modN；

6）计算群G1中的元素S=[l]dsA；

7）消息的签名值为(h,S)。

在签名算法中，当KGC 下发了Ppub-s后，由于P1也是固定变量，因此签名中g可以提前预计算并存储起来，不用每次签名都要重新计算，所以签名的效率往往是验签效率的数倍。

2 基于分圆子群的快速平方算法

2.1 扩域平方算法

SM9 中选取的是式（5）的1-2-4-12 塔式扩张［29］，对应的不可约多项式分别为x2-α(α=-2)，x2-u(u=，其计算式如下：

在扩域Fq4中将a表示为a1+a0v，其中a1、a0均表示二次扩域元素。使用算法4 计算4 次扩域元素的平方，相较于直接用Karatsuba 算法计算，平方算法需要将基域的乘法从9 次降低为6 次。

算法4上的平方运算

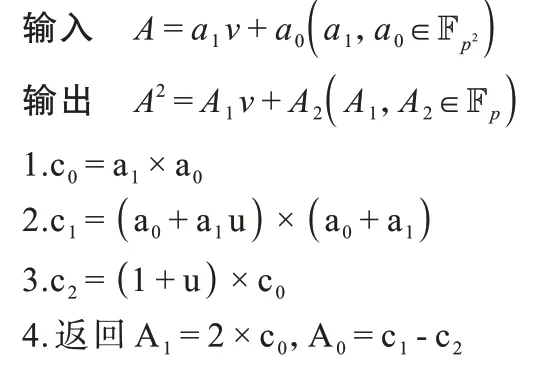
在扩域Fq12中α表示为a+bw+cw2，其中a、b、c为扩域Fq4元素，应用塔式扩张的乘法运算规则将平方项α2表示为式（6）：

u、v、w分别为二次、四次和十二次扩域元素，关系为-2=u2=v4=w12，采用算法5 使运算开销从3 个四次扩域的平方和乘法降低为3 个平方和2 个乘法，即需要36 个基域乘法。

算法5上的平方运算

2.2 快速平方算法

算法1 中R-ate 对的计算包括Miller 循环和最终幂运算，由式（7）中分圆多项式的定义可知，在最终幂中部分表示为其中：Φ4(p)=p2+1；Φ12(p)=p4-p2+1。由费马小定理可知，Fp12的元素f对应有fp12-1=1，根据式（8）给出的分 圆子群 的定义，令α=f(p6-1) (p2+1)，可 得到α∊GΦ12(p)。

根据Frobenius 映射原则，将α在GΦ12(p)群中满足的性质αp4+1=αp2展开，可得到式（9）：

其中：fr表示Frobenius 常数，值为；aˉ表示扩域元素a的共轭。将式（9）展开并约减w3-v和Φ12(fr)=，得到式（10）：

式（10）中提供了式（6）中乘项ab、bc、ac另一种等效求解方式，如式（11）所示：

算法6 为GΦ12(p)上的平方运算。

算法6GΦ12(p)上的平方运算

将十二次扩域群上的平方算法5 和十二次分圆子群的平方算法6 进行对比，由于共轭运算不会增加额外的加减法，因此前者需要36 个基域乘法和40 个基域加减法，后者需要18 个基域乘法和36 个基域加减法。底层运算的效率主要受制于基于蒙哥马利算法的大数模乘运算，使用快速平方算法可以减少接近50%的模乘运算。本文使属于分圆子群的十二次扩域元素采用快速平方算法，该算法使用的底层大数运算也是基于蒙哥马利的模乘和大数加减运算，并不会造成额外的资源开销。

2.3 基域乘法数量分析

在R-ate 对中高次幂ft的运算中，幂指数t为SM9 中的参数t，对应值为0x600000000058F98A，汉明重量为13，数据位宽为63。由于底数f是变化的，因此采用反复平方-乘法算法，共需要12 个十二次扩域乘法和63 个平方运算，对指数t使用NAF 后可以将其汉明重量降低为11，数据位宽变为64（NAF 会增加1 位数据位宽），在十二次分圆子群中f(-1)可以转化为共轭fˉ计算，因此优化后，仅需要10 个扩域乘法及64 个在第2 节引入的在分圆子群上的快速平方。

在签名中高次幂gr运算中，幂指数r为256 bit位宽的随机数，由于底数g是固定的，因此可以预存一些计算值，采用基于Comb 固定基计算，预存256 个十二次扩域的点，根据查找表计算结果需要31 个扩域平方和31 个扩域乘法。相比采用反复平方-乘法算法，对应计算结果需要256 个扩域平方和128 个扩域乘法，即采用NAF（经过R-ate 对计算后，仍保留分圆子群的性质，即模逆计算可以转化为共轭计算）降低也需要约80 个扩域乘法，如果无法使用查找表的场合，可用后者进行优化。表1 所示为采用快速平方算法前后的乘法数量对比。

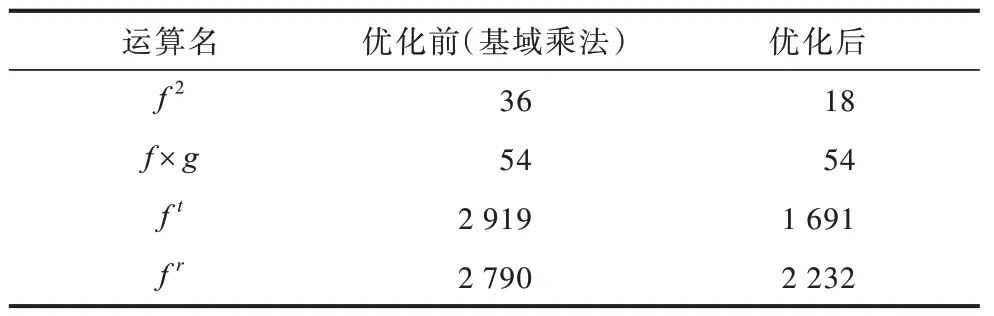
表1 高次幂基域乘法数量对比 Table 1 Comparison of multiplication of higher power base fields

3 ASIP 结构设计

由于SM9 逻辑较为复杂，将其拆分成基域的运算需要复杂的控制信号，因此硬件架构采用ASIP，其核心思想是针对某一特定目标的应用领域定制一套专用指令集，然后开发出与该指令集相对的体系结构，最终根据该体系结构高效地构造复杂算法的专用微处理器结构，它具备通用处理器（General Purpose Processor，GPP）的可编程性和专用集成电路（Application Specific Integrated Circuit，ASIC）的 高速处理特性。

从硬件角度来看，FPGA 具有片内资源丰富、可重新配置、可实现大规模电路等特点，而且基于重用电路性质可以缩小设计周期和提高资源利用率，因此FPGA 可以用作ASIP 的载体，在基础电路固定的情况下，ASIP 可以通过编程的方式实现相应的复杂算法，同时也具备了可扩展移植的特点。在ASIP 的设计中，选择合适的体系架构是关键性问题，目前较为主流的体系架构为精简指令集计算机（Reduced Instruction Set Computer，RISC）结构和复杂指令集计算机（Complex Instruction Set Computer，CSIC）结构，相比于CSIC，RISC 采用固定长度的编码长度，简化了指令系统，减少了指令译码的线路规模。

本文采用自定义的32 bit RISC 指令，指令格式如表2 所示，表中第1 行数据代表比特位，指令集的设计遵循精简、高效、可重用的原则，如普通加减法和模加减法在选用不同模式时使用相同的电路结构，在所有格式中，指令集架构（Instruction Set Architecture，ISA）将源寄存器（RegS）、目的寄存器（RegD）、源控制和状态寄存器（Control and Status Register，CSR）、CsrS 以及目的CSR（CsrD）固定在同样位置，若使用立即数能保证编码位置的严格对齐，从而降低译码模块的复杂度。

表2 指令格式 Table 2 Instruction format

基础通用指令主要用作控制程序指针，包括Nop指令、Call指令、Return指令、Goto指令，后 面3 条指令可实现较为复杂的逻辑控制，Type-I 类型指令主要用于实现对RegFile 寄存器的读写操作，包含RegCsrEachSet 指令实现CSR 与寄存器的双向同时赋值或基于寄存器赋值的延伸使用方式，RegSetWith 指令以及GetPointToReg 指令实现寄存器间数据的赋值操作以及RegInc 指令实现寄存器中数据的自加一运算。Type-II 类型指令包括指令CSRSetWithImm，用于将相应的CSR 赋值为基数的值。Type-III 主要包含指令BcRegERqImm，该指令实现有条件跳转，也是构建循环的必须指令。

本文设计的ASIP 整体结构框如图3 所示。

图3 ASIP 的整体结构Fig.3 Overall structure of ASIP

硬件层实现了有限域算数单元扩充的通用处理器，因此确保了平台的灵活性和通用性，对应模块的功能如下：

1）算法核单元Core 通过程序定序器（Program Sequence）处理程序存储器（Program Rom）中的二进制指令，相应指令解析流程为指令获取IF、指令解码DE 以及指令执行EXE，解析后执行相应的控制和数据传递功能，并提供下一条指令在程序存储器中的地址。

2）算数运算单元ALU 中包括基于蒙哥马利和Karatsuba 算法完成基域的乘法和求逆，由于大量的基域加减法和乘法在执行时间上重合，因此加减法单元被设计在Core 中，从而可以进行并行处理以减少总时钟周期。

3）组件单元中包括取预存值的模块Ng、降低汉明重量的NAF 模块以及计算高次幂的Comb 基模块等，ALU 和组件均由控制模块给出执行信号，并占用相同的数据总线。

4）通用寄存器组（General Purpose Register Set，GPRS）为ALU 提供操作数、暂存运算结果以及初始化时预存常参量的功能。

5）控制和状态寄存器Csr 用于促进Core 和ALU之间的数据传递。

逻辑层汇编编译器将基于RISC 指令集编写的汇编文件编译成典型FPGA ROM 宏单元的程序内容配置文件，汇编文件的编写需考虑到乘法和其他操作的并行性，编译器由Python 编写，具有完整的错误检查功能，利于软件程序的自检。

4 实验结果与分析

为验证快速平方算法并对其资源开销和运算性能进行评估，本文使用SpinalHDL 语言实现，基于Xlinx Artix-7 FPGA（XC7A50T-1FTG256C）进行实际测试，并分析硬件实现性能和资源开销。

4.1 硬件资源分析

为评估硬件资源所需的开销，本文将实现SM9算法的ASIP 以167 MHz 的时钟频率进行综合。本文底层通用运算模块的硬件实现上重点在于充分利用ASIP 的可编程性，最占用资源的模块为蒙哥马利模乘Mul 和模逆Inv 模块。模乘器的实现并未采用状态机，而是采用全流水的形式，在扩域乘法上，连续乘法结果的输出可以极大降低时钟周期。模逆器可以选择用微码实现，从而省去接近13.6%的硬件资源开销，本文考虑到该密码算法核的通用性，选择保留模逆器。算法核单元Core 为最需要减低面积的模块，主要方向为重利用寄存器，最终为放置多组算法核提供了可行性，本文算法的各个模块硬件综合资源开销数据如表3 所示。分别使用查找 表（Look-Up-Table）、块随机 存储器（Block Random Access Memory，BRAM）、数字信号处理器（Digital Signal Process，DSP）作为硬件综合资源开销的单位。由表3 可知，本文算法总体资源占用相比于文献［18］算法，需要的硬件资源LUTS 有所减少。

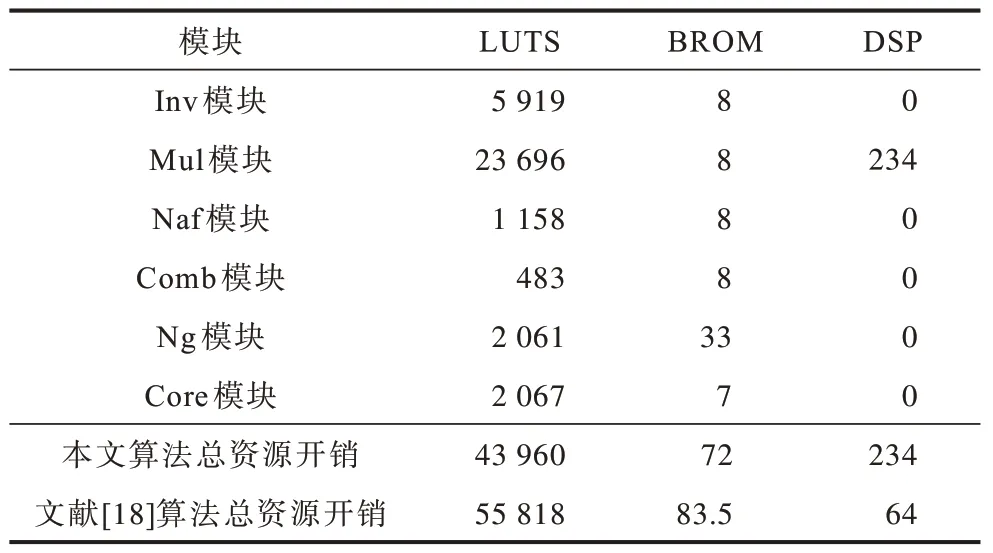
表3 本文算法各模块硬件资源开销 Table 3 Hardware resource cost of each module of algorithm in this paper

4.2 时钟周期分析

表4 给出了各基本运算的时钟周期数，本文为了降低时钟周期，令底层蒙哥马利模乘采用全流水的形式，即两个连续的乘法运算可以无延时地输入乘法器，从而可以更好地利用ASIP 的可编程性。大数的模加减运算在算法核Core 中，由于ASIP 的数据交互在Core 和Csr 之间进行，需要将加数分别从Csr送入Core 再取出结果，至少需要3 个及以上时钟周期。本文采用流水加法，可以连续送入加数，在取模的同时送入下一组加数，从而减少到两个周期。汇编的灵活性使得流水加减法和44 级乘法流水可以交替进行，经优化运算周期数表3 为最终优化结果，其中f×g，f2分别为对应扩域的乘法，相比于基本十二次扩域元素的平方，分圆子群上的平方运算时钟周期数降低了约47.14%。ft，gr为R-ate 对和签名算法中的高次幂运算，kP为签名中的点乘运算。

表4 不同基本运算的时钟周期数对比 Table 4 Comparison of clock cycles of different basic operations 单位：个

SM9 签名运算中包含高次幂和G1点乘两个相对复杂的运算，表5 所示为不同平台签名时间的对比，文献［30］算法基于Arria10 软件平台实现，但并未使用Comb 固定基，性能相对较差，文献［18］算法基于XC7K325T 硬件平台，为了节省高次幂所占用的存储空间，只预存4 个扩域值，并令扩域平方和乘法使用相同的结构，签名时间较长。文献［31］算法基于i5-4590 CPU，预存的数值与本文一致，但未使用快速平方算法和ASIP 硬件架构，因此性能较本文也差一些。综上分析，采用ASIP 的硬件架构，在签名算法中使用快速平方算法对性能有较大提升。

5 结束语

本文根据R-ate 对映射出来的扩域元素属于十二次分圆子群的性质，推导出基于该子群的快速平方算法，并将该平方算法应用在SM9 签名和验签中，签名中高次幂减少了20%的基域乘法数量，验签中高次幂减少了42.1%的乘法数量。本文针对SM9的特性完成了基于ASIP 的硬件设计，并在Xilinx Artix-7 FPGA 平台上进行了实际测试。实验结果表明，在167 MHz 的时钟频率条件下，不增加额外的硬件资源开销，完成一次SM9 签名的时间仅为0.244 ms。下一步将尝试利用IDDMM 算法，优化底层大数算法，在相同性能的情况下减少硬件资源开销。