基于多尺度特征融合与双注意力机制的多元时间序列预测

韩 璐，霍纬纲，张永会，刘 涛

（1.中国民航大学 计算机科学与技术学院，天津 300300；2.潍坊学院 计算机工程学院，山东 潍坊 261061）

0 概述

多元时间序列（Multivariate Time Series，MTS）是指在一段时间内依照固定的采样率对某种过程进行观测并记录一组包含多个变量的数据［1］，本质上是反映这些变量随着时间不断变化的趋势。对MTS的历史观测值进行分析，并估计未来某个时刻值的过程称为时间序列预测。多元时间序列预测在商业、医学、气象等领域具有重要的研究价值。

时间序列预测方法可大致分为统计方法、传统机器学习方法和深度学习方法。统计方法主要采用统计学知识对时间序列中蕴含的发展过程、方向和趋势进行建模并预测，常见的模型有自回归（Auto-Regressive，AR）模型、移动平均（Moving Average，MA）模型等。然而，此类方法具有较低的表达能力，不能处理复杂数据中的非线性关系，因此，预测准确率比较有限。传统机器学习方法包括支持向量机［2］、贝叶斯网络［3］、高斯过程［4］等，克服了统计方法的弊端，在时间序列预测方面展现出较优的效果。但是传统机器学习方法往往需要复杂的特征工程且特征适应性差，导致预测精度呈现一定的不稳定性［5］。

深度学习因其强大的表征和拟合能力而受到研究人员的关注，已经被广泛应用于时间序列分析的相关领域［6-8］。深度学习方法主要有循环神经网络［9］（Recurrent Neural Network，RNN）及其变体长短时记忆［10］（Long Short-Term Memory，LSTM）网络和卷积神经网 络（Convolutional Neural Network，CNN）［11-12］2 类模型结构。将循环神经网络及其变体长短时记忆网络作为单元组件，对时序数据进行预测。文献［13］通过结合RNN 和概率模型提出一种混合预测方法，在提取全局非线性特征的同时估计局部随机性变化趋势，提高预测精度。以卷积神经网络作为特征提取器，通过构建深层卷积模型以获得强大的特征提取及预测能力。与循环神经网络模型结构相比，基于CNN 的时间序列预测模型具有计算效率高、训练难度低等特点，在多元时间序列预测方面具有一定优势。文献［14］提出DeepGLO 模型，利用时序卷积解决极高维时间序列的预测问题。

上述工作都只针对深度学习的直接应用，而没有结合MTS 数据及其特征的特点。在时间序列中各变量的变化往往具有不同的时间跨度，存在多种尺度特征。对于MTS 预测任务，充分利用多尺度特征能够增强网络的预测能力。文献［15］提出的LSTNet 通过结合CNN 和RNN 捕获MTS 中的短期和长期尺度特征，大幅提高预测准确率。针对负荷数据中的周期性波动特征，文献［16］基于LSTM 结构构建一种Seq2seq 模型，实现数据相关性建模并对其进行预测。在计算机视觉领域，文献［17］所提GoogleNet 的核心是通过Inception 结构处理图像中不同尺度的语义信息。基于此，MTGNN 模型［18］将Inception 结构引入到MTS 预测中，利用多个不同大小卷积核和膨胀卷积［19］提取多尺度特征，在预测方面表现更优的性能。CNN 卷积核是一种特征检测器，各卷积核捕获数据中不同方面的特征［20］，这些特征对预测的重要程度不尽相同。为此，研究人员需要利用注意力机制以聚焦对预测有重要贡献的关键时序特征，抑制其他无用特征。文献［21］提出TPALSTM 模型，利用时序模式注意力机制关注与待预测值更相关的时序区间。文献［22］提出DAFDCRNN 模型，利用注意力机制对时间序列的特征相关性进行建模，通过学习其中的长期时间依赖来提升预测精度。文献［23］提出的AttAR 模型引入时不变注意力机制，进一步区分性地利用时序特征。

上述研究表明多尺度特征及注意力机制在MTS预测方面具有较优效果，但是依然存在不足之处。时间序列在不同时间跨度下呈现完全不同的走势，其对应的尺度特征也对预测发挥不同程度的作用。现有方法不能自适应提取、选择并融合这些尺度特征，限制了模型的预测性能。上述注意力机制只从时间维度聚焦相关影响因素，而没有对特征的长时序、多通道方面重要程度加以区分。

本文提出一种基于多尺度时序特征融合与双注意力机制的多元时间序列预测网络FFANet。利用多尺度时序特征融合模块从时间序列中提取多尺度特征，并自适应选择和融合多尺度时序特征。双注意力模块（Dual-Attention Module，DAM）分别对每个变量特征从时序和通道2 个维度计算特征重要程度并分配权重，使FFANet有区分地利用多尺度特征。

1 问题定义及符号表示

本文将 MTS 的观测样本表示为X=(X1,X2,…,XT) ∊RN×T，其中，T为该MTS 观测样本的时间步总数，N为变量数目。将单个时间步上的MTS 样本表 示为Xt=(xt,1，xt,2，…,xt,N) ∊RN，xt,n表示第n个变量在第t个时间步上的观测值，其中，1 ≤t≤T，1 ≤n≤N。本文的目标是基于历史d个时间步的观测值χt=(Xt-d,Xt-d+1,…,Xt) ∊RN×d，预测未来第h个时间步的值Xt+h∊RN，其中，d是在指定的训练预测模型时MTS 样本时间步长。

MTS 预测是滚动预测过程。在t时刻，基于历史观测值χt=(Xt-d,Xt-d+1,…,Xt)预测未来第h个时间步的值Xt+h。类似地，在t+1 时刻，基于历史观测值χt+1=(Xt-d+1,Xt-d+2,…,Xt+1)预测值Xt+h+1。

2 FFANet 模型

2.1 整体架构

本文设计FFANet 模型的整体架构如图1 所示，该模型由多尺度时序特征融合模块FFM、双注意力模块、压缩层和输出模块构成。FFANet模型中多次使用FFM、DAM、图卷积模块和压缩层的结构，下文中将该结构称为“Section”结构。

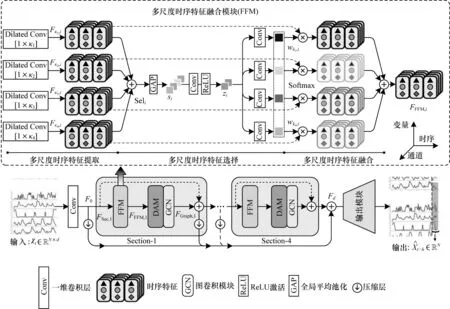
图1 FFANet 的整体结构Fig.1 Overall structure of the FFANet

给定MTS 样本χt∊RN×d，FFANet 模型首先利用一维卷积层将其映射为3 维特征F0∊RN×d′×C，d′为时序特征长度，C为特征通道数。F0的计算如式（1）所示：

其中：HSF(∙)为卷积操作。FFANet 模型的 主干部 分由4 个Section 结构组成，用于挖掘特征F0的深层多尺度特征。为了避免梯度消失，在每个Section 内设计Section 结构的输入与图卷积模块输出相加的残差连接，同时，将对每个Section 的输出进行压缩时序长度后，通过跳跃连接求和得到Fd∊RN×1×C，即输出模块的输入特征为Fd。最后，通过卷积操作将输出模块特征Fd映射为最终预测值

FFANet 模型通过训练最小化真实值Xt+h与预测值之间的l1损失以更新网络参数，具体损失函数如式（2）所示：

其中：f(∙)表示FFANet 模型函数；Θ表示其中的网络参数。

2.2 多尺度时序特征融合模块

为了有效利用MTS 中的多尺度时序特征，本文提出多尺度时序特征融合模块，包含多尺度时序特征提取、多尺度时序特征选择和多尺度时序特征融合3 个阶段。

在多尺度时序特征提取阶段，本文引入时序卷积层［18］，使用J组尺寸为1×κj(1 ≤j≤J)的一维膨胀卷积提取Section 结构的输入特征，以获取不同尺度的时序特征。给定第i(1 ≤i≤I)层Section 结构的输入FSec,i∊RN×d′×C，每组特征提取过程如下：

其中：q表示膨胀因子；pi表示该层卷积膨胀率；ht,n∊RC表示输入特征FSec,i中第n个变量在t时刻的隐状态；fκj,i∊Rκ×C表示尺寸为1×κj的膨胀卷积核；Fκj,i(n,t,pi)表示由尺寸为1×κj的膨胀卷积（膨胀率为pi）对 第n个变量提取t时刻的 隐状态；δ表示Re LU 激活函数。

在多尺度时序特征选择阶段，FFANet 模型自适应调节上述多尺度时序特征权重，以实现特征选择。首先，多尺度时序特征选择阶段接收来自提取阶段4 个并行的不同尺度时序特征，对该特征进行元素求和，生成包含全局信息的特征Seli∊RN×d′×C，计算式如下：

随后，在变量和时序维度上利用全局平均池化层（Global Average Pooling，GAP）对特征Seli生成特征si∊RC，对于sc,i⊂si，计算式如下：其中：fGAP(∙)表示全 局平均 池化操 作。FFANet模型进而利用卷积操作提取特征si的全局特征zi∊RC/r，r表示通道压缩率。最后，特征zi通过J组并行的卷积层（每个尺度特征对应一层卷积层）生成J个特征描述符zj,i∊R1(1 ≤j≤J)。

最后，根据式（6）将上述4 个特征描述符生成不同尺度特征对应权重：

其中：wκj,i为第i(i≥1)层Section 结构由尺寸为1×κj的膨胀卷积所提取特征的权重。

在多尺度时序特征融合阶段，FFANet 模型将上述权重分别通过相乘作用于对应尺度特征并求和，实现多尺度时序特征融合，具体计算如下：

2.3 双注意力模块

本文设计了双注意力模块，该模块的结构如图2所示。双注意力模块由时序注意力机制TA 和通道注意力机制CA 组成。

图2 双注意力模块结构Fig.2 Structure of the dual-attention module

在双注意力模块中，首先将第2.2 节多尺度时序特征融合模块输出的特征FFFM,i∊RN×d′×C作为输入，由卷积层、ReLU 激活函数和卷积层构成的卷积组提取特征，计算式如下：

其中：Groupatt,i(∙)表示第i层Section 结构中 双注意 力模块首端的卷积组；W(att-1),i和W(att-2),i分别表示该卷积组中的2 层1×3 卷积核的权重；Fatt,i∊RN×d′×C表示该卷积组的输出。

2.3.1 时序注意力机制

为了从MTS 中区分与待预测点更相关的时序，进而对其进行聚焦，本文设计时序注意力机制。

首先，在通道维度上利用平均池化层和最大池化层对输入特征Fatt,i进行降维，分别生成特征F（avg-t）,i∊RN×d′×1和F（max-t）,i∊RN×d′×1；然 后，将两者 拼接后通过卷积将双通道特征压缩为单通道；最后，使用Sigmoid 激活函数对时序权重进行归一化，生成时序注意力权重Ti∊RN×d′；最终，将时序注意力权重与输入特征对应元素相乘，生成不同权重的时序特征。时序注意力机制的运算过程如式（9）所示：

其中：σ表示Sigmoid 激活函 数；Htemp,i(∙)表示卷积操作；[F(avg-t),i,F(max-t),i]表示池化并拼接后的特征；AvgPoolC(∙)和MaxPoolC(∙)分别表示通道维度的平均池化和最大池化层；Ti表示时序注意力权重。

2.3.2 通道注意力机制

本文引入的通道注意力机制［24］如图2 所示。首先，CA 采用与TA 同样的方式，通过全局平均池化和全局最大池化层对特征Fatt,i各通道的全局时序和变量特征进行压缩，生成2 组特征F(avg-c),i,F(max-c),i∊RC；然后，将上述2 组特征的对应元素求和后通过卷积组建模通道之间的相互依赖性，自适应地判别各通道的重要程度；最后，由Sigmoid 激活函数生成通道注意力权重Ci∊RC，并通过逐元素相乘将权重应用于特征Fatt,i中。通道注意力机制的运算过程如式（10）所示：

其中：Groupchannel,i表示由卷积层、ReLU 激活函数和卷积层 构成的 卷积组；AvgPoolNT(∙)和MaxPoolNT(∙)分别表示时序和变量维度的平均池化和最大池化层；Ci表示通道注意力权重。

时序注意力权重和通道注意力权重通过相乘应用于特征Fatt,i后生成双注意力模块的输出FDAM,i∊RN×d′×C：

2.4 图卷积模块

在MTS 变量对之间通常具有潜在的依赖关系。为此，本文引入图卷积模块［18］，包含图学习层和图卷积层，自适应捕获变量对之间的关联关系。

图学习层的目标是学习变量间的动态空间依赖关系，并用邻接矩阵表达。首先，将随机初始化的嵌入矩阵E1,E2∊RN×e表示特 征M1,M2∊RN×e，N和e分别表示图节点（变量）数量及图节点嵌入维度。M1、M2、邻接矩阵A∊RN×N计算过程为：

其中：q1和q2表示全连接网络参数。

图卷积层计算过程如下：

其中：G为图卷积层数；Fg,i为第g层图卷积输出；α为图卷积层的超参数表示归一化的邻接矩阵，为A矩阵的度矩阵，表示单位矩阵。最后，根据式（14）对图卷积层结果F1,i,F2，i,…,FG,i进行计 算：

其中：FGraph,i∊RN×d′×C表示图卷积模块的输出特征。

2.5 压缩层与输出模块

在FFANet 模型中，特征F0和各Section 结构的输出特征都经过压缩层以缩短特征长度，其本质是利用与给定输入等长的卷积核逐变量卷积。给定的时序特征Fdown,i∊RN×d′×C为：

特征Fd∊RN×1×C通过跳跃连接对各压缩特征求和获得，计算过程如下：

其中：Hdown,i代表特征Fdown,i所对应的压缩层函数。

输出模块由卷积层、Re LU 激活函数和卷积层构成，根据式（17）将特征Fd映射为最终预测值：

其中：Wout-1和Wout-2分别表示2 层卷积核的权重。

3 实验结果与分析

3.1 实验设置

3.1.1 数据集

为验证本文模型的性能，本文实验选取UCI 机器学习库中4 种不同领域的公开数据集。该数据集的相关统计信息如表1 所示。

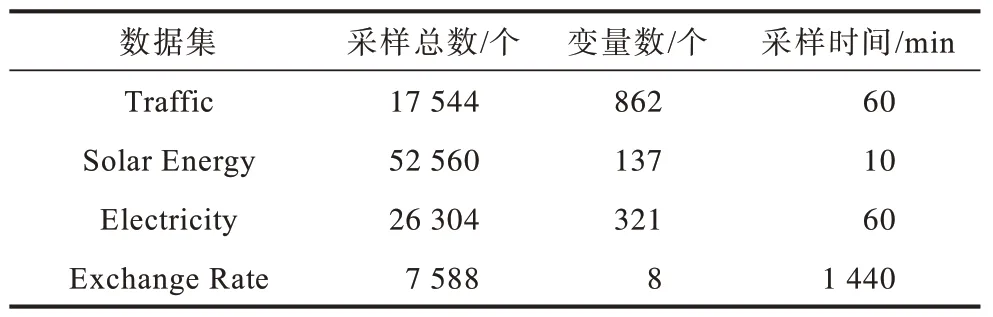
表1 时间序列数据集详细信息 Table 1 Details information of time-series datasets

Traffic 为交通数据集，统计了在美国旧金山湾区高速公路48 个月（2015 年1 月1 日—2016 年12 月31 日）内通过862 个传感器测量得到的道路占用率。Solar Energy 为太阳能数据集，统计了2006 年阿拉巴马州137 个光伏发电厂的太阳能发电记录。Electricity 为电力数据集，统计2012—2014 年葡萄牙321 个用户每小时的电力消耗量。Exchange Rate 为汇率数据集，统计了从1990—2016 年内包含澳大利亚、英国、加拿大、瑞士、中国、日本、新西兰和新加坡8 个国家的每日汇率。本文实验的所有数据集被划分为训练集（60%）、验证集（20%）、测试集（20%）。从4 个数据集抽样的部分变量如图3 所示。

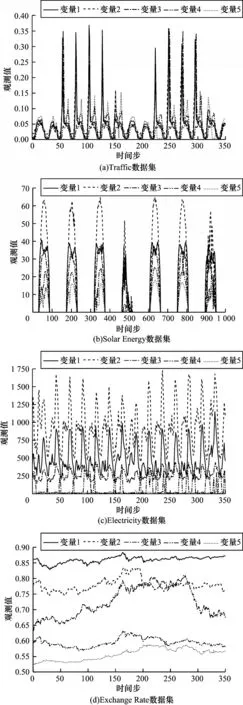
图3 不同数据集的可视化结果Fig.3 Visualization results among different datasets

3.1.2 实验细节

数据指标：本文实验采用相对平方根误差（Root Relative Squared Error，RRSE）和经验 相关性系数（Empirical Correlation Coefficient，CORR）作为评价指标。RRSE 是评价预测结果与真实值的偏离程度，CORR 是评价模型滚动预测步序列取值与真实值的相关程度。RRSE 越低表示预测效果越好，CORR 越高表示预测效果越好。

实验环境：FFANet 模型代码全部由Python3.6 实现，使用PyTorch 深度学习框架搭建，并在NVIDIA GeForce RTX 3080 Ti GPU 上进行训练。

参数设置：FFANet 模型的相关超参数取值如表2 所示。模型使用Adam 优化器，学习率为0.001，梯度衰减率为0.000 1，epoch 为100。

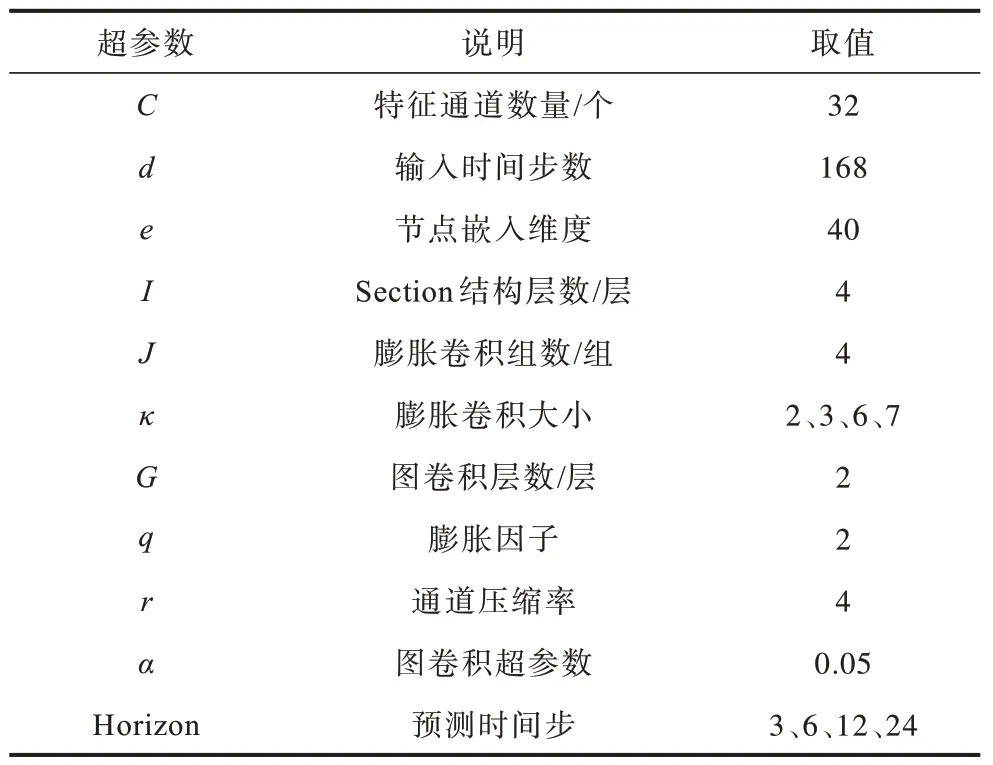
表2 超参数设置Table 2 Hyperparameter settings

3.2 结果分析

3.2.1 对比实验

为评估本文模型的预测效果，本文选择以下7 种主流的MTS 预测模 型：1）AR 是一种自回归模型；2）VARMLP［25］是一种基于自回归方法和全连接网络的混合模型；3）RNN-GRU 是一种使用GRU 隐藏层的循环神经网络；4）LSTNet-skip［15］是一种结合卷积神经网络和递归神经网络的深度预测网络；5）TPA-LSTM［21］是一种 注意力 递归神 经网络；6）MTGNN［18］是一种图神经网络；7）AttnAR［23］是一种基于时不变注意力机制的卷积神经网络。

预测时间步与文献［15］保持一致设置为3、6、12和24，时间步越大表示预测时间间隔越长，预测难度也越大。不同模型在各数据集上的测试结果如表3所示，加粗表示最优数据，下划线表示次优数据。所有对比模型的实验结果均来源于原文献。本文模型在Traffic 数据集 上预测 时间步3、6、12、24 的平均RRSE 误差为0.423 2，与AR、VARMLP、RNN-GRU、LSTNet-skip、TPA-LSTM、MTGNN 和AttnAR模型相比，预测误差分别降低0.195 8、0.185 0、0.128 6、0.066 6、0.040 5、0.024 6、0.011 9。FFANet 模型在Solar Energy 数据集上的RRSE 误差平均为0.277 8，相比上述7 种预测模型，预测误差分别降低0.243 0、0.114 3、0.061 5、0.029 6、0.016 5、0.009 8、0.040 0。FFANet 模型在Electricity 数据集上的RRSE 误差平均为0.085 3，相比上述7 种预测模型，预测误差分别降 低0.018 0、0.060 8、0.032 8、0.009 9、0.007 4、0.002 0、0.008 1。

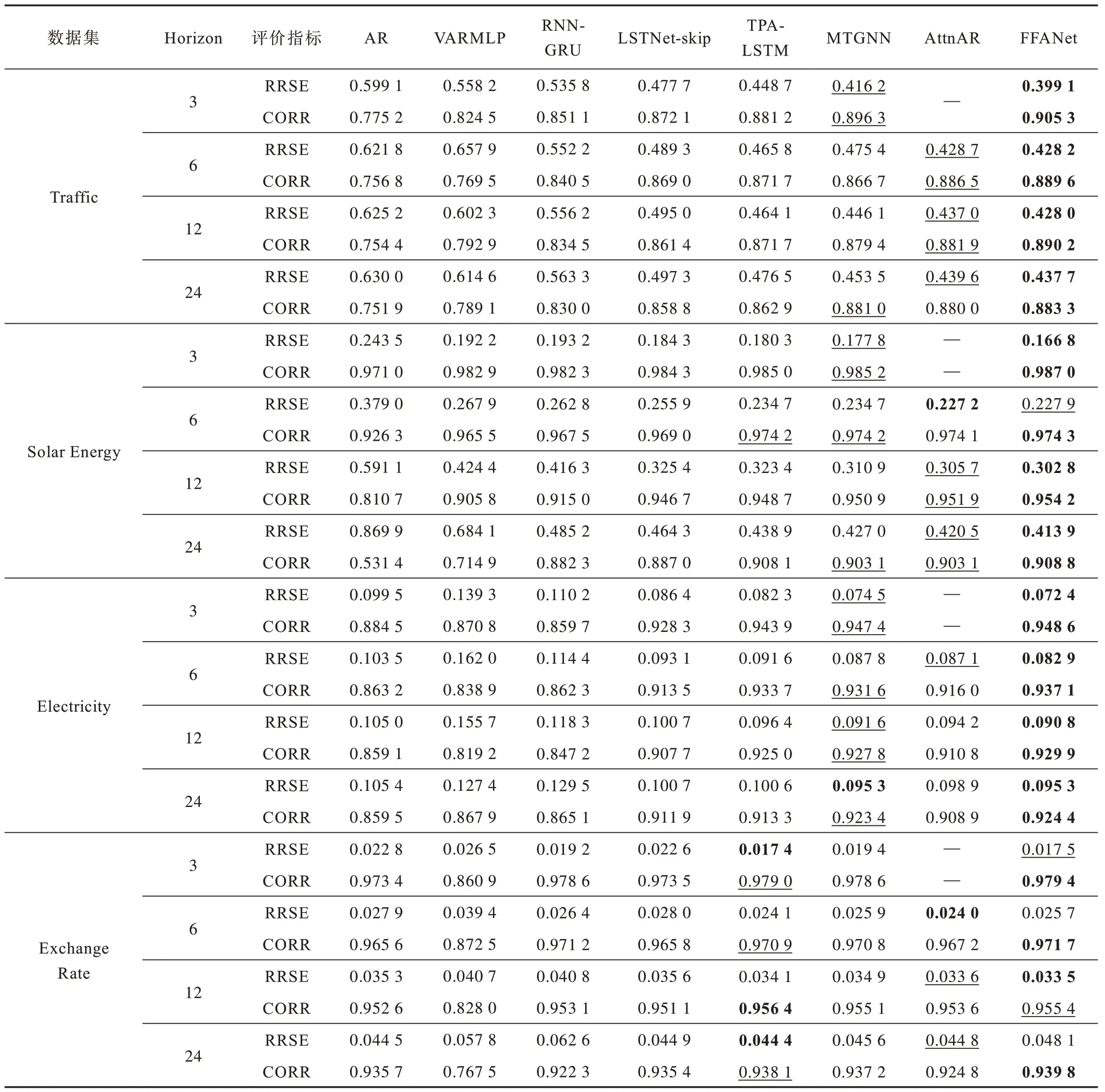
表3 各模型在不同数据集上的预测结果Table 3 Forecasting results of each models on different datasets

相比早期的AR、VARMLP 和RNN-GRU 模型，本文模型在RRSE 和CORR 指标上取得了较大提升，其原因为基于统计的AR 模型无法捕获MTS 数据中复杂的非线性关系，VARMLP 和RNN-GRU 模型只能提取单一尺度时序特征，且无法处理多元变量间的依赖关系，导致预测误差相对较大。LSTNet-skip 和MTGNN 提取时间序列中的多尺度特征，然而，LSTNet-skip 只能处理定长的短期模式和长期模式，MTGNN 则无法自适应融合不同尺度特征。TPA-LSTM 和AttnAR 方法引入注意力机制，然而只从时序维度施加注意力权重，对预测准确率的提升仍然有限。

从表3 可以看出，在Traffic 数据集中，FFANet 模型相比于MTGNN 模型在预测时间步3、6、12、24 上的RRSE 分别降低了4.11%、9.93%、4.06%和3.48%。这是因为Traffic 数据集存在明显的多尺度模式（如小时、天、周等），FFANet 中的多尺度时序特征融合模块能够识别不同尺度模式，双注意力模块对每个变量的时序和通道特征进行聚焦，从而获得更精确的预测结果。在Solar Energy 数据集中各变量数据的夜间读数为0，仅存在小时、天等小尺度模式，因此当预测时间步为3 时FFANet 预测RRSM 最优，相较于MTGNN 降低了6.18%，随着预测时间步的增大，RRSE 分别增大了2.90%、2.61% 和3.07%。FFANet在Exchange Rate 数据集上的预测效果较差，主要原因是Exchange Rate 数据集中各变量变化较随机且不具备多尺度性，无法从中有效提取多尺度特征。此外，FFANet 模型在预测时间步3、6、24 上的CORR指标取得了最高结果，表明双注意力模块能够捕获时序依赖关系及变化趋势。

3.2.2 消融实验

FFANet 模型包括多尺度时序特征融合模块和双注意力模块2 个核心部件，其中，DAM 又包含时序注意力机制和通道注意力机制。为了验证各部件在FFANet 中的有效性，本文设计4 种网络：1）Base 是在FFANet 模型的基础上去除FFM 模块和DAM 模块；2）Base+FFM 是在Base模型的基础上增加FFM 模块；3）Base+FFM+CA 是在Base+FFM 模型的基础上添加通道注意力；4）Base+FFM+TA 是在Base+FFM 模型的基础上添加时序注意力机制。本文选取了Electricity 和Solar Energy 2 个代表性数据集进行消融实验，Electricity 数据集包含多种模式（时、天、周）变化，Solar Energy 数据集的变化主要集中在白天，各变量数据的夜间读数为0。消融实验结果如图4所示。

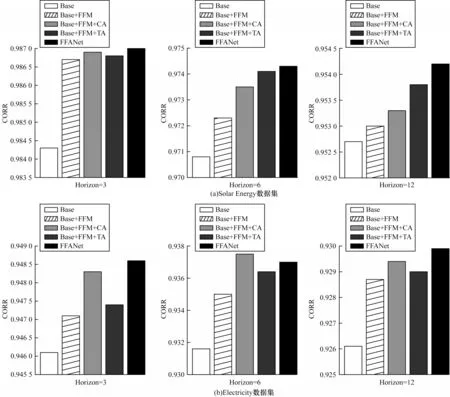
图4 消融实验结果Fig.4 Ablation experiment results

在Electricity 数据集中，随着Horizon 的增加，FFM 模块的作用愈发突显。主要原因是待预测点与输入样本间的模式复杂性随着Horizon 的增加而增加，FFM 模块准确挖掘其中的关联关系，自适应融合跨尺度特征。然而，在Solar Energy 数据集中出现了与之相反的规律，FFM 模块相较于Base 模型CORR分别提升0.002 4、0.001 5 和0.000 3。这是因为该数据集的读数主要与当日天气有关且夜间读数为0，没有明显的多尺度特征，导致FFM 模块作用不显著。

在上述模型基础上进一步增加了TA 和CA，实验结果表明，将TA 和CA 同时加入使模型具有较优的实验结果。此外，在Solar Energy 数据集中注意力机制的作用更明显，尤其是时序注意力机制。时序注意力机制对与待预测点相关的时序特征进行聚焦，从而提升了预测的准确性。因此，在多尺度特征并存的数据中，FFM 模块的效果更显著；反之，注意力机制则占据主导地位。

3.2.3 超参数选择与设置

本文对FFANet 模型中节点嵌入维度e和特征通道数C超参数进行实验，采用贪婪策略确定最优参数组合。给定节点嵌入维度e的取值集合为｛10，20，30，40，50，60｝，特征通道数C的取值集合为｛8，16，24，32，48，64｝。本文固 定C的值为32，分别在Traffic、Solar Energy 和Electricity 数据集上对e的取值进行实验，选取使模型达到最高CORR 值的超参数e作为最优值。将超参数e的最优值固定，从而确定C的取值。每组实验分别进行3 次。图5 所示为在Traffic、Solar Energy、Electricity 数据集上节点嵌入维度e对CORR 的影响。图6 所示为在Electricity数据集上特征通道数C对CORR 的影响。

图5 节点嵌入维度e 对CORR 的影响Fig.5 Influence of node embedding dimension e on CORR

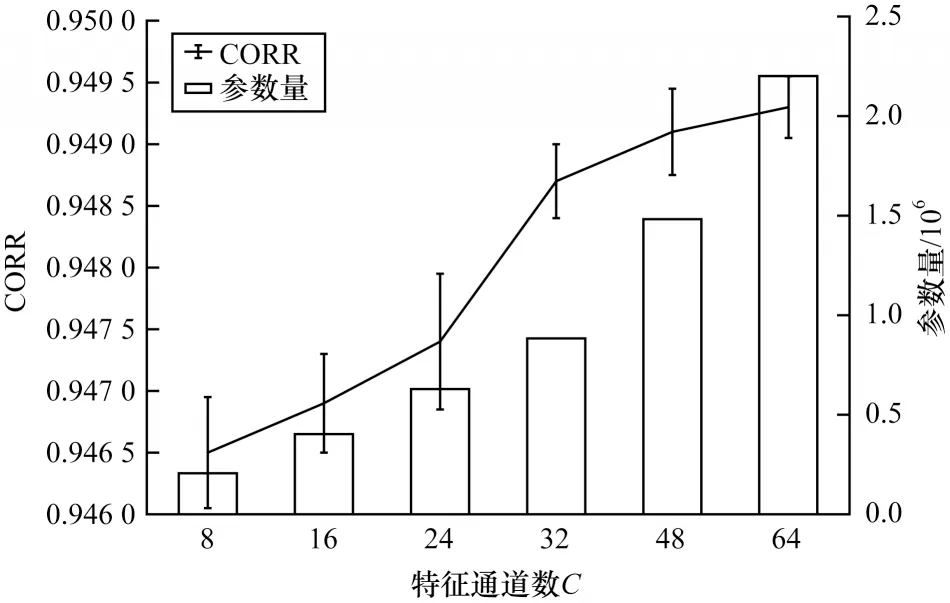
图6 在Electricity 数据集上特征通道数C 对CORR 的影响Fig.6 Influence of characteristic channel number C on CORR on Electricity dataset

从图5 可以看出，在3 个数据集上节点嵌入维度e对模型的影响大致相似。FFANet 模型性能表现随着e的增加呈现出先上升后下降的趋势，说明e在一定范围内的增加使得图邻接矩阵融入更多信息，从而使FFANet 模型表现更优的性能。在3 个数据集上的实验结果显示，当e=40 时FFANet 模型性能最佳。从图6 可以看出，对于特征通道数C，特征数量的增加使得FFANet 模型性能总体表现上升趋势。但是，FFANet 模型参数量也随着C的增加而线性增加，导致FFANet 模型训练会花费更长时间。因此，C=32是更综合的选择，不仅可以取得较优的性能，而且可以节省训练时间。

4 结束语

为提高多元时间序列的预测准确率，本文提出一种基于多尺度时序特征融合与双注意力机制的多元时间序列预测网络FFANet。针对时序数据包含的不同时间跨度特征难以有效利用问题，设计多尺度时序特征融合模块，通过时序膨胀卷积提取数据在不同尺度上的特征，并对其进行自适应选择和融合，从而获得更丰富的特征表示。同时，结合双注意力机制，从时序及通道维度分析相关特征的重要性，进而聚焦其中重要部分，提高模型预测精度。在Traffic、Solar Energy、Electricity 和Exchange Rate 4 个多变量时间序列数据集上的实验结果表明，本文方法与当前主流的时间序列预测方法相比，在RRSE和CORR 指标上取得了较优的预测效果。下一步将在本文所提模型的基础上深入研究动态图结构，通过动态更新图邻接矩阵以建模各变量间的时变相关性，提高变量间关联分析能力。