结构钢试件不同载荷下断铅声发射信号的混沌特征＊

刘婷，张堃，郭晓艳

（中山火炬职业技术学院，广东 中山 528437）

Q235 钢是一种碳素结构钢，由于它含碳适中，综合性能较好，因此无论是在建筑、工程结构中，还是在机械零件中，Q235 钢都有很大的需求体量。也正因Q235 钢应用的广泛性，在实际的工程应用中，对Q235钢内部损伤程度进行无损检测，无论在事故预防，还是在旧零件再制造等方面都具有极其重要的意义[1]。现在常用的无损检测方法有很多，如超声检测、电磁监测、声发射检测、红外检测等，而在诸多无损检测方法中，声发射检测技术因其灵敏度高、抗干扰能力强等优点，日益成为无损检测方面的研究热点[2]。

张颖等[3]对由Q235 钢可视化原位拉伸实验所获取的声发射源信号进行了分析，根据声发射源动态观察结果及图像分析，建立了Q235 的声发射细观损伤模型；陈冰等[4]通过时频特征分析在声发射信号中提取带锯条全生命周期的磨损信号特征，判断带锯条的初始剧烈磨损时间；毛汉颖等[5]通过断铅声发射信号，估算金属材料的声阻抗值，表征了金属材料的损伤程度；贺秀丽等[6]利用声发射技术对镁合金进行监测，分析了在腐蚀及疲劳载荷等不同情况下的声发射波形特征；綦磊等[7]以声发射技术为基础，采用混沌-BP 神经网络相结合的方法，实现了泄漏检测及对漏孔大小的评估。

为了有效分析Q235 钢金属材料内部损伤程度，基于金属材料损伤非线性的特点，本文首先对不同损伤情况的Q235 钢进行断铅声发射试验，激励其内部损伤特征，获取断铅声发射信号；然后采用混沌分形理论对获得的断铅声发射信号进行特征分析，通过计算不同损伤程度下的结构钢的声发射信号的关联维数、最大Lyapunov 指数及Kolmogorov 熵值，进行综合比较，以期检测出声发射信号中的损伤信息，从而实现对金属材料内部损伤程度的判断。

1 断铅声发射试验设置

试件采用尺寸为210 mm×30 mm×1 mm 的Q235钢材料，为了模拟损伤状态，对所有钢材进行拉伸试验，最大拉力分别设为0 kN、4 kN、8 kN、12 kN、14 kN。受到5 种不同级别的最大拉力的试件，分别用于模拟5 种不同损伤程度的损伤试件。

本试验平台采用美国物理声学公司（PAC）生产的PCI-II系统进行断铅试验：在试件的一端放置传感器，试件另一端设置断铅点，位置如图1 所示。试验中，使用HB 铅笔，保证其与试件表面成30°夹角，均匀用力压断铅芯，采集产生的声发射信号。

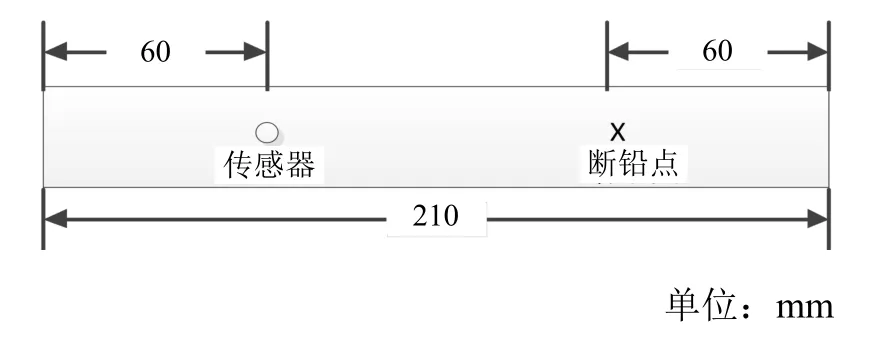
图1 试件示意图

分别对先前制备的5 种不同损伤程度的试件进行断铅试验，断铅产生的声发射信号沿试件传递，经过损伤部位后被传感器接收，记录声发射信号数据。为减少误差，对每组试件分别进行5 次试验后，取获得的数据的平均值进行后续分析。

2 混沌特征量算法

2.1 关联维数

在机械故障诊断中，经常用关联维数[8-10]来定量说明系统的复杂程度，这是机械故障诊断中一种重要的方法。

关联维数有多种计算方法，本文采用G-P 算法进行计算：首先对原始时间序列进行相空间重构，取该相空间中的一个相点为中心，计算相点落入超球体之内的概率，即关联积分为：

式中：m为相空间重构中的嵌入维数的数值；N（m）为重构向量的个数；r为超球体半径的数值；H为Heaviside 函数。

Heaviside 函数的公式为：

将r适当缩小，根据关联积分与r的关系式，可得：

式中：d为关联维数的数值。

关联维数d的公式为：

如果关联维数随着嵌入维数m的增加而不断增加，则表示数据为随机序列；如果关联维数随着嵌入维数m的增加而增加，最后无限趋于饱和，则表示为混沌序列。

根据G-P 法获得关联维数的计算结果，如图2 所示。首先对lnC（r）-lnr曲线（如图2（a）所示）中的直线段部分进行最小二乘拟合，即可求得每条直线段的斜率，结果如图2（b）所示。关联维数d即斜率随m的增加而趋向饱和的那个值。

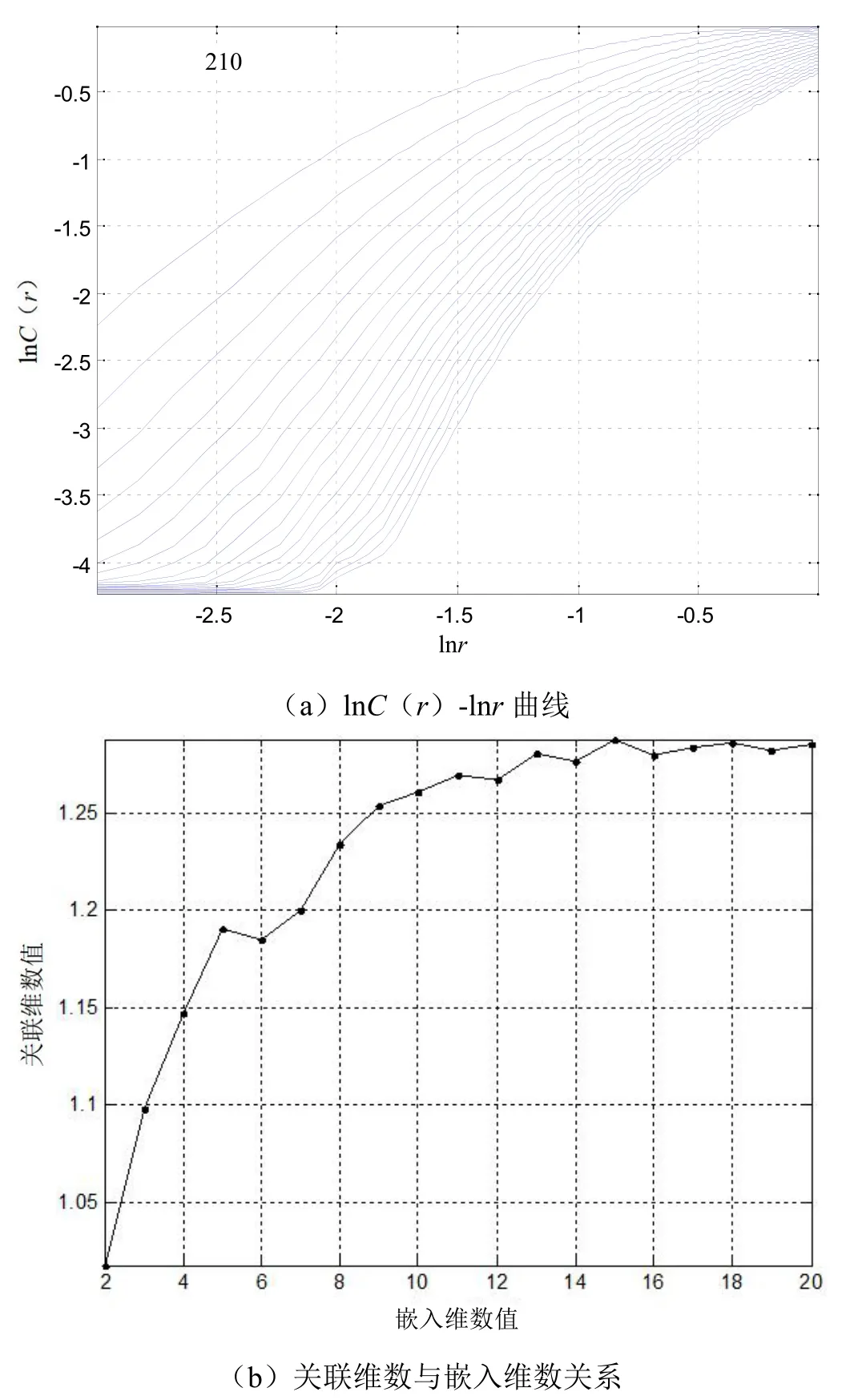
图2 关联维数计算过程

从图2（b）的曲线中可以看出，一开始，斜率随m的增加而增加，当m增加到14 之后，斜率变化变成在一定的区间内波动，并且逐渐平稳，趋于饱和。此时，对平稳区间内的斜率取平均值，即得到时间序列的关联维数为1.28。

同理，可以计算得到其他不同损伤程度的试件的信号的关联维数值，从而得到不同损伤程度下的试件的声发射信号的关联维数的变化趋势，如图3 所示。

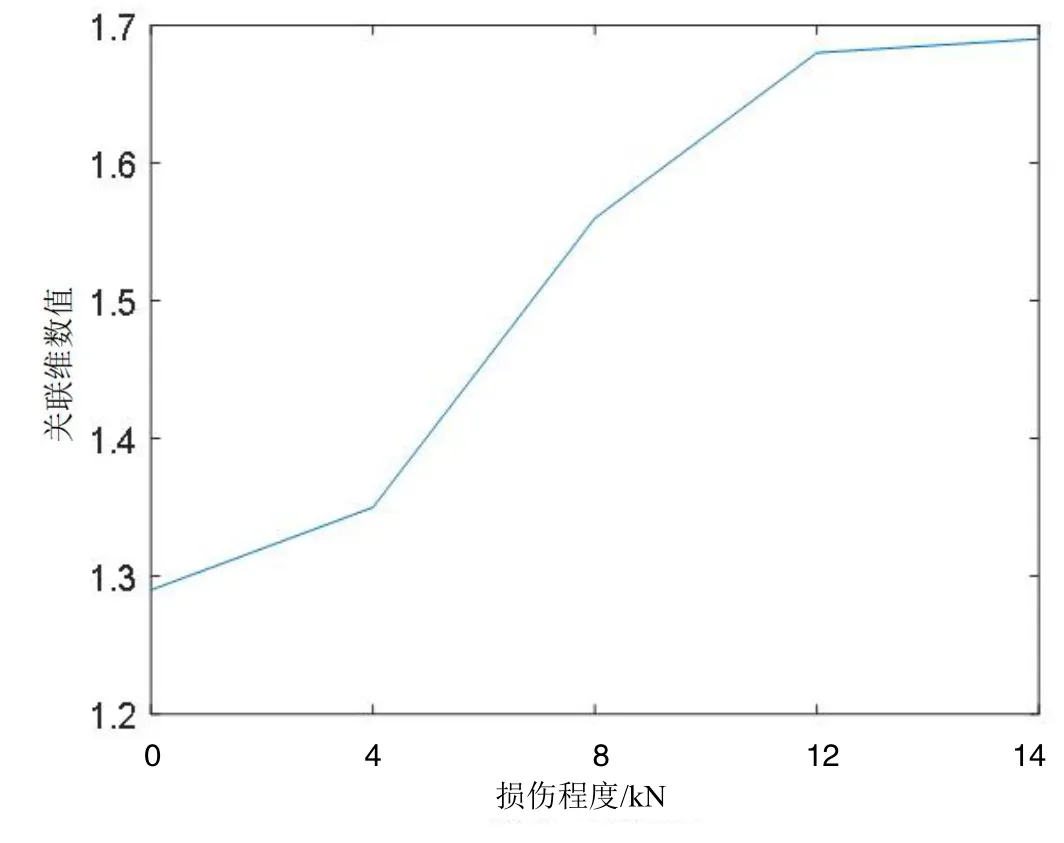
图3 不同损伤程度下的关联维数值

2.2 最大Lyapunov 指数

Lyapunov 指数是相邻相空间轨道按指数发散或收敛的速度的一种定量描述，本文采用小数据量法计算各损伤程度下时间序列的最大Lyapunov 指数值λ1[11-12]。首先在重构的相空间中计算第j个参考点Xj与最近相邻点Xjˆ之间的初始距离dj（0），即：

式中：p为时间序列的平均周期的数值。

计算出各参考点Xj与最近相邻点Xjˆ的第i个离散时间步长后的距离dj（i），即：

这里假设参考点Xj与最近相邻点Xjˆ具有λ1的指数发散率，根据上式计算可得到：

利用最小二乘法拟合y（i）曲线中的线性区域即可得到最大Lyapunov 指数值λ1。如果最大Lyapunov指数值大于0，则判定系统混沌，并且最大Lyapunov指数值越大，系统越混沌。

以无损条件下试件为例，其最大Lyapunov 指数值的计算过程如图4 所示。根据小数据量法，用最小二乘法对y（i）曲线的线性部分进行拟合，得到的斜率就是此时的最大Lyapunov 指数值，为0.012 4。同理，可以得到其他几种不同损伤程度下试件的声发射信号的最大Lyapunov 指数值，其变化趋势如图5 所示。

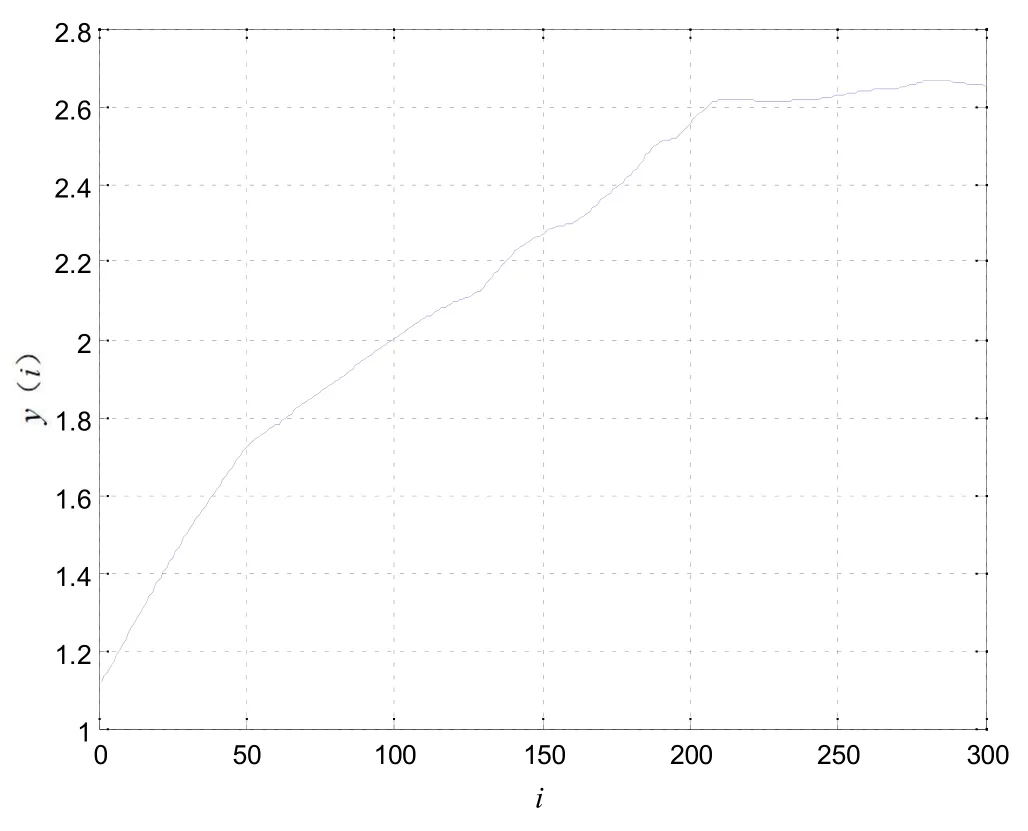
图4 最大Lyapunov 指数值的计算过程

图5 不同损伤程度下的最大Lyapunov 指数值

2.3 Kolmogorov 熵

Kolmogorov 熵（以下简称“K 熵”）是表达混沌系统的一个非常重要的量，它反映了系统的混乱度，其数值根据不同类型的动力学系统而不同：若K 熵的值为0，则系统为规则系统；若K 熵的值是无界的，则系统为随机系统；若K 熵的值大于0 且有限，则系统为混沌运动系统，并且K 熵值越大，信息损失速率越大，系统的混沌程度越高[13]。

本文根据最大似然法计算各组不同损伤程度下试件的声发射信号的K 熵，得到的结果如图6 所示。

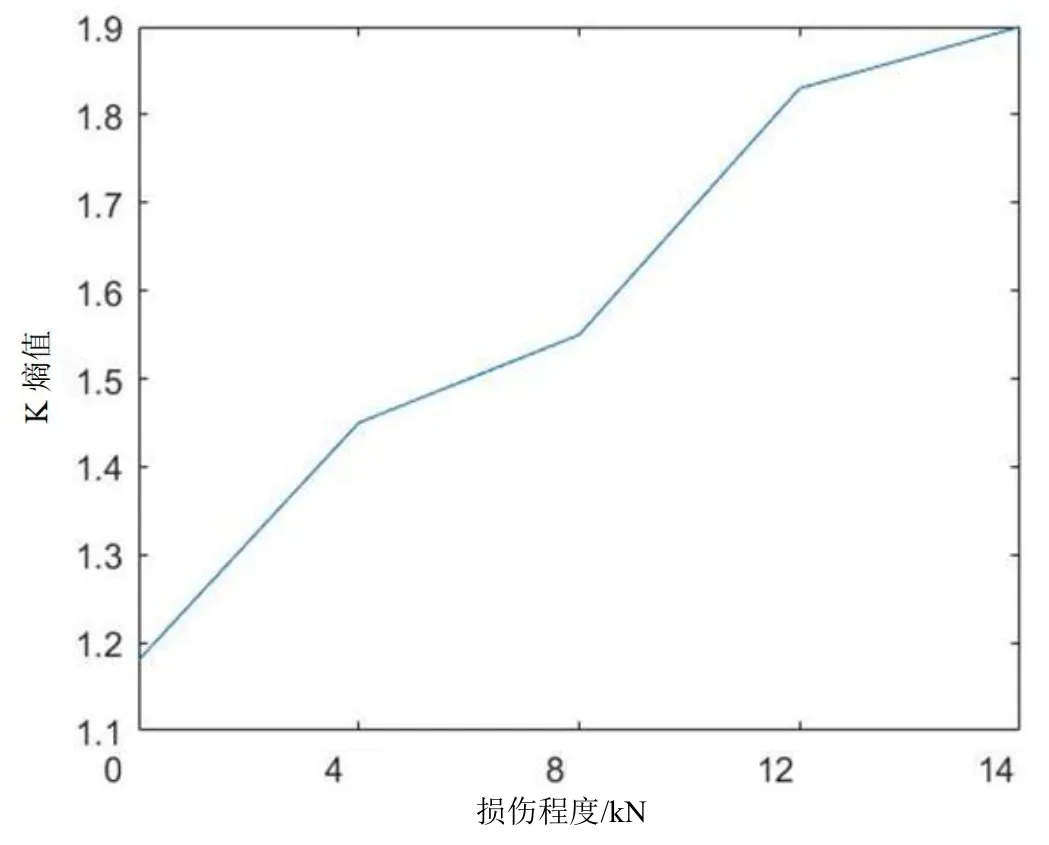
图6 不同损伤程度下的K 熵值

3 断铅声发射信号的混沌特征分析

由上述计算结果显示，采集到的不同损伤程度的试件的声发射信号时间序列均具有正的最大Lyapunov指数，并且关联维数都能够达到饱和状态，表明采集得到的声发射信号时间序列具有混沌特征。

为了便于分析，将上述计算得到的3 种混沌特征量的值进行归一化处理，并绘制趋势图，如图7 所示。

图7 归一化特征值

从图中可以看到，随着试件损伤程度的增加，3种混沌特征值都呈上升趋势，不难分析，随着试件所受拉力的增加，试件的损伤程度不断增大，大量的微裂纹开始发生萌生，并且不断扩展，导致试件的非线性程度不断增加，所以混沌特征值也随之不断上升。

同时可以发现，在模拟试件损伤前期（所受拉力为0～8 kN 时），关联维数的增幅相较其他2 种混沌特征值更明显。分析可知，此时的试件处于拉伸变形的弹性变形阶段，微裂纹开始萌生，试件内部复杂程度高，而关联维数正好能够很好地描述系统的复杂程度，因此该值的增幅程度相对较大；在模拟试件损伤中后期（所受拉力为8～12 kN 时），试件处于拉伸曲线由屈服阶段到塑性变形阶段的过程中，分布不均的微裂纹大量萌生和扩展，此时可以发现最大Lyapunov指数的增幅更大，说明Lyapunov 指数对金属材料内部损伤的发展阶段更加敏感；在模拟试件损伤后期（所受拉力为12～14 kN 时），试件到达塑性变形阶段，发生形变并趋于断裂，此时内部裂纹扩展大小方向趋于统一，混沌特征量也趋于饱和，其变化幅度不再像受损伤前中期那样剧烈，而是逐渐趋于平稳。

4 结束语

为了实现对金属损伤程度的判定，本文通过利用Q235 钢进行声发射断铅试验，激励对其内部损伤进行混沌特征量分析，得到以下结果：①试验结果表明，随着试件损伤程度的增大，混沌特征值也增大。因此，通过声发射信号计算得到的关联维数、最大Lyapunov指数、K 熵的值与结构钢试件的损伤程度呈正相关关系，这3 种混沌特征值反映了结构钢试件内部的复杂性和无序性，其变化趋势能够在一定程度上对金属材料损伤程度进行表征。②不同损伤程度下试件的声发射信号所对应的混沌特征值敏感程度不同。不难发现，试验结果中计算得到的关联维数对结构钢试件内部发生损伤的萌生阶段更敏感，而在结构钢试件内部损伤的发展阶段，最大Lyapunov 指数的增量更明显，因此，不同损伤阶段的结构钢利用不同的混沌特征值能够更好地实现损伤程度判定。③通过试验证明，断铅声发射信号能够激励结构钢内部的损伤信息，并且结合结构钢声发射信号的多个混沌特征值，可以从不同角度来实现对结构钢损伤程度的共同判定，为金属损伤程度判断奠定了基础，并且为金属损伤识别的应用方面提供了一定的试验依据。