Lyapunov 稳定性分析在欠驱动船舶路径跟踪的应用
2023-09-16夏云青
夏云青
(郑州工程技术学院 基础科学学院,河南 郑州 450044)
0 引 言
为了实现对运动目标的跟踪,运动目标检测环节绝对不可缺少,以及最后检测结果的可靠性,会对目标跟踪的精度造成直接影响。因此对于运动目标的相关监测工作,必须采用有效的手段。以船舶欠驱动系统控制为例,对其进行路径跟踪的相关研究中,应以鲁棒性为主线,完成运动目标检测计划的制定。而在关于控制系统稳定性的研究进程中,不同的学者基于不同的模型,从多角度对非线性系统的特征值分布提出了各自的理解以及研究成果,李雅普诺夫基于前人研究,由此归纳了Lyapunov 稳定性理论,为状态方程的求解提供了宝贵的建议。而本文选取的Lyapunov 稳定性理论,特指Lyapunov 第二方法,Lyapunov 直接法[1-2]。
所谓运动目标检测问题,即能对系统中运动目标所呈现的运动特征和运动目标本身特征做科学分析,以及对于视频序列图像的综合检测问题,若存在这种地区,该系统可以执行分割提取操作,使得视频序列中图像背景可以跟随它的相对运动区域而独立分开[3-5]。
基于此,本文以欠驱动船舶路径跟踪为研究对象,对其应用可行性以及局限性展开分析,并搭配以背景减除法作为视频中运动目标安全检测方法,通过完整检测流程并结合Lyapunov 稳定性理论,为实现运动目标跟踪打下研究基础,以期在欠驱动船舶路径跟踪检测结果的可靠性上,可以对目标跟踪的准确性带来直接影响,从而为船舶领域的非线性系统稳定性研究提供一定的依据。
1 Lyapunov 稳定性理论基础
以欠驱动船舶路径跟踪为研究对象,围绕其二维非线性系统进行研究,设Lyapunov 稳定性微分方程如下:
由此导出船舶经欠驱动系统控制输入后,其运动路径的微分方程:
计算船舶经欠驱动系统控制输入后,其运动路径的速度沿二自由度系统方程展开曲线求解,得出:
由此得出,Lyapunov 稳定性理论在实际应用中具有一定的可操作性,但同时也存在局限性。因此合理对其进行优化,并在应用中进行测试,将是接下来探讨的方向。
2 基于Lyapunov 稳定性理论的欠驱动系统控制
2.1 核带宽自适应调整
该系统采用Lyapunov 稳定性理论,实现迭代搜索操作,以及对运动目标进行最佳位置检测,基于该系统可以利用图像目标区域投影完成二维概率密度分布图,并计算系统中概率密度的零阶矩。该算法可以根据不同场景和环境中出现的情况自动选择合适的概率值,从而提高整个系统对复杂背景下运动目标的定位速度。计算公式为:
式中:I(x,y)为图像目标在(x,y)坐标时对应的概率密度估计值,并且x值以及y值都要在核函数带宽所支持的船舶范围完成取值。
2.2 视频目标跟踪
由于视频运动的对象不一样,产生了种种行为特征,并且在目标跟踪时也会面临变幻莫测的问题,加之为了保证视频运动目标跟踪的实时性和鲁棒性,需要对各种运动目标跟踪算法进行研究,具有代表性的运动目标跟踪算法包括:
1)轮廓跟踪算法。该算法的指导思想即以系统内的运动目标为中心,以及将它们的外边缘轮廓布置为目标模板,基于该系统,可利用定位检索的方式形成目标轮廓模板综合跟踪。随着相关技术的发展,该模型在军事领域又进一步完成主动轮廓线跟踪算法研究和开发,后期算法应用于智能监控,从而为军事科技、航海航空等领域在视频处理方面取得了重大进展与应用。
2)区域模板跟踪算法。采用区域模板跟踪算法对目标进行跟踪,可以把整个目标模板都反馈到系统中,也即是对系统能有一个比较全面的认识、材料更加多样化。本文通过对区域模板跟踪算法原理与应用方法的分析,提出了基于该算法的运动补偿技术。该算法常被用于弱对比度目标和小目标的综合跟踪工作,且性能突出,普及度较高。该算法通过对多个图像数据集分别采用不同大小的子图进行匹配处理来完成目标识别和跟踪器的建立。
3)特征数据匹配算法。该算法指导思想是在系统内能够使用包括边缘特征、目标角点等部分特征数据用于模板设置,基于此系统可以利用特征数据进行匹配检索操作,由此达到对运动图像序列进行综合跟踪的效果。
2.3 多特征自适应融合的Lyapunov 稳定性分析
推动Lyapunov 稳定性理论与多特征自适应融合法兼容合作,能保证系统描述目标模型时,即便受到场景变化的干扰或者是目标变化的干扰也依然能表现出适应性、鲁棒性。
如图1 所示,本文提出一种基于动态阈值与核参数相结合的方法,来抑制图像中背景噪声及前景目标区域的影响。据此,为了可以对Lyapunov 稳定性理论应用于欠驱动船舶路径跟踪加以优化,本文利用纹理特征、颜色特征完成目标模型创建,并以此为基础,采用多特征跟踪算法,便于与目标模型和候选目标模型进行兼容与合作。
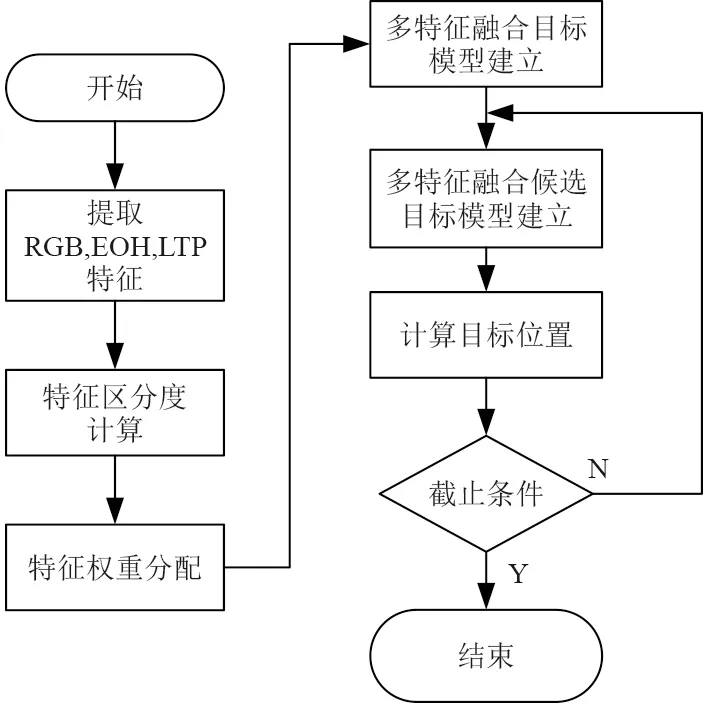
图1 多特征融合算法流程图Fig.1 Flow chart of multi feature fusion algorithm
假设y0为候选目标所处的位置,该算法将使用以下公式进行计算:
其中,i=1,……nk
在上述公式中以权重值为判断依据,完成对运动目标实时位置的计算,可以得到最新的位置权重值为

此外,若欠驱动船舶路径跟踪视频序列没有结束,则系统会继续对图像序列进行读取操作,并在系统内对下一帧图像启动目标跟踪操作。
2.4 跟踪算法的实现
基于以上研究,对欠驱动船舶路径跟踪特性进行自适应分析,并融合了Lyapunov 稳定性理论进行更加细致的描述。
步骤1 使用前面探测运动目标得到的初始化数据进行初始化;
步骤2 在设置目标模板过程中采用背景加权完成目标模板刷新程度的选择;
步骤3 通过卡尔曼算法,得到预估值yo,然后用所设门限值α与Mean Shift 收敛值y1比较,即若造成遮挡范围大的情况,能用预估点位数据刷新。
步骤4 当欠驱动系统控制预估点位的偏差值比较大时,则步长为1.5 倍核带宽,在欠驱动系统控制预估点位进行初始化操作,检索成果即为最小的迭代点位。
步骤5 最终判别追踪区间内目标存在与否,如果不存在,算法完成;反之,在下一帧进行研究。
最终得到两运动目标融合再分离的结果,在此实验基础上得到了一种可以用于实时监控系统的视频压缩方案。生成监控画面中的2 个运动目标,同时完成追踪效果。进而实践证明,本文采用Lyapunov 稳定性理论能够在欠驱动船舶路径实现完美跟踪。
3 算法的实际应用结果分析
本设计系统采用了改进的Lyapunov 稳定性理论进行目标跟踪,能够加强运动目标探测的精确性、鲁棒性、可靠性和高效性。
如图2 所示,X轴跟踪误差表现为视频序列尾部出现算法分离,在背景受到扰动时或者目标形态发生改变时,该系统采用经典Lyapunov 稳定性理论对目标跟踪,造成跟踪错位。针对以上存在的缺陷,本文提出一种基于图像特征匹配技术和自适应滤波相结合的方法。据试验得知:与经典的Mean Shift 的目标跟踪算法相比,该系统采用改进的Lyapunov 稳定性理论对目标进行跟踪,将更具有可靠性,鲁棒性和精确性。
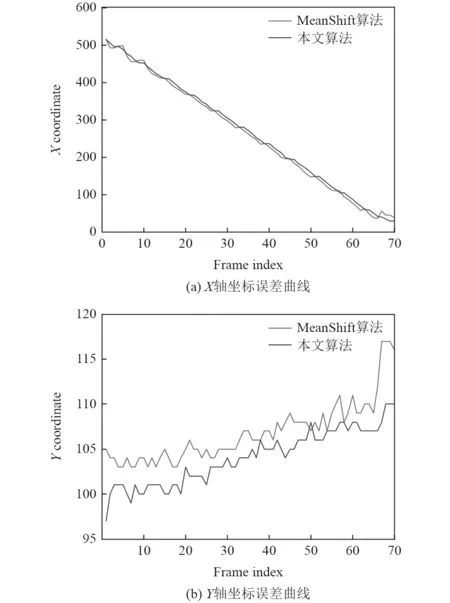
图2 欠驱动船舶跟踪误差分析图Fig.2 Analysis of tracking error of underactuation ship
如图3 所示,选取一段真实场景视频作为研究对象,按数量划分,检测人员进行了仿真,并对初始目标区域进行设定和分割;当需要进行自动追踪时,则需要利用摄像机采集到的原始图像信息来确定最终位置,然后通过计算获得移动方向和速度等参数后实现对欠驱动船舶的准确定位,并通过Lyapunov 稳定性分析欠驱动船舶路径跟踪的准确性,从而弥补了该理论研究的局限性。
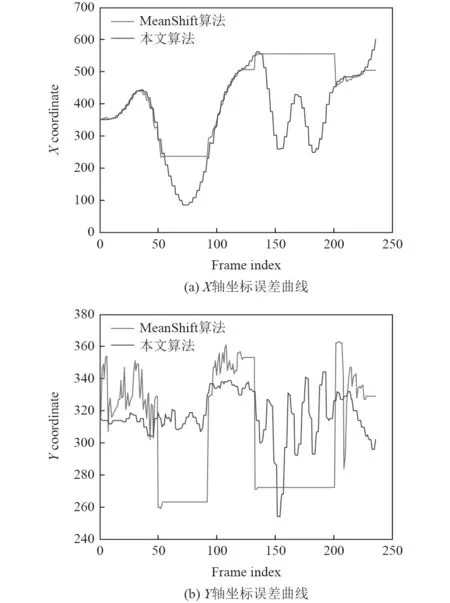
图3 欠驱动船舶路径跟踪误差场景分析图Fig.3 Scenario analysis of underactuation ship path tracking error
同 时,本 文 采 用Microsoft Visual Studio 2017 技术,完成了程序运行环境构建。通过以上步骤,能够实现对于被测船舶欠驱动系统控制特征的准确提取,以此为后续研究提供参考依据。不同测试条件下的跟踪算法的比较如表1 所示,该表反映了综合欠驱动船舶路径跟踪的性能水平。
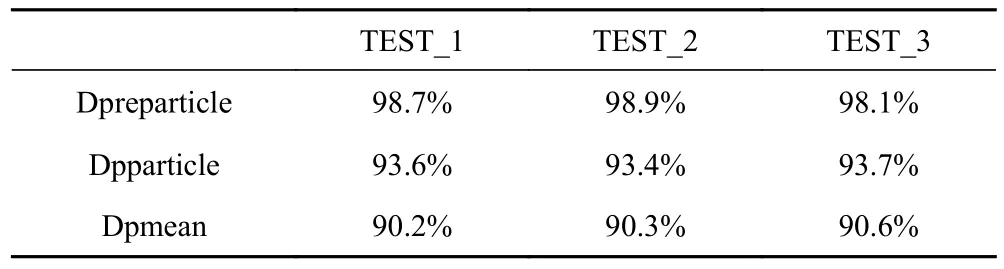
表1 不同测试条件下的跟踪算法比较Tab.1 Comparison of tracking algorithms underdifferent test conditions
其中,Dpreparticle 表示以小波特性为核心的粒子滤波跟踪算法;Dpparticle 表示以特征值H 为核心的粒子滤波跟踪算法;Dpmean 表示以特征值H 为核心的均值滤波跟踪算法。被测试的录像是单船舶测试录像,视频时间应保持在20 s 之内,视频码率应在30 帧/秒以上,且检测次数应在3 次以上,检测船舶经欠驱动系统控制后,其对于帧数进行了统计。此外,将Dpreparticle 算法分别与Dpparticle 算法、Dpmean 算法进行对比,得知,Dpreparticle 算法更具有精确性,并且其性能也比其它两种算法高出大概3%~5%。
4 结 语
本文结合当下船舶行业发展趋势,基于Lyapunov的稳定性理论对欠驱动船舶的路径跟踪算法进行了深入研究,并将多特征自适应融合算法与路径跟踪过程结合,优化了视频自动路径跟踪的效果,测试结果表明该算法能够降低位置跟踪误差,能够显著提高欠驱动船舶路径跟踪的准确度,具备广泛的应用前景。
