超大型集装箱船中横隔板拓扑优化方法研究

李海洲，李小灵，童晓旺，李安琪，刘 平,

(1.江南造船(集团)有限责任公司，上海 201918；2.江苏科技大学 土木工程与建筑学院，江苏 镇江 212003)

0 引 言

优化设计思想很早就有学者提出，早在20 世纪60 年代，优化设计方法正被一些学者应用于机械、飞机制造、船舶工业等领域。1986 年，Moe 等[1,2]阐述了关于运输船甲板的优化计算方法，并第一次在船舶结构领域应用了数学规划理论。这项研究成果标志着船舶结构设计进入了优化思想阶段[3,4]。随着半个世纪的发展，针对舱口形状等局部结构的尺寸优化和拓扑设计已经较为成熟[5,6]。Michael[7]对船体的早期阶段设计优化进行了研究，表明在早期阶段考虑船体的优化可最高节约15%的建造成本。2012 年，Ling Cao[8]提出了一种新型拓扑优化算法，并成功应用于船体的横梁剖面。几何优化的基本思想是以材料分布作为优化变量，基于优化对象设定约束条件，然后通过特定算法，找到最优的分布方案[9,10]。目前，在连续假设基础上兴起的拓扑优化理论被广泛应用于航天工程、机械制造、汽车工业等领域，也被少量应用于船舶行业[11-13]。但是，关于船舶构件拓扑与尺寸优化分析的实际应用非常少。

Masafumi 等[6]研究了发动机振动下的船甲板拓扑优化问题，采用多尺度优化策略来分析结构的振动控制，结果表明，通过对船体甲板的拓扑形状进行优化，噪声平均可以减少8%。SÖĞÜT 等[14]对船体的拓扑设计与能耗进行研究，结果表明优良的拓扑形状在正常航行状态下可节约5.7%的能耗。孙志军[15]提出了一种基于拓扑优化技术进行船舶机舱发电机的抗振加固研究，结果表明在减少1.2 t 重量的情况下，振动效应减少约6%。钦伦洋[16]应用变密度法拓扑优化理论，采用Ansys WORKBENCH 对设计区域进行优化计算，并研究了船舶结构的轻量化问题，结果表明，在不降低结构强度前提下，船体舱壁的结构用材料最高可减少到原来的50%。张会新[17]利用拓扑优化方法对船体的振动特性、声学性能进行评估，结果表明，在不改变声学约束的情况下，船体振动性能改善有限，但是优化后的重量可减少16%。吴贝尼[18]以船体横剖面为研究对象，研究了多种插值函数的效能，并编程实现了拓扑优化，结果表明，G-BESO 方法最为有效，效能最高。

本文在大型集装箱船设计初始时假定中横剖面为矩形板壳结构，然后计算其优化结果。探讨结构形状以及拓扑优化方法在船舶领域中的应用前景，并根据实际工程需要及限制条件，给出了优化模型和优化对象的具体拓扑形状。

1 船体板架结构力学分析模型

某大型箱船结构构件主要包括外甲板、纵骨和横舱壁以及相关附属结构。大型箱船船体外围尺寸和主要设计尺寸如表1 所示。

表1 箱船主要尺寸Tab.1 Main dimension of container ship

本计算采用的箱船坐标系统定义如下：船长为X轴，方向为船行进方向相反；型深方向为Z轴，正方向与重力方向相反；甲板船宽方向为Y轴，正方向由右手坐标系决定。计算模型选取则综合考虑了计算量与简化模型精度的平衡。在实际计算时，在X方向选取了6 个舱段长度，6 个舱段可以充分隔离中横隔剖面边界效应的影响。而在船宽方向选取5 个纵骨间距，这样优化结果基本上与边界效应无关。计算几何模型尺寸为：标准纵骨之间距离为0.75 m；标准舱室间距为4.5 m；纵骨腹板厚为12.5 mm；外甲板厚度为17 mm而横舱壁厚为12.5 m。在甲板层，纵骨面板厚度为36 mm，大肘板厚度为12 mm 而小肘板厚8 mm，扶强材厚10 mm，某超大型箱船横隔舱布置如图1 所示。计算箱船用材料为普通钢，其力学特性参数如表2所示。在计算中采用弹性方法进行计算，不考虑材料的塑性性能。

表2 材料计算参数Tab.2 Material calculation parameters

2 重量目标下船体板架尺寸和形状

2.1 变密度优化方法

将优化对象的密度设定为设计变量，并将其值限定在[0,1]之间，其中：0 表明材料为空；1 表明材料为真实保留。同时，将材料本身的物理属性与单元密度之间按某种函数关系相联系。这样，把真实结构的拓扑优化问题转化为材料密度分布的数学问题。具体的，把物理问题转换为数学问题：

由上述计算过程可知，在优化结束后，单元密度为0 或1 最好，为了实现这种目的，在变密度法引入了罚函数，即在迭代计算中对单元密度乘以常罚函数，使单元密度趋向于0 或1。如图2 所示，惩罚因子为2 时，迭代次数与材料密度分布关系图。实际上，这种函数是在迭代时使得中间密度向0 与1 状态两侧靠近，迭代次数越多，处于中间值（ 0 ＜ρi＜1）的密度单元则越少，从而拓扑优化模型则越接近于0～1 状态。

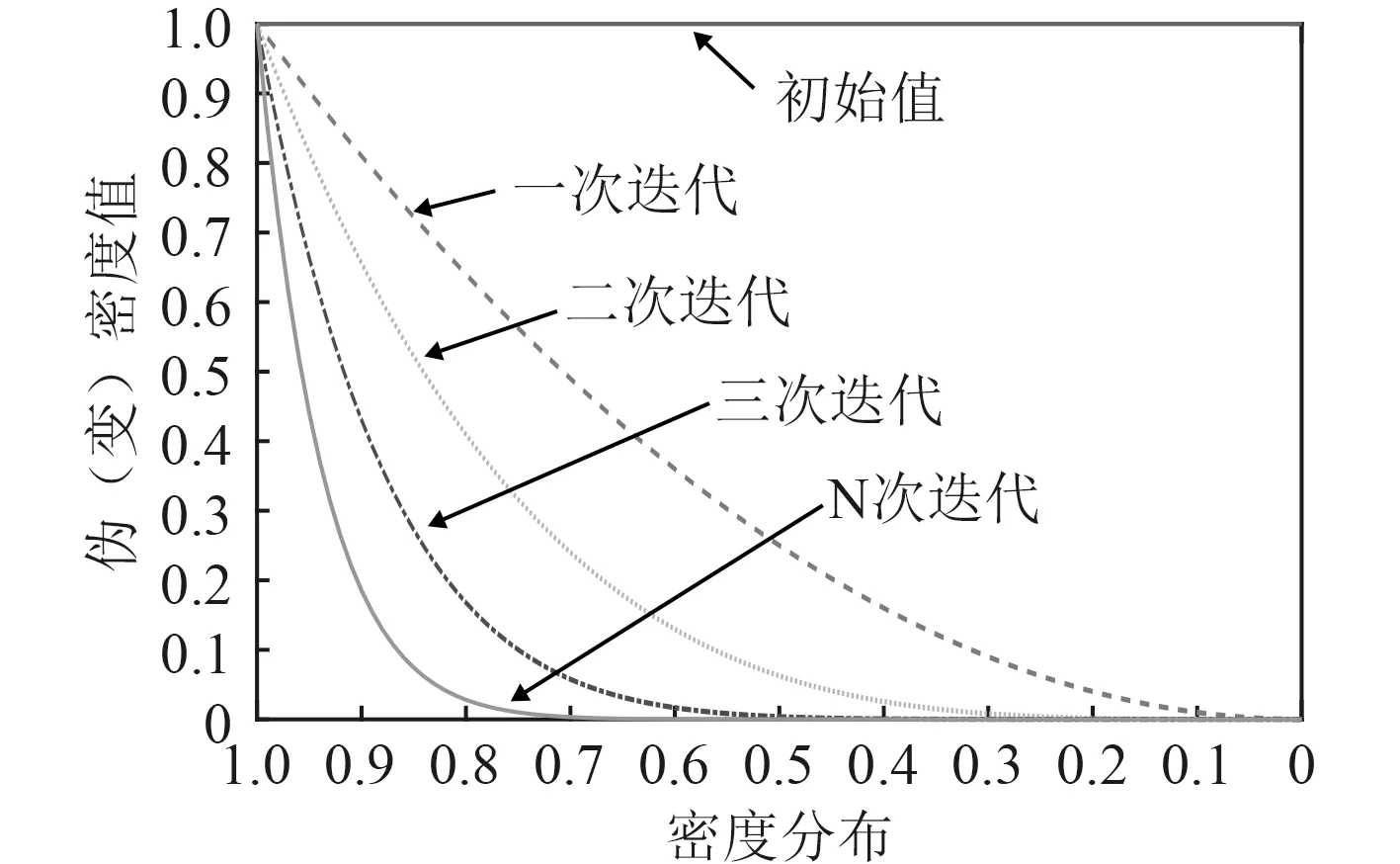
图2 罚函数迭代次数-变密度分布图（惩罚因子取2）Fig.2 The curve of iteration number vs density (penalty number=2)

约束条件方面，在弹性设计分析时，一般取在满足结构刚度的条件下，使所有的单元应力值满足σi＜σs， σs为材料允许应力，即船体所有位置应力均不超过材料的设计强度值。

2.2 结构计算模型

本计算的目标是确保满足应力约束条件下（结构最大应力不超过材料屈服强度）使得结构重量最小，从而实现最优化的经济效益。位移和载荷边界条件如下：

1）载荷工况

板架结构所承受的外荷载主要包括结构自重、水体浮力以及弯矩。由于船舶上建部分在有限元模型中没有体现，因此以荷载的形式加载到横隔板上部；船轴方向的总纵弯曲取200 kN·m，分别加载到横隔板上；水压力取水线在20 m 位置，加载图3 所示。

图3 水浮力及荷载加载图示Fig.3 The load schematic

2）边界条件

船体在水中漂浮时重力与水浮力平衡，实际上没有固定约束。为了在有限元中能够进行分析（为约束刚体位移），采取了“弱弹簧”技术进行处理，弹簧刚度取1e-6 N/m。在实际计算中，读取弱弹簧的反作用力，取实际作用力的1/1000 以下作为依据。

船舶设计经济化是最自然的目标，即使船体结构质量最小为优化目标函数。本计算采用Ansys WORKBENCH 软件进行拓扑优化计算。单元尺寸取0.3 m，四边形网格为主，共有116 134 个结点，122 426 个网格。网格质量分布如图4 所示，可以看出，网格质量较好，有限元计算结果可信。优化分析采用如下约束条件进行计算：①结构的最大等效应力不大于材料的屈服强度，即结构应力不大于215 MPa；②中横隔板的几何形状约束，确保优化后横隔板几何形状对称，即中横隔板符合生产和施工工艺的要求。

图4 单元质量分布图Fig.4 The metric of mesh

3 优化过程

在开始优化过程之前，首先对箱船结构进行静力分析，这样对船体结构的力学状态有初步了解，同时也可对优化结果有初步预判。

3.1 静力分析

在优化计算前，首先对板架结构进行静力分析，其典型等效应力如图5 所示。结构大部分区域的等效应力值均小于203 MPa；此外，应力最大值出现在中横剖面下部左下、与右下位置，中间部分应力较小。由此可见，中间部分结构所用材料并没有得到充分利用，有较大的减重潜力。可看出，约束条件为满足强度条件时，可有更好的空间材料分布。利用 Ansys WORKBENCH Topology 模块对构件进行拓扑优化分析。

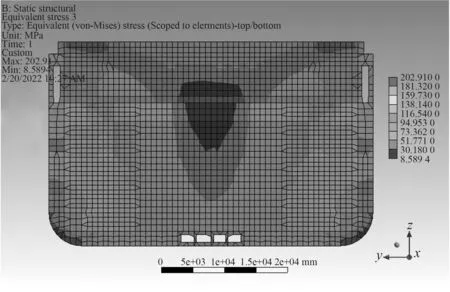
图5 静力分析时的等效应力大小Fig.5 The equivalent stress of static analysis

3.2 迭代过程

结构经过优化后，可看出，变密度法过程最大密度一直在1.0，但是最小密度则由1.0 趋向于0，迭代过程如图6 所示。经过大约10 个迭代，最小密度约为0.1，然后随着迭代的深入，最小密度缓慢趋向于0。实际上，本文提供的案例在20 个迭代之后就已经可以获得较为满意的结果，在一般情况下，结果是否可以接受取决于模型的复杂程度。

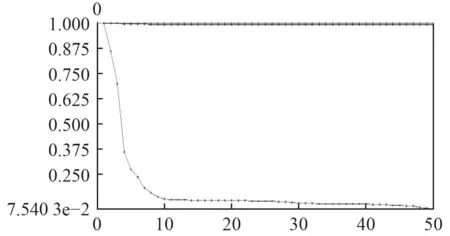
图6 优化过程曲线Fig.6 The process curve of optimization

3.3 优化结果

最终优化结果如图7 所示，可看出，绝大部分密度是1.0（图中显示0.6～1.0），在密度小于0.4 的材料单元，软件自动把它去了。根据拓扑优化结果，图中横隔板与原来面积相比减少约18%。另外，为了加工方面，两侧小块去除的部分一般仍然保留。

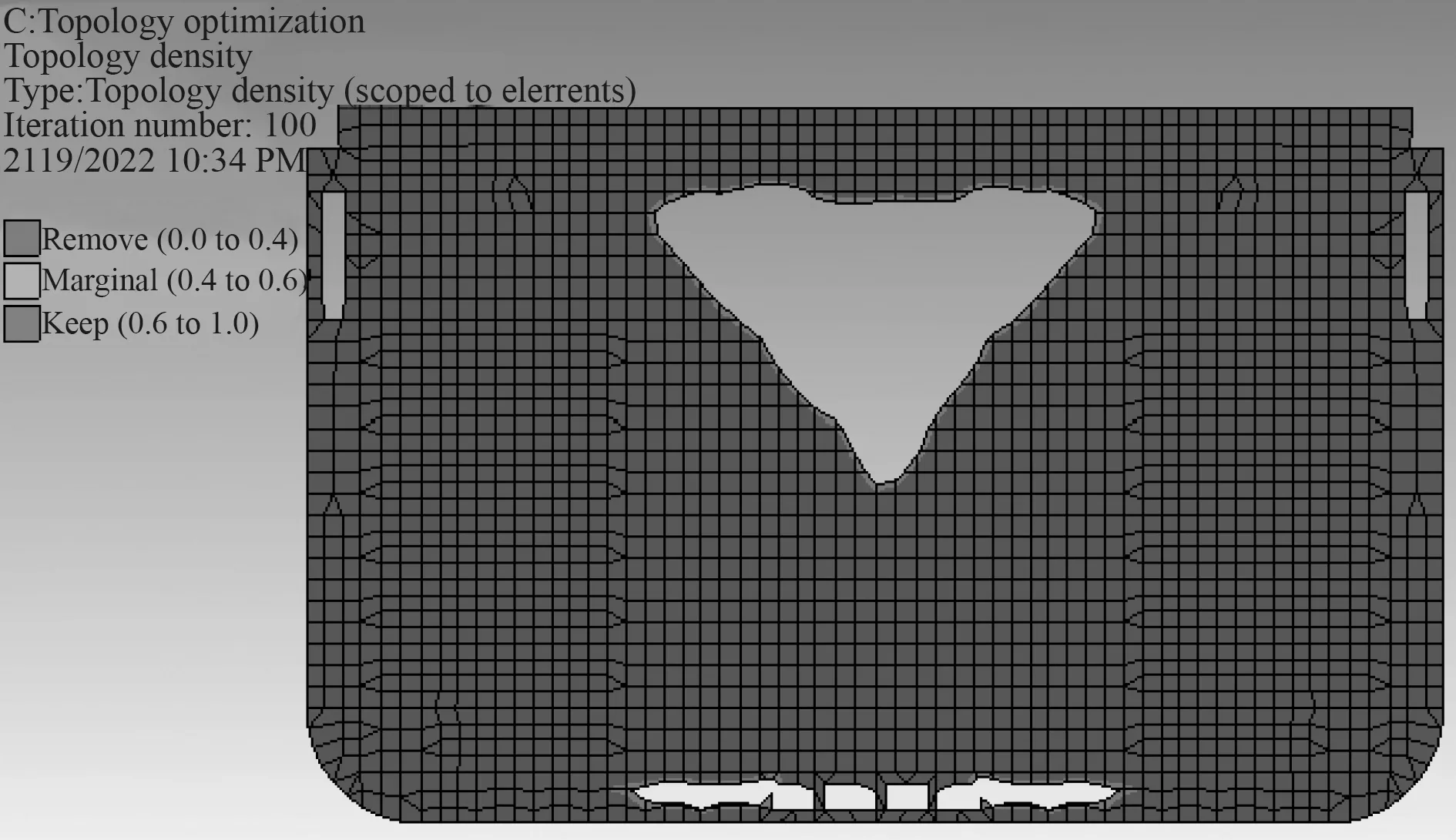
图7 优化后的形状结果Fig.7 The mesh after optimization

3.4 优化后受力结果

同样的，对优化后的构型进行静力分析。边界条件与荷载条件与优化之前相同。图8 为优化后区域的等效应力云图。由结果可知，构型最大应力为206 MPa，与优化前的应力相比较，只增加了约1.5%，优化效果非常显著。

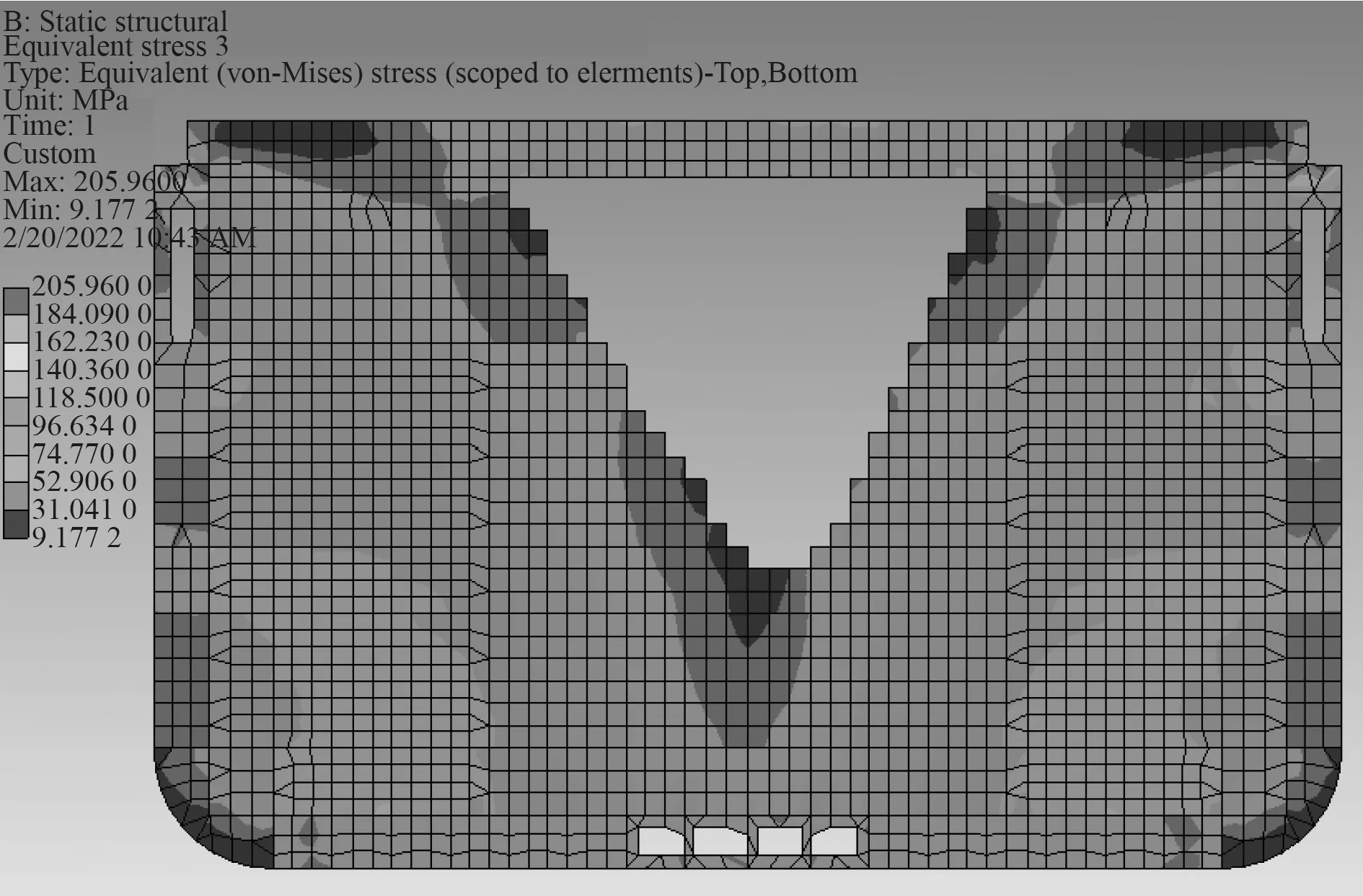
图8 优化后形状应力结果Fig.8 The stress contour after optimization

4 结 语

本文采用变密度优化算法，对某大型箱船横隔板进行了结构拓扑优化，得出最终的拓扑优化结果。研究结果表明，在指定应力强度的约束条件（最大应力不超过材料强度）以及结构质量最小的目标函数下，船舶横隔板板架拓扑结构在优化后质量可减小18%，而最大应力却只增加了1.5%。说明本文的变密度拓扑优化方法可以有效的为船舶设计提供优化依据，本文的研究结果可为类似结构件的设计提供方法借鉴。