一种基于元学习的稀疏孔径ISAR成像算法
2023-09-15夏靖远杨志雄周治兴廖淮璋张双辉付耀文
夏靖远 杨志雄 周治兴 廖淮璋 张双辉 付耀文
(国防科学技术大学 长沙 410073)
1 引言
逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)可以全天时、全天候获得远程高机动目标的高分辨率图像,已经逐渐成为获取目标观测数据的主要工具[1]。高分辨率ISAR图像对于雷达目标识别、分类和语义分割等后续任务至关重要。虽然从完整的雷达回波获取清晰的雷达图像并不困难,但是雷达系统往往受到雷达硬件和客观成像条件的限制,难以获得完整的雷达回波。稀疏孔径ISAR成像就是通过稀疏建模从不完整的回波中恢复和重建ISAR图像,在雷达目标识别、空间监视、弹道导弹防御等军用民用领域具有重要意义[2]。
现有的稀疏孔径ISAR成像算法主要分为基于模型的方法和基于深度学习的方法两大类。早年的稀疏孔径ISAR成像算法以基于模型的方法[3-12]为主,其通常根据目标ISAR图像特性(例如稀疏性),手动设计ISAR图像先验模型。具体来说,匹配追踪(Matching Pursuit,MP)[3]是经典基于模型的稀疏孔径ISAR成像方法,其利用ISAR图像具有稀疏性,通过多次迭代运算求得ISAR图像最稀疏解。正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)[4]在MP算法的基础上,在分解的每一步中对所选元素进行正交化处理,在成像精度相同的情况下提升了收敛速度。交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[5]在现有的凸优化求解框架下,利用范数正则项对待恢复信号的稀疏性进行约束,并在此基础上最小化待恢复信号与原始信号的误差。总的来说,基于模型的方法的优势在于数学模型成熟,算法的收敛性和数学可解释性较好。然而,基于模型的方法包含需要手工调整的超参数,对成像效果影响较大,且容易收敛到局部最优,不能有效地满足ISAR图像成像任务在复杂多变条件下的成像需求。
随着近年来深度学习的快速发展,基于深度学习的方法[13-23]通常设计一个端到端的深度神经网络模型,例如,深度卷积神经网络[13]、生成对抗网络[14]等。通过大量配对数据训练后,能够实现对各种图像恢复、重构任务的有效求解,但应用领域主要在于光学图像修复、超分辨、降噪等,在稀疏孔径ISAR成像方面应用较少。文献[15,16]提出了一种基于深度卷积神经网络的ISAR成像方法,通过引入深度卷积神经网络来代替基于模型方法正则化迭代求解步骤,从而实现了较好的成像性能。文献[17,18]提出了一种基于生成对抗网络ISAR成像算法,通过引入对抗损失,使得ISAR成像结果具有更好的细节纹理信息。上述方法的优点在于具有较好的数据驱动性能,但是这类方法受限于训练数据的同时,也不具备数学可解释性,不能适应条件多变的ISAR成像任务需求。文献[19]提出了基于深度展开的ADMM算法,通过深度学习的方法实现ADMM算法迭代求解中的部分步骤和超参数,使得方法具有数据驱动性能的同时,也具备较好的数学可解释性。然而这类方法仍然依赖大量的配对训练数据和预训练过程,而高质量的ISAR图像公开数据集较少且通常难以获得,训练数据集的质量对算法效果有较大影响。
在最近的非凸优化算法理论研究中,文献[24,25]提出了一种基于元学习的交替迭代最小化框架,在不需要任何训练数据和预训练过程的情况下,在传统的变量优化问题上取得了较好的收敛性能。这一优点非常契合稀疏孔径ISAR成像任务。受文献[24,25]启发,本文提出了一种基于元学习的高效、自适应稀疏孔径ISAR成像算法。所提方法通过学习辅助的交替迭代优化方式,一方面将ISAR成像问题中对ISAR图像的迭代求解转化为了对网络输入和网络参数的交替迭代更新求解,从而避免了算法对训练数据的依赖和算法的预训练需求。针对算法在求解过程中陷入局部最优这一核心问题,所提方法引入基于元学习的优化求解策略,通过考虑多次迭代步骤的累积误差来对优化策略进行实时更新,实现在全局视野中考虑到更全面的优化轨迹,从而达到算法自适应地根据收敛轨迹学习优化更新的方向和步长,从本质上确保了避开局部最优的能力。最后,基于仿真的目标ISAR图像数据设计了多组对比实验,实验结果表明:本文方法可以在没有训练数据、没有预训练的情况下进行高效自适应的稀疏孔径ISAR成像,并获得优于其他常规ISAR成像算法的性能。
2 稀疏孔径ISAR成像问题概述
本节首先介绍了稀疏孔径ISAR成像模型,然后以交替方向乘子法为例,介绍了稀疏孔径ISAR成像问题求解过程。
2.1 ISAR成像模型
一个常见的ISAR成像场景如图1所示。在目标中心建立了一个坐标系,其中,y轴沿着雷达的视线(Line-Of-Sight,LOS)方向,x轴垂直于y轴。假定雷达与被探测目标位于同一平面,则该平面构成成像平面。在实际应用中,由于雷达相干处理间隔(Coherent Processing Interval,CPI)很短,因此目标在相干处理间隔内可等效为匀速运动,目标旋转速度设为ω。所获取目标的一维高分辨距离像(High Resolution Range Profile,HRRP),表示如下:
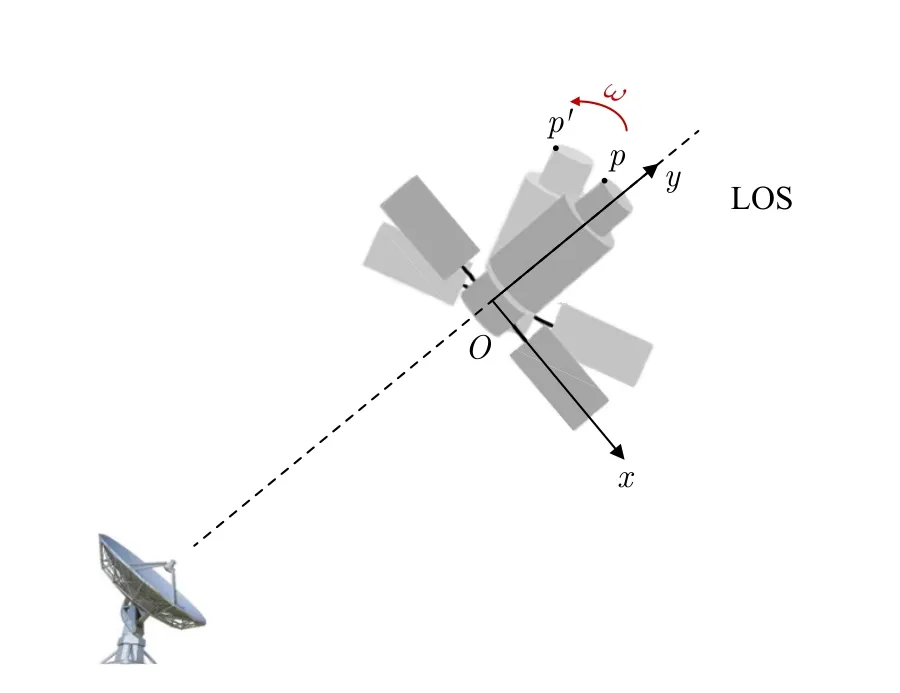
图1 ISAR雷达观测模型Fig.1 General ISAR imaging scenario
其中,τ表示快时间,t表示慢时间,fc表示中心频率,c表示光速,B表示信号带宽,σp表示散射点p的反射系数,P表示总散射点个数,rp(t)表示雷达到目标第p个散射中心的距离,rp(t)可以进一步分为平动分量rp,t(t)和 转动分量rp,r(t)两个部分:
其中,xp和yp为目标第p个散射点在图1中参考坐标系下的坐标。由于雷达CPI很短,式(2)中转动分量rp,r(t)的高阶分量可以忽略。在信号模型中,我们假设回波信号已经完成包络对齐和自聚焦等补偿操作,最终回波表达式如下所示:
此时的回波信号可通过方位向快速傅里叶变换得到目标的散射点分布。对于式(3),考虑到信号中的加性回波噪声,式(3)可写为
通过对快时间维进行快速傅里叶变换,式(4)中的回波表达式s(τ,t)可以得到ISAR一维距离像信号矩阵S,通过对慢时间维进行傅里叶变换,ISAR一维距离像信号矩阵S可以得到ISAR图像X。上述过程可进一步写成离散矩阵的形式,如下所示:
其中,S ∈CL×N表示回波一维距离像,X ∈CM×N表示二维ISAR像矩阵,A∈CL×M表示ISAR图像的退化矩阵,N ∈CL×N表示二维ISAR像的高斯白噪声矩阵。L表示稀疏回波下的方位向脉冲数,M表示原始回波下的方位向脉冲数,N表示距离像单元数。
在稀疏孔径ISAR成像场景中,观测矩阵A可建模为降采样矩阵D ∈CL×M与傅里叶变换矩阵F ∈CM×M相乘的形式A=DF。一般情况下,傅里叶变换矩阵F与降采样矩阵D是已知且确定的。降采样矩阵D的形式与稀疏模式以及稀疏率有关,其中随机稀疏模式是目前常见的一种稀疏采样模式,表示对完整的回波信号进行随机的采样、抽取。稀疏率表示降采样矩阵D中值为1的行数与总行数的比例。
在稀疏孔径ISAR成像问题中,式(5)可以被进一步改写成以下矩阵形式:
对于ISAR图像X的恢复,需要引入先验信息来构造解的约束条件,理想情况下,信号的稀疏性由l0范数约束,它表示信号的非零元素数量。但在l0范数约束下,优化问题是一个NP难问题,通常使用其他约束松弛这一问题。在压缩感知中,l1范数的优化问题是凸优化问题,为了计算方便,因此常见的做法是将l0范数用l1范数代替,此时该优化问题可以写成如下形式:
其中,β表示正则化参数。
2.2 ADMM方法
为了求解上述优化问题,通常利用ADMM方法对问题进行交替迭代求解。该算法首先引入隐变量H,将无约束优化问题式(7)转化为以下约束优化问题的形式:
根据式(8)可进一步写出其增广拉格朗日函数:
其中,ρ表示惩罚系数,α∈CM×N表示拉格朗日乘子,αH表示矩阵α的共轭转置。ADMM算法将问题拆解成两个子问题,并通过交替迭代最小化的方式对其进行分别优化,最终可以得到如下迭代过程:
其中,上标 (k)表示迭代次数。对于式(10)中前两个迭代过程,令Lρ(X,H,α)对X与H的偏导数分别为0可得到相应变量值的闭式解,式(10)中第3个迭代可直接计算得到,α与ρ为超参数,实际应用时通常根据问题和应用场景进行设定。
3 所提基于元学习的稀疏孔径ISAR成像算法
本文方法主要由基于学习辅助的交替迭代求解和元学习优化两部分组成,本节首先介绍基于学习辅助的交替迭代优化模块。然后在此模块的基础上,介绍所引入元学习优化策略。最后介绍本文算法的总体实现流程以及计算复杂度分析。
3.1 基于学习辅助的交替迭代优化
稀疏孔径ISAR成像问题的矩阵形式如下所示:
其中,第1项为数据保真项,第2项为先验项。令k为迭代次数,在第k次迭代中,本文方法并不像传统算法一样直接求解ISAR像X(k),而是通过引入一个复数神经网络GX作为ISAR像生成网络辅助求解式(11)。其中,ISAR像X(k)由一个复数神经网络GX生成,网络GX的输入为一个高斯噪声ZX ∈CM×N,噪声ZX ∈CM×N随算法的更新迭代过程而更新,ISAR像X(k)的生成过程如下所示:
对于式(13)这种多变量优化求解问题,通常采用交替迭代最小化算法进行求解,表示如下:
3.2 元学习优化
由于式(11)的病态性,直接通过式(16)和式(18)穷尽地对网络输入ZX和 网络参数θX进行交替迭代求解仍然容易陷入局部最优解。本文提出一种基于元学习交替迭代求解策略,利用一段累积的损失LθX作为元学习损失Lmeta并用于更新网络参数θX,元学习损失的计算表示如下:
其中,k表示网络元学习更新的迭代次数,T表示一次元学习损失计算利用的损失LθX数量。通过Adam优化器优化更新网络参数θX,表示如下:
值得注意的是,传统元学习往往需要少量训练数据作为样本来训练网络模型,网络模型在多个不同任务下进行训练,使得模型具备更好泛化性能。本文所提的元学习方法与传统元学习方法不同的是:本文所提的元学习方法将算法的一次迭代过程视为元学习的训练样本,通过跨多个不同的迭代过程的元学习损失Lmeta对网络参数进行更新,使得算法具有更好全局更新视野。在这种情况下,网络参数不再最小化每个单独的图像重建损失LθX,而是通过最小化累积的元学习损失Lmeta来优化网络参数,因此实现了一种非贪婪且自适应的优化策略。更多的元学习优化细节可以参考文献[24,25]。
3.3 整体实现
本文方法的总体实现流程如算法1所示。其中,网络GX的结构示意图如图2所示,网络GX为一个8层的全卷积神经网络,从输入到输出的卷积通道数分别为1,16,32,64,128,64,32,16,1,卷积核大小均设置为N=3×3,图2中绿色箭头、红色箭头、蓝色箭头和黑色箭头分别表示卷积层、池化层、转置卷积层和跳跃连接。网络GX的所有网络参数在随机初始化后,通过本文所提的元学习策略进行优化。值得注意的是,利用式(15)和式(17)计算得到的损失更新网络输入与网络参数时,网络输入ZX和网络参数θX是没有经过任何预训练的,也不需要任何的训练数据。在实际应用中,网络输入ZX和 网络参数θX从一个完全随机初始化的开始,将每一次迭代过程视为一个训练样本,随着问题式(14)的迭代求解而更新,即实现了一种“即插即用”的在线求解模式。

算法 1 一种基于元学习的稀疏孔径ISAR成像算法Alg.1 A meta-learning based sparse aperture ISAR imaging method

图2 本文方法网络结构示意图Fig.2 The network architecture of the proposed method
综上所述,本文所提出的基于元学习的稀疏孔径ISAR成像算法在求解过程中,通过式(12),将对变量求解的优化问题转化成了对网络输入和网络参数求解的优化问题。通过式(14)将原问题分解成了两个子问题,并进行交替迭代求解,实现了一种“即插即用”的在线求解模式,避免了方法对训练数据的依赖性。而元学习的优化迭代策略则通过式(19)和式(20)计算迭代过程中累积的元学习损失,并用于更新网络参数,最终实现了一种自适应、非贪婪的优化策略,保证了算法的稀疏孔径ISAR成像性能。
3.4 计算复杂度分析
4 实验结果与分析
4.1 实验设置
本文所用测试数据集是一个仿真的空间目标ISAR图像数据集和一个实测数据集。其中仿真数据集共有3000张空间目标ISAR图像,包含3个不同角度的3种不同空间目标。实测数据集包含类别为Yak42的飞机目标。其中每张空间目标ISAR图像的大小为240×240。在测试阶段,本文方法不使用任何数据进行训练,也没有任何的预训练过程,在求解过程中仅仅已知ISAR一维距离像S。考虑到空间目标ISAR图像通常是灰度图像,图像的可视化效果较差。为了达到增强ISAR图像可视化效果的目的,我们通过伪彩色渲染增强灰度ISAR图像,以获得更好的可视化效果。在对比实验中,本文方法将对比基于模型的ISAR成像方法:距离-多普勒(Range-Doppler,RD)算法、正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[4]和ADMM算法[5],以及基于学习的ISAR成像方法:基于复数展开网络的ADMM (Complexed-Unfolding ADMM,CU-ADMM)算法[19]。ISAR图像质量评价指标采用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)、均方根误差(Root Mean Squared Error,RMSE)和图像熵3个数据指标。
4.2 实验结果及分析
表1给出了在稀疏率为0.25的情况下,5种不同ISAR成像方法在仿真数据上得到的图像熵、PSNR值和RMSE值。在表中我们能够发现本文方法在所有条件下都实现了最好的ISAR成像性能。尤其是在PSNR指标上,本文方法高出性能第2名算法0.79 dB。表2进一步给出了稀疏率在0.125条件下,不同方法的对比结果。我们可以看到本文方法仍然实现了最好的性能。图3进一步展示了所有ISAR成像方法在两种稀疏率条件下的可视化结果对比。我们可以看到本文方法的ISAR成像结果在定性的视觉效果上均更接近真值ISAR图像。

表1 不同方法在仿真ISAR数据集上的平均成像性能对比(稀疏率为0.250)Tab.1 The average imaging results on the of the simulated ISAR data (sparsity rate 0.250)

表2 不同方法在仿真ISAR数据集上的平均成像性能对比(稀疏率为0.125)Tab.2 The average imaging results on the of the simulated ISAR data (sparsity rate 0.125)

图3 不同ISAR成像方法在仿真数据上的可视化对比结果Fig.3 The visual imaging results on the of the simulated ISAR data
表3和表4分别给出了稀疏率为0.250和0.125的情况下,5种ISAR成像方法在实测数据上得到的图像熵、PSNR值和RMSE值。在表中我们能够发现本文方法在所有条件下都实现了最好的ISAR成像性能。尤其是在稀疏率更低的条件下(稀疏率为0.125),本文所提方法在PSNR指标上高出性能第2名算法0.51 dB。图4和图5进一步展示了所有ISAR成像方法在实测数据上两种稀疏率(0.250和0.125)条件下的可视化结果对比。可以看到本文方法的ISAR成像结果在定性的视觉效果上均更接近真值ISAR图像。

表3 不同方法在实测ISAR数据集上的平均成像性能对比(稀疏率为0.250)Tab.3 The average imaging results on the of the real ISAR data (sparsity rate 0.250)

表4 不同方法在实测ISAR数据集上的平均成像性能对比(稀疏率为0.125)Tab.4 The average imaging results on the of the real ISAR data (sparsity rate 0.125)

图4 不同ISAR成像方法在实测数据上的可视化对比结果(稀疏率为0.25)Fig.4 The visual imaging results on the of the real ISAR data (sparsity rate 0.25)

图5 不同ISAR成像方法在实测数据上的可视化对比结果(稀疏率为0.125)Fig.5 The visual imaging results on the of the real ISAR data (sparsity rate 0.125)
4.3 消融实验
表5和图6分别给出了本文方法中所引入的元学习优化策略在仿真数据上的消融实验结果。其中“无元学习模块”表示本文方法不采用元学习的求解策略,当T设置为1时,也就是当元学习仅累积1次梯度信息时,本文所提的元学习方法退化为经典的交替迭代最小化方法。在表5中我们能够发现本文方法在所有条件下都实现了最好的ISAR成像性能。本文方法在没有引入元学习模块的情况下,出现了1 dB左右的PSNR值性能下降,而图像熵和RMSE评价指标也有一定程度的性能下降。因此,该消融实验验证了本文方法中元学习优化策略的有效性。
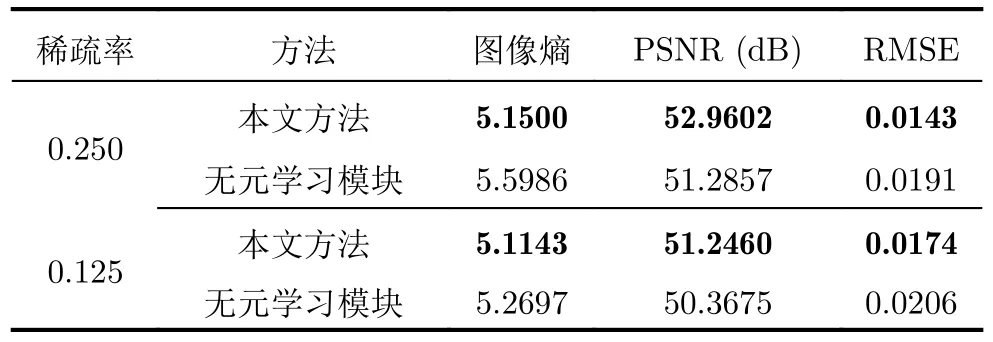
表5 本文方法中元学习优化的消融实验Tab.5 The ablation studies of the proposed method
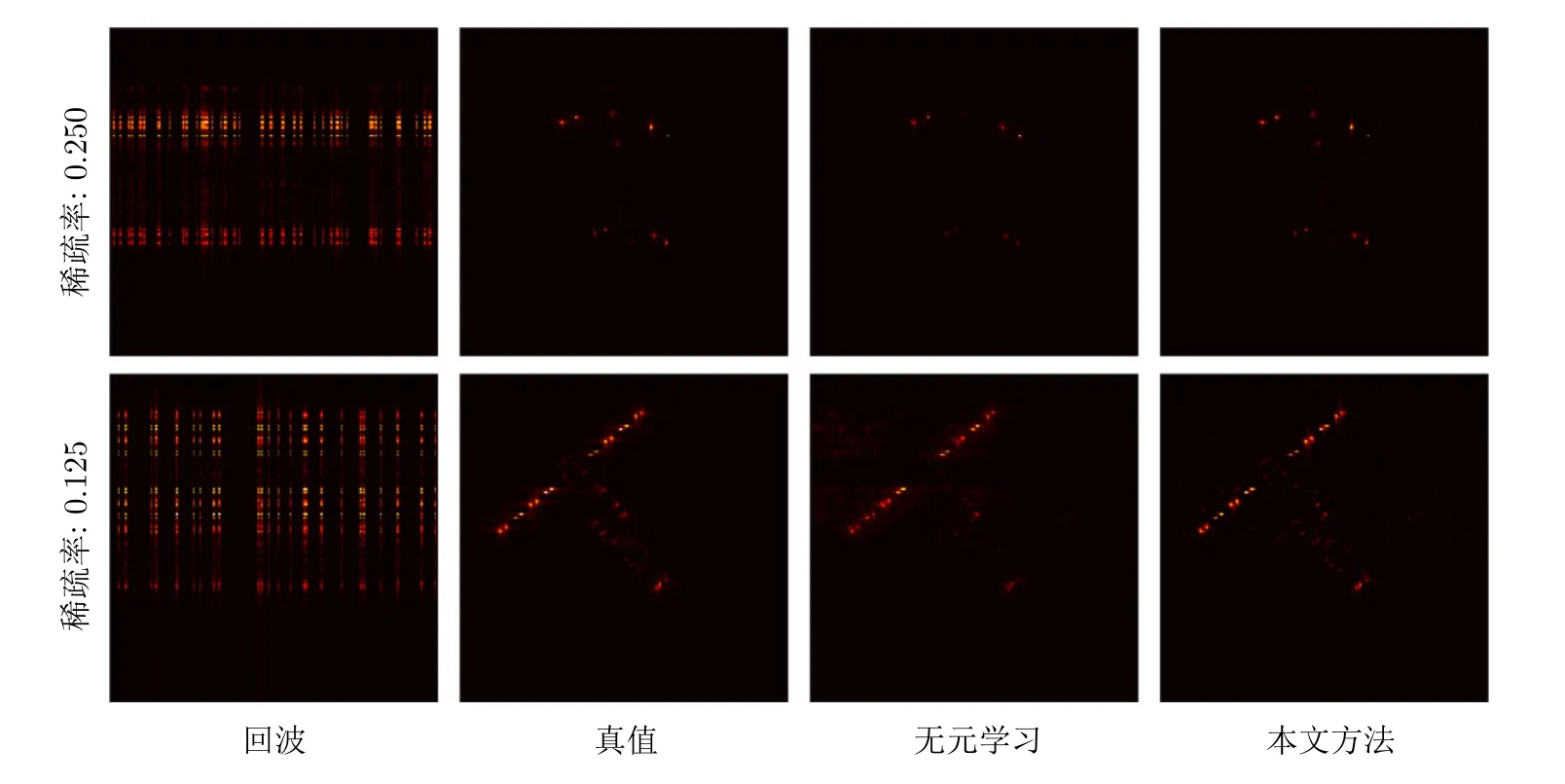
图6 消融实验成像结果Fig.6 The visual results of the ablation studies of the proposed method
4.4 计算复杂度
表6给出了5种不同ISAR成像方法的计算复杂度对比,其中计算机CPU为Intel Core i7-11800H,显卡配置为GeForce RTX 3090 GPU。从表6中可以发现本文方法的测试时间较大。这是因为元学习优化迭代策略的引入,本文方法在测试的迭代过程中需要反复对网络参数进行更新。但是本文方法的计算复杂度是较低的,仅与ISAR图像大小M的2次方成正比,且没有训练时间消耗。综合考虑算法的计算复杂度、训练时间以及测试时间,本文方法具有适中的计算成本。
5 结语
本文提出了一种基于元学习的高效、自适应稀疏孔径ISAR成像算法。所提方法通过学习辅助的交替迭代优化方式,避免了方法对训练数据的依赖;本文方法通过基于元学习的优化求解策略,从本质上确保了避开局部最优的能力。最后,本文方法在含有多种不同的ISAR仿真、实测数据集上进行了广泛的对比实验并在图像熵、PSNR值和RMSE值3个评价指标上均实现了更好的ISAR成像性能。但本文方法的运算效率还有进一步提高的空间,且并没有考虑到的ISAR成像过程中的运动补偿。后续我们将针对ISAR运动补偿与稀疏孔径成像一体化问题开展研究。
