基于太赫兹雷达的声致海面微动信号检测
2023-09-15王宏强
邓 彬 李 韬 汤 斌 易 俊 王宏强 杨 琪
(国防科技大学电子科学学院 长沙 410073)
1 引言
当水下声源发射声波传播至水-空界面时,由于空气和水的声阻抗差距较大,水面会被声信号激发而产生表面波动,称之为声致水面[1]。研究表明,水下声源所激起的水面微幅波振动频率与水下声源振动频率相一致[2]。利用这一特性,可以通过测量水面振动信号反演水下声源信息,实现水-空跨介质通信和水下声源探测。
根据不同介质特性,在空中和水中的信号传输方法已经较为成熟。在空中,信号能够依托电磁波通过交变的电场和磁场互相激发进行空间传播,目前已经被广泛应用于各个领域[3]。水中信息传输主要依靠声波,声波是一种机械波,可以在水中传播较远距离,采用水声通信方式可实现水下节点的双向通信[4]。但是由于衰减和水-空边界阻抗特性差异限制,微波及声光均无法实现跨介质传输。对于电磁波,海水的介电常数高,导致电磁波难以穿透水层,严重阻碍了信息数据链的水下延伸[5];对于声波,其振动难以透过水-空这一弹性边界层向外传播;而蓝绿激光水下衰减相对较小,但依赖于海水可见度且传输距离一般限于百米以内。综合来看,目前尚无有效的水-空跨介质通信方法和手段。但是,随着人类对海洋探索的不断深入和水下攻防对抗的日趋激烈,水-空跨介质信息传输需求越来越强烈,已经成为制约水下航行器战斗力提升的一大关键问题[6]。因此,迫切需要发展新的水-空跨介质通信技术,同时支撑涉水光学等学科方向发展。通过检测声致水面振动信号反演水下声源传递的信息,为实现水-空跨介质通信提供了一种有效途径。
水下航行器探测以声学探测为主,固定水听器阵列只能监测固定水域,需要时间建设,成本较高;拖曳声呐受平台的限制,移动速度慢且易受自噪声影响,探测需要一定时间投放展开;投放式声呐只能定点探测,投放后工作时间有限,使用后需要回收,有设备损失风险。近年来,为了满足不断提高的水下感知需求,非声探测技术蓬勃发展[7],以水下航行器非声物理场探测及其运动引起的尾流探测为主,常用的方法有磁探测、激光探测、红外探测、水动力尾迹遥感探测等,多处于研发验证阶段。目前较为成熟的以航空磁探测为主,其磁异信号强度随距离呈三次方衰减,因此难以提升探测距离,传感器感应范围通常在1 km内,且易受海底沉船矿藏等金属及地磁场的影响。水下航行器在航行或作业时,其推进器和各种机械都在工作,其产生的振动通过船体向水中辐射声波[8],具有声源种类多、分布相对集中、噪声强度大、频谱复杂等特性。水下航行器在近水面航行或高速航行产生较大辐射噪声时,其辐射噪声传导至水面激励起水面振动,其信号也包含了水下航行器噪声的相关信息。因此基于小型无人机载平台探测水下航行器辐射噪声激励的水面振动,具有机动性好、成本低、部署灵活等特点。作为现有探测手段的补充,能够为水下航行器的探测乃至识别提供重要依据。
目前,国内外关于声致水面振动信号检测的手段主要利用激光和微波。在激光探测声致水面方面,美国杜兰大学的Lee等人[9]最早用激光设备进行了声致水面探测,建立了声致水面简单的理论模型,根据水面反射光强受水面振动影响的原理,推导了接收光强与水下声源频率的关系,并进行了实验验证。国内也在激光探测声致水面振动方面取得了一系列成果。2003年,哈尔滨工业大学宫彦军等人[10]利用声致水面调制并散射后的散射光提取到了水下声信号,并在实验中探测到了300 Hz以下的水下低频声信号。但是,该方法是间接测量散射屏上的光强来探测声致水面振动,由于散射后的光信号非常微弱,所以该技术在实际应用中存在较大局限性。激光设备可实现高精度位移测量,但是激光设备的固有缺陷限制了其实际应用:激光设备在体积、寿命、效率等方面存在较大缺陷,难以适应星载和机载需求;更为重要的是,激光光斑一般较小,难以实现目标稳定跟踪和探测,实用性不强[11-13]。在微波雷达探测方面,2018年,美国麻省理工学院Tonolini等人[14]基于中心频率为60 GHz、带宽3 GHz的毫米波雷达,展开了跨介质水声-雷达通信(Translational Acoustic-RF communication,TARF)的原理性验证。验证试验在水池环境中展开,水声喇叭在水下最深3.6 m处发射100~200 Hz的声信号,利用毫米波雷达系统对水面振动实现了探测,为微波雷达水-空跨介质信息传输提供了新的思路,但是受频段和带宽的限制,探测精度和杂波适应能力有限。
太赫兹(Terahertz,THz)波处于微波毫米波和红外光学之间的过渡频段[15],由于波长短、频段宽,能够获取目标极为精细的结构、运动和材料特性,具有极高的时、空、频分辨力,在军事和民用等领域已经展现出广阔的应用前景。随着近年来太赫兹雷达的快速发展,太赫兹频段的大带宽、高分辨、多普勒敏感性等优势逐渐凸显,尤其是在微小运动参数提取和估计方面其优势显著[16],可在声致水面探测和提取方面发挥重大作用。因此太赫兹雷达兼顾了激光设备和微波雷达的优势,不仅探测精度高,而且稳定性好,基于太赫兹雷达的声致水面微动信号检测技术对实现水-空跨介质信息传输有重要意义。
本文首先分析了声致水面的理论模型;然后研究声致水面微动信号检测方法,结合信号特点,提出小波-卡尔曼滤波方法以滤除干扰和噪声信号,首次在二级海况下利用真实外海数据对所提方法进行验证并成功实现强海杂波中亚微米尺度微动信号的精细化提取;最后进行归纳总结。
2 声致水面微动建模
2.1 水下声传播模型
水声信号在传播中伴随着衰减,主要为扩展损失、吸收损失和散射[8]3个方面。扩展损失通常指传播过程中随波阵面的扩展引起的声强衰减,与声源的声场几何辐射场有关;吸收损失指通过介质带来的物理衰减;散射主要指介质本身的不均匀和杂质及海水边界等造成的散射衰减。本文研究内容及实验在浅水低频声场环境中开展,不考虑散射影响,主要考虑声源正向辐射至水-空界面的声强变化,采用射线理论对声传播路径上的损失进行简要分析。通常定义传播损失:
其中,I(1),I(r)分别是离声源等效声中心1 m和r处的声强。根据以上叙述可知,传播损失TL应由扩展损失和吸收损失两部分组成,即传播损失TL=扩展损失TL1+吸收损失TL2。对于扩展损失,通常定义为
其中,n为常数,因传播条件而改变。声信号在水下传播形式可以分为球面波、柱面波、平面波等。距离声源很远时,可按远场平面波进行分析,n取0。处于近场时,对于点声源,在理想情况下考虑球面辐射,此时n取2。对于吸收损失,定义为
其中,α为海水中的声衰减系数。水中声传播衰减可依据经典衰减理论进行分析,当频率较低时,吸收系数按经验公式[17]与声波频率、深度的变化关系:
其中,f为声源频率,α单位为dB/km,h为水深,单位为m。不难看出,衰减系数随声源频率增加而增大,随水深度增加而减小,对于本文中近水面模型其衰减远小于1 dB,因此在计算时可以忽略,故在本实验中只需考虑扩展损失TL1。
2.2 水面振动模型
声致水面振动探测理论推导过程已有详细证明[18],下面引用其结论进行分析。Pi为传播到介质交界面的点声压级。平行于静止水面的坐标轴为x轴,垂直于静止水面的坐标轴为y轴,可以推导出声致水面波动随时间t变化的数学模型为
其中,ω为声波的角频率,ρ为水的密度,c为声波在水介质中的传播速度,k为水面波动的波数,α′为声致水面波动振幅衰减系数,其与式(4)中描述的声传播衰减系数α不同,可表示为
其中,µ为水介质黏度,g为重力加速度,σ′为表面张力系数。当位于点声源正上方时,即x=0时,得到引起最大振幅ymax:
根据式(7)可知,声致水面波动的幅度是与声波的角频率ω成反比的,即水下声波信号的频率越高,在水面上产生的振动幅度越小,且振幅从声源中心位置向四周逐渐衰减。图1展示了位于水下1 m、声源级为180 dB的点声源,引发的水面振幅最大值和传播衰减系数在频率50~1000 Hz处的变化趋势。可以看到随频率增大水面波动振幅衰减系数不断增大,引起的水面振幅急剧减小。在该条件下,水面振幅在低频段为数微米,当频率进一步升高时,降至纳米量级。该结论已通过激光干涉测量[19]得以验证。而实际中只有在远场条件下声源才能够等效于质点。近场时,声致水面为声源振动单元和辐射声场耦合的振动区域,其形制更为复杂,难以通过数值解定量描述,但由振动的传播特性可知,此时水面振动可视为多个同频振动声源的耦合,其水面振动频率仍为声源频率。而推导得到的点声源振幅能够对近场条件下水面振幅提供参考。
图2展示了位于水下1 m、声源级为180 dB、频率为50 Hz的声源引起的振幅。当声波频率更高时,其产生的水面振幅更为微小,用传统的微波雷达将无法精确探测,而太赫兹雷达可充分发挥高精度的优势。

图2 声致水面振动俯视及纵向剖面振幅示意图Fig.2 Schematic diagram of top view and longitudinal profile amplitude of acoustic water surface vibration
3 声致水面微动信号建模与信号检测
3.1 雷达回波信号模型
由于水下声源引起的水面振动幅度较小,传统的雷达测距方法无法探测如此微弱的振动信号。雷达探测目标时,目标到雷达的距离变化会引起回波相位相应的变化。通过对回波相位的分析,反演出目标到雷达的距离,称为相位测距[20]。相位测距的精度较高,能够很好地提取出目标的微动信号。下面具体介绍雷达发射线性调频(Linear Frequency Modulation,LFM)信号检测声致水面微动信号的过程。
雷达发射LFM信号的形式为
式(11)3个相位项中,第1项为多普勒项,第2项为剩余视频相位,第3项为回波包络斜置项。提取目标所在距离单元的相位,即提取fi=-2γ/c时相位。当R∆较小时,第2项和第3项可以忽略,则所提取相位为4 πfc/cR∆,通过相位的变化可以反演出目标到参考的距离变化。从宏观上分析,理解起来更加直观。电磁波在传播过程中,每传播一个波长λ的距离,相位变化为2 π。对于雷达回波,目标位置变化一个波长λ的距离,电磁波需要传播2λ距离,相位变化为4 π,根据该关系可得
从式(13)可以看出,相同的距离变化,雷达频段越高,引起的相位变化越大。因此太赫兹雷达在测量目标微动方面具有天然的优势。
相位测距的精度越高,在能够更好地提取出目标的微动信号的同时,也会更容易出现相位缠绕现象。目标距离单元提出的相位一般被限制在-π到π 之间,当R∆引起的相位变化超出这一范围时,真实相位变化会被加上或减去 2π的整数倍,从而落在这一范围内,即出现了相位缠绕现象。这时,提取的相位不能直接反映距离的变化,需要进行相位解缠。本文采用通过相邻采样点相位的比较,来进行相位解缠。
3.2 信号滤波与提取
实际中,水面振动容易受到外界环境的影响,而且即便水面处于平静状态,没有外界的干扰,其表面也会存在微小的自然波动。雷达相位测距提取的水面位移包含了声源引起的水面振动、水面自然波动或外界环境的干扰、雷达的相位噪声,其中水下声源引起的振动信号比较微弱,而干扰信号和噪声信号幅度相对较大。在强干扰强噪声的背景下,提取声源引起的水面振动信号目前还没有很好的算法。结合水面振动信号的特点,本文提出了适用于声致水面雷达探测信号的小波-卡尔曼滤波算法,算法流程图如图3所示。小波阈值法可以处理非平稳信号,通过小波阈值法可以提取出水面的自然波动和外界的干扰信号。原始信号去除干扰信号后,再通过加窗形成短时的平稳信号,利用卡尔曼滤波去除雷达的相位噪声,最终提取出由水下声源引起的水面振动。
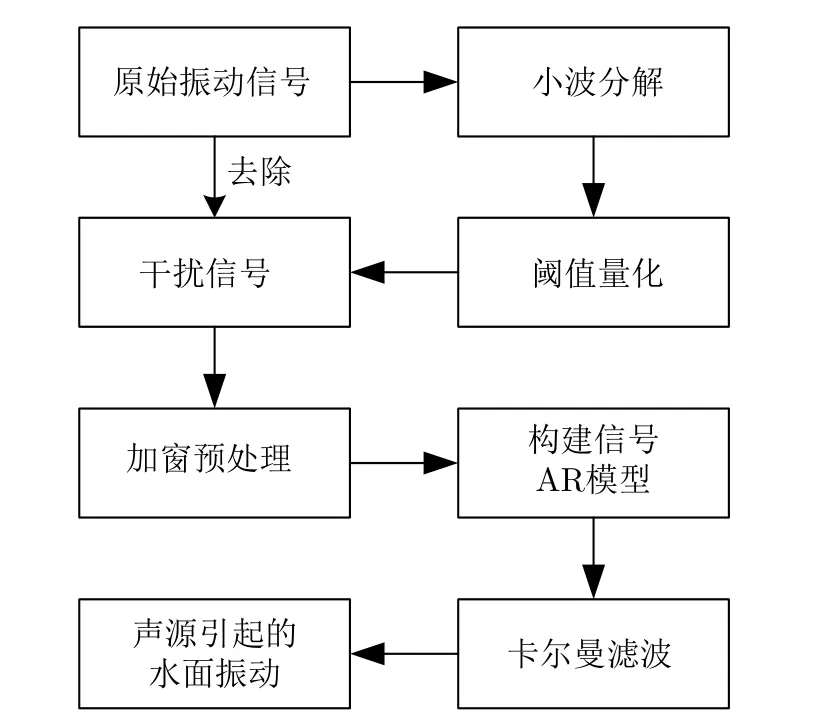
图3 小波-卡尔曼滤波算法流程图Fig.3 Flowchart of wavelet-Kalman filtering algorithm
原始振动信号首先经过小波分解,选取合适阈值量化小波分解系数,依据量化后的小波系数,重建低频信号。小波阈值法提取出的信号分量是水面自然波动或外界干扰的低频干扰信号,原始的振动信号减去提取出的干扰信号,就得到水下声源引起的水面振动和雷达带来的相位噪声。雷达的相位噪声属于加性噪声,与水下声源引起的水面振动不相关。水面振动信号具有短时平稳特性,对信号进行加窗预处理后,每一个窗内的数据都可近似为平稳信号,符合卡尔曼滤波算法的要求。根据卡尔曼滤波算法的步骤,建立信号的自回归(Auto-Regressive,AR)模型,通过线性预测分析(Linear Prediction Coefficient,LPC)估计方法求得线性预测系数,代入到卡尔曼滤波算法的方程中,最终得到滤波后的信号。
3.3 声致海面微动信号检测分析
对于期望应用的海面场景,当前未有相关实验和结论。雷达探测海面微动信号需要面临海面噪声大及信号检测困难等问题,下面进行简要分析:
(1) 由于海面液面倾斜变化导致接收回波强弱变化,且当倾角过大时由于液面主体的镜面反射作用,使反射回波超出了接收机的灵敏度,或是超出了天线接收范围,导致接收信号中断;
(2) 液面的起伏使雷达检测到的等效相位中心位置在不断变化,等价于跟踪液面的位置在不断变化;
(3) 液面位置随波浪起伏不断跨越雷达探测的距离门,而相位的变化在不同距离门间不能统一计算,影响了信号采集的连续性和有效性;
(4) 通过相位测量液面微动,在对微动测量的同时也是对液面起伏的采样,因此对采样信号进行分析时也包含液面起伏变化,且起伏信号的强度远大于微动信号的强度,即原始振动信号中包含大量低频信号;
(5) 海浪中的气泡和破碎浪会给反射信号带来噪声,海风吹起的毛细波可能掩盖声致水面的细微纹波。
综上,在海面波浪起伏较大的情况下,采集的振动信号包含大量噪声,降低了信号强度,使信号不连续,因此需要研究雷达体制,同时使用合适的算法,才能够准确识别提取信号。从雷达体制上看,需要有更高的距离分辨和脉冲重复频率,当海浪波动引起的回波距离单元变化时,在变化中同一个距离单元内能够采到更多的信号,采集信号更连续,才能够更有效分离提取信号。
相比传统微波雷达,太赫兹雷达在声致水面微动的测量及应用上具有较大优势,能够一定程度上降低上述问题带来的影响,为后续降噪算法提供更好的数据源,具体表现在:
(1) 波长更短。太赫兹频段对目标微动更敏感,从式(13)可以看出,波长短其对相位能反映更微弱的振动幅值变化,对微米级的水面振动探测能力更强,对附着在海浪中的声致水面纹波有更好地检测提取能力,而微波雷达相位及多普勒敏感性较低,微小位移检测能力和测距精度较低;
(2) 波束更窄。将海面回波视为多散射中心集合,窄波束下照射的海面区域近似一块光斑,从波程上看,其回波对应的液面起伏程度更小,故其各散射点回波的波程相近,对应距离单元相位信息的能量更加集中;从波束范围上看,窄波束能够有效避免照射范围内存在多个海浪峰,减少散射点数量,更好地追踪液面减少周围海浪噪声。微波雷达相同孔径下波束更宽,对应照射海面起伏更大,其距离单元的相位信息包含更多不同波程的散射中心,能量更为分散,同时照射海面范围更大,相较而言引入了更多的水面杂波及环境噪声;
(3) 带宽更大。太赫兹雷达具有更大带宽,其时宽带宽积更大,雷达回波增益更高,能够获得更好的信噪比和更高的距离分辨率;
(4) 散射更强。海面对太赫兹频段电磁波散射更强,同功率下雷达能接收信号更强。
4 声致水面微动信号提取方法验证
实验采用的雷达参数设置如表1所示,实验中设置了两组雷达作为对比,以验证太赫兹雷达的探测优势,其中采样频率是快时间的采样频率。

表1 雷达实验参数设置Tab.1 Radar experiment parameter setting
4.1 水池实验验证
雷达探测声致水面微动的大型综合消声水池实验场景如图4所示。实验所用水池长20 m、宽8 m、深7 m,水池6个面都覆盖有圆锥型橡胶尖劈板,用来吸收入射声波,减少界面反射,形成自由声场环境。水池上有两个可移动的活动平台可供开展雷达探测水面实验。雷达垂直照射水面,距离水面0.6 m。声源选用水下扬声器UW30,频响范围100 Hz~10 kHz,具有良好的低频响应,在水下具有全向覆盖范围,实验使用监听器进行标定后,所发射信号声源级为160 dB。对应于本文中,水深较浅且频率相对较低,换算得此项传播衰减在1 dB以下,故忽略水下声场传播声损失,考虑声源特性依据半球面波声压变化规律。

图4 水池实验场景Fig.4 Pool experiment scene
声源通过尼龙绳吊在水中,到水面的位置精确可调,实验过程中一直保持最大输出功率不变。标准水听器用于水下发送声信号的标定,确定水下实际的发送参数信息,保证实验全过程中声信号声压平稳。
4.1.1 发射声源信号形式
声源发射信号分为以下3种形式:
(1) 连续间断发射单频信号,从50 Hz开始,以50 Hz为间隔,持续到500 Hz,再以100 Hz为间隔,持续到2 kHz。每个频点信号持续2 s,间隔时间2 s。信号形式如图5(a)所示。
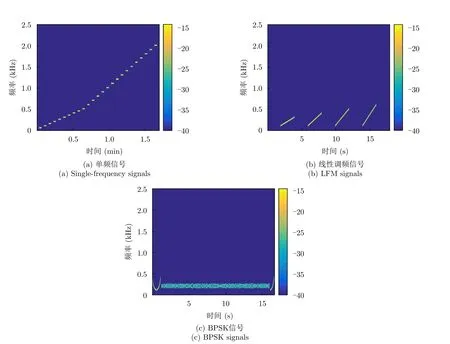
图5 发射信号示意图Fig.5 Schematic diagram of the emitted signal
(2) 共发射4组线性调频信号,信号持续时间为2 s,间隔时间2 s,开始频率为100 Hz,带宽分别为200 Hz,300 Hz,400 Hz,500 Hz,信号形式如图5(b)所示。
(3) 以二进制相移键控(Binary Phase Shift Keying,BPSK)调制方式调制的通信信号,载频200 Hz,带宽200 Hz,通信速率为100 bit/s,信号形式如图5(c)所示。
4.1.2 平静水面情况下的实验结果
声源位于水下0.2 m处,平静水面状态下,声源发射信号为单频信号时,太赫兹雷达回波数据处理过程如图6所示。

图6 122.5 GHz太赫兹雷达水下0.2 m声源无干扰单频信号处理结果Fig.6 122.5 GHz Terahertz radar underwater 0.2 m sound source without interference single-frequency signal processing results
作为对比,将太赫兹雷达和中心频率为24.5 GHz的微波雷达在相同实验条件下进行声致水面探测,经过相同的算法处理,实验结果如图7所示。
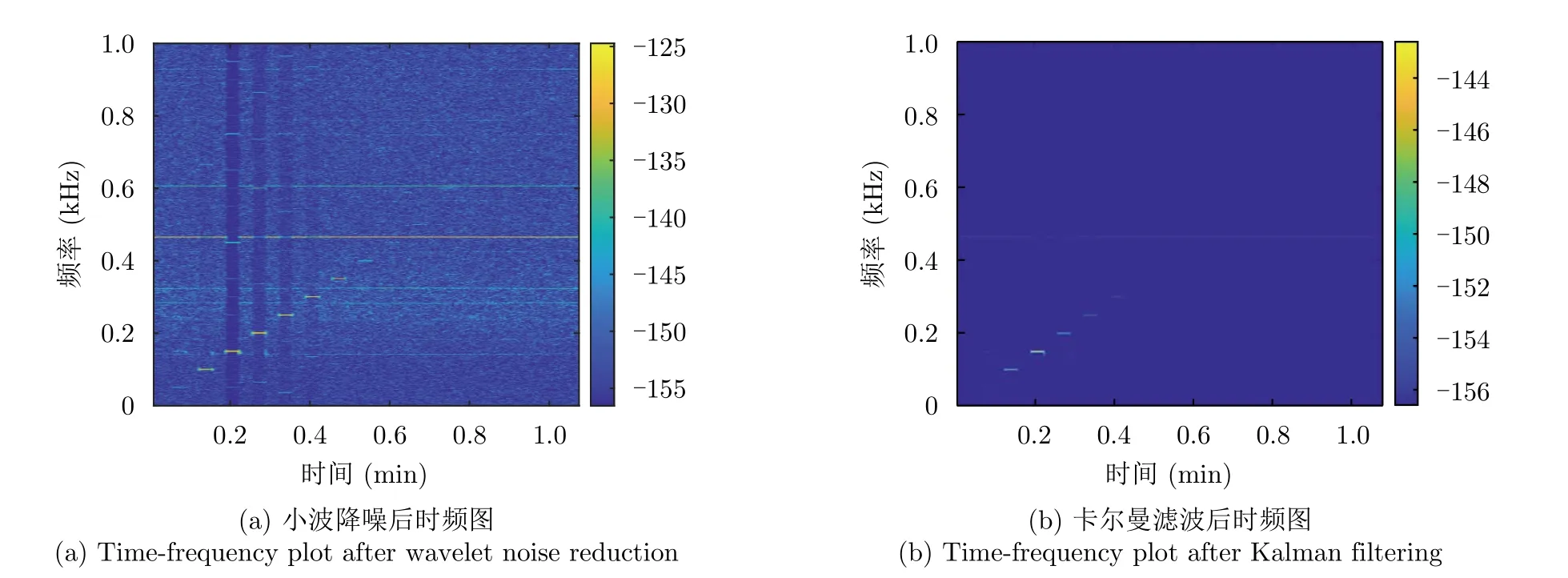
图7 微波雷达水下0.2 m声源无干扰单频信号处理结果Fig.7 Microwave radar underwater 0.2 m sound source without interference single-frequency signal processing results
从两部雷达的卡尔曼滤波后图6(d)与图6(b)看,太赫兹122.5 GHz雷达经卡尔曼滤波后能准确探测最高500 Hz的信号,提取到了9条信号谱线;微波雷达经卡尔曼滤波后能准确探测最高300 Hz的信号,提取到了5条信号谱线。对比两部雷达的处理结果可知,在相同算法处理下,微波雷达噪声明显大于太赫兹雷达,因此后文主要利用太赫兹雷达进行研究和验证。
在太赫兹雷达测量结果中,对比图6(c)与图6(d),在卡尔曼滤波处理中,检测到的部分高频信号太弱随噪声被滤除。为获得系统最大可探测频率并解算出相应振幅,将接收信号小波降噪后局部放大后如图8(a)。从图上观察最大探测到1100 Hz信号。为验证观测准确性,截取处理后包含250~1500 Hz信号的数据,使用周期图法进行功率谱估计,结果如图8(b)所示,可知最高频率探测到1100 Hz的信号。同样方法对应于微波雷达,其探测频率为400 Hz。
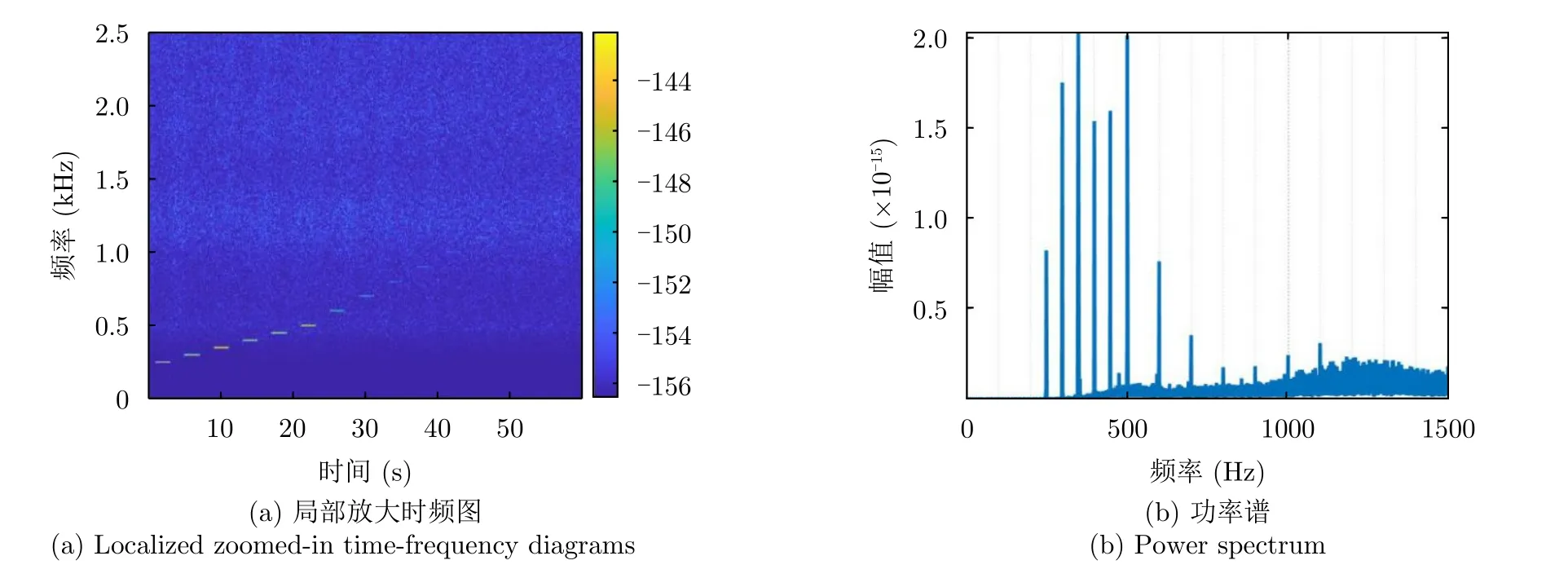
图8 太赫兹雷达探测水下0.2 m声源无干扰单频信号处理频率分析Fig.8 Frequency analysis of interference-free single-frequency signal processing for Terahertz radar detection of underwater 0.2 m sound source
分析式(5)可知,声源频率越高产生的水面振幅越小,对应雷达频段越高,能测到的水面振幅越小。该组对照实验结果验证了太赫兹雷达相比微波雷达在测量声致水面振动时精度更高的优势。
对图6与图8分析可知,在对单频信号的处理结果中,探测到了50~1100 Hz的信号频点,且信号持续时间、间断时间均与发射信号保持一致,而使用卡尔曼滤波准确提取到了100~500 Hz信号频点。1100 Hz以上的信号频点无法被看到,这是因为1100 Hz以上引起水面位移太小,难以被当前系统探测,提高雷达中心频率和缩小发射信号周期能够进一步提高被观测频率范围。按照所建立的理论模型,信号频率从50 Hz到1100 Hz,信号幅度应该随频率增大而减小,其中50 Hz,100 Hz信号幅度小于150 Hz信号,这是由于声源的频率响应导致的,UW30声源技术手册上标注最低发射频率为100 Hz,但实测可以发出100 Hz以下信号,但是发射声压较弱。图6(a)处150 Hz信号相位信息和水面振幅存在较大失真,原因是此处声致水面振幅较大,使回波能量在距离门间发生泄露带来相位噪声所致。
从原始水面振动信号看出,虽然没有加入人为干扰,平静水面状态也会存在微米量级的自然扰动,通过小波阈值法可以很好的滤除。从小波滤波后的水面振动信号看出,雷达相位噪声幅度在1 µm左右,通过卡尔曼滤波后可以很好滤除,也验证了雷达相位噪声符合卡尔曼滤波算法的设定,即雷达相位噪声是一种高斯白噪声,与振动信号无关。
线性调频信号和通信信号的处理过程和单频信号类似,此处只给出最终经过算法处理后的结果,如图9所示。

图9 0.2 m无干扰线性调频信号及BPSK信号处理结果Fig.9 0.2 m interference-free linear FM signal and BPSK signal processing results
在对线性调频信号的处理结果中,可以看出探测信号的变化情况、持续时间、间隔时间均与发射信号保持一致。每组调频信号的幅值均是先逐渐增大,后逐渐减小,这与单频信号变化原因相同,增大部分是由于声源频率响应在100 Hz处较差,减小部分由于信号频率增大引起水面振动幅度减小。
对于通信信号,同样以单频信号和调频信号处理结果为基础,水面振动在低频段效果最好,振动幅度最大,所以设计了载频200 Hz、通信带宽覆盖100~300 Hz的通信信号。从时域波形和时频图中可以看出,信号的变化形式、持续时间与发射信号相似,将最终提取出的水面振动序列进行解调处理,可获得传输的信息。
综上,当声源位于水下0.2 m,水面平静状态时,算法最终的处理结果比较理想,水面波动的干扰信号和雷达带来的相位噪声得到明显的去除。
4.1.3 改变声源深度实验结果
当声源深度分别为水下0.5 m及1.0 m时,对单频信号处理结果如图10和图11所示。

图10 0.5 m声源无干扰单频信号处理结果Fig.10 0.5 m sound source without interference single-frequency signal processing results
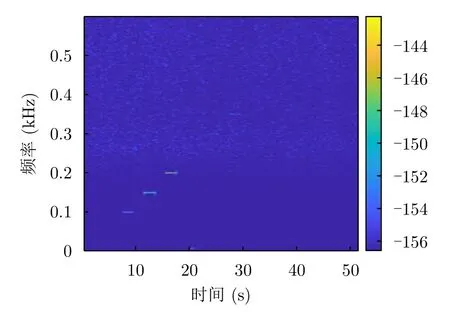
图11 1.0 m声源无干扰单频信号处理结果Fig.11 1.0 m sound source without interference single-frequency signal processing results
可以看到使用实验太赫兹雷达探测系统,在0.5 m水深处探测到最高500 Hz单频信号,计算得振幅85.9 nm。在1.0 m水深处探测到最高350 Hz单频信号,计算得振幅61.3 nm。在4.1.2节实验中,0.2 m水深测得最高1100 Hz信号对应振幅约97.6 nm。比照式(6)可知,声源频率越大,声致水面振动衰减越大,即水面振动扩散范围越小。对应实测结果,尽管低频段信号振幅小,但引起水面振动范围更大,相较高频信号更易检出。以上几组数据说明,本系统及算法对水面低至几十纳米的纹波具有较好的检测能力。
4.1.4 水面加入干扰时的实验结果
声源位于水下0.2 m,声源级不变,使用塑料板对雷达探测区域附近水面进行上下搅动,产生厘米级振幅的小尺度波浪以进行干扰,信号的处理如图12所示。

图12 0.2 m带干扰信号处理结果Fig.12 0.2 m band interference signal processing results
加入人为干扰后,提取出的水面振动信号在信号连续性及高频部分有一定损失,同时存在一定底噪。同时,水面加入干扰后,不再是原来近似的镜面反射,随着水面波动,雷达接收到的回波信号强度也会发生变化,在一维距离像中呈现明暗变化和断续的现象,导致接收信号的连续性受到影响,存在能量泄露的情况,带来较多噪声。从处理结果图中看出,使用本系统及算法在水面加入厘米级振幅的干扰后能够较好的抑制水面自然波动和雷达相位噪声。
4.2 海面试验
雷达探测声致水面微动的海面实验场景如图13所示。大连南部附近黄海水域深度约40 m,水井船前后有两个吊舱,通过定制“L”型声源支架,可以将声源精确降到预设位置。实验选用的声源为鱼唇式声源,该声源具有发射功率大、体积小等优点,最大声源级约为180 dB,适合在海面实验中发射低频声信号。在声源发送信号的同时还需要采用标准水听器监测声源辐射出声信号的波形情况,确保声源辐射出的声信号不存在失真。

图13 海面实验示意及场景图Fig.13 Schematic and scene diagram of the sea surface experiment
由于水面自然干扰低频分量能量较大,且在实测中声源在低频段所发信号波形失真,声源发射信号设置为变化范围为300~500 Hz、步进为50 Hz的单频信号。
4.2.1 一级海况下近岸海面振动提取验证
本次测试选取风浪相对平静海域,调整雷达参数,使回波处于同一距离门内,此时距离分辨率为15 cm。从图14(a)可知,一维距离像内信号幅值差异大,信号连续性差。从图14(b)可知,即使滤除低频信号,原始水面振动包含大量噪声也已不具发射信号特征,在功率谱内已无法观察到待测振动的频率信号。
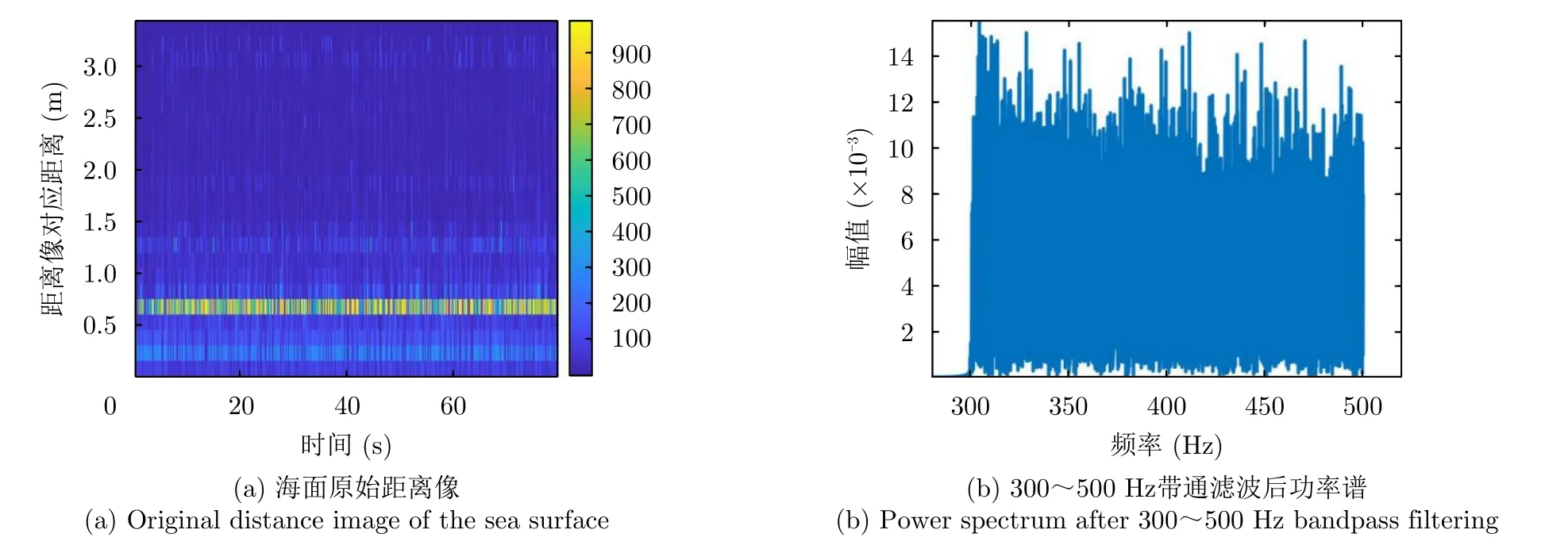
图14 海面起伏距离像及振动信息Fig.14 Sea surface undulation distance image and vibration information
依据本算法对信号进行处理后,使用周期图法进行功率谱密度分析,结果如图15所示。可以看出,经过处理300~500 Hz振动信号的5个频点均被检出,但信号检出的连续性较差且强度较弱,信号中混有较多杂波。因此,在跨介质通信中需要考虑上述存在问题,采用合适的调制方式和校验算法。

图15 0.5 m处300~500 Hz单频信号处理结果Fig.15 Results of 300~500 Hz single-frequency signal processing at 0.5 m
4.2.2 二级海况下强杂波中海面振动提取验证
二级海况下,由图16(a)一维距离相可知探测范围内波浪起伏超过了60 cm,这给微动信号的检出带来巨大的难度,对液面位置进行相位提取后进行原始振动信号的频谱分析,如图16(b)所示,虽然声源在持续发射300 Hz的振动信号,但是从时频图上已看不到任何踪迹,被大量噪声淹没。
在对海面信号依算法进行处理后,在图16(c)时频图中能够看到在300 Hz处有断续的信号亮斑,对信号进行频谱分析如图16(d)所示,在300 Hz处能够看到明显谱峰,说明本系统及算法,在实际海况下,有效地提取到了发射信号,即300 Hz声源在水下0.5 m处引起的极弱的水面振动。使用同样的方法处理,也探测到了350 Hz,400 Hz,450 Hz的信号频点,由于信号较微弱,在时频图中已难以观察到,但在功率谱中能够得到明显且准确的谱线。
4.2.3 采用半物理法推算检测振幅
本算法为从杂波中提取信号,检测到振幅经多级小波分解、阈值量化和卡尔曼滤波,测得信号其幅值难以通过换算对应原始振幅。为验证算法效果,结合4.2.2节二级海况下实测数据,采用半物理法推算从海水中检测到的信号振幅。
在原始振动位移中加入与原始待测信号频率相近的正弦振动信号,改变外加信号幅值,当检测到的振动信号与原始功率谱中信号幅值相等时,认为检出信号与外加振动信号幅值相等。具体地,对于检测处理得到的300 Hz信号,加入与原始信号频率相近的310 Hz正弦振动位移,处理结果如图17(a)和图17(b)所示,此时外加振动信号幅值为130 nm,考虑到原始信号在检测过程中的不连续性,实际声源300 Hz处产生的信号应大于外加信号振幅。
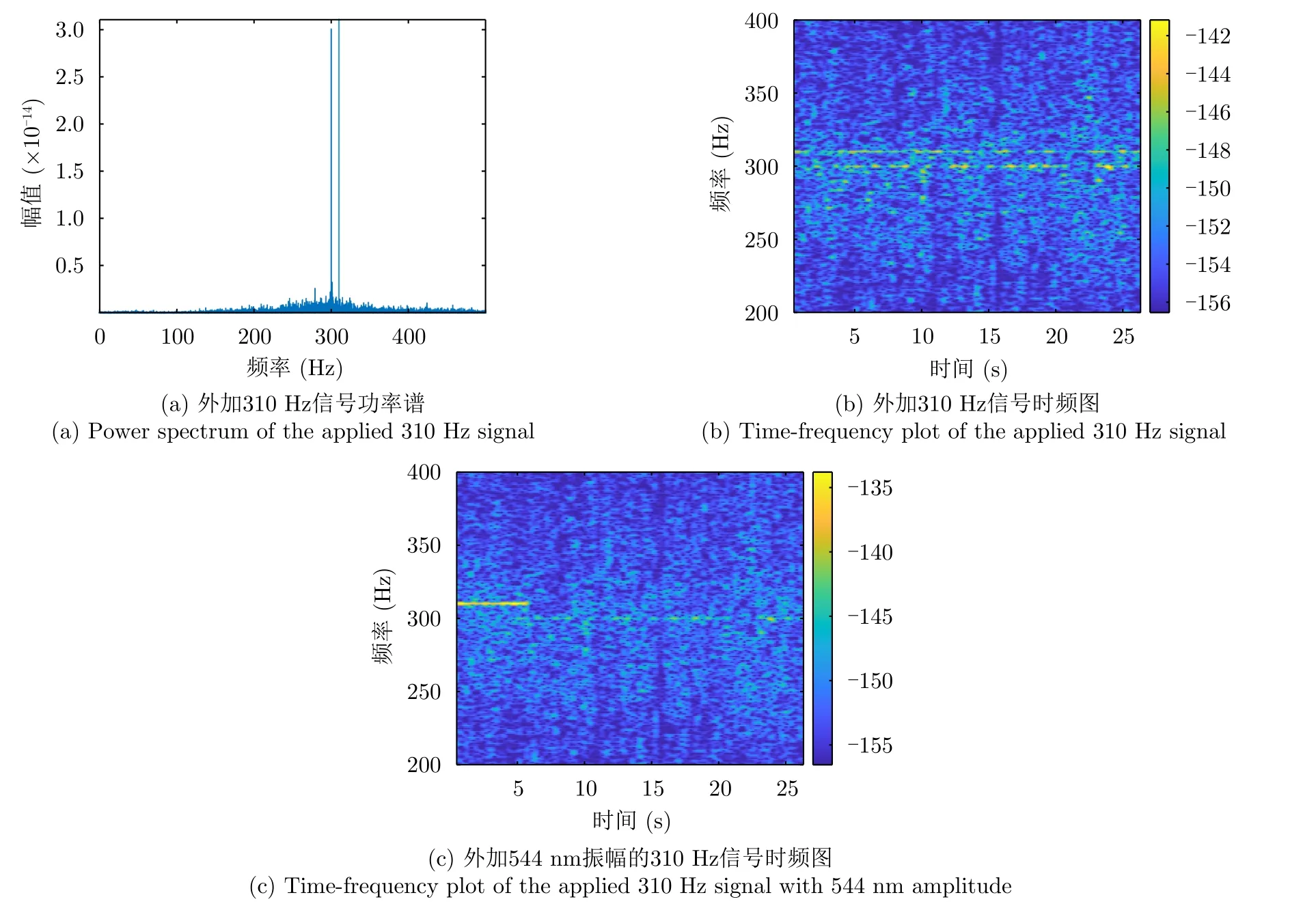
图17 半物理法推算检测振幅Fig.17 Semi-physical method to derive detection amplitude
经监听器标定,发送300 Hz信号时声源级为171.6 dB。参考点声源计算此处振幅约为544 nm,而外加振幅544 nm的310 Hz频率信号达到相同功率谱幅值,如图17(c),需要占整个信号周期的约21.6%,反映了检出完整幅值信号的大致占比,即检测到的有效信号占比至少为21.6%。
5 结语
本文分别从理论和实验两方面研究了基于太赫兹雷达的声致水面微动信号检测技术,建立了声致水面的理论模型,提出了小波-卡尔曼信号滤波方法,进行了太赫兹雷达探测声致水面微动的实验研究。结果表明:太赫兹雷达凭借波长小、相位敏感度高的特性,能够成功探测提取到声致水面的振动信号;声致水面实际的运动形式与建立的理论模型在运动趋势上一致,证明了理论模型的正确性;通过小波-卡尔曼信号滤波算法处理,提取的信号能够有效地去除水面自然波动的干扰和雷达的相位噪声,并通过理论计算及半物理法外推,验证了系统对静水面十纳米级振幅信号及二级海况下亚微米(百纳米)级振幅的声致水面振动信号具有较强的检测能力和较高的信号分辨率,证明了所提算法的有效性。上述方法为我国海洋环境下近距离水空跨介质通信试验成功提供了关键支撑,同时在未来水下潜航器探测等领域具有重要的应用前景。
致谢感谢中国船舶重工集团七六〇所、西北工业大学、中船海洋探测技术研究院在实验测量方面提供的帮助。
