基于模糊聚类与用户兴趣的协同过滤推荐算法

郭晓宇，沈宇麒，崔 衍

（南京邮电大学 物联网学院，江苏 南京 210003）

0 引言

随着数字技术和社交网络的快速发展，人们进入了大数据时代，科学技术的发展让人们的生活和交流越来越便捷。但是，信息过载的问题也日益突出，用户很难从大量数据中找到自己感兴趣的信息。因此，如何高效地提取有用信息成为当前信息技术的热门研究领域。为了解决该问题，推荐系统发挥了重要作用。

推荐系统被广泛应用于电影、新闻、音乐、社交网络等方面，为亚马逊、淘宝等大型电子商务公司提供更好的用户体验［1-2］。推荐系统可分为基于内容的推荐系统［3］、协同过滤推荐系统［4］和混合推荐系统［5］。目前，协同过滤算法是推荐系统中非常流行的方法，广泛应用于大数据挖掘、电子商务等领域。协同过滤算法通过分析用户行为，利用用户或物品之间的相似性确定最近邻居集，然后利用最近邻居集预测当前用户的偏好和评分［6］。与基于用户或物品的推荐算法相比，其具有速度快、效率高、鲁棒性强等优点，推荐结果通常比其他算法更加准确。协同过滤推荐算法可分为基于记忆的推荐算法和基于模型的推荐算法，其中基于记忆的推荐算法也称为基于邻域的推荐算法，其又可分为基于用户和基于物品的协同过滤推荐算法。与基于记忆的推荐算法不同，基于模型的推荐算法主要采用数据挖掘或机器学习等方法在用户评分矩阵上建立预测模型。

然而，传统协同过滤推荐算法容易出现的用户数据的稀疏性、可扩展性较差以及冷启动等问题在实际应用中仍然普遍存在，严重影响了推荐算法的推荐质量。

1 相关研究

为了解决上述问题，文献［7］将聚类引入到协同过滤推荐算法中，通过K-means 算法对数据进行预处理，采用一种基于中心的方法寻找邻居，在一定程度上解决了传统协同过滤推荐算法中存在的可扩展性以及数据稀疏性问题。文献［8］提出一种基于项目聚类和全局相似度的协同过滤推荐算法，使用K-means 方法对物品进行聚类，在每个聚类中计算局部相似度，并引入一个重叠因子进行优化，最后结合全局相似度对物品进行预测，提高了推荐算法的准确度。文献［9］提出一种双向聚类的协同过滤推荐算法，使用K-means 聚类方法分别从用户和项目两个方向进行聚类，并在两个簇中分别使用改进的相似度进行协同过滤推荐，有效提高了推荐精度。文献［10］提出一种新的协同过滤推荐算法，通过在协同过滤中引入信息熵和双聚类来提取局部密集评分模块。该算法首先对用户项目评分矩阵进行双聚类分析，以识别其密集的局部模块，然后计算每个聚类的信息熵以实现基于用户的协同过滤推荐算法，最后将该算法与基于项目的协同过滤推荐算法进行加权结合。实验结果表明，该算法缓解了数据稀疏性，提高了推荐的准确性和计算效率。文献［11］提出一种基于聚类和模拟退火的协同过滤推荐算法，使用模拟退火算法对K-means 聚类算法进行改进，定义了一个用户类型向量并将其用作聚类对象。实验结果表明，该方法具有较高的推荐准确率。文献［12］结合了降维和聚类方法，首先通过K-means 算法对用户进行聚类，然后利用奇异值分解（Singular Value Decomposition，SVD）对每个聚类进行降维。文献［13］采用聚类和人工神经网络（Artificial Neural Network，ANN）解决协同过滤中的数据稀疏问题。该算法首先对用户评分数据进行预处理，其中包括特征选择、归一化以及使用主成分分析法（Principal Component Analysis，PCA）进行降维等步骤，然后采用K-means 聚类方法将结果输入ANN 进行处理，得到最后的推荐列表。该方法有效解决了稀疏性问题，提高了推荐质量，具有良好的预测精度。文献［14］采用一种基于SVD 与模糊聚类的协同过滤推荐算法，首先通过SVD 方法对用户物品评分矩阵进行降维处理，然后利用模糊聚类算法对用户进行聚类。文献［15］提出一种融合隐式语义算法和模糊聚类算法的协同过滤推荐算法，降低了数据稀疏性，提高了推荐算法的准确度。文献［16］提出一种基于模糊聚类和监督学习模型的高效混合推荐系统，其中将模糊聚类技术应用于基于项目的协同过滤框架中，解决了冷启动问题，最后与基于内容的推荐算法进行融合，为用户提供个性化的推荐结果。实验结果证实了该算法的优越性。文献［17］引入一种权重调节机制并结合用户偏好等隐性反馈信息，提升协同过滤推荐算法的准确度。

通过以上分析可以看出，聚类方法在基于用户的推荐算法中很常见，能有效提高推荐算法的准确度。另外，用户的兴趣偏好也是需要考虑的因素之一。文献［18］提出一种基于项目特征与用户兴趣模糊性的推荐算法，通过构建项目特征隶属度矩阵和用户类别偏好矩阵构建用户兴趣模型，以进一步提高推荐的准确度。文献［19］分析了用户对物品的情感偏好，从而计算用户之间的相似程度，最后进行评分预测和物品推荐。该算法提高了推荐的准确性，降低了算法的时间复杂度。文献［20］提出一种融合用户兴趣和评分差异的协同过滤推荐算法，将TF-IDF（Term Frequency-Inverse Document Frequency）思想引入用户兴趣偏好中，并且使用时间窗口的指数衰减函数进一步改善用户的兴趣偏好。

以上文献都表明在协同过滤推荐算法中，用户的兴趣偏好在一定程度上能提高推荐的准确度。通常物品可以同时具有一种或多种类型，如果两个用户对同一类型的物品访问次数越相近，表明两个用户越相似。由此，本文提出一种基于模糊聚类与用户兴趣的协同过滤推荐算法，该算法结合用户的局部兴趣和全局兴趣，综合得到用户的兴趣偏好，然后对用户兴趣偏好进行模糊聚类，并使用粒子群算法优化模糊聚类初始聚类中心。为了缓解用户评分矩阵的稀疏性，使用聚类用户中对该物品的评分均值进行填充。最后，通过对用户评分相似度和用户兴趣偏好相似度进行加权结合，得到改进的用户相似度，从而构建用户相似度矩阵。通过在聚类中选择最近邻居对物品进行预测评分，实验结果表明，本文算法相比传统的协同过滤推荐算法具有更高的推荐准确度。

2 相关技术

2.1 基于用户的协同过滤推荐算法

基于用户的协同过滤推荐算法假设用户的兴趣爱好是相对稳定的，然后根据目标用户的最近邻居进行预测评分。以用户观看电影为例，如果某些用户和目标用户都观看了相同的几部电影，那么这些用户和目标用户则表现出相似的用户偏好，计算每个用户与目标用户之间的相似度值并进行排序。设置邻居数为N，则前N个用户为目标用户的最近邻居集合。最后，通过最近邻居集合预测用户对未知电影的偏好程度。该算法主要包括以下几个步骤：

步骤1：构建用户—物品评分矩阵。假设U={u1，u2，u3，…，un}为用户集，I={i1，i2，i3，…，im}为物品集，rukil表示用户uk(k∈n，uk∈U)对物品il(l∈m，il∈I)的评分。Rnm为用户—物品评分矩阵，每行对应一个用户，每列对应一个物品，行和列的交点为该用户对此物品的评分，其中0 表示该用户没有对物品进行评分。Rnm用户—物品评分矩阵如式（1）所示：

步骤2：相似度计算。根据用户—物品评分矩阵可以计算用户与目标用户的相似度，从而构建用户相似度矩阵。相似度计算有以下几种方法：

（1）杰克逊相似度。

（2）余弦相似度。

（3）皮尔逊相似度。计算相似度最常用的方法是皮尔逊相似度方法，其可以衡量两个变量之间存在线性关系的程度。本文提出的基于模糊聚类与用户兴趣的协同过滤推荐算法即采用皮尔逊相似度计算方法。

其中，Iu、Iv分别表示用户u和用户v评分的物品集合，rui、rvi分别表示用户u和用户v对物品i的评分分别表示用户u和用户v评分物品的平均得分。

2.2 模糊C均值聚类算法

在基于用户的协同过滤推荐算法中，经常使用Kmeans 等聚类算法把相似的用户聚类在一起，在目标用户所在聚类中选择最近邻居，可以很好地提高推荐质量。而模糊C 均值聚类（Fuzzy C-means Clustering，FCM）算法不同于K-means 等硬聚类算法，其是软聚类算法。在对样本的聚类过程中，FCM 算法并不是单一地将样本归属于某一类别，而是通过模糊理论，将样本划分到多个类中。

FCM 算法使用隶属度表示每个样本属于每个聚类的程度，然后根据隶属度大小将样本集中的每一个样本模糊划分到不同聚类中。通过不断更新每个聚类中心，使得目标函数值达到最小值。假设样本集为X={x1，x2，…，xn}，将其样本划分为p类(1 ≤c≤n)，聚类中心为C={c1，c2，…cp}。μik表示样本点xk属于聚类中心ci的隶属度值，μik∈[0，1]，隶属度值的大小满足以下条件：

经过FCM 算法进行聚类后，会输出p个聚类中心向量和一个n×p维的模糊隶属度矩阵U。

FCM 算法有两个重要参数：一是聚类类别个数p，二是模糊指数m，用于调整聚类模型的模糊程度，通常m的值为2。如果m值过大，则聚类效果较差；如果m值太小，则聚类效果更接近K-means 聚类。FCM 算法的目标函数如式（6）所示：

J(U，C)描述了所有样本到所有聚类中心的距离。其中，U表示隶属度矩阵，U=[μik]，μik∈[0，1] ；C表示聚类中心矩阵，C=[ci]，i=1，2，…，p；‖ ‖xk-ci表示样本xk到聚类中心ci的欧式距离。当目标函数满足约束条件时，利用拉格朗日函数构造分类矩阵与聚类中心的迭代表达式，然后通过多次迭代，得到目标函数的全局最小值，即最优的聚类结果。

FCM 算法步骤如下：

（1）确定聚类类别个数c、模糊指数m和迭代次数T。

（2）随机初始化隶属矩阵U或初始聚类中心C。

（3）根据式（8）更新隶属度矩阵和聚类中心。

（4）计算两个相邻目标函数的差值，当J(i+1)-J(i)＜δ，即小于指定阈值，或迭代次数达到最大值时，得到最优的聚类中心C和隶属度矩阵U，否则返回步骤（3）继续迭代，直到满足结束条件为止。

2.3 粒子群优化算法

PSO（Particle Swarm Optimization，PSO）算法是一种群体智能的优化算法，最早起源于对鸟类觅食行为的研究，通过群体中个体之间的协作和信息共享来寻找最优解。在PSO 算法中，粒子也称为个体，分布在多维搜索空间中，每个粒子或个体都表示一个可行解。在迭代计算过程中，通过比较每个粒子的个体适应度值大小来更新每个粒子的个体极值和全局极值，最终得到最优解。

假设粒子数量为n，每个粒子的位置可表示为X=[x1，x2，…，xn]，每个粒子的速度可表示为V=[v1，v2，…，vn]，则第i个粒子的位置可表示为xi(i∈[1，n])。第i个粒子的速度为vi，其个体极值为pbesti，群体的全局极值为gbesti。那么每一个粒子可通过式（10）、式（11）更新自己的速度和位置。

其中，w表示动态权重；c1、c2表示加速系数，通常设置为2；r1、r2是随机数，r1，r2∈[0，1]。

3 本文算法

在传统的协同过滤推荐算法中，核心思想是寻找用户的相似邻居。如果用户的大多数邻居都喜欢某个物品，则会向目标用户推荐该物品。从用户的角度来说，如果两个用户多次选择同一个物品，则说明两个用户具有相同的兴趣偏好。本文围绕用户兴趣，提出一种基于模糊聚类与用户兴趣的协同过滤推荐算法，该算法通过结合用户兴趣偏好的相似性来解决用户评分矩阵中的稀疏性问题，并使用了改进的FCM 模糊聚类算法来解决推荐阶段的可扩展性问题。

为了解决数据稀疏性问题，本文提出一种矩阵填充方法。该方法首先通过对用户兴趣偏好进行模糊聚类，将具有相似兴趣偏好的用户聚到一起，得到用户的聚类结果。然后，根据用户—物品评分矩阵缺失值寻找到同一个聚类中对该物品评分的用户，通过计算其评分均值来填充用户物品评分矩阵，从而产生密集的用户—物品评分矩阵。为了解决可扩展性问题，本文使用FCM 模糊聚类算法对用户进行聚类，由于FCM 算法存在陷入局部极小值问题，采用PSO 算法对初始聚类中心进行优化，进一步改进模糊聚类算法。最后，在推荐阶段选择用户在聚类中的最近邻居来预测该用户对物品的评分。本文算法框架如图1所示。

Fig.1 Improved collaborative filtering recommendation algorithm图1 改进的协同过滤推荐算法

3.1 数据预处理

3.1.1 用户—类别矩阵构建

用户—类别矩阵由每个用户访问每一类别的次数组成。U={u1，u2，u3，…，un}为用户集，C={c1，c2，c3，…，cp}为物品的类型集合，n为用户个数，p为物品类型个数。Cnp为用户—类别访问矩阵，如式（12）所示。其中，tuicj表示用户ui对类别cj的访问次数，0 表示该用户没有访问该类别的物品。

3.1.2 用户—兴趣偏好矩阵构建

根据用户—类别矩阵可以知道每个用户对每个类型的访问次数。实际上，如果两个不同用户对某个类别的访问次数相同，并不能说明两个用户的兴趣是一样的，而是需要通过用户访问率来进一步了解用户偏好。例如：用户u1和用户u2对类型c的访问次数都为20，对所有类型的总访问次数分别为50和200，用户访问率分别为40%和10%，则说明用户u1更喜欢类型c。但是，用户偏好还会受到类别访问率影响，例如：类型c1与类型c2的总访问次数分别是60和15，所有类型的访问次数为300，则c1与c2的类别访问率分别为20%和5%。如果用户u对c1与c2的访问率分别为40%和20%，从用户访问率来看，会认为用户u更喜欢类型c1，但是从类别访问率总体来看，发现与其他用户相比，其更喜欢类型c2。为了解决以上问题，本文结合了用户局部兴趣和全局兴趣综合得到用户—兴趣偏好矩阵。

（1）用户的局部兴趣。用户的局部兴趣矩阵可以通过用户对物品的偏好程度来表示。通常，用户和物品之间的交互频率大小可用来表示用户对物品的偏好程度。用户对某个类型的偏好可通过用户对该类型访问次数占用户对所有类型访问次数的比值来表示。如式（13）所示：

从用户物品的评分上看，用户对物品的评分越高，则用户对该类型的偏好程度也应该越高，通过引入一个评分权重向量对用户类型偏好进行优化。改进后的用户类型偏好度也即用户的局部兴趣如式（14）所示：

（2）全局兴趣偏好。为了找到每个用户兴趣偏好密集的物品类别，本文定义了一个全局兴趣偏好度，可以得到每个物品类型的访问度，如式（15）所示：

（3）用户的综合兴趣偏好矩阵。考虑到用户的局部兴趣和全局兴趣，可以得到用户的综合兴趣偏好矩阵，如式（16）所示：

其中，LR表示用户的局部偏好度，G表示全局兴趣。

3.2 改进的模糊C均值聚类算法

在实际生活中，用户可能同时有多种兴趣偏好，具有不确定性，所以本文使用FCM 模糊聚类算法对用户进行聚类。FCM 模糊聚类算法运用模糊概念，通过计算用户对聚类类别的隶属度大小对用户进行分类。然而，传统的FCM算法很大程度上依赖于初始聚类中心的选取，容易陷入局部最优，从而影响算法的聚类效果。粒子群优化算法是一种群智能优化算法，具有很强的全局搜索能力。由于其具有算法简单且效率高等优点，被广泛应用于许多优化问题中。因此，为了解决以上问题，本文将粒子群优化算法引入模糊聚类，对FCM 算法随机选取初始聚类中心进行优化处理。算法优化步骤如下：

步骤1：给定粒子群数目n，聚类个数k，模糊指数m，迭代次数T。

步骤2：随机初始化聚类中心，对聚类中心进行编码并赋值给各个粒子，每个粒子代表各类的聚类中心。

步骤3：通过式（6）计算每个粒子的适应度值，更新个体极值。

步骤4：根据每个粒子的个体极值，找到全局极值以及全局极值的位置。

步骤5：根据式（10）、式（11）更新每个粒子的速度和位置，产生新一代个体。

步骤6：若满足终止条件，则算法结束，输出最优值即最佳的聚类中心，否则返回步骤3继续执行。

3.3 矩阵填充方法

在同一个聚类中，用户偏好在一定程度上具有相似性。本文对用户—兴趣偏好矩阵使用改进的FCM 模糊聚类算法，根据用户兴趣偏好的相似性对相似的用户进行聚类。对于用户—物品评分矩阵中的缺失值，首先找到用户所属聚类类别，然后在聚类中选择对该物品评分的用户，通过求取评分的均值，可以得到目标用户对该物品的预测分数。算法步骤如下：

步骤1：输入用户—评分矩阵Rnm、用户—兴趣偏好矩阵Cnp。

步骤2：使用改进的FCM 算法对用户—兴趣偏好矩阵进行聚类。

步骤3：对用户—物品评分矩阵中的每一个缺失值，找到该用户所属聚类的其他用户。

步骤4：计算聚类中所有对该物品评分的用户平均分，填充用户—物品评分矩阵中的缺失值。

步骤5：输出密集的用户—物品评分矩阵R'。

该方法流程如图2所示。

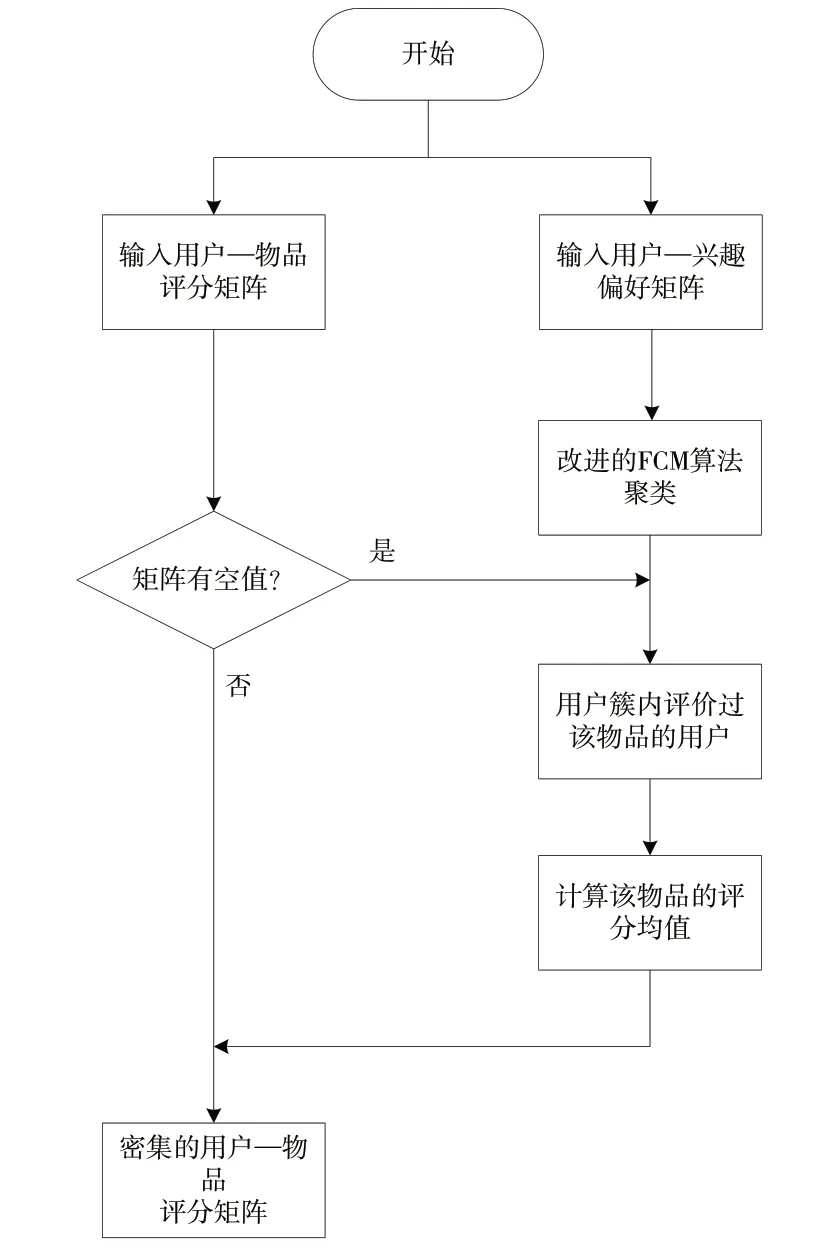
Fig.2 Matrix filling method flow图2 矩阵填充方法流程

3.4 相似度计算

相似度计算是协同过滤推荐算法的核心，而相似度计算方法直接影响用户最近邻居的选择和推荐算法效率。为了计算用户相似度，本文提出的算法通过对用户物品评分相似度和用户兴趣偏好相似度进行加权求和，其中既包含了用户物品评分矩阵的显式信息，又考虑了用户对物品兴趣偏好的隐式信息。

本文使用基于用户的皮尔逊相似度计算方法，通过用户物品评分矩阵可以得到用户物品的评分相似度，如式（17）所示：

通过用户兴趣偏好矩阵，可以得到用户兴趣偏好的相似度。考虑到物品的流行度以及类型偏好的影响，引入一个物品类型惩罚因子，如式（18）所示：

其中，n表示用户数量，|Nci|表示对物品类型ci给出的评分大于等于4 的用户个数。改进的用户兴趣偏好相似度如式（19）所示：

其中，Cuv表示用户u和用户v共同访问的物品类型，gui、gvi分别表示用户u和用户v对类型ci的偏好分别表示用户u和用户v的平均偏好。

将用户物品评分相似度和用户兴趣偏好相似度进行加权结合，可以得到最终的用户相似度计算公式，如式（20）所示。其中，α为权重系数，取值范围为［0，1］，用于调整用户评分相似度和用户兴趣偏好相似度的所占权重。

3.5 预测分数

通过相似度计算可以得到用户相似度矩阵，用户的相似度值越大，则表示两个用户越相近。寻找最近邻居是协同过滤推荐算法中最重要的一步，本文通过改进的模糊聚类方法将用户分为不同簇，在同一簇内选取与目标用户相似度值最高的用户作为最近邻居集合，记为N，则用户u对项目i的评分可表示为：

其中，Pui表示用户u对物品i的预测得分分别表示用户u和用户v的平均得分，rvi表示用户v对物品i的评分，sim(u，v)表示用户u和用户v的相似度值，N表示用户u的邻居集(v∈N)。

4 实验及结果分析

4.1 实验数据集

为了验证改进推荐算法的有效性，本实验使用MovieLens 100K 公共电影评分数据集，该数据集包含了用户信息、电影信息以及用户对电影的评分信息等。将数据集分成80%的训练集和20%的测试集，数据集具体信息如表1所示。

Table 1 MovieLens 100K dataset information表1 MovieLens 100K数据集信息

其中，MovieLens 100K 数据集包含19 个电影类型：动作、冒险、动画、儿童、喜剧、犯罪、记录、戏剧、幻想、黑色电影、恐怖、音乐剧、神秘、爱情、科幻、战争、惊悚、西部以及其他。每部电影可以是一种类型，也可以是多种类型。为了更好地区分电影类型，本文去掉“其他”类别，选取剩余的18个电影类型作为类别属性。

4.2 实验评估标准

推荐算法使用最广泛的评估标准之一是平均绝对误差（Mean Absolute Error，MAE）。MAE 是衡量预测准确率的指标，表示算法评分与真实评分之间的差距。该值越小，则表示预测准确度越高，推荐质量越好，越符合用户兴趣。本文以MAE 作为衡量算法推荐准确性的评价指标，分数预测集中的元素个数用N表示，预测分数与实际分数分别用P和R表示。MAE 可表示为：

4.3 实验结果分析

本文改进算法所涉及的参数有用户相似度的权重系数α、聚类个数k。

4.3.1 权重系数的影响

权重系数可以调整用户物品评分相似度和用户兴趣偏好相似度所占权重，通过MAE 值的大小选取最佳的α值。MAE 值越小，算法性能越高。实验参数设置聚类个数k=5，邻居个数N=30。随着α的增加，MAE 值的变化趋势如图3 所示。由图可以看出，当α的值小于0.2 时，MAE值呈下降趋势；当α的值大于0.2 时，随着α的增大，MAE值也逐渐增大。当α=0.2 时，MAE 值最小，则α权重系数的最佳取值为0.2。

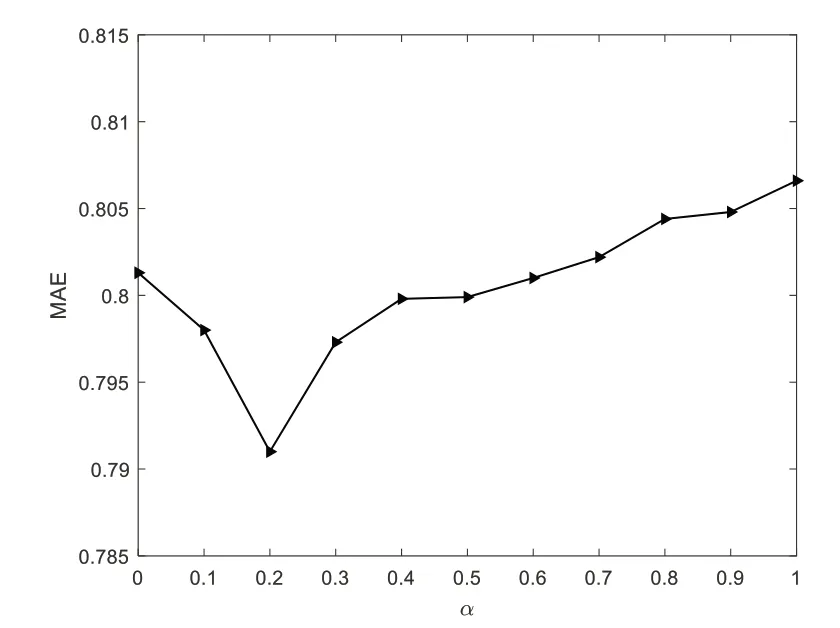
Fig.3 Influence of similarity weight α value图3 相似度权重α值的影响

4.3.2 聚类个数k的影响

用户聚类个数k值也是影响算法性能的因素之一，当聚类用户个数较少时，每个用户分类比较模糊，当聚类用户个数较多时，同一聚类中可能只有较少的用户，这些都会影响推荐算法的精度。设置实验参数α=0.2，邻居个数N=30，使用平均绝对误差MAE 值作为算法性能的评价标准。实验结果如图4 所示，当k∈[2，4]时，MAE 值逐渐下降；当k∈[4，5]时，MAE 值逐渐上升。随着k继续增大，MAE 值整体呈上升趋势。所以当k=4 时，MAE 值最小，用户聚类的最佳k值为4。

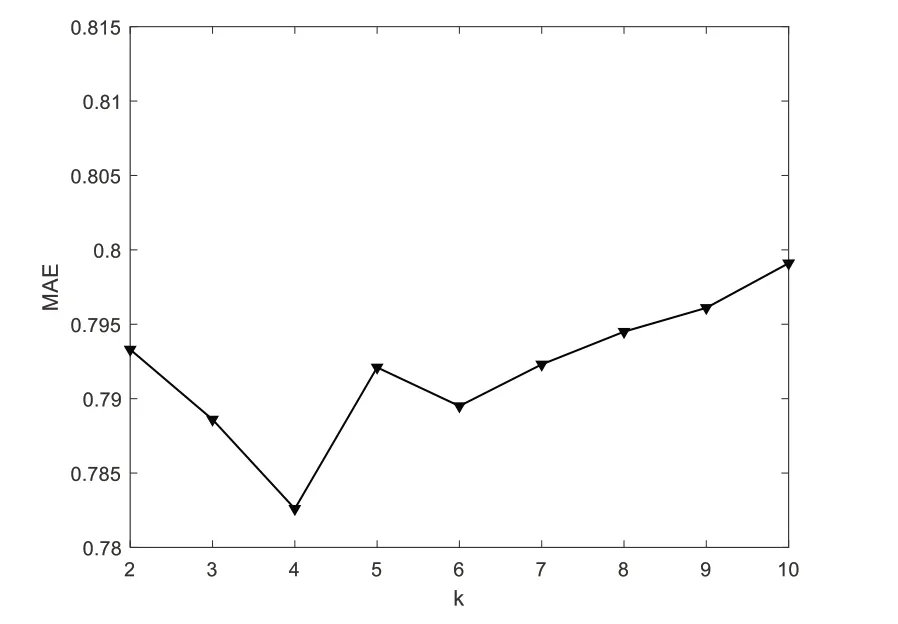
Fig.4 Influence of cluster number k图4 聚类个数k值的影响

3.3.3 优化的聚类效果对比本文使用粒子群算法对FCM 算法初始聚类中心进行优化。考虑到优化的聚类对整个算法准确度的影响，将使用FCM 聚类和粒子群优化的FCM 聚类（PSO-FCM）应用于推荐算法的性能进行对比，并使用MAE 值作为优化效果的评估标准。设置实验参数α=0.2，邻居个数N=30，实验结果如图5所示。

Fig.5 Comparison of two clustering algorithms图5 两种聚类算法效果对比

由图5 可见，当使用FCM 聚类时，随着聚类个数的增加，MAE 值先减小后增大，当k=3 时，MAE 值最小，随后整体呈上升趋势；当使用PSO-FCM 聚类时，MAE 值也呈先减小后增大的趋势，当k=4 时，MAE 值最小。这是因为PSO-FCM 聚类算法使用粒子群算法找到了最优的初始聚类中心，可有效避免聚类陷入局部最优，再通过优化的FCM 算法进行聚类，从而提高了推荐算法的准确度。

4.3.4 实验对比

为了验证本文提出的基于模糊聚类与用户兴趣的协同过滤推荐算法的性能，将本文提出的改进算法命名为FCMP-CF，实验设置α=0.2，k=4，并与其他3 种算法进行实验对比分析，分别是传统基于用户的协同过滤推荐算法（User-CF）、基于FCM 用户聚类的协同过滤推荐算法（FCM-CF）以及文献［17］提出的融合权重调节和用户偏好的协同过滤推荐算法（WAUP-CF）。当N=5 时，实验结果如表2所示。4种算法比较如图6所示。

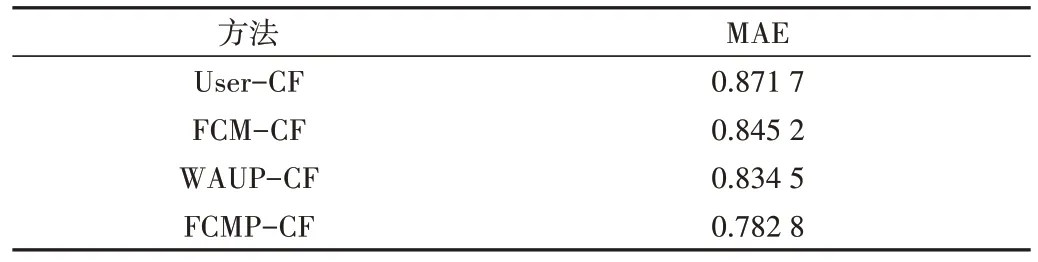
Table 2 Comparison results of four methods表2 4种方法比较结果

通过以上实验可以看出，随着邻居个数N 值的增大，相比于传统基于用户的协同过滤推荐算法，本文算法的平均绝对误差降低了8.9%，相比于基于FCM 用户聚类的协同过滤推荐算法，降低了6.2%，相比于融合权重调节和用户偏好的协同过滤推荐算法，降低了5.2%。综合得出，本文算法的MAE 值在整体范围内小于另外3 种协同过滤推荐算法，算法性能最优，推荐准确率更高。

其中，传统基于用户的协同过滤推荐算法（User-CF）由于没有考虑用户的聚类方法，并且评分矩阵非常稀疏，其MAE 值最大，推荐效果不佳。基于FCM 用户聚类的协同过滤推荐算法（FCM-CF）将评分相似的用户聚在一起，在聚类中选择最近邻居，在一定程度上改善了传统基于用户的协同过滤推荐算法的不足，推荐效果有所提升。融合权重调节与用户偏好的协同过滤推荐算法（WAUP-CF）考虑了用户相似度和用户偏好相似度，通过对相似度进行改进，提高了推荐算法的准确度，但是没有考虑用户的全局兴趣以及用户评分矩阵的稀疏性。而本文提出的基于模糊聚类与用户兴趣的协同过滤推荐算法引入用户兴趣偏好度，并且对用户兴趣进行了优化。通过对用户兴趣偏好的聚类，利用具有相似偏好的用户平均值填充用户评分矩阵，再结合改进的用户兴趣偏好相似度和用户评分相似度，得到综合的用户相似度，从而构建用户相似度矩阵，最后在聚类中选择最近邻居对目标用户进行推荐。该算法引入了用户偏好并且缓解了数据稀疏性，具有更高的推荐准确度。

5 结语

针对传统协同过滤推荐算法中存在的数据稀疏性和推荐准确度低等问题，本文提出基于模糊聚类与用户兴趣的协同过滤推荐算法。在构建用户兴趣矩阵时，通过优化用户的局部兴趣，同时结合全局兴趣，能够更加准确地反映出用户兴趣偏好，对用户的聚类也更加准确。另外，使用粒子群算法对模糊聚类算法进行优化，对用户兴趣偏好进行模糊聚类，将具有相似偏好的用户聚类在一起。对于用户—物品评分矩阵的缺失值，使用聚类中对该物品评分的用户均值进行填充，有效缓解了数据的稀疏性。然后，使用改进的基于用户物品评分和用户兴趣偏好的相似度预测目标用户对物品的评分，形成最终的推荐列表。实验结果表明，与传统的协同过滤推荐算法相比，本文提出的算法在一定程度上提高了推荐的准确性。