基于超大涡模拟的燃烧室气动性能仿真研究进展
2023-09-14张宏达韩省思刘太秋马宏宇任祝寅
张宏达 ,韩省思 ,刘太秋 ,朱 健 ,马宏宇 ,任祝寅
(1.中国航发沈阳发动机研究所,沈阳 110015;2.南京航空航天大学能源与动力学院,南京 210016;3.清华大学航空发动机研究院,北京 100084)
0 引言
燃烧室是航空发动机的核心部件之一,燃烧室气动性能对整机性能起到至关重要的作用[1-2]。为了满足发动机对燃烧室日益严苛的技术要求,燃烧室内部燃烧组织模式以及流动特性都变得十分复杂。扩压器减速增压过程可能面临强逆压梯度下流动分离;气流经过多级旋流装置形成大尺度涡旋结构,一方面促进液体燃料雾化蒸发,与燃料形成强脉动、非定常混合气,另一方面生成气动回流区驻定火焰;主燃/掺混孔多股射流与火焰筒内横向来流相互作用,形成反向旋转涡对,对湍流混合有重要影响。在流动基础上,雾化蒸发、掺混、化学反应、湍流与火焰相互作用等多尺度物理化学过程强烈耦合,共同决定了燃烧室气动特性,这些物理化学过程的高精度建模和计算一直是国内外研究的热点问题。
燃烧室中雾化蒸发、掺混和燃烧过程是在湍流流动环境下发展演化的,因此流动是燃烧室气动性能仿真的基础[3]。湍流基本特征是由于非线性对流过程导致流动参数呈现随机脉动,湍流包含众多涡系结构,不同涡系在长度和时间尺度的跨度巨大,并且随着雷诺数增大,各尺度之间的跨度急剧增大。根据湍流涡系结构被直接求解的比例,湍流模拟方法划分为直接数值模拟(Direct Numerical Simulation,DNS)、雷诺平均(Reynolds-Averaged Navier-Stokes,RANS)、大涡模拟(Large Eddy Simulation,LES)和混合湍流模拟方法。工程中广泛应用的RANS 方法对湍流平均场进行求解,采用模型模化全部湍流脉动信息,计算量小,但精度较差,对于燃烧室中强旋流和非定常流动过程,RANS 不能满足精细化设计要求。Pitsch[4]指出,LES 计算量介于RANS 和DNS 之间,目前应用于中低雷诺数非受限空间湍流燃烧计算。由于燃烧室近壁区湍流尺度小,流动雷诺数高,仅燃烧室单个头部的LES计算所需网格量在数亿至数十亿量级,如此高的计算资源消耗限制了LES 在燃烧室仿真中广泛使用[5]。基于超大涡模拟方法(Very Large Eddy Simulation,VLES)和混合雷诺平均-大涡模拟方法(Hybrid RANS-LES Method)框架建立高精度计算模型和方法,是数值仿真的重要趋势[5-6]。Han 等[7-9]发展的VLES方法解决了传统LES中过滤网格尺度和求解湍流尺度匹配限制导致的计算效率低问题,实现了湍流多尺度特性、瞬态演化特性以及网格分辨率之间的耦合建模,VLES依据涡系结构演化的实时特征,自适应调整湍流求解和模型模化之间的比例,在保证计算精度的条件下,显著降低计算成本。
尽管如此,与传统LES相比,VLES的理论及特性尚未得到广泛研究和使用。本文系统介绍VLES 的模化理论及其在燃烧室相关多种物理场景下的使用效果,促进VLES 在航空发动机燃烧室仿真领域的规模化应用。
1 超大涡模拟方法
湍流模拟方法对计算资源消耗及模型影响如图1所示,RANS、LES和VLES方法均通过湍流建模实现流动仿真。需要说明的是,VLES 最早的明确定义由Pope[6]给出,指的是“计算网格尺度太粗糙从而使直接求解的湍流动能小于总湍流动能的80%"。同时Pope给出的LES 含义[6]是“计算网格很精细从而使直接求解的湍流动能大于总湍流动能的80%”。尽管如此,需要特别说明的是,本文介绍的VLES 是在前期基础上重新模化发展的新型计算方法。虽然命名一样,但新的VLES 方法与Pope定义的VLES 方法具有本质上的不同。从图中可见,传统的湍流模式按计算精度依次为RANS、URANS、hybrid RANS/LES、LES、DNS,在新的模型框架下,湍流模式划分按计算精度依次为RANS、VLES、DNS,即VLES 方法实现了多种传统湍流模式的统一,不同模型在实际计算中依据局部特征自适应光滑过渡和转换。

图1 湍流模拟方法对计算资源消耗及模型的影响
与RANS 和LES 方法相比,VLES 建模中考虑了更多的特征尺度,不同湍流模拟方法建模中的特征尺度见表1。从表中可见,积分尺度、湍流截断尺度和Kolmogorov尺度(最小湍流尺度)等3个具有代表性的湍流尺度,能够整体考虑流场的多尺度特征。RANS方法仅考虑了流场中最大尺度(即积分尺度),未描述湍流小尺度结构;LES 方法考虑了与网格尺度直接相关的截断尺度,但模型中没有体现湍流尺度的影响,因此LES结果严重依赖于计算网格,为得到高精度的计算结果,需要划分很细密的网格。

表1 不同湍流模拟方法建模中的特征尺度
VLES 方法的本质是通过引入分辨率控制函数Fr,对传统的RANS湍流应力进行重新模化,通过雷诺应力衰减可以得到亚格子尺度湍流应力张量[10]。Speziale[11]最早提出了分辨率控制函数Fr的模型,但原始模型存在以下缺陷:(1)雷诺应力衰减过度,无法依据局部网格分辨率合理演化为RANS 模式,难以产生有效的壁面模化;(2)无法保证流场计算达到正确的LES模式;(3)当雷诺数很高时,网格尺度对于分辨率控制函数的影响将大幅降低,流场计算基本为RANS 模式,无法达到LES 模式。为了克服上述缺陷,Han 等[7-9]提出了一种全新的超大涡模拟理论架构,基于湍流能谱(如图2所示),直接采用3种特征尺度构建分辨率控制函数
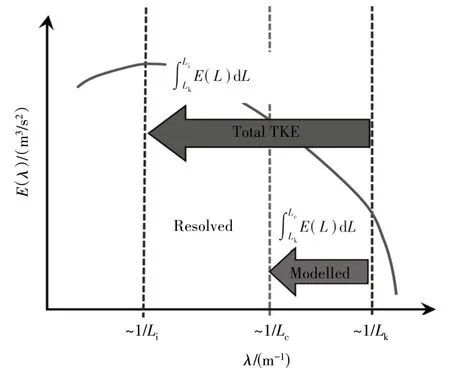
图2 超大涡模拟建模湍流能谱分区
式中:E(L)为长度为L的湍流具有的湍流动能能量密度。
Han等[7-9]通过理论分析和推导,由模化和总体湍动能谱的积分,得到了分辨率控制函数的通用函数形式
式中:β为常数,取值为0.002;Lc、Li和Lk分别为截断网格尺度、积分尺度和Kolmogorov尺度,3个湍流尺度的表达式分别为
式中:Δx、Δy、Δz分别为x、y、z方向的网格尺度;k、ω和β*分别为模化的湍流动能、比耗散率和模型常数,与RANS 中BSLk-ω模型的相应参数一致[7];ν为流体运动黏性;Cx为VLES 中重要的模型参数,是连接VLES和传统大涡模拟LES之间的桥梁。在最初的VLES模型中[9-10],通过引入LES 和RANS 模型常数进行模化,得到模型参数Cx= 0.61。
考虑燃烧室内“受限空间、大分离、强旋流”的流动特点,优化VLES 模型对于复杂物理过程的求解,推导出统一的模型参数模化形式[12],即依据流场参数动态确定模型参数
式中:Cμ为标准k-ε模型参数;Cs为Smagorinsky LES模型参数|为应变率。
可以看出,与原始模型中Cx= 0.61 不同,新模型中Cx随流场变化存在时空演化,可以更加准确地描述湍流的演化过程。
VLES方法实现了对复杂湍流流动的高效高精度数值模拟,在此基础上,进一步耦合燃烧、雾化、污染物、声学等过程的建模,可以实现对燃烧室多物理过程的高精度数值模拟。
需要说明的是,混合RANS/LES 方法存在的一个经典问题是RANS 和LES 模型在模式转换中存在“灰区”现象,在该区域中计算的湍流存在“对数率不匹配”问题[5]。该问题导致从RANS 向LES 的过渡过慢,从而使得对混合过程的计算偏慢。VLES方法极大改进了“灰区”现象,显著优化了“对数率不匹配”问题。尽管如此,在网格非常粗糙的情况下,VLES方法还存在一定的“对数率不匹配”问题,对计算结果的精度有一定影响。
2 燃烧室典型物理过程仿真
2.1 强旋流动超大涡模拟
航空发动机燃烧室通常采用多级旋流、强旋流等流场组织形式[13],旋流流动是燃烧室中最基本的流动形态。由于旋流在流向和切向的流动均占主导,相比传统的管流、槽道流和射流流动等,旋流的湍流脉动具有更强的各项异性,因此旋流的数值仿真对湍流模拟方法提出了很大的挑战。Xia 等[8]采用VLES 方法计算了经典的管内强旋流动算例;Dellenback 等[14]针对该算例开展了流场试验,具有详细的试验数据。计算算例的流动雷诺数为1.0×105(基于圆管直径),旋流数为1.23。计算采用2 套结构化网格,稀疏网格(M1)总数约为90 万,加密网格(M2)总数约为510万,进一步将计算获得的统计矩结果与试验结果进行比较,以验证VLES方法的计算精度。
为了清晰地显示强旋流动下涡旋生成和破碎的演化过程,采用Q 准则等值面来识别旋流场中3 维湍流大尺度结构。由RANS BSLk-ω模型和VLES 模型计算得到的Q 准则等值面识别的湍流大尺度结构的压力分布如图3 所示。从图中可见,传统的RANS 模型只能得到宏观的大尺度结构,无法捕捉到湍流小尺度结构;而VLES 方法能够捕捉到湍流相干结构的瞬态演化过程,即在出口处存在1 个典型的旋进涡核(Precessing Vortex Core,PVC),涡核在进入突扩段后由于剪切K-H 不稳性和流场膨胀导致的压力突变产生剧烈的破碎,由大尺度湍流转变为小尺度湍流。同时,可以发现中心PVC 结构经过破碎后,在下游处的涡旋尺度变小,即涡管直径明显变小。此外,疏密2套网格下VLES 方法计算得到的湍流大尺度结构分布基本一致,区别在于加密网格可以明显地捕捉到更多的涡旋破碎小尺度结构。

图3 Q准则等值面识别的湍流大尺度结构的压力分布[8]
强旋流动下不同下游位置处周向平均速度和脉动速度沿径向分布不同方法计算结果与试验结果的比较如图4 所示。图中横、纵坐标分别为无量纲距离和无量纲速度,其中D1为进口圆管直径,Uin为进口平均速度。从图中可见,流场表现为典型的类Rankin复合涡逐渐向单一刚体涡过渡。比较计算和试验结果,可以发现VLES 方法对强旋流的周向速度预测具有很高的计算精度,与试验测量的分布吻合良好。传统的RANS 方法对旋流计算存在非常大的偏差,无法正确地预测出旋流流场以及湍流脉动的空间演化。相比而言,VLES方法对复杂强旋流动下平均速度场、脉动速度场预测以及空间演化具有非常高的精度,即使在相对稀疏的网格分辨率下依然可以保证较高的计算精度。对于周向平均速度的预测,在疏密2 套网格分辨率下VLES方法的计算结果基本一致。
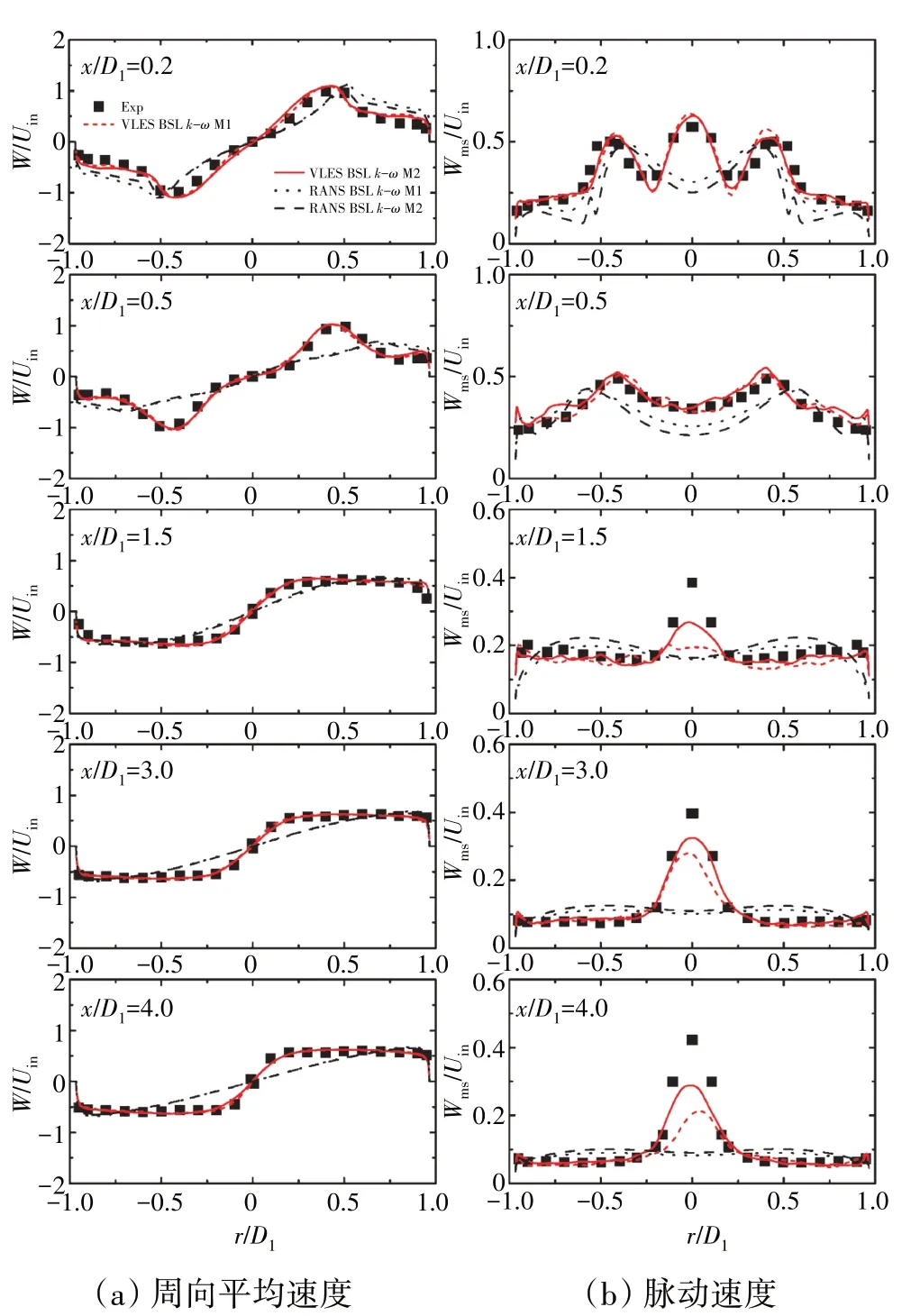
图4 强旋流动下不同下游位置处周向平均速度和脉动速度沿径向分布不同方法计算结果与试验结果的比较[8]
2.2 湍流燃烧超大涡模拟
为了研究VLES 方法预测湍流燃烧问题的可行性[15-16],发展了基于VLES 方法耦合火焰面生成流型建表(Flamelet Generated Manifolds,FGM)[17-18]的湍流燃烧模型,基本思想是假设湍流火焰在局部具有1 维层流火焰结构,湍流火焰面是一系列层流火焰面的系综平均,因此可以将高维组分空间映射到由几个特征变量(混合物分数、反应进度变量等)组成的低维流型,在考虑详细反应机理的条件下,大幅减少了输运方程的求解数量,进而明显降低了计算成本。具体实施过程是基于混合物分数和反应进度变量构建FGM层流数据表,通过假定概率密度函数方法对层流数据表的积分来考虑湍流燃烧间的相互作用,从而获得湍流数据表,数值计算中求解混合物分数、反应进度变量以及相应方差的输运方程,通过查询湍流数据表获得燃烧场信息。
采用VLES 结合FGM 建表的湍流燃烧模型对美国Sandia 试验室试验测量的甲烷/空气湍流射流火焰(Flame D)开展了数值计算,并与试验测量数据进行了定量比较。Sandia Flame D 算例(雷诺数为22400)的燃料物质为体积比1∶3的甲烷与空气完全混合气体,燃料进口速度约为49.9 m/s,伴流速度约为11.4 m/s。值班火焰是已燃的甲烷与空气混合气体,伴流物质是纯空气。计算采用结构化网格,网格总数约为190万。
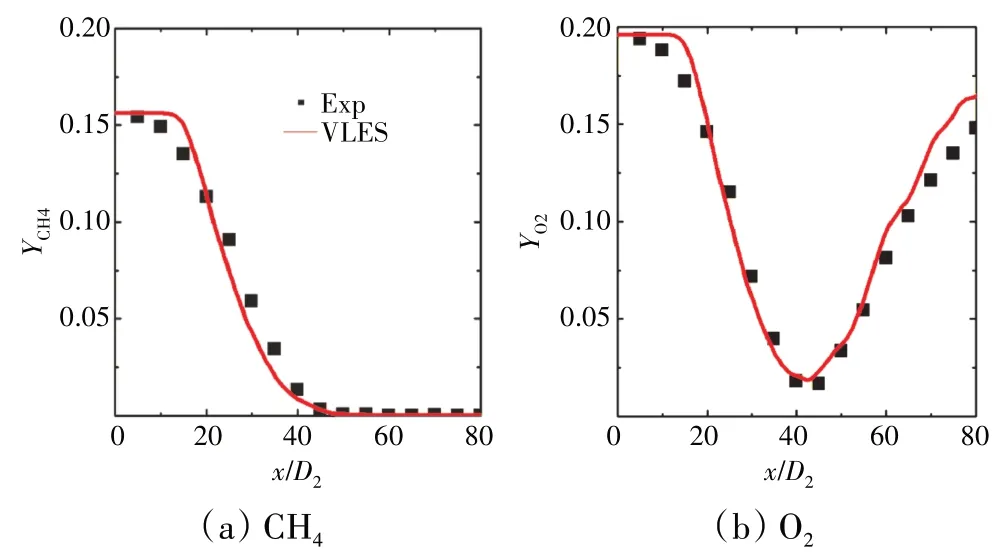
不同组分质量分数平均值沿轴线的分布如图5所示。图中横、纵坐标分别为无量纲距离(D2为进口射流圆管直径)和无量纲质量分数。从图中可见,VLES方法对燃烧过程主要组分的预测与试验结果总体符合良好。不同下游位置处温度在混合物分数空间的散点分布如图6 所示,从图中可见,VLES 方法预测的散点分布趋势与试验结果基本一致,仅计算的温度极值比试验值略高。VLES 计算获得的瞬时涡量、温度和分辨率控制函数分布如图7 所示,其中实线取为Zst=0.351。从图中可见,核心射流区域表现为强湍流脉动,随着流场向下游发展,涡系结构的尺度逐渐变大。从图7(b)、(c)中可见,在绝大部分的化学反应区域,分辨率控制函数处于0和1之间,表明当地网格分辨率可以捕捉到大尺度湍流,仅通过模型模化小尺度湍流,此时VLES 表现为近似大涡模拟求解模式。在射流剪切层和下游的火焰外沿区域,分辨率控制函数接近于1,表明计算网格的截断滤波尺度大于当地的湍流尺度,此时VLES 表现为非定常雷诺平均求解模式。综上所述,可知VLES 方法可以根据涡系结构演化实时特征实现多种湍流求解模式的转变,能够较准确地预测湍流火焰中非定常燃烧过程。

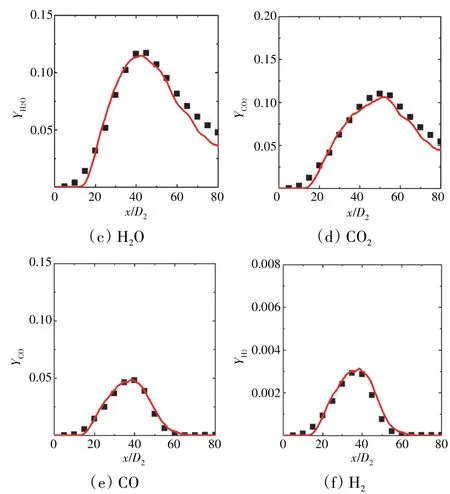
图5 不同组分质量分数平均值沿轴线的分布[15]
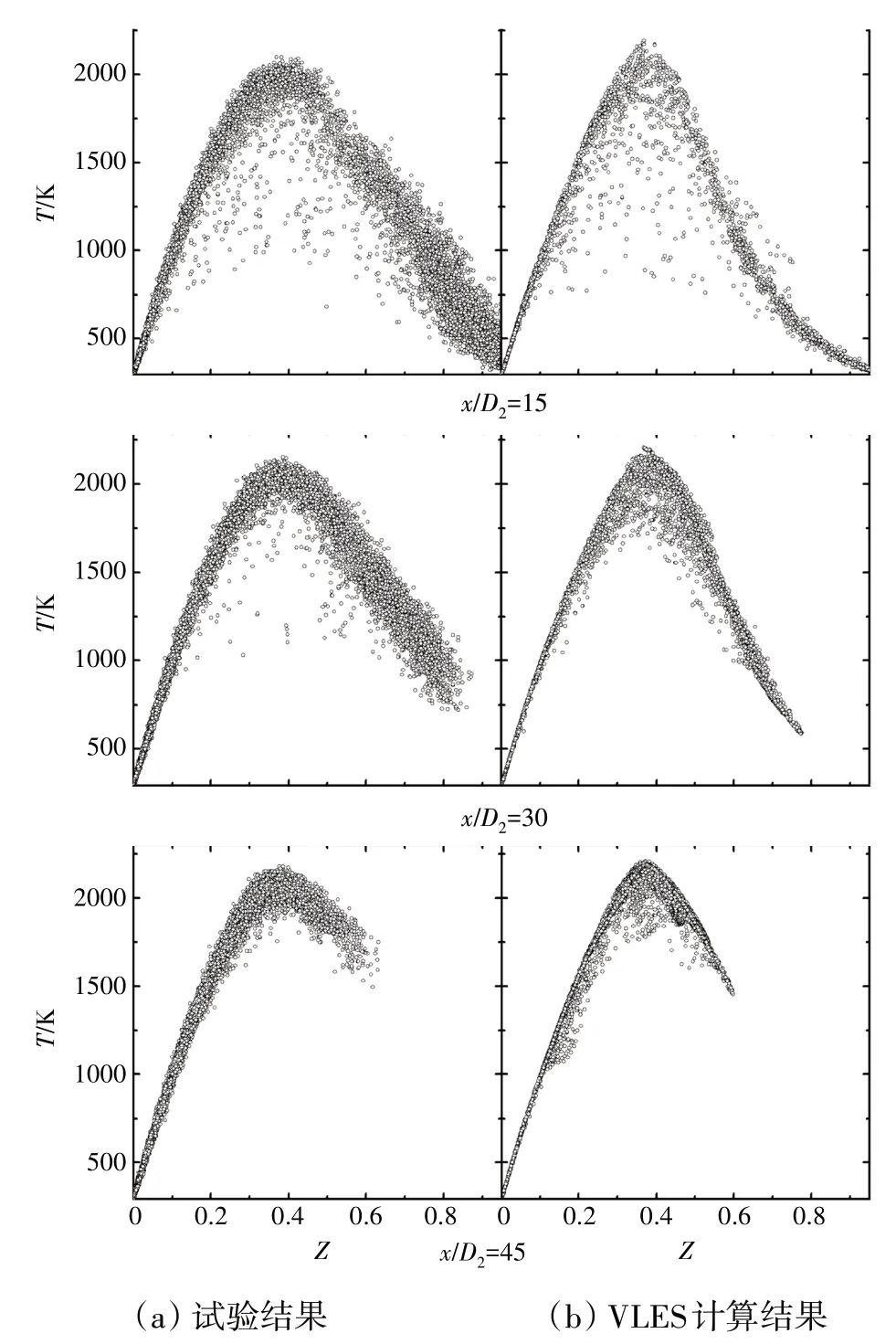
图6 不同下游位置处温度在混合物分数空间的散点分布[15]
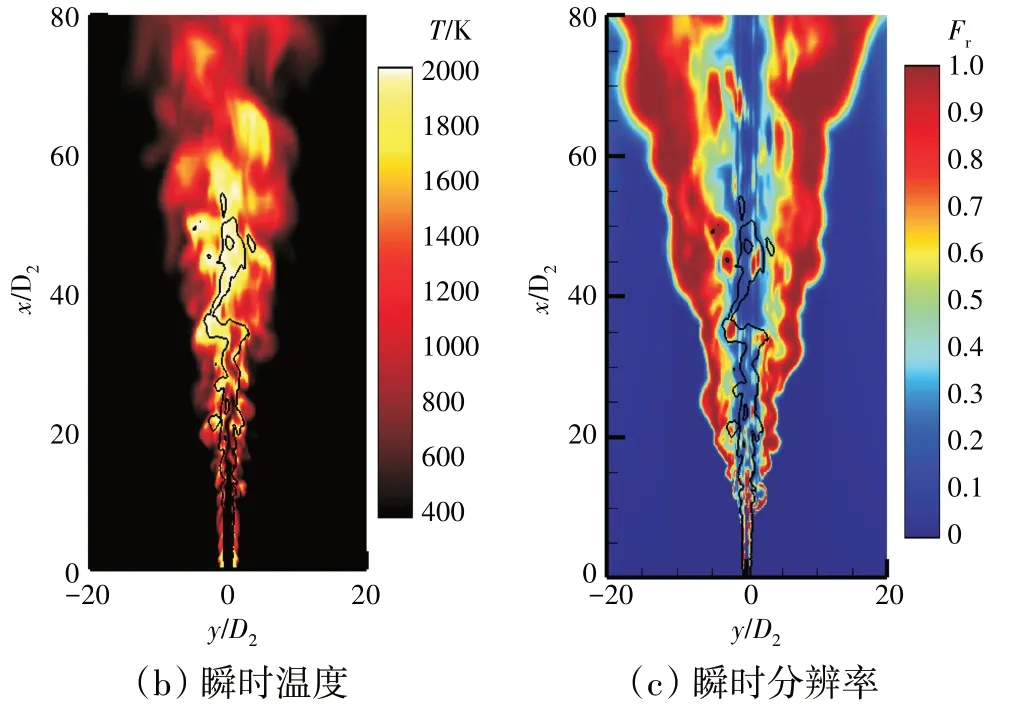
图7 VLES计算的瞬时涡量、温度、分辨率控制函数分布[15]
2.3 完整雾化过程超大涡模拟
航空发动机燃烧室中所用燃料多为液体燃料,液体燃料进入燃烧室经历了一次雾化和二次雾化过程。模拟液体燃料的完整雾化过程面临诸多难点,包括气液两相拓扑界面构型的捕捉、液柱变形和破裂、液带和液丝向液滴的破碎演变、湍流流动和液滴的相互作用等。黄子威[19]发展了基于VLES 方法耦合VOFDPM 混合雾化计算方法的完整雾化过程仿真模型,实现了燃料雾化从连续液体到离散液滴的全流程数值模拟。
采用新发展的雾化过程仿真模型对经典的横向来流下液柱雾化过程开展了高精度数值计算,并与公开文献中的试验结果[20]和大涡模拟计算结果[21]进行了详细比较。计算算例中气相为空气,速度分别为77.89、110.0 m/s,液相为液态水,速度为8.6 m/s,对应的韦伯数分别为100、200。为了更好地模拟二次破碎的过程,破碎模型采用了开尔文-亥姆霍兹和瑞利-泰勒(Kelvin-Helmholtz Rayleigh-Taylor,KHRT)模型。
韦伯数100 工况下VLES 预测的完整雾化过程如图8 所示。从图中可见,在初始区域形成了薄片状液柱,随后液柱破裂成液带和液丝,并在气动力作用下破碎成液滴,液滴通过二次破碎进一步破碎成更小的液滴。韦伯数100工况下VLES 计算的流向速度和展向涡量分布如图9 所示。从图中可见,在液柱的背风侧,存在着典型的低速回流区。通过瞬时涡量分布可以发现,液柱的背风侧表现为强涡旋结构,低速回流区内强湍流运动有助于液柱薄片的破裂和液滴的形成。
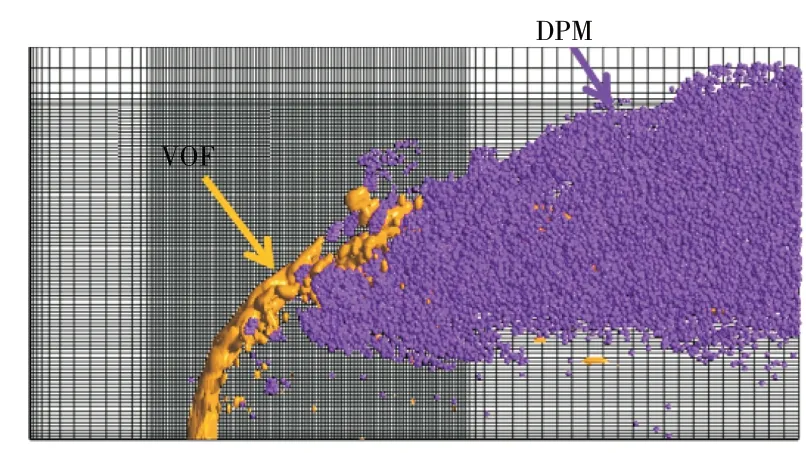
图8 韦伯数100工况下VLES预测的完整雾化过程[19]
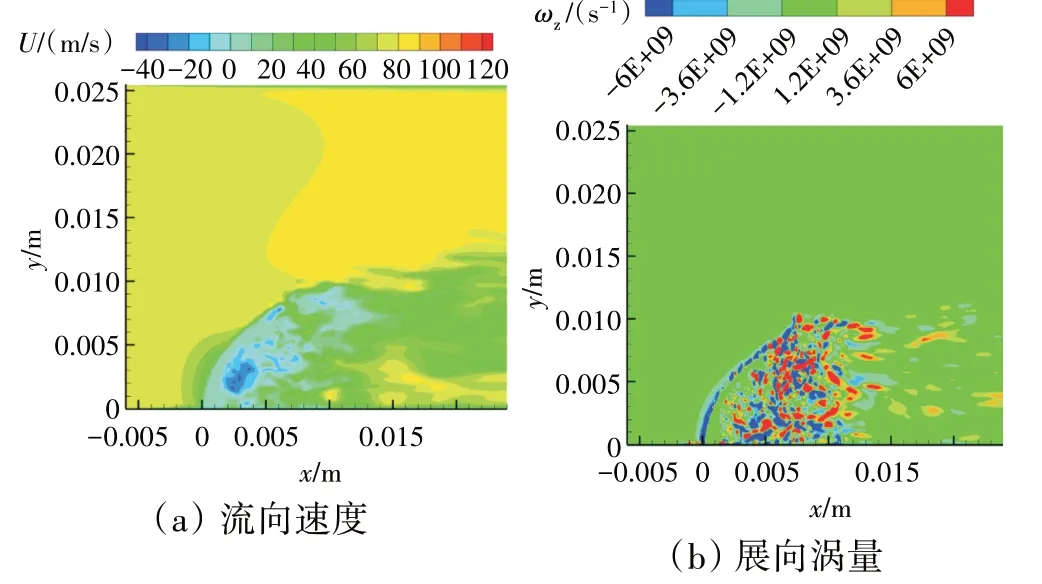
图9 韦伯数100工况下VLES计算的流向速度和展向涡量分布[19]
不同韦伯数下初始射流直径与液柱开始破碎的液体射流最小流向尺寸之比如图10 所示。图中di为液柱开始破碎时液体射流的最小流向尺寸,D3为初始液体射流直径。从图中可见,VLES 计算结果与试验结果吻合良好,优于文献[21]中大涡模拟计算结果。

图10 不同韦伯数下初始射流直径与液柱开始破碎的液体射流最小流向尺寸之比[19]
2.4 碳烟生成超大涡模拟
碳烟(soot)是碳氢燃料燃烧的中间产物,是通过一系列复杂物理化学作用团聚而成的颗粒污染物,碳烟颗粒的排放会形成严重的环境问题。在航空发动机燃烧室中,碳黑的形成会减少可燃烧的碳,从而降低燃烧效率,并且因为辐射换热的增加导致火焰筒壁面温度升高,缩短热端部件的寿命,因此碳烟排放是燃烧室重要的性能评价指标[22]。此外,在典型的湍流火焰中尽管碳烟颗粒的浓度很低,其体积分数多在百万分之一(×10-6)量级,但碳烟的发射辐射却是CO2、H2O等气体发射辐射的2 倍多,因此准确预测碳烟浓度分布对辐射换热以及火焰温度的准确预测极其重要[23]。
碳烟颗粒的形成主要由前驱体形成、颗粒成核、颗粒表面生长和颗粒氧化4 个步骤组成。对碳烟颗粒进行数值计算的模型虽然很多,但是计算精度均难以保证,是目前国际上研究的难点问题。采用基于VLES 方法耦合FGM 建表的湍流燃烧模型对湍流火焰进行数值模拟,结合半经验的碳烟生成模型,即Moss-Brooks 模型[24],利用经验公式求解碳烟成核、表面生长和氧化的速率方程,结合氧化模型和羟基计算模型,初步构建了对碳烟颗粒进行仿真预测的数值模拟方法。
以德国宇航中心试验研究的乙烯/空气湍流射流火焰[25]为对象开展了数值计算,雷诺数为10000,燃烧工况下全局当量比为0.48,火焰可见高度约为400 mm。VLES 计算和试验测量的碳烟颗粒体积分数分布如图11 所示。从图中可见,VLES 计算的碳烟颗粒体积分数峰值约为0.53×10-6,与试验测量值吻合良好,且体积分数的空间分布预测与试验结果也吻合较好。验证结果表明,VLES 方法初步具备了对碳烟颗粒生成的仿真预测能力。
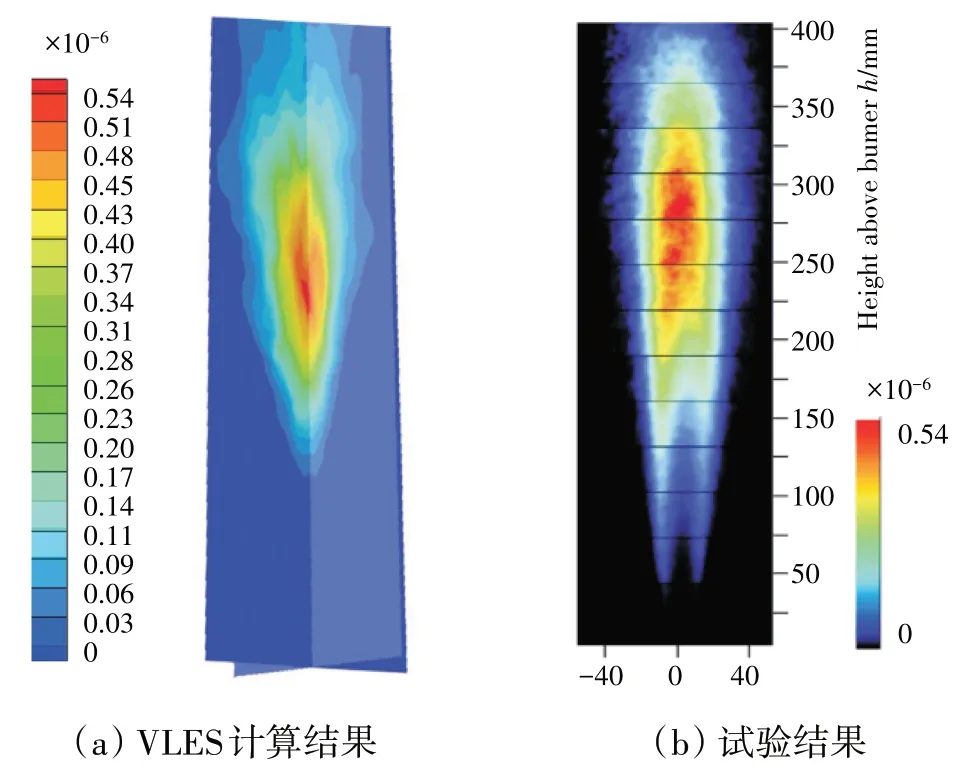
图11 VLES计算和试验测量的碳烟颗粒体积分数分布
2.5 燃烧不稳定超大涡模拟
为了满足低排放要求,民机燃烧室设计通常采用预混或部分预混贫油燃烧组织方式。但是,贫燃预混的燃烧稳定性较差,易于激发热声耦合振荡燃烧模态,导致燃烧不稳定现象的发生。燃烧不稳定具有很强的破坏性,可能伴随有回火、固体变形等问题,是燃烧室设计面临的突出难题。
燃烧不稳定的数值计算可分为解耦方法和直接耦合方法2 大类。解耦的燃烧不稳定预测方法将非定常燃烧和声学求解进行解耦分开。非定常燃烧需要大量的数值计算样本,以构建可靠的火焰描述函数。若采用大涡模拟计算方法,其计算资源消耗过大。直接耦合计算方法是在可压缩求解方式基础上,直接通过高精度的非定常计算获得燃烧不稳定的结果,即在同一个计算框架内一次完成给定工况下非定常燃烧和声学的耦合计算过程[26]。
在燃烧不稳定解耦数值模拟研究方面,Huang等[27]发展了基于VLES方法耦合增厚火焰计算方法的燃烧不稳定计算模型,实现了对声波激励下非定常燃烧过程的准确预测。计算算例为剑桥大学发展的钝体驻定乙烯/空气完全预混火焰,当量比为0.55,雷诺数约为17000。声波激励下非定常火焰动力学特性的VLES 计算结果和试验结果对比如图12 所示。从图中可见,在进口激励过程中,火焰在内外剪切层处翻卷,演化形成反向旋转涡对。在此过程中,蘑菇状火焰轮廓的演变随相位角变化而不断发展。VLES计算结果很好地复现了试验中观测到的火焰演化特性。不同计算方法和试验测量得到的160 Hz 声波激励下热释放率响应振幅和相位差对比如图13 所示。图中Q'、Q͂分别为燃烧的脉动热释放量与平均热释放量,A为正弦声波激励的振幅,图13(b)纵坐标为声波激励下燃烧的瞬态热释放信号与进口速度激励信号之间的相位差。从图中可见,VLES 方法的预测精度与大涡模拟精度[28]相当,均与试验值吻合良好。而非定常RANS 方法虽然预测出了响应非线性的趋势,但是计算得到的定量结果与试验值偏差较大。对于相位差结果(图13(b)),VLES 方法预测的相位差随扰动振幅的变化趋势与试验结果基本一致,而大涡模拟结果[28]并未很好地预测到上述趋势。

图12 声波激励下非定常火焰动力学特性的VLES计算结果和试验结果对比[27](图形左侧为试验结果,右侧为VLES计算结果)
在燃烧不稳定直接耦合数值模拟研究方面,陈涛等[12]发展了基于VLES 方法耦合FGM 建表的燃烧不稳定直接数值模拟方法,通过湍流火焰速度封闭的方法将FGM 建表模型和火焰面密度模型(Flame Surface Density,FSD)进行耦合,可压缩的FGM 建表模型将流体密度和压力利用理想气体状态方程重新耦合求解,从而保证声学波动和燃烧过程二者之间的强耦合。采用发展的燃烧不稳定直接耦合计算方法对经典的LIMOUSINE 燃烧室[29]开展了数值计算研究,该燃烧室由荷兰特温特大学为研究热声耦合燃烧不稳定而设计,为部分预混燃烧室。在算例中,燃烧器上游和下游分别由2 个不同宽度的矩形管道组成,中间由1 个正三角体分隔。上游矩形通道为25 mm×150 mm,计算中上游长度设为80 mm。下游矩形通道为50 mm×150 mm,轴向长度为780 mm。算例中热功率为40 kW,空气系数为1.4。燃料甲烷的质量流量为8×10-4kg/s,空气的流量为0.019152 kg/s。研究表明,VLES方法准确预测了燃烧不稳定的特征频率,同时压力脉动振幅的预测结果也与试验值吻合较好。VLES计算和试验测量的功率谱密度如图14 所示,不稳定周期内温度的演化特性如图15 所示。从图中可见,随着声学特性的振荡,伴随着甲烷在钝体突扩喷口间隙处的反复阻塞流动过程,形成较弱的回火特征。同时,随着声学不稳定周期的循环,新鲜混合物来回往复流动,火焰随之发展或闪回,燃料在中心回流区的反复卷吸过程中,形成了明显的高温涡团结构。
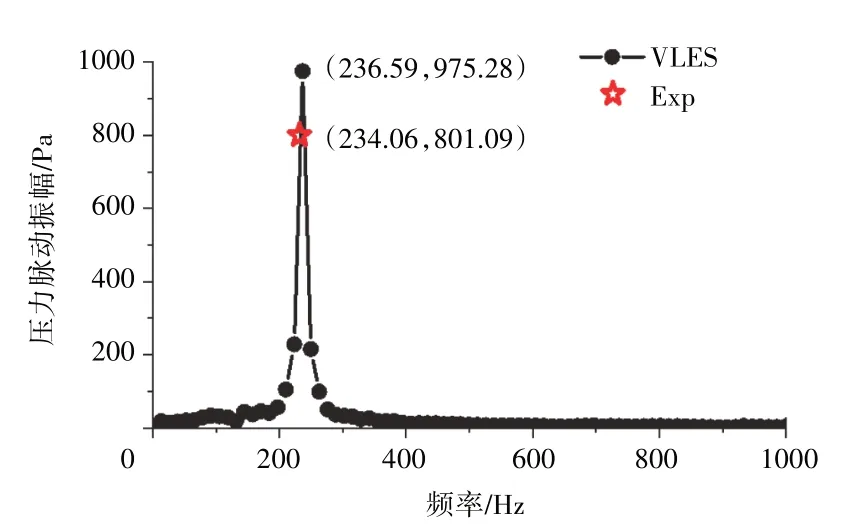
图14 VLES计算和试验测量的功率谱密度[12]
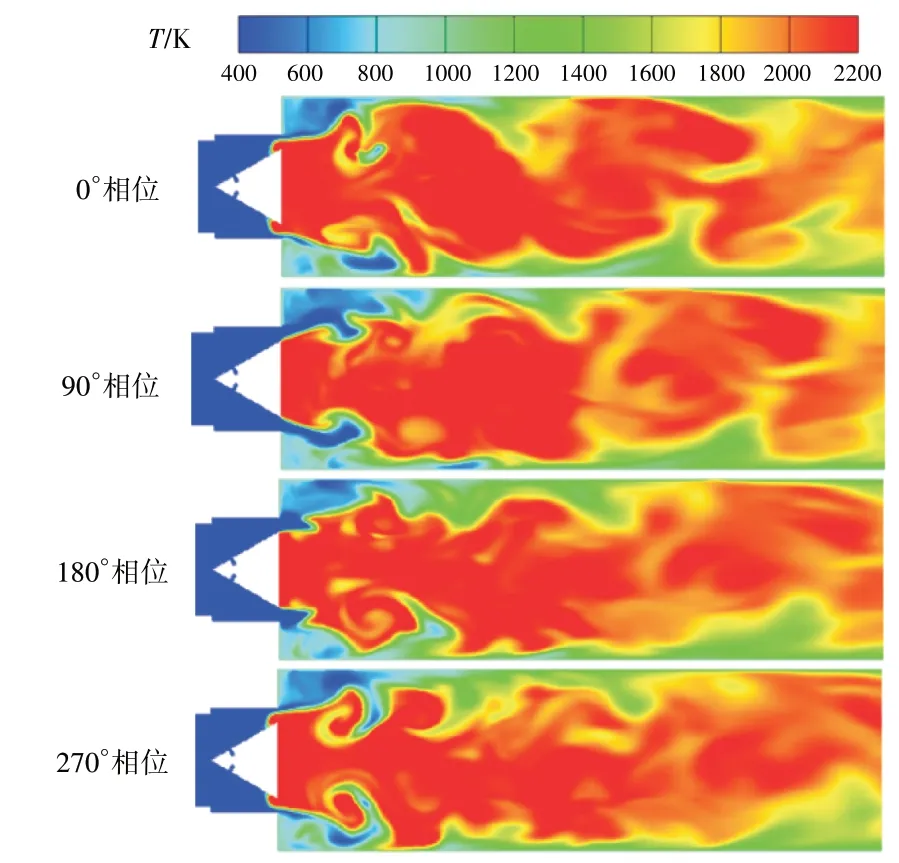
图15 不稳定周期内温度特性分布[12]
3 燃烧室气动性能集成仿真
3.1 GTMC双旋流燃烧室超大涡模拟
选取具有高湍流度的双旋流燃气轮机模型燃烧室(Gas Turbine Model Combustor,GTMC)进行数值仿真研究。国际上基于该模型燃烧室已经开展了大量的试验[30],具有详细的流场和温度场的试验数据。该模型燃烧室主要适用于分析双旋流流动和燃烧的特性以及仿真模型的验证与发展,并已被用作数值仿真的经典验证算例[31-32]。
针对GTMC 双旋流燃烧室,计算选取了试验测量中Flame A 火焰,其中燃料为甲烷气体,空气进口和燃料进口的质量流量分别为19.74、1.256 g/s。当前外旋流器的旋流数为0.9,雷诺数约为58000。计算采用疏密2 套结构化网格,计算网格主要在近壁面和旋流剪切层处进行了加密,稀疏网格(M1)总数约为320万,加密网格(M2)总数约为675万。为了验证不同湍流模拟方法对于受限空间高湍流度旋流燃烧室的计算精度,采用VLES 和传统大涡模拟LES 方法开展了仿真计算,以便相互对比。
GTMC 双旋流燃烧室中不同位置处轴向速度的平均值沿径向的分布如图16 所示。从图中可见,试验测量结果的轴向速度呈现旋流燃烧室中典型的双峰结构,并逐渐向下游扩张衰减。VLES 方法计算得到的轴向速度与试验结果吻合得非常好,可以准确地预测旋流剪切层处的峰值位置及大小。相比而言,LES 方法的计算结果与试验值偏差明显,靠近旋流器出口处预测的轴向速度峰值较试验结果明显偏低,并在下游处双峰快速衰减。进一步分析发现,VLES 和LES 计算得到的内外旋流器旋流数差异较小,而分流比具有明显的差异。VLES计算得到的分流比和试验测量结果较为接近,而LES得到的分流比要明显高于试验值。表明LES 计算得到的外旋流器质量流量相对于实际流量偏高,而内旋流器质量流量则相对偏低。
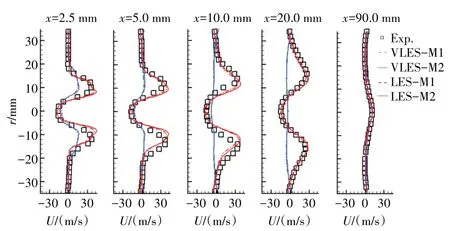
图16 GTMC双旋流燃烧室不同位置处的轴向速度平均值沿径向的分布
GTMC 双旋流燃烧室中不同位置处温度的平均值沿径向的分布如图17 所示。从图中可见,试验测量结果在靠近旋流器出口处温度较低,而在中心处由于存在旋流产生的中心回流区驻定火焰,进而存在温度峰值。此外,两侧由于燃烧室突扩结构形成的外回流区因卷吸一部分高温燃气而温度较高。通过比较平均温度的计算值和试验值可以发现,VLES 方法可以很好地预测不同位置处的温度分布,并较为准确地捕捉温度峰值的大小与位置,与试验结果符合较好。而LES对于温度预测的偏差非常大,由于LES对于集气腔中冲击平板流动以及旋流器中流动预测的累计偏差,导致对于整个旋流场的预测偏差较大,无法正确地捕捉旋流火焰结构。进一步表明LES 方法对于网格分辨率极其敏感,针对复杂燃烧室仿真计算需要极高的计算网格数和计算资源。LES和VLES计算得到的燃烧室瞬时和平均温度分布如图18 所示。GTMC 双旋流燃烧室是典型的旋流气动驻定火焰,从图中可见,火焰悬定在旋流器出口上方,悬定的火焰尖点被称为火焰驻点(Stagnation Point)。通过比较可以发现,靠近旋流出口处,LES 预测的火焰出现明显的壁面附着现象,而VLES 预测的火焰则以一定的角度向下游扩张,呈现典型的V 型火焰拓扑形态。LES 对火焰拓扑形态的错误预测主要是由于网格分辨率不足,引起旋流场的计算偏差。
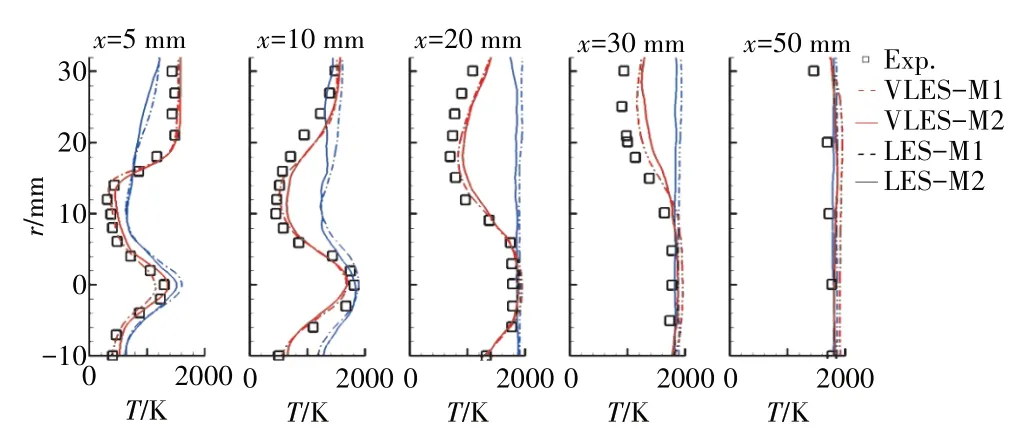
图17 GTMC双旋流燃烧室不同位置处的温度平均值沿径向的分布
3.2 高温升燃烧室超大涡模拟
张宏达[33]等采用VLES方法对高温升燃烧室开展了非定常高精度数值模拟研究,该燃烧室由3 级旋流装置和双油路燃油喷射系统组成,较常规温升燃烧室的流动和燃烧特性更加复杂。计算采用四面体非结构网格,计算网格主要在头部装置和冷却孔处进行了加密,网格总数约为1500 万。选取高温升、高热负荷工况作为燃烧室数值模拟的工况点,关于数值方法的详细介绍见文献[33-34]。
高温升燃烧室中心截面瞬时和统计平均速度分布VLES 计算结果如图19 所示。为了表征回流区的形状,用零速度等值线表示(图中黑线)。从图中可见,气流在燃烧室扩压器内减速后,经头部旋流装置形成旋流,进而生成中心气动回流区a,中心回流区用于驻定火焰和小工况稳定燃烧;同时火焰筒壁面和第3 级旋流气体之间、以及第2 级旋流和第3 级旋流气体之间分别形成了突扩回流区b 和c。主燃孔和掺混孔的多股射流与火焰筒内横向来流相互作用,形成了反向旋转涡对,进一步强化了湍流输运和混合。
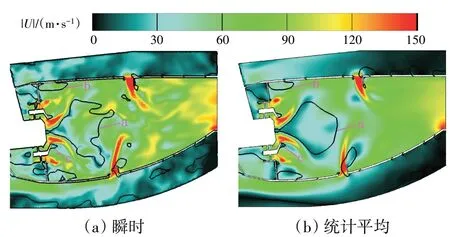
图19 高温升燃烧室中心截面瞬时和统计平均速度分布VLES计算结果[33]
高温升燃烧室中心截面的瞬时温度场和统计平均温度场VLES 计算结果如图20所示。从图中可见,气流经过头部旋流装置形成的大尺寸中心气动回流区,一方面由于强湍流运动促进了液体燃料雾化蒸发,另一方面燃料气体与来流空气在中心回流区内混合燃烧,导致温度快速升高,是火焰筒内温度最高的区域。大孔射流用于强化高温燃气与射流空气间的掺混,调控获得满足设计要求的出口温度场。高温升燃烧室出口径向温度分布曲线如图21 所示。通过比较计算结果和试验结果可以发现,由于传统RANS 方法不能正确捕捉燃烧室中强旋流和非定常火焰结构,导致出口温度分布的预测偏差非常大。而VLES 方法的预测结果与试验结果较为接近,较准确地捕捉了出口径向温度分布的峰值位置。VLES计算结果与试验结果的偏差体现在火焰筒出口截面径向相对位置60%以下,分析认为物理建模中未考虑实际的火焰筒冷却结构,可能导致火焰筒出口近壁气膜与高温燃气间的混合程度不足,从而引起计算偏差。
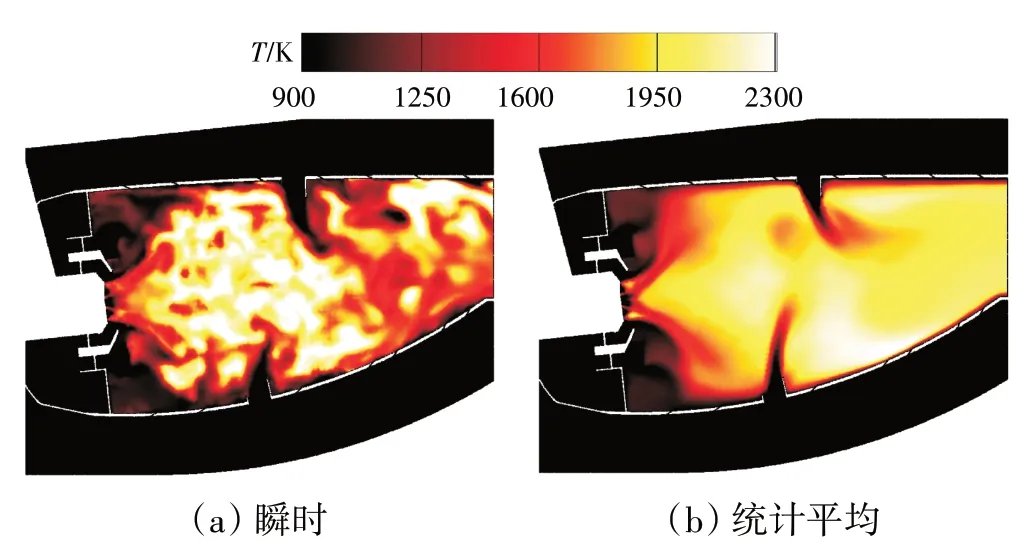
图20 高温升燃烧室中心截面瞬时和统计平均温度场VLES计算结果[33]

图21 高温升燃烧室出口径向温度分布[33]
4 总结
(1)针对燃烧室内多尺度强耦合物理化学过程,介绍了高精度建模和数值模拟面临的技术挑战,对超大涡模拟的基本思想和模型理论进行了阐述,实现了从实验室尺度到复杂工程应用场景下湍流流动与燃烧的高精度、高效率的数值模拟。
(2)根据超大涡模拟理论架构,发展了VLES 耦合FGM 建表的湍流燃烧模型、VLES 耦合VOF-DPM雾化计算的完整雾化过程仿真模型、VLES 结合碳烟生成预测模型、燃烧不稳定解耦和直接耦合数值计算模型,实现了燃烧室中旋流流动、燃烧、雾化、碳烟生成和燃烧不稳定等典型多物理过程的高精度仿真预测。
(3)选取双旋流模型燃烧室和高温升燃烧室,开展了基于超大涡模拟的气动性能集成仿真研究,为方案筛选、设计优化和性能评估提供了工程可用的3 维非定常仿真手段,有望在实际航空发动机燃烧室设计中规模化应用。
