翼型水下航行器的控制系统设计*

戴敬轩 ，高 洁 ，熊囿铭

（南通理工学院电气与能源工程学院，江苏 南通 226002）

海洋牧场建设是改变海洋渔业发展模式的重要探索，也是促进海洋经济发展和海洋生态文明建设的重要举措。要实现海洋牧场建设，对海洋信息的探索与收集成为海洋经济活动中的重中之重[1]。水下航行器的出现与应用能克服水下观测中无氧、压力、水温等不利因素对水下工作的影响。本文设计的翼型水下航行器则从仿生学的角度，进一步优化了传统水下航行器中普遍存在的体积大、能耗高、灵活度低的问题，在大大缩减水下航行器成本的同时还提高了其灵活性。

1 翼型水下航行器的运动建模

1.1 坐标系建立

想要构建翼型水下航行器的运动模型，首先需明确其在三维空间中的运动情况及运行环境。将此翼型水下航行器的运动控制分为六个自由度方向上的运动，分别为：纵荡（轴向运动）、横荡（横向运动）、垂荡（垂向运动）、横摇（横倾运动）、纵摇（纵倾运动）与艏摇（偏航运动）。并将其当作一个典型刚体建立水下航行器体笛卡尔坐标系{b}[2-4]。同时，为研究其在水下环境中的位置与运行状态，特使用z轴垂直指向地心的地固坐标系{n}与水下航行器体笛卡尔坐标系{b}组成参考系，如图1所示，方便采用牛顿第二定律来对其进行运动分析。

图1 地固坐标系与水下航行器体笛卡尔坐标系

1.2 建立运动方程

由欧拉旋转定理可知，两刚体或坐标系{A}与{B}之间相对的方位每一次变化都可以用{B}在{A}中的旋转来描述。通过描述其相互转换的中间表达式，可以更方便地将水下航行器的运动状态描述出来并建立运动方程。在描述水下航行器姿态信息时，可使用动坐标系原点O在静坐标系上的坐标值和动坐标系相对于静坐标系的三个姿态角：ϕ（横摇角）、θ（纵摇角）与ψ（艏摇角）来表示[3-4]。

在翼型水下航行器的运动描述中，均使用国际通用的SNAME（海军建筑师和船舶工程师协会）符号，如表1所示。

表1 SNAME符号表

在翼型水下航行器的运动分析中，其数学方程是在动坐标系中建立的，假设水下航行器体笛卡尔坐标系{b}与地固坐标系{n}的原点重合，那么可以利用线性变换将其表示出来。设一线性变换矩阵P，水下航行器体笛卡尔坐标系{b}与地固坐标系{n}的转换矩阵表达式为POE，而PEO为POE相反的转换矩阵表达式[5]。两矩阵可以分别表示为：

对其进行反变换可得：

使用表1中六个参数对其在三维空间中的运动进行描述，则静坐标系下的参数为而动坐标系下的参数为[u v w p q r]，经推导可得翼型水下航行器的三维空间六自由度运动方程为[6-8]：

2 翼型水下航行器的控制系统分析

2.1 系统概况

本文所研究的水下航行器巧妙利用了仿生学原理，模拟蝠鲼设计了一款流线型AUV，并设置了两个在后方的水平推进器以及两个藏于两翼的垂直推进器，航行器三维设计图如图2所示。这样的设计可以有效地减少水下航行器在水中的运动阻力，同时构成了一个欠驱动系统，在节约能量、降低造价、减轻重量、增强系统灵活度等方面都优于传统的完全驱动系统。

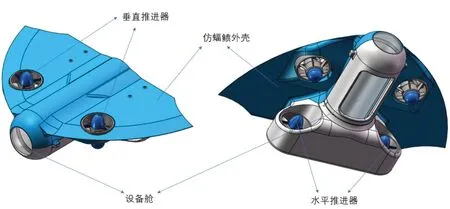
图2 翼型水下航行器三维设计图

2.2 控制系统流程图

该系统是以四个电机控制六自由度的欠驱动系统，只以四个推进力来完成六种运动方式。本文针对水下航行器这一类型的欠驱动系统制作了控制流程图，如图3所示。图中所贯彻的控制思想是将控制量经过控制方程的处理作用于运动方程，实现运动控制，并不断通过参数反馈对控制量进行调整，形成闭环控制。其中，控制算法的设计与实现尤为重要。

图3 翼型水下航行器的控制流程图

3 翼型水下航行器控制算法设计

控制系统选用比例积分微分控制，比例积分微分控制（PID）是最早发展的控制策略之一，同时也是目前商用水下航行器最常用的位姿控制技术，算法简单、鲁棒性好以及可靠性高是它的优势所在。其控制原理如图4所示，通过调节比例增益Kp、积分增益Ki与微分增益Kd来控制系统达到稳态[9-10]。

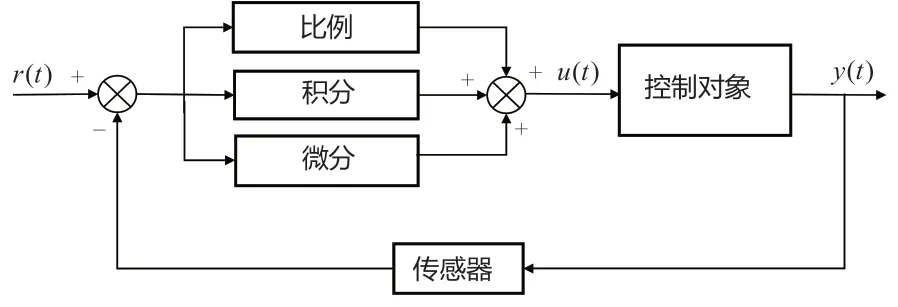
图4 PID控制原理图

PID的控制输入信号为：

式中，Kp为比例增益参数，Ki为积分增益参数，Kd为微分增益参数，三个参数均为非负数。

传递函数是将系统模型从时域转换到频域的有效工具，而频域是控制系统工作所必需的。PID控制系统的传递函数由PID控制器传递函数和被控对象的传递函数两部分组成，其中，PID控制器的传递函数为：

整个PID控制系统的传递函数可以表示为：

所以，本设计的翼型水下航行器的控制系统中采用PID控制算法，并在传统PID算法的基础上进行优化，利用离散化方法将连续时间t用采样时刻点KT代替，以矩形法数值积分近似代替积分，以差分近似代替微分，得到离散PID控制的表达式[10]，即：

4 实验分析

为了验证控制系统设计的可行性，对翼型水下航行器进行了水池实验，如图5所示。

图5 水池实验

对艏摇运动在水下环境中的实验结果进行分析，如图6所示。图中的艏摇阶跃响应，即ψ，在10 s时由2 rad旋转至4.8 rad。其中，5 s~10 s之间的波动是由于水池较小，系统受到了回波影响，可忽略，主要看调节器的反应速度。图中的黑色线条为理想参考，红色线条为PID调节之后的阶跃响应，不难看出PID控制器的阶跃响应能够实现较快速的收敛，大约需要8 s，基本达到了设计要求。

图6 艏摇水下环境中PID控制器实验结果图

5 结语

本文对某翼型水下航行器进行了控制系统设计，在设计过程中，首先建立了动静坐标系，求出了水下航行器的空间运动方程；其次针对欠驱动系统进行了船体分析并制作了控制系统结构图，根据控制需要选用了PID控制算法并进行了适当优化；最后对其进行了实验分析，验证了此控制系统的可行性，以期为后续的翼型水下航行器控制系统的设计提供参考。