不同损伤模型下超高性能混凝土SHPB试验数值模拟对比

2023-09-13郑胜佩蔡昂霖郭忠照喻贤明

沈阳建筑大学学报（自然科学版） 2023年4期

任亮,郑胜佩,蔡昂霖,郭忠照,喻贤明

(1.华东交通大学土木建筑学院,江西南昌 330013;2.华东交通大学土木工程国家实验教学示范中心,江西南昌 330013;3.南昌中铁穗城轨道交通建设运营有限公司,江西南昌 330013)

超高性能混凝土(UHPC)是一种粗骨料细化、加入高性能外加剂、以硅灰和其他超细矿物作为掺合料的新型水泥基复合材料,具有优异的力学性能和耐久性能,以短节纤维作为增强和增韧材料,使其又具备其他混凝土不具备的良好韧性[1]。为适应UHPC结构在冲击或爆炸等极端荷载下的需求,对UHPC材料开展冲击试验是探讨其动态力学性能的重要途径。由于分离式霍普金森压杆(Split Hopkinson Pressure Bar,SHPB)试验可以覆盖结构大部分爆炸和冲击的应变率范围,不少学者应用SHPB技术对UHPC冲击性能开展了研究,结果表明,UHPC试件在冲击作用下存在显著的应变率效应[2],峰值应力、峰值应变、弹性模量以及耗能能力随应变率的增加而增大[3],UHPC材料表现出良好的抗冲击性能[4]。但考虑到UHPC材料动力特性影响因素较多,而试验研究通常成本高、耗时长、数据离散性大,为此开展数值模拟研究是对其重要的补充。

LS-DYNA软件作为一种大型非线性有限元程序,为用户提供了十余种混凝土损伤模型,其中*MAT_72R3、*MAT_111和*MAT_159模型因其能较好地反映混凝土材料在冲击荷载下的应变率效应、软化、失效、损伤演化等动态性能,而被广泛应用于模拟混凝土材料的冲击性能[5]。针对UHPC材料,任亮等[6]基于校准的Karagozian-Case-Concrete(KCC)冲击损伤模型,探讨了SHPB试验中径向惯性效应对UHPC试件应力平衡的影响,给出了高应变率下UHPC试件长径比的合理取值范围。徐世烺等[7]基于校准的Holmquist-Johnson-Cook(HJC)冲击损伤模型指出,随着应变率增加,UHPC材料的动态应力-应变曲线呈现出由应变硬化主导向损伤软化主导的转变趋势。任亮等[8]结合UHPC的材料特性,校准了HJC模型中关键参数的取值,探讨了强度参数A与参考应变率之间的相关性。W.Guo等[9]基于UHPC单轴和三轴压缩试验数据,校准了Continuous-Surface-Cap(CSC)冲击损伤模型中关键参数的取值,分析了UHPC梁在低速落锤冲击下的动力性能。贾鹏程等[10]进一步指出CSC模型对UHPC梁出现的剪胀效应描述较差。

虽然应用上述三种损伤模型目前已实现了对UHPC动力冲击特性的数值研究,但考虑到三种损伤模型在不同冲击应变率下反映材料复杂应力行为的差异性,导致模拟效果不尽相同,而现有的研究针对UHPC材料在三种损伤模型下的动态力学行为对比鲜有文献涉及。基于此,笔者应用大型有限元程序LS-DYNA,结合UHPC材料特性,明确KCC、HJC和CSC模型中关键参数的取值,建立超高性能混凝土SHPB试验数值仿真模型。在此基础上,将不同损伤模型下UHPC试件波形、动态应力-应变曲线、弹性模量和DIF值模拟结果与实测结果进行对比,探讨不同损伤模型下超高性能混凝土SHPB试验动态破坏进程。

1 基于UHPC材料的损伤模型参数确定

1.1 KCC模型参数确定

KCC模型通过定义三个独立的剪切破坏面来控制混凝土类材料处理复杂应力条件下的非线性行为[11],应用线性插值函数考虑当前应力状态的损伤累积。其中剪切破坏面由参数a0y、a1y、a2y、a0、a1、a2、a1f、a2f来确定,三个剪切破坏面之间的应力通过损伤函数η和等效塑性应变λ来确定。为准确描述混凝土材料模型的压缩行为,KCC模型通过体积应变εv、静水压力P和卸载体积模量K来确定状态方程。笔者在文献[6]中基于UHPC材料特性,结合KCC模型的特点,明确了上述控制参数的取值,结果见表1和表2。

表1 KCC模型剪切破坏面参数Table 1 Parameters of the shear failure surface in KCC model

表2 KCC模型损伤方程、状态方程参数Table 2 Parameters of the damage function and equation of state in KCC model

1.2 HJC模型参数确定

HJC模型作为一种与应变率相关的材料损伤模型,其本构关系通过损伤函数和静水压力-体积应变关系来确定[12],模型中相应的控制参数包括基本参数、损伤参数、压力参数和强度参数。

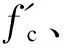
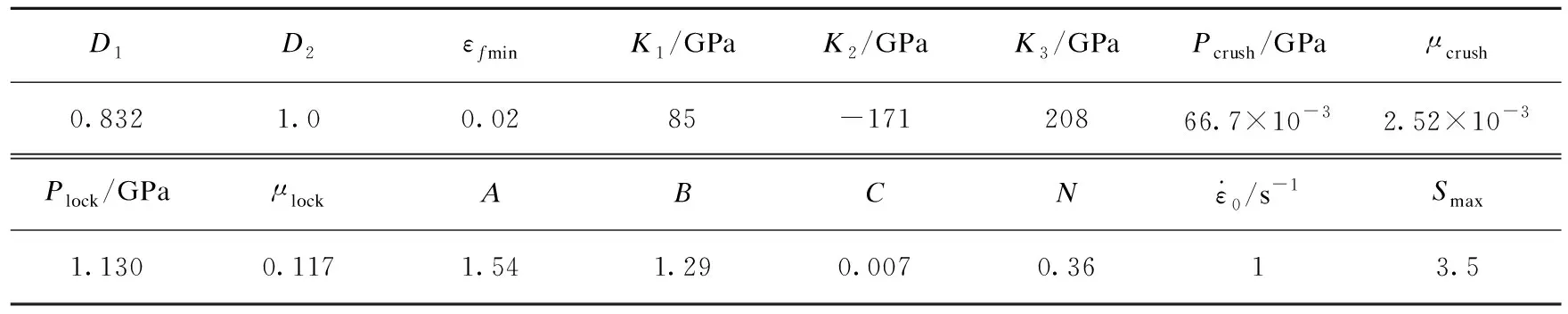
表3 HJC模型损伤参数、压力参数和强度参数Table 3 Parameters of the damage,pressure and strength in HJC model

1.3 CSC模型参数确定

CSC模型通过屈服面方程(包含剪切破坏面方程和盖帽硬化面方程)、损伤方程以及应变率效应方程来表征混凝土材料的硬化、损伤及应变率效应[13]。其中剪切破坏面由压缩子午线(参数α、β、λ、θ)、剪切子午线(参数α1、β1、λ1、θ1)和拉伸子午线(参数α2、β2、λ2、θ2)共同确定;盖帽硬化面方程参数包含了盖帽初始位置X0、最大塑性应变W、线性形状参数D1、二次形状参数D2和盖帽面长轴与短轴的比值n;损伤方程参数包含了塑性形状软化参数B、单轴受压断裂能Gfc、脆性形状软化参数D、单轴受拉断裂能Gft、纯剪断裂能Gfs、剪压转换参数PWRC、剪拉转换参数PWRT和自定义软化参数PWRD;应变率效应方程参数包含了单轴受压应变率效应参数η0c、单轴受压应变率效应功率Nc、单轴受拉应变率效应参数η0t、单轴受拉应变率效应功率Nt、受压最大允许过应力OVERC、受拉最大允许过应力OVERT、有效剪应力与拉应力流动参数的比值SRATE和通过应变率效应增加断裂能的功率REPOW。

表4 CSC模型参数Table 4 Parameters in CSC model(UHPC)

21.78 .

(1)

(2)

18.8.

(3)

(4)

(5)

104.87.

(6)

2 冲击压缩数值仿真模型

应用大型有限元程序LS-DYNA,分别选用文献[14-16]中不同应变率下超高性能混凝土SHPB试验,建立冲击压缩数值仿真模型。三组文献中整形器均采用铜质,相应的材料参数见表5。其中文献[14]中整形器材料直径和厚度分别为20 mm和2.5 mm,UHPC试件直径和长度分别为56 mm和26 mm,相应的单轴抗压强度为165 MPa,应变率为60 s-1;文献[15]中整形器直径和厚度分别为10 mm和2 mm,UHPC试件直径和长度分别为23.8 mm和9.2 mm,相应的单轴抗压强度为200 MPa,应变率为92.03 s-1;文献[16]中整形器直径和厚度分别为6 mm和1 mm,UHPC试件直径和长度分别为36 mm和17.5 mm,相应的单轴抗压强度为125 MPa,应变率为166 s-1。

表5 波形整形器材料参数Table 5 Material parameters of pulse shaper

各杆件的特征参数见表6。其中文献[14]中的入射杆为全长3 200 mm的直锥变截面杆,靠近撞击杆端为长50 mm、直径37 mm的等直径段,之后采用长400 mm、直径由37 mm渐变为74 mm的过渡段,再采用直径74 mm的等直径杆;文献[15]和文献[16]中分别采用直径为25.4 mm和40 mm的等截面杆。

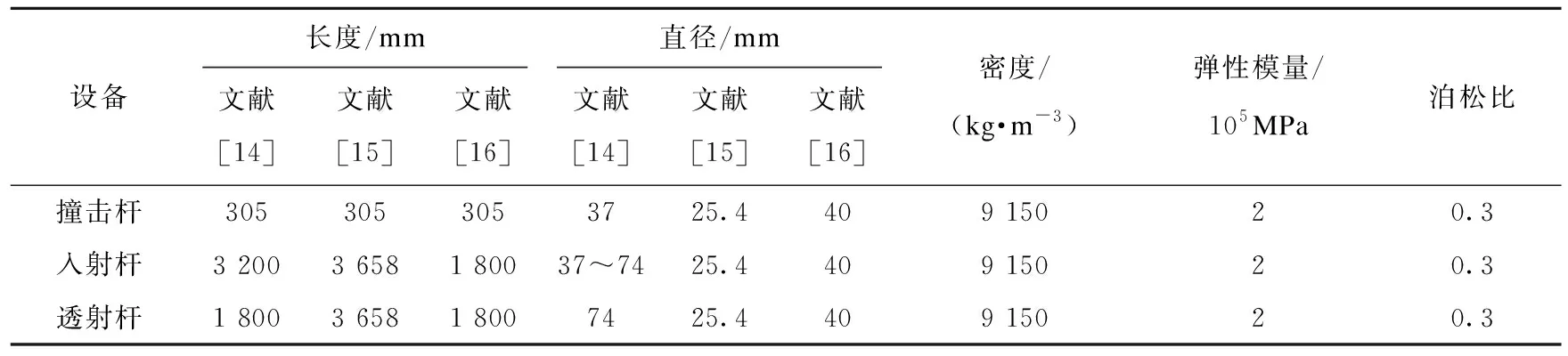
表6 杆件特征参数Table 6 Characteristic parameters of the bars

SHPB数值仿真模型示意图如图1所示。模型中各构件均采用solid164实体单元,为降低负体积的影响,在杆件与试件、杆件与整形器接触部分的单元进行适当网格细分,具体网格划分见表7。为消除端面摩擦效应的影响,各构件之间端面接触均采用自动面面接触。为准确模拟冲击过程中大变形构件动态弹塑性力学行为,选用Plastic-Kinematic模型作为整形器的材料模型,选用前述参数校准后的KCC、HJC、CSC模型分别作为UHPC试件的动态损伤模型。

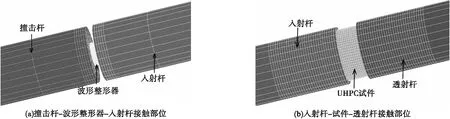
图1 SHPB数值仿真模型Fig.1 Numerical simulation model of SHPB

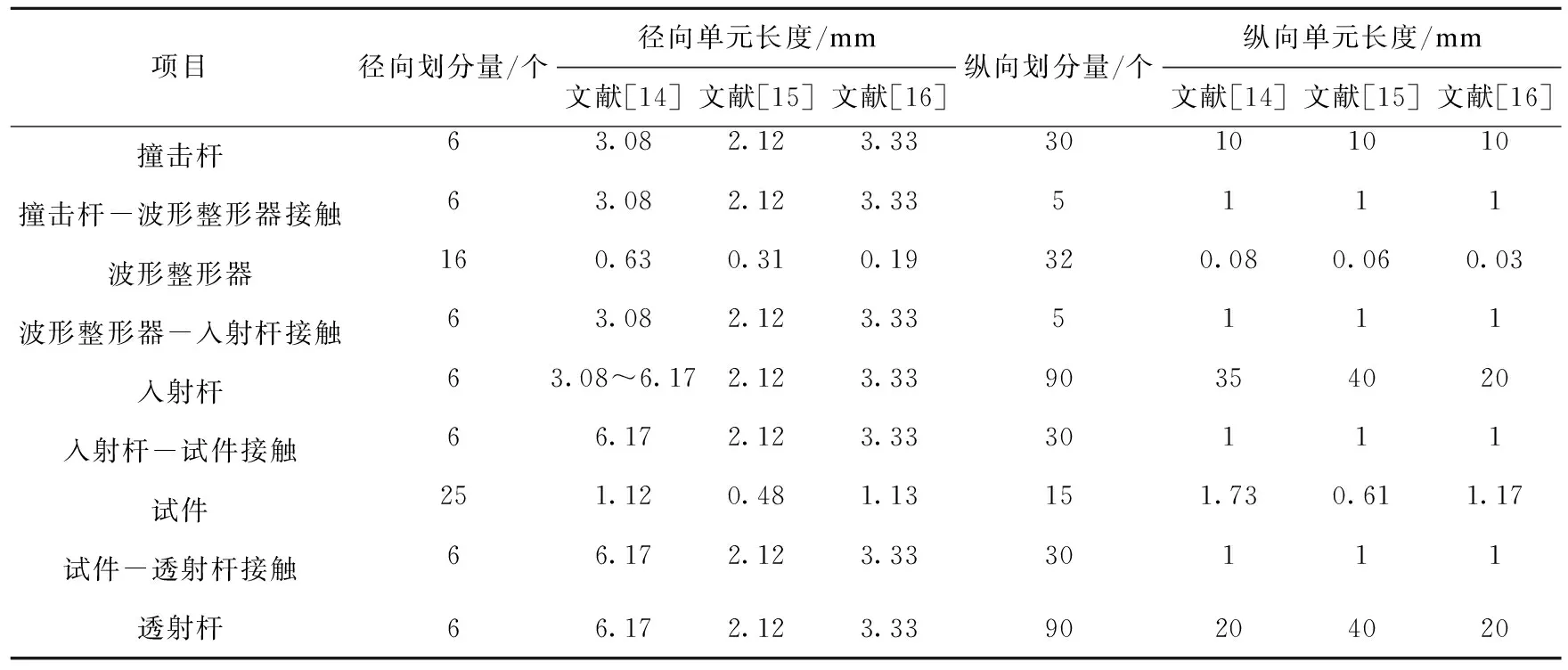
表7 模型网格划分Table 7 Model meshing

3 损伤模型模拟结果对比

基于上述数值分析方法,分别选用校准后的KCC模型、HJC模型和CSC模型,对文献[14-16]中SHPB试验开展数值仿真分析。

3.1 波形对比

不同损伤模型下实测波形和计算波形的对比如图2所示。从图中可以看出,在低应变率时(60 s-1),相对于KCC模型和HJC模型,CSC模型得到的计算波形与实测波形吻合度更高,表明CSC模型在低速冲击下具有更好的模拟效果。此后随着应变率的提高,CSC模型得到的透射波下降段和反射波上升段相对于实测波形表现出一定偏差,且这种偏差在应变率达到166s-1时显著增大;而KCC模型和HJC模型在中高应变率下计算波形与实测波形保持较好的吻合度。这是由于CSC模型通过盖帽面的膨胀和收缩来模拟材料的塑性变形,考虑到中高应变率下UHPC试件产生较大的变形,盖帽面的膨胀和收缩不足难以描述UHPC试件的塑性变形,导致试件部分单元提前出现失效,大大影响了计算结果的准确性;而KCC模型和HJC模型分别通过剪切破坏面和塑性体积应变的累积来控制材料的损伤行为,能更好地描述UHPC材料内部孔隙压实以及纤维的桥接效应,进而取得较好的模拟效果。

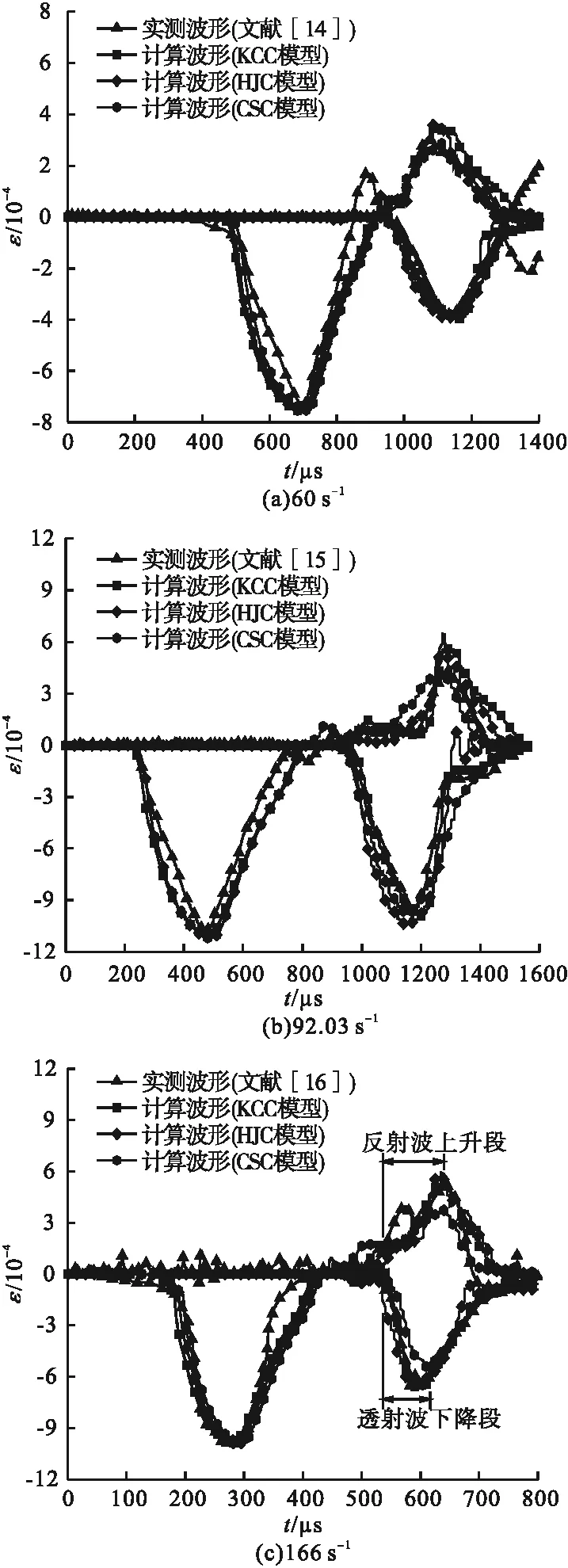
图2 实测波形与计算波形对比Fig.2 Comparison of the measured and calculated aveforms

3.2 动态应力-应变曲线对比

为进一步探讨不同损伤模型下UHPC材料在冲击作用下的应变硬化和损伤软化特征,图3给出了不同损伤模型下动态应力-应变曲线。从图中可以看出,在低应变率时(60 s-1),由CSC模型得到的计算曲线上升段和下降段与实测曲线吻合度优于另外两种模型,表明基于路边钢筋混凝土防护结构与车辆碰撞而开发的CSC模型对低速冲击具备更好的适用性。随着应变率提高,HJC模型和KCC模型得到的计算曲线与实测曲线吻合度逐渐提升,而CSC模型得到的计算曲线与实测曲线逐渐偏离,且损伤软化段出现快速下降,这是由于中高应变率下UHPC试件将产生较大的变形,CSC模型中盖帽面的膨胀和收缩不足使试件部分单元提前失效所致。

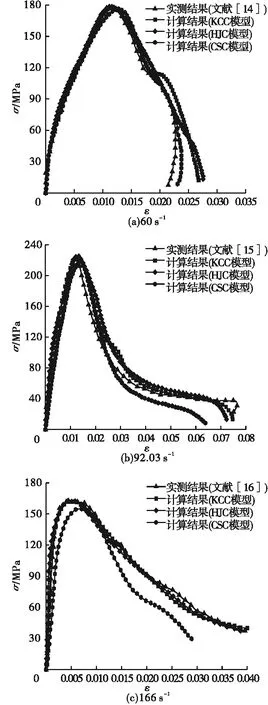
图3 UHPC动态应力-应变曲线实测结果与计算结果对比Fig.3 Comparison on the dynamic stress-strain curves between the measured and simulated results for UHPC

为进一步探讨KCC模型、HJC模型和CSC模型模拟效果的差异性,图4和图5分别给出了不同损伤模型下UHPC弹性模量和DIF实测值与计算值对比,其中弹性模量定义为图3中上升段0.4倍峰值应力对应的割线弹性模量[17-18]。

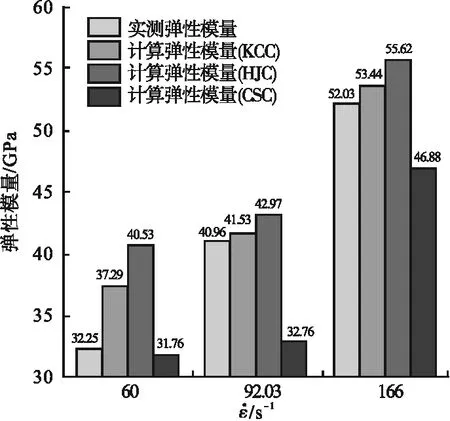
图4 不同损伤模型下UHPC的弹性模量实测值与计算值对比Fig.4 Comparison on the elastic modulus between the measured and simulated results for UHPC under different damage models

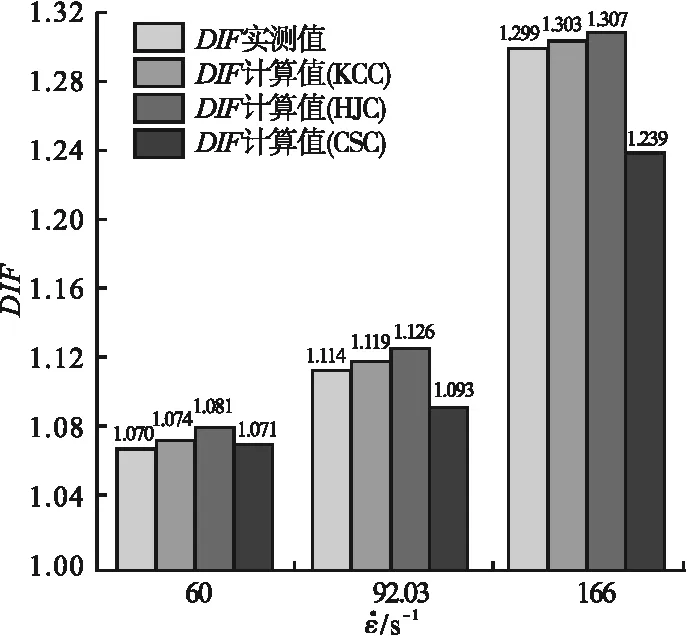
图5 不同损伤模型下UHPC的DIF值实测值与计算值对比Fig.5 Comparison on the DIF values between the measured and simulated results for UHPC under different damage models

从图4中可以看出,三种损伤模型模拟得到的结果从大到小依次为HJC弹性模量值、KCC弹性模量值、CSC弹性模量值,且在低应变率下CSC模型弹性模量计算值与实测值偏差最小;但随着应变率提高,CSC模型弹性模量模型计算值与实测值偏差逐渐差逐渐减小,这与前述三种模型下波形曲线和动态应力-应变曲线对比表现一致。在中高应变率下,相对于HJC模型,KCC弹性模量模型计算值与实测值更吻合,这是由于KCC模型基于状态方程解耦体积变形响应和剪切响应来描述材料的压缩行为,能更为真实地反映出UHPC材料的内部损伤。而HJC模型中静水压力-体积应变状态方程由线弹性段、塑性应变阶段和完全压实阶段组成,导致UHPC材料内部空隙没有足够的时间实现完全压实,只能通过增强试件动态损伤能力(如弹性模量、动态抗压强度)的方式来实现能量平衡。

从图5可以看出,三种损伤模型得到的DIF值在低应变率下相差不大,但在中高应变率(92.03 s-1、166 s-1)下,CSC模型得到的DIF值明显小于实测值,这是由于中高应变率下,CSC模型的盖帽面膨胀和收缩不足,难以准确描述UHPC试件的塑性变形,导致试件部分单元在达到动态抗压强度时提前出现失效,从而降低了模拟效果。

3.3 动态破坏进程对比

为进一步探讨不同损伤模型下UHPC试件在冲击荷载下的动态破坏进程,图6给出了文献[14-16]中UHPC试件在三种损伤模型下的动态破坏进程。图中试件上端为靠近入射杆端,下端为靠近透射杆端。单元失效准则(*MAT_ADD_EROSION)通过定义最大失效主应变εmax来控制,即在冲击过程中自动删除UHPC试件塑性应变超过最大失效主应变εmax的单元。

图6 不同损伤模型下UHPC试件的动态破坏进程Fig.6 Dynamic damage processes of UHPC specimens under different damage models

从图6可以看出,三种材料损伤模型得到的UHPC试件动态破坏进程具有以下共同点:①在冲击加载初期,试件破坏首先发生在边缘单元,试件的核心单元基本上未发生失效破坏,这是由于在冲击作用下,试件轴向受到冲击压缩作用而使径向受到环向拉伸作用,从而导致试件发生轴向压缩变形和边缘单元发生径向拉伸破坏。②随着冲击荷载的增大,UHPC试件内部薄弱层逐渐发展出微裂缝,而且这些微裂缝逐渐聚集,最后贯通成一条或几条宏观裂缝,导致试件最终破坏。③UHPC试件破碎程度随应变率的增加而增大,在低应变率时(60 s-1),试件呈裂而不碎,但随着应变率提高,裂缝开始贯穿整个试件,当应变率为166 s-1时,试件的破坏形态呈明显的块状。

与此同时,三种材料损伤模型得到的UHPC试件的动态破坏进程也具备以下不同点:①对于KCC模型,不同冲击应变率下单元失效由边缘单元逐渐发展到核心单元,试件整体出现压缩变形,表现出明显的整体塌陷现象。②HJC模型模拟的试件破坏进程与KCC模型类似,单元失效均逐渐向内发展,但HJC模型的边缘单元比KCC模型破坏程度更小,并且核心单元出现向外迸裂,即表现出明显的边缘塌陷现象。③对于CSC模型,单元失效由边缘单元发展到中部单元,但没有进入核心区域,由中部单元沿着核心单元形成一个环状破坏区域,核心单元在中部单元的约束作用下失效破坏较少,表现出明显的核心存留现象。