基于UKF的毫米波雷达手势识别算法研究

蒋留兵，朱柏青，车 俐

（1.桂林电子科技大学信息与通信学院，广西桂林 541004；2.桂林电子科技大学计算机与信息安全学院，广西桂林 541004;3.广西无线宽带通信与信号处理重点实验室，广西桂林 541004）

0 引 言

在高度信息化时代，人机交互技术（Human-Computer Interaction, HCI）［1］已成为了各国大力发展的对象。手势识别作为人机交互技术之一，是国内外研究者所关注的热点。目前主要有两种不同类别手势识别：与触摸屏交互的手势识别与无需触摸屏的手势识别。无需触摸屏手势识别市场主流是基于光学传感器、可穿戴设备［2-3］和雷达传感器［4］，其中雷达的手势识别相较于前两者具有不受光照条件影响、不受佩戴设备带来的不适感、成本较低和不侵犯用户隐私数据等优势。

而在雷达传感器中毫米波雷达又以质量轻、体积小、探测性能稳定、穿透烟雾和灰尘的能力强且多普勒频移较大，距离和速度的测量精度与分辨率较高受到研究者们的青睐。在目前的毫米波雷达手势研究中，研究者基本采用将距离-多普勒谱图（Range-Doppler Map, RDM）放入神经网络［5］中提取手势的运动特征实现手势识别。在文献［6］中作者将RDM 和RAM（Range-Angle Map,RAM）相融合，相比仅使用RDM 具有更好的性能。而在现实手势识别场景下，还包含着较多静态干扰和类目标干扰。文献［7］研究了多人场景下使用FMCW 雷达进行手势识别，通过辨别感兴趣距离对潜在干扰进行消除。而在文献［8］中研究并提出了一种重用的LSTM（RLSTM）网络来提取手势距离和多普勒特征，并用领域阈值检测方法来过滤干扰信号。在文献［9］中为了识别两只手所做手势，提出了一种基于小波变换、CFAR和FDM算法应用于RDM的干扰抑制。文献［10］中作者设计了一套完整的目标干扰抑制方法，提出了SIS和DIS算法，并利用膨胀三维网络（TS-I3D）进行手势特征提取和分类。在实际应用中，面对类目标干扰，绝大多数选用目标跟踪算法实现干扰抑制。常用的跟踪算法为卡尔曼滤波（Kalman Filter，KF）［11］。而手势动作多数属于非线性动作，所以扩展卡尔曼滤波（Extended Kalman Filter,EKF）［12］和无迹卡尔曼滤波（Unscented Kalman Filter,UKF）［12-13］比KF 更适合处理非线性系统。在文献［14］中，作者提出对于雷达跟踪中的非线性数据滤波问题，EKF 数据图像精度对于雷达跟踪数据滤波并不理想，而UKF 能够得到更准确的结果，可以达到更好的性能。因为非线性函数的均值和协方差矩阵可以通过无迹变换更准确地估计出来,并且通过避免计算雅可比矩阵，显著降低了计算复杂度。

在本文中，将不同手势对应不同的运动模型，并针对实际情况，对部分运动模型进行改进。将设计好的手势运动模型利用无迹卡尔曼滤波算法进行轨迹预测，得到与雷达原始数据帧数相同个数的轨迹信息（距离和多普勒信息）。将预测好的信息放入K最临近分类器（K-Nearest Neighbor,KNN）中，与原始数据中包含的所有信息进行分类，与预测信息分为一类的属于手势原始数据中目标手势类，其余为类目标干扰类，并将类目标干扰权重置为零，以达到类目标干扰抑制的效果。最后将干扰抑制后特征谱图放入CNN［15］进行特征提取实现识别。

1 FMCW雷达信号模型、特征提取及数据预处理

在本论文中，采用调频连续波（Frequency Modulated Continuous Wave, FMCW）雷达对目标手势和类目标物体进行采集。1.1 节中对FMCW 雷达信号模型进行简要描述，在1.2 节中对由中频信号估计距离和多普勒信息过程进行简要描述，并在1.3 节中介绍了针对RD 图中背景噪声太大导致目标难以检测的情况进行原始数据预处理的过程。

1.1 FMCW 雷达信号模型

FMCW 雷达发射出线性调频信号，而线性调频信号又称Chirp 信号。发射Chirp 信号过程中，在实验场景中遇到目标会产生反射信号被雷达接收天线接收，在雷达内部与发射信号混频得到中频信号。在本文中采用的是锯齿波，如图1所示。

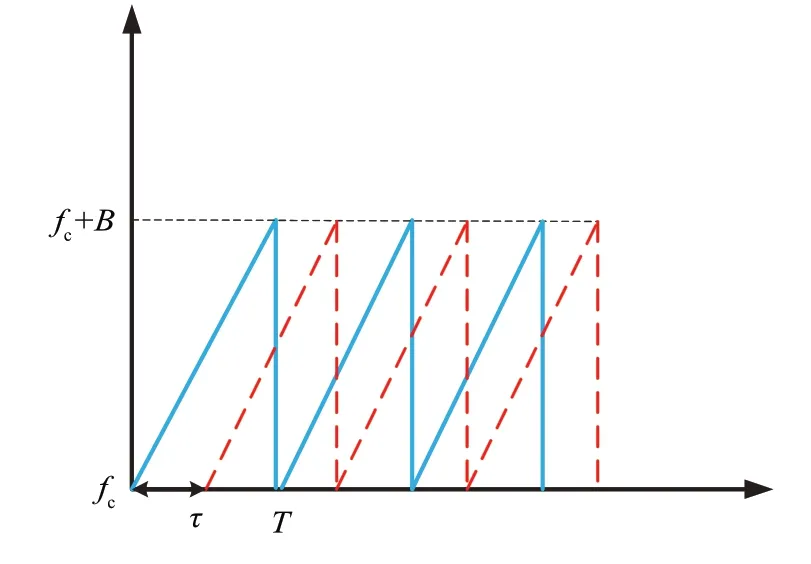
图1 FMCW雷达波形图

在FMCW 雷达中，单个Chirp 发射信号表达式为

式中，AT为发射天线的增益，fc为载波中心频率，K=B/T，代表调频斜率，其中B表示信号带宽，T表示Chirp的持续时间。于是信号瞬时频率为

目标反射的回波信号表达式为

式中，AR为接收信号振幅，τ为回波信号时延，fd为多普勒频移。

在得到回波信号后，我们将发射信号与其混合后传递到低通滤波器，获得中频信号，中频信号表达式为

式中φ(θ)表示相位，AIF表示中频信号功率。

1.2 距离和多普勒（速度）信息估计

目标距离信息可以根据回波时延τ和信号速度c由公式（5）得到：

但在实际中回波时延τ非常小导致难以估计，所以经常采用中频信号频率fIF来估计τ，距离信息可以用公式（6）表达：

面对运动目标，FMCW 雷达的发射信号与接收信号之间存在着一定的频率差Δf而这个频率差就称为多普勒频率fd，所以多普勒信息可由公式（7）得到：

式中λ为雷达信号的波长。

在本文中，我们用128帧雷达数据完整描述手势动作，每帧包含128 个Chirp，而每个Chirp 中采样128 个点，所以一个数据会形成一个128×128 的二维矩阵，如图2 所示。然后分别在快时间维度（距离维度）和慢时间维度（多普勒维度）作快速傅里叶变换（FFT），提取出目标距离和多普勒单元，最后根据相位差得到RDM。

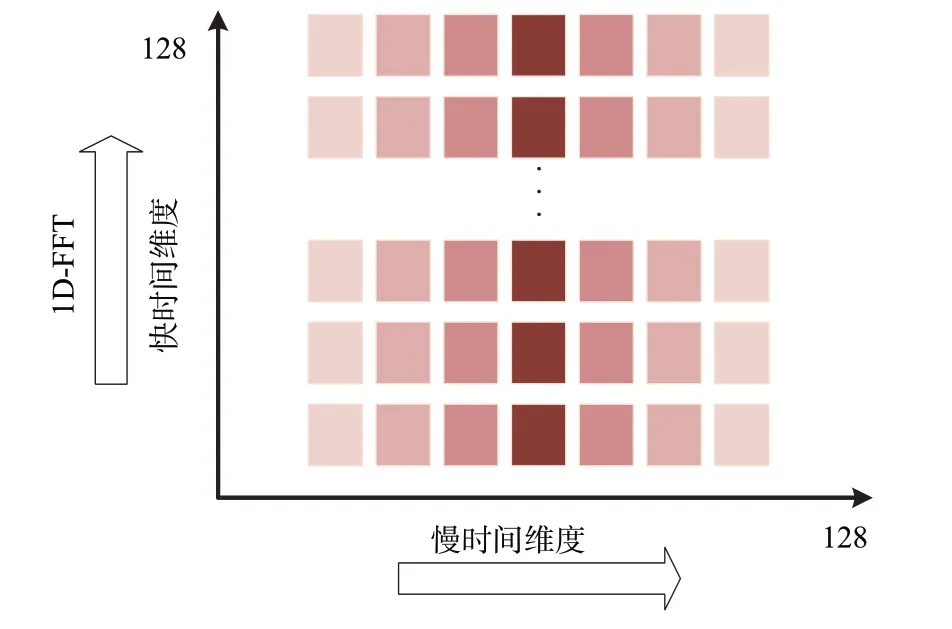
图2 距离-多普勒特征提取原理图

1.3 原始雷达数据预处理

在得到RDM 后，我们发现RDM 上目标周围存在大量背景噪声，同时能够检测到多个目标，这将使得后续识别部分难度提升。本文利用单元平均恒虚警率算法（Cell-Averaging Constant False Alarm Rate,CA-CFAR，如图3 所示）进行背景噪声滤除和目标检测。

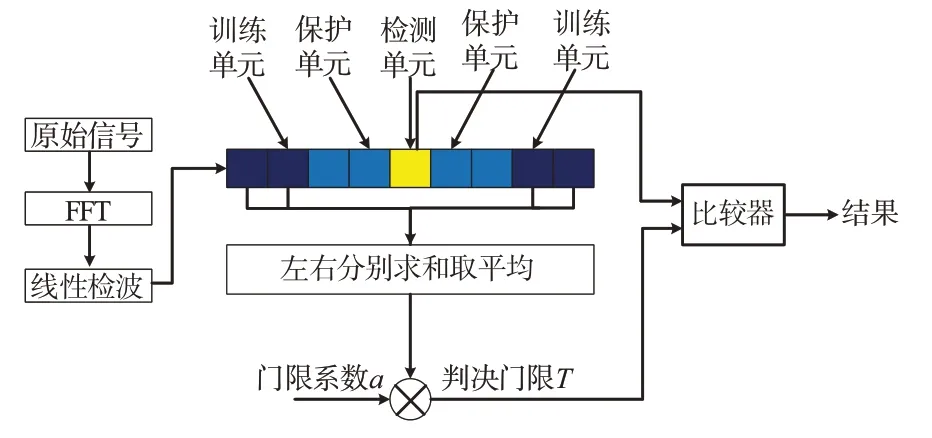
图3 CA-CFAR检测器原理图

脉冲回波包括检测单元、保护单元和训练单元。本文采用的CA-CFAR核心思想就是通过对参考窗内采样数据取平均来估计杂波功率，当信号振幅大于杂波功率时，确定有目标。当振幅小于杂波功率时，将其视为噪声。

2 类目标干扰抑制算法设计流程

在原始数据进行预处理之后，原始RDM 中背景噪声分量已经得到了基本抑制与消除，但预处理之后的RDM 中能够检测到手势目标、静态类目标和动态类目标，严重影响手势目标特征提取。为此本文提出一种U-IS 算法（Unscented Kalman Filter-Interference Suppression)，算法主要由UKF 与KNN 组成。U-IS算法具体流程如图4所示。在2.1节中介绍了针对不同手势设计的不同运动模型。在2.2 节中介绍了跟踪和估计手势运动轨迹的基本算法（UKF）。

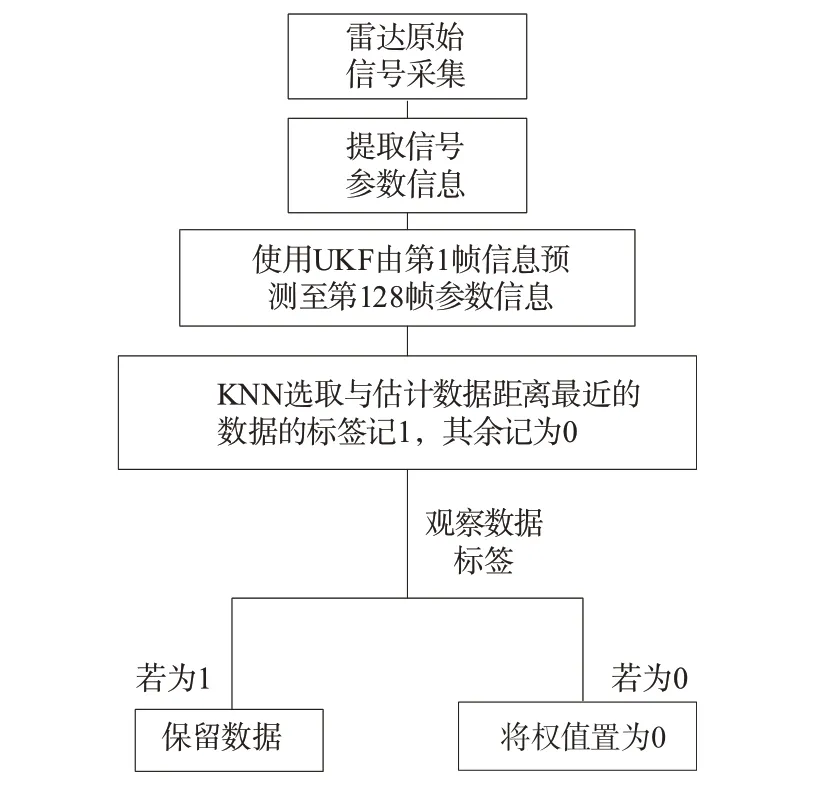
图4 U-IS算法流程图

2.1 手势运动模型设计

在本文中分别以前推、后拉、左移、右移、顺时针旋转和逆时针旋转6 种手势进行识别。按照运动特性和轨迹来分类，前推和后拉、左移和右移、顺时针旋转和逆时针旋转两两使用同一种运动模型。

2.1.1 前推、后拉手势模型

因运动方式简单，我们将前推和后拉手势设定为一个等速模型（Constant Velocity, CV）。以雷达为原点建立二维坐标系，目标手势在y轴上作匀速直线运动，如图5所示。

图5 前推和后拉手势运动模型效果图

手势模型的状态空间可以由公式（8）表示：

其中Px和vx为零。而转移函数如公式（9）所示：

2.1.2 左移、右移手势模型

对于左移和右移，同样选取CV 等速模型，跟CV1模型建立同类坐标系，目标手势面对雷达作左右匀速直线运动，如图6所示。但模型的状态空间与前推和后拉的手势模型状态空间有所不同，如公式（10）所示。

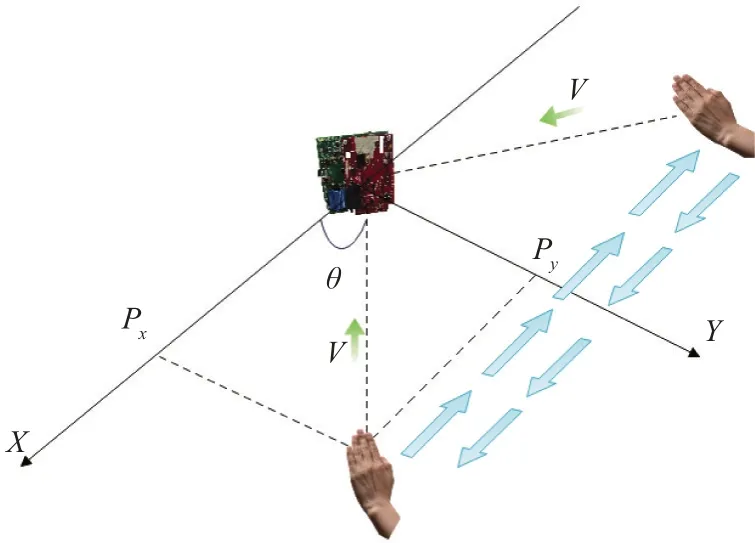
图6 左移和右移手势运动模型效果图

4 个状态变量依次为手势对应坐标系中的横坐标、纵坐标、与x轴夹角（逆时针为正）、速度。状态转移方程如公式（11）所示：

2.1.3 顺时针和逆时针旋转手势模型

对于时针手势，运动模型设计复杂，涉及状态变量较多，为解决传统二维恒定转率和速度模型（Constant Turn Rate and Velocity, CTRV）难以描述运动手势问题，本文基于CTRV 模型提出了三维恒定转率和速度模型（Three Dimensional CTRV, 3DCTRV）如图7 所示。此运动模型更加适合时针运动手势。

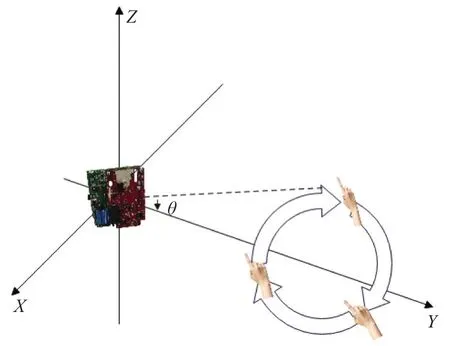
图7 顺时针旋转和逆时针旋转运动模型效果图

设此组手势动作状态空间变量为

7个状态变量依次为手势对应坐标系中的x轴坐标、y轴坐标、z轴坐标、圆周云顶半径、线速度、转速、角速度。其中匀速圆周运动线速度的大小等于质点通过的弧长s与时间t的比值。弧长公式为

所以弧长对应的弦长公式为

由此可知CTRV模型的状态转移方程为

2.2 无迹卡尔曼滤波算法

在本文中，毫米波原始数据预处理后采用UKF 对目标手势动作轨迹信息进行预测和估计，相较传统KF 算法，UKF 能够更好地解决现实场景中非线性问题。而相比同样适用于解决非线性问题的拓展卡尔曼滤波，UKF 与其思想基本相同，但Sigma 点近似非线性转换的效果比线性化更好，也避免了雅可比矩阵的计算，降低了计算的复杂度。图8 展示了EKF 与UKF 的区别和UKF 使用Sigma点近似非线性分布的基本原理。

图8 EKF与UKF区别、UKF利用Sigma点近似分布

UKF 分为预测阶段和测量阶段。预测阶段操作为无迹变换过程。本文将分别在2.2.1节和2.2.2节中详细介绍预测阶段和测量阶段。

2.2.1 UKF预测阶段

1）计算Sigma 点集：首先对Sigma 点数量n的选择取决于实际手势系统的状态维度N。例如左划手势包含4种状态维度，所以对左划手势进行无迹变换需要9个Sigma点。

每个Sigma点的计算公式为

本文根据公式（17）计算Sigma 点矩阵，其中公式（17）中第一个公式代表的是均值点，本文对于初始均值点选用的是雷达手势数据第一帧包含的维度信息。其余点都是围绕均值的Sigma 点。λ为比例因子，λ大小代表应该选择距离均值多远的Sigma点，Σ代表初始协方差矩阵。

2）计算Sigma点权重：在选择出来我们需要的Sigma 点，应该为每个Sigma 点赋上合适的权重。权重的计算公式为

式中k和α影响着Sigma点与均值点距离，λ为扩散函数，β取值为2 是高斯分布的最佳选择。本文将k设为1，α设为0.75。

3）计算近似高斯分布均值和协方差：我们得到了带有权重和非线性等式转换的Sigma 点，然后可以通过Sigma 点近似新的高斯分布，并计算其均值和协方差。计算公式如下：

式中μ′表示预测均值，Σ′表示预测协方差，g表示预测方程即手势运动模型。实际场景中，包含着许多不确定性，所以Rt代表着过程噪声。至此，UKF的预测阶段介绍完毕。

2.2.2 UKF测量阶段

经过预测阶段，我们得到了预测值均值和协方差矩阵。当我们得到来自雷达的测量值后（本文选用雷达第二帧包含的维度信息），需要计算出预测值和测量值之间的差值，我们得从预测的状态空间转换到测量状态空间，依赖公式（22）中h(x)。

式中，Z代表测量空间中Sigma 点集，x则为预测阶段得到的Sigma 点矩阵，ẑ是测量空间均值，S和Q分别代表测量空间协方差矩阵和噪声。在FMCW雷达中，h(x)表达如公式（25）所示：

式中，ρ、φ和̇分别代表测量目标手势在手势坐标系下与雷达距离、目标手势与x轴夹角以及目标手势与雷达相对距离变化率。

之后我们需要计算卡尔曼增益K，想要得到卡尔曼增益需要计算预测空间中Sigma 点与测量空间中的Sigma点之间的交叉关联矩阵T。公式（26）和（27）给出了T和K的表示式：

最后利用卡尔曼增益得到我们想要的手势目标下一帧状态信息预测：

3 实验过程及结果

本文实验中采用德州仪器公司（Texas Instruments, TI）生产设计的AWR1843 雷达和DCA1000数据采集卡（如图9 所示）采集手势目标和类目标。设定雷达有1 根发射天线和4 根接收天线，频率设置77～81 GHz。选择6 种手势：前推、后拉、左移、右移、顺时针旋转和逆时针旋转。对雷达参数配置如表1 所示，针对表1 帧数选择，主要考虑本文选取的6 种手势动作一次运动时间，雷达采集一次数据时间取决于采样周期、采样点数、Chirp 数与帧数。其中前三项参数分别与速度和速度分辨率有关，所以我们通过调整采集帧数来控制采集时间。若缩小帧数，会导致雷达无法采集完整手势动作，而增大参数会导致手势数据中部分没有手势动作，生成的RD 图不利于识别，降低识别性能。

图9 AWR1843雷达传感器和DCA1000数据采集卡

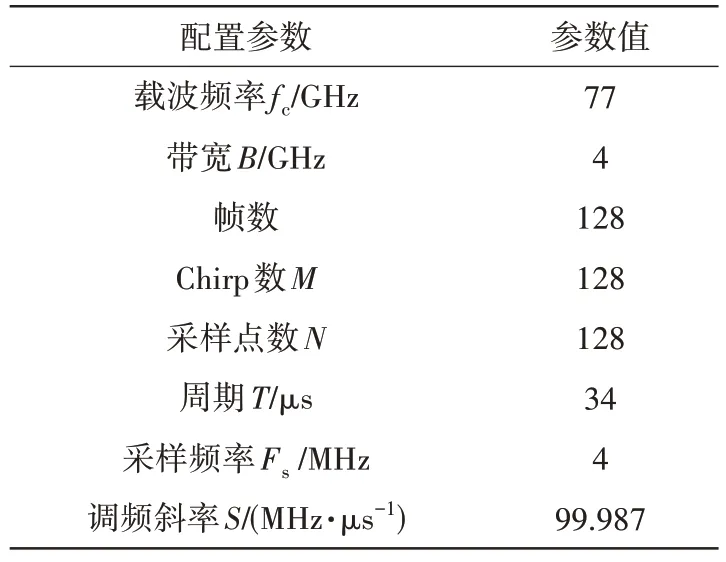
表1 雷达参数配置表

设定目标手势位置距离雷达0.5 m 左右，在距离雷达1.6 m 左右设置一个来回运动的人作为类目标干扰，实验场景如图10 所示。在雷达的检测范围内，主要可检测到的目标有目标手势、采集者的静止躯干、随着手势运动的躯干目标、固定位置的铁板和在采集者身后运动的目标。

图10 手势采集场景

3.1 原始数据预处理

本文采用CA-CFAR算法对雷达原始回波数据进行预处理，可以有效地去除背景噪声。

我们以顺时针手势RD 图为例，预处理的效果如图11所示。

图11 原始数据预处理前后RDM比较

图11（a）是原始数据经过1D-FFT与2D-FFT之后得到的RDM，图11（b）是在图10（a）基础上进行了背景噪声干扰消除后的RDM。从这两幅图比较可以看出，原始RD 图在检测到目标周围散布着大量噪声，严重影响后续识别操作，经过预处理之后的RDM 明显地消除了背景噪声，使得RDM 更加直观。

3.2 U-IS算法抑制类目标干扰

在原始数据进行预处理之后，采用U-IS 算法对类目标干扰进行消除。首先利用UKF 算法对128 帧雷达数据包含的主要维度信息（距离和速度）逐帧预测。预测结果如图12所示。

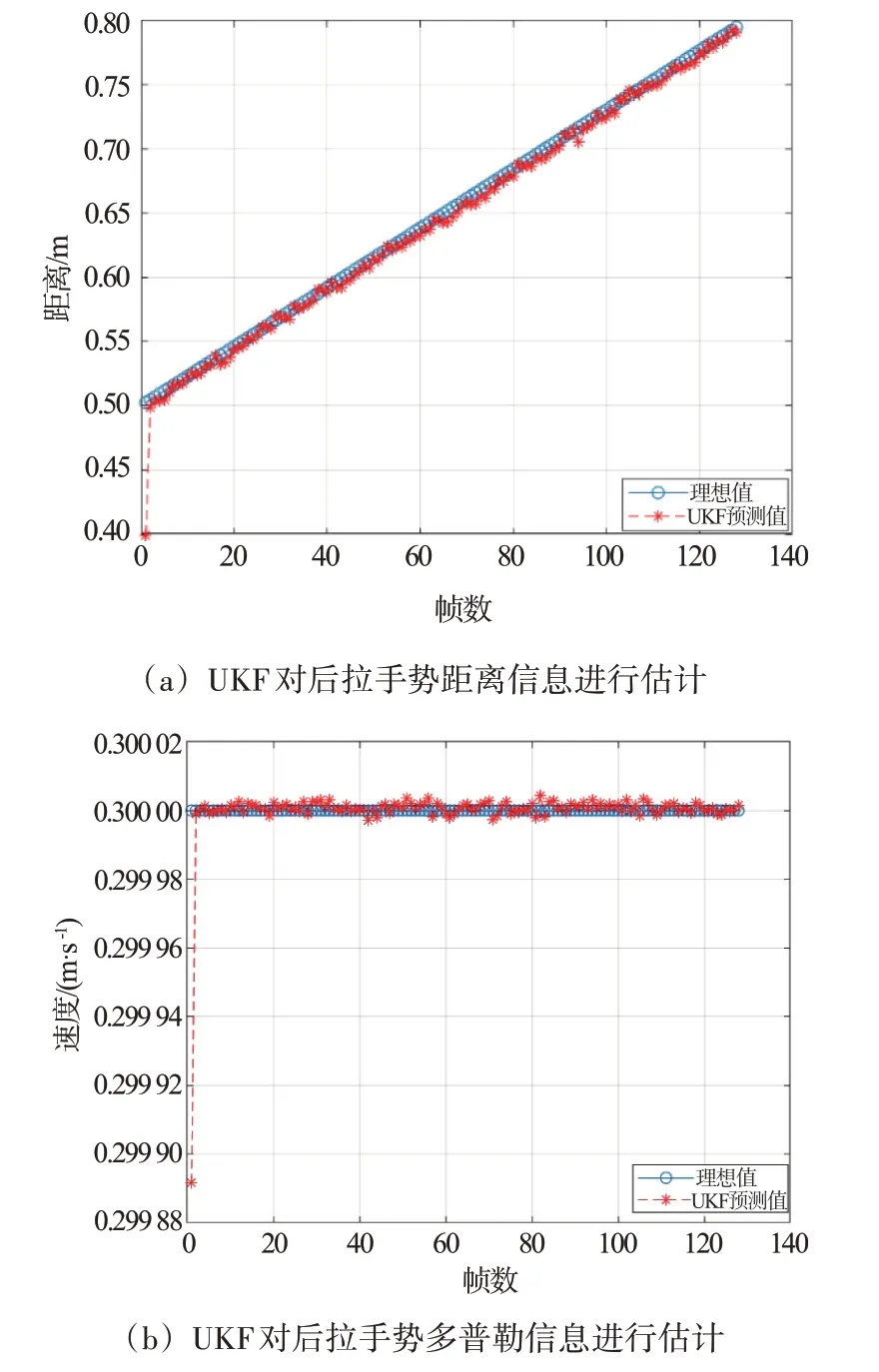
图12 UKF对后拉手势各参数信息进行估计

图12（a）是UKF 对后拉手势距离信息从第1帧到第128 帧的估计数据，图12（b）是UKF 对后拉手势速度信息从第1 帧到第128 帧的估计数据。从图12 可以看出，UKF 可以对雷达每一帧数据进行预测和估计。我们得到经过UKF 的预测值并将其与原始数据中包含的参数值放入KNN 中进行比较，将UKF 预测值的标签设定为手势目标，将在原始数据中与UKF 预测值距离最近的128 个点归为目标手势一类，其余数据点则为类目标干扰，并将类目标干扰在RDM 中的权重设置为0，效果如图13所示。

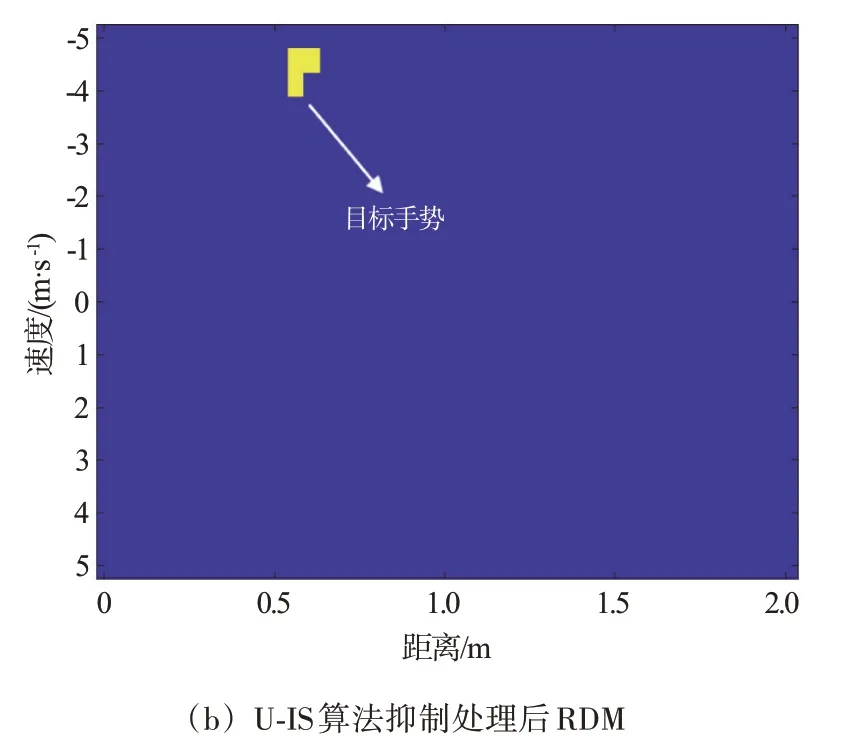
图13 U-IS算法使用前后RDM比较

图13（a）是在进行U-IS 干扰抑制算法之前的RDM，图13（b）是U-IS 干扰抑制算法处理后的RDM，比较两幅图可以看出U-IS 算法可以很好抑制RDM中类目标干扰。

3.3 手势识别性能分析

将本文设计的6 种手势每种采集150 个数据。6 种手势总样本数为900。我们以8∶2 的比例划分训练集和测试集进行识别实验。

为了达到比较手势识别效果的目的，本文建立了两个数据集，一个是干扰抑制前RDM 数据集，另一个是经U-IS 抑制算法进行干扰抑制后的RDM 数据集。本文采用CNN 网络，设置学习率为0.000 1，迭代步数设为250 次。经过250 次迭代后，干扰抑制前后的识别准确率和损失值曲线如图14 所示。

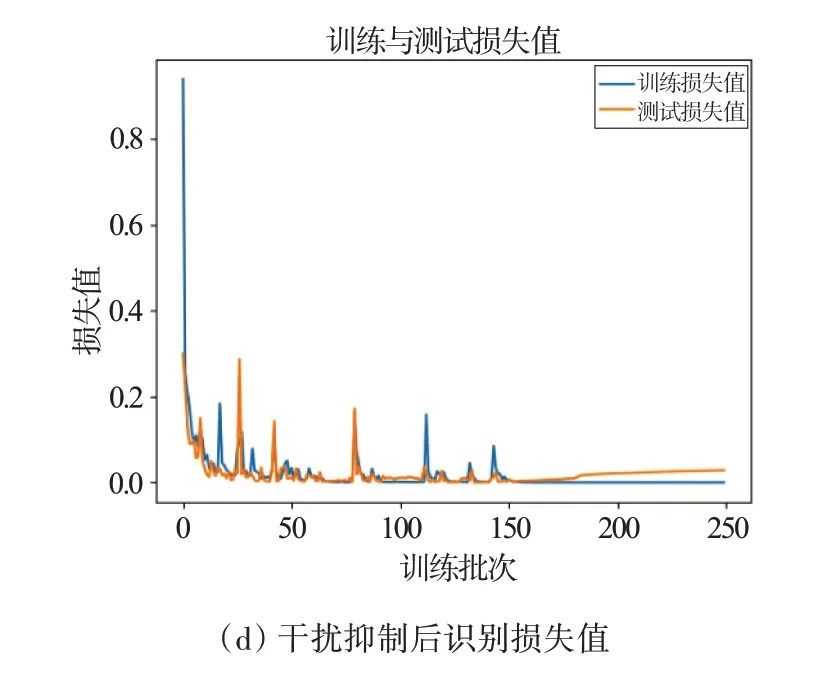
图14 干扰抑制前后手势识别准确率与损失值对比

由图14（a）与（c）的对比可以看出，干扰抑制前的准确率低于干扰抑制后的准确率，且训练过程中准确率很不稳定，波动较大。由图14（b）与（d）的对比可以看出，干扰抑制后数据集的损失值较低且稳定。在识别过程中若出现获取的手势样本数量不能够完全覆盖各种手势情况的问题时，可以对RDM样本进行数据增广，具体方法有平移、旋转、反转、错切和组合变换等。通过这些方法将数据集扩充到足以覆盖观测范围内各种手势情况，以提高识别性能。

表2 显示了在相同网络和不同数据集下6 种手势识别的准确性。由表中可以看出，经过U-IS算法处理之后的数据集比干扰抑制前数据集具有更高识别准确率。干扰抑制后的平均识别准确率达到了98.74%，相较于干扰抑制前的平均识别准确率91.45%有着较大提升。

表2 手势识别准确率对比

3.4 干扰抑制方法对比分析

通过将本文提出的U-IS 方法与其他论文所提出方法进行比较，进一步验证所提方法的有效性。所选对比方法为文献［8］和文献［9］中所提出，简要描述如下：

1）小波变换-CFAR-FDM：该方法选择sym4 母小波作为基函数，并对RDM 进行了三级多尺度小波分解实现动态类目标的干扰抑制，再通过CFAR算法与FDM（Frequency-Division Multiplexing）算法的组合对静态类目标干扰进行消除。

2）SIS-DIS：作者分别提出了SIS（Static Interference Suppressions）和DIS（Dynamic Interference Suppressions）算法。对于SIS 算法，是对于所有多普勒参数为零目标在范围向量进行排序，若前一时刻目标数量不相等则删除重复目标以达到静态干扰的消除。DIS 算法则是将所有目标按照范围排列，如果距离最小则记录多普勒，如果多普勒中正数大于负数则记录成类目标，否则记录成手势目标。

将原始数据分别按照上述两种方法进行类目标干扰抑制后，得到的RDM 数据集分别放入与本文选择的同一种网络CNN 中进行训练与测试，其结果对比如表3所示。

表3 不同干扰抑制方法最终识别精度对比

通过表3中数据对比分析可知，经过使用本文所提出的干扰抑制方法抑制后的数据集相较于WT-CFAR-FDM 方法在各个手势动作的识别准确率上都有一个较大的提升，而相较于SIS-DIS 方法，在前4 种动作上的识别精度相差甚少，而在时针运动轨迹手势上，由于本文方法为此类易混淆手势设计了运动模型，所以在顺时针与逆时针旋转手势识别精度上有着显著提升。

4 结束语

本文提出了一种基于UKF 的毫米波雷达手势识别方法。首先通过预处理消除了手势信号中的背景噪声与干扰，再通过UKF 对手势参数信息进行预测和估计，将预测估计得到的参数信息与原始参数信息放入KNN 中进行分类，消除了实验环境中的静态干扰和动态干扰。然后利用CNN 网络提取手势特征，结果表明，本论文实验采用的U-IS干扰抑制算法较无干扰抑制准确率提高7.29%，手势识别的平均准确率为98.74%。