基于物理模型的级联生成对抗网络加速定量多参数磁共振成像

刘羽轩，楚智钦，张煜

南方医科大学生物医学工程学院//广东省医学图像处理重点实验室，广东 广州510515

多回波多参数定量磁共振成像（qMRI）是一种定量MRI［1］的成像技术，它利用多回波图像获得多对比度图像来量化组织性质。与广泛使用的定性MRI有很大不同的是，定量MRI通过获得多对比度图像来重建参数图，如定量质子密度加权（PDW）、T1弛豫时间等组织参数映射、定量T2*Map［2,3］映射等。这种多参数图可以提供关于医学图像解剖结构特征的互补的定量信息，为特定的组织组成和微观结构提供更多的见解。然而，多参数MRI需要对解剖结构进行多次成像，通过多个翻转角（FA）、回声时间（TE）和重复时间（TR）产生不同的对比进行参数量化。对所有组织类型的时间信号演化的要求可能导致过长的扫描时间，这将增加个体的不适感和在采集过程中产生运动伪影。因此，在保持良好图像质量的同时，开发一种加速多参数MRI成像的重建技术至关重要。

从欠采样的k空间重建高质量图像是加速多对比度磁共振成像的主要策略，但这是一个没有解析解的逆问题。对于定量MRI，传统的定性MRI重建方法如并行成像［4-6］（PI）和压缩感知［7-9］（CS）可以获得多对比度图像，然后采用物理模型进行参数图估计。然而，当加速速率较高时，这些传统的方法会出现残留的伪影混叠现象。基于深度学习的MRI 重建方法已被提出［10］，包括独立的去噪网络和解卷级联网络［11,12］。基于卷积神经网络［13-23］（CNNs）的方法被提出来去进一步增加加速因子和提高重建质量。遗憾的是，这些研究没有充分利用输入数据，特别是在处理小数据集的时候。例如，在一些研究中［11,14-20,23］，输入数据只在图像域进行处理，而在频域和图像域同时进行处理可以获得更好的图像重建效果［13,21,22］。此外，生成对抗网络（GANs）也被用于MRI重建工作［24-26］，这些方法通过引入GAN来让输出的重建图像学习全采样图像的数据分布，但它们无法与同时涉及多域联合训练的方法相比。并且，使用相同的U-Net网络，特别是简单的池化和上采样层应用于频域和图像域信息，对频域恢复和图像重建并不是最合适的［27］。另一方面，单一地使用像素差值类型的损失函数并不能充分约束重建损失以提高重建图像的质量，重建的质量并不只受到像素之间差值的影响，也与图像的对比度、亮度和相似性有关［28］。

除了网络结构设计问题外，数据的预处理和使用显得更为重要。例如，数据的不正确处理又会导致很多算法都只能止步于实验阶段，缺乏实时性也无法真正落地即实验与真实场景使用数据形式不一致。其次，医学图像数据的收集困难，通常只能从少量的样本中提取信息，但是，要想进行有效的深度学习训练，就必须收集大量的训练数据。通过结合物理驱动的深度学习重建方法，可以有效地解决k空间到图像域或者图像域之间的映射问题，从而提高模型的泛化能力，减少训练数据量，并且可以更好地学习和预测模型的最优参数。然而，在许多加速定量磁共振成像研究中［29-32］，采样数据的选择和网络结构的设计仍然没有摆脱单线圈数据的使用和基于数据驱动处理的模式弊端。而我们都知道，实际使用大多都是多线圈数据，将传统重建方法中的物理原理和深度学习结合起来，能实现比基于数据驱动方式更好的结果。

1 方法

1.1 总体结构

本研究所提出的框架由两个部分组成（图1）。第一部分是利用深度学习网络对多回波图像进行重建。然后利用重建后的多回波图像进行基于物理模型的最小二乘拟合以获得多对比度多参数图像。给定欠采样的多回波梯度回波序列 k 空间数据Y={Y1,Y2,…,YT}∈CT×C×N，其中N=Nx×Ny，并且Yi∈CC×N，其中i=1,2,…,T是第i个多线圈复值欠采样回波k空间数据，N表征每个线圈数据的像素数量以及C为总的线圈数，T是总的回波数。由于二维多回波多线圈数据的巨大内存消耗，本研究在读出方向（RO）中执行二维图像重建，在RO方向全采样而相位编码（PE）和空间相位编码（SPE）其他两个方向则处于欠采样的条件约束。Nz表示读出方向上的总层数，其中（s=1,2,…,Nz）。为了更好的描述多回波磁共振成像系统，本研究定义:

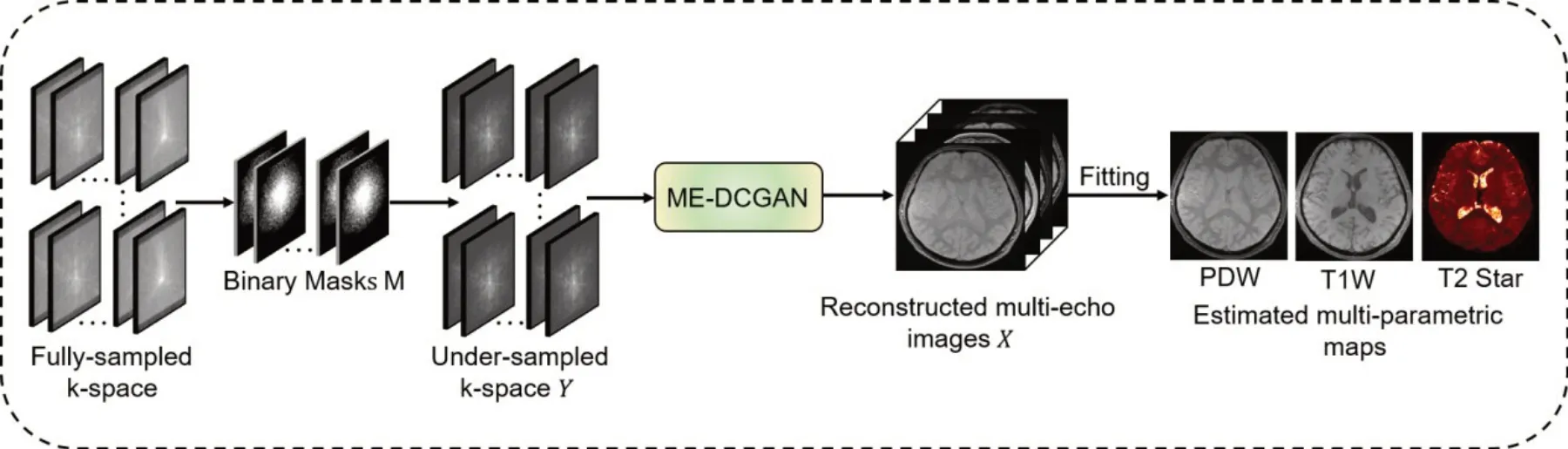
图1 网络框架Fig. 1 Overall architecture of the proposed method.

其中X∈CT×N表示重建的多回波图像，并且b∈CT×C×N表示高斯噪声，这有利于异常点的重建。操作算子A作用于系统矩阵并且通常可以被定义为:

其中M={M1,M2,…,MT}表示多回波采样矩阵，每个矩阵Mi∈{0，1}N×N，F表示二维离散傅里叶变换，S∈CC×N×N表示线圈敏感度图。

由于加速MRI重建是一个没有解析解的逆问题，需要对输出图像X进行正则化来限制解空间。通常，优化问题可以表述为:

以λ∈R作为平衡数据保真度项和正则化项R(X)的权重。为了同时有效地处理实部和虚部数据，本研究将Y分为实部和虚部两个通道送入到本研究的重建网络中。本研究的网络包含生成器和判别器，它们迭代数为p(p=1,2,…,K)次，K为总的迭代次数，每次迭代后网络的性能都会得到提升。图2A展示了所提出的网络架构，我么可以将重建的回波图像进行后处理以得到多参数多对比度的图像例如PDW、T1W以及T2*Map。合成的方法如下所示:

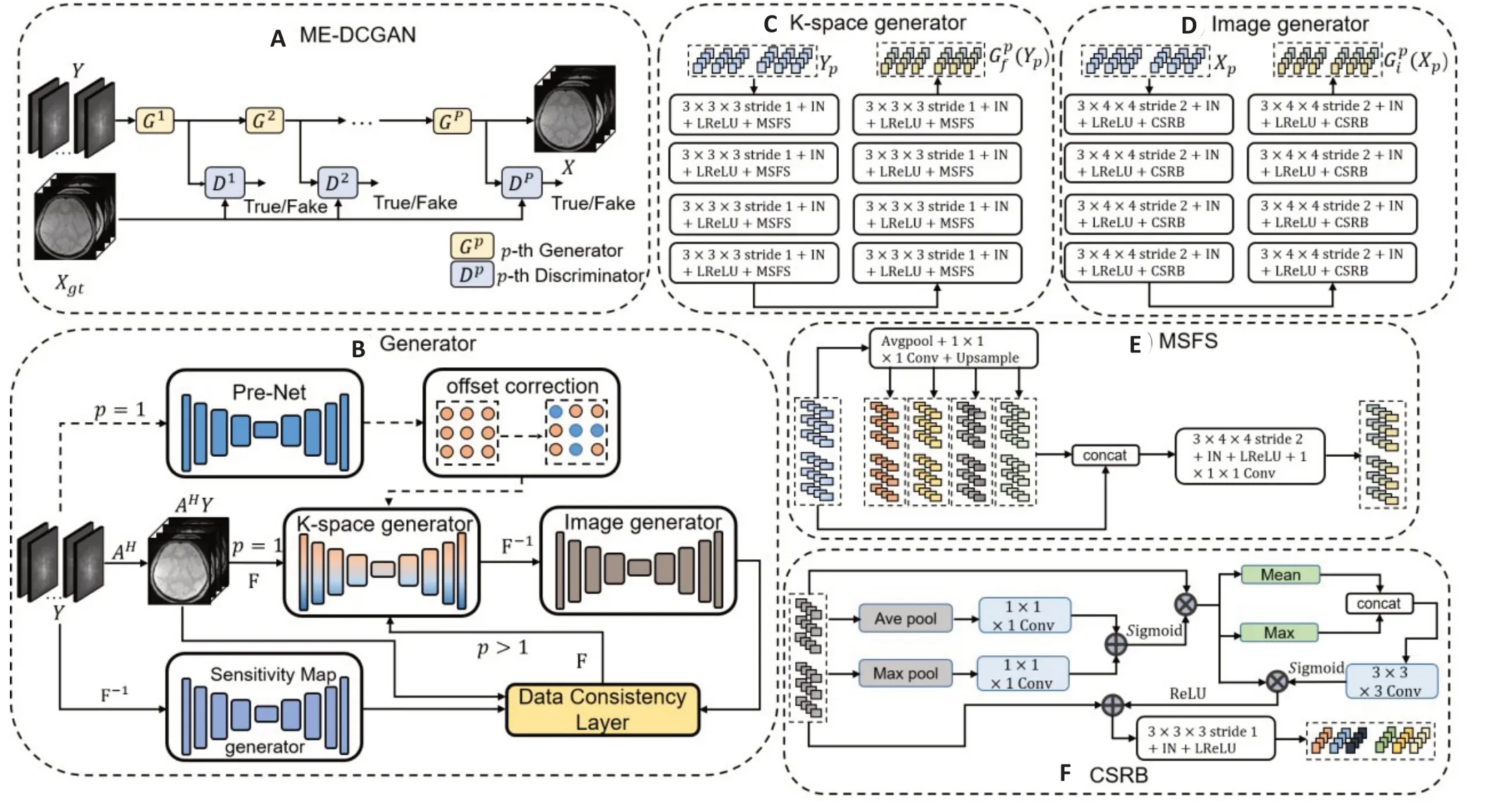
图2 基于物理模型的级联的生成对抗网络的多回波磁共振重建框架图Fig. 2 The physical model-based framework for accelerating multi-echo MRI reconstruction with cascaded generative adversarial networks.Where A-D represent the overall network framework,the complete generator structure,the K-space and image generator and E,F denote the MSFS and CSRB module separately

Xi∈CN表示重建的单个回波图像，T2*Map映射计算采用MDI方法［3］。

1.2 生成器

生成器（G）由k空间生成器Gf、图像生成器Gi、线圈敏感度图生成器Gs和数据一致性层［12］（DC）组成。一次迭代后，图像生成器的输出将被输送到上一个的k空间生成器中以提供额外的监督信息。k空间生成器、图像生成器和数据一致性层的每次迭代都共享相同的参数。生成器的优化过程如下所示:

生成器的结构如图2B所示。

1.2.1k空间生成器 在k空间生成器中，卷积层由3×3×3 卷积核、实例归一化（IN）层和校正线性操作单元（LReLU）组成。具体来说，最后一层只有1×1×1的卷积运算。由于输入的不是真正意义上的三维数据，而是多回波二维数据，因此仅在二维空间减少特征图像分辨率大小，而卷积操作仍然在三维空间中进行。k空间信号具有全局信息。为了避免特征空间中频域信息的丢失，本研究提出采用多尺度特征融合采样层（MSFS）来代替池化层和上采样层。此外，本研究使用预训练网络提供偏移校正的频域信息，以获得接近全采样频域信息的频域特征图。

预训练的网络是U-Net。本研究只在第一次迭代网络中引入预训练网络。MSFS模块的详细结构如图2E 所示。其中，B为批处理大小，E为通道数，T×H×W为三维特征图的维度。本研究定义第p个k空间生成器的输入为Yp，第p个k空间生成器的损失包含均方误差损失，可以表示为:

1.2.2 图像生成器 图像生成器使用与k空间生成器相同的卷积、归一化和激活函数，但将池化层替换为卷积核为3×4×4 步幅为2的卷积。本研究定义第p个图像生成器的输入为Xp，由图像域与频域之间的关系可得到:

其中F-1表示二维离散逆傅里叶变换。由于多回波二维图像丢失了三维空间结构信息，因此利用特征图通道残差块和空间特征表示模块（CSRB）增强特征信息是解决空间结构变化引起的结构信息丢失问题的可行方法。CSRB模块的详细结构如图2F所示。此外，本研究使用了绝对误差损失、均方误差损失、梯度差异损失和结构相似性损失［29］的组合损失函数来保持良好的图像细节。绝对误差损失L1和均方误差损失L2可以表征为像素误差损失。本研究定义第p个图像生成器的像素误差损失为:

实际上，在系统矩阵A中，线圈灵敏度图S也是未知的，需要进行估计。需要注意的是，由同一线圈获得的多回波数据具有相同的灵敏度图S。本研究采用UNet作为线圈敏感度图生成器，其可以表示为：

其中，RSS表示平方求和开根运算符。

1.3 判别器

判别器采用PatchGAN结构［33］。直接端到端映射将影响多回波图像重建质量。因此，结合来自迭代网络的每个损失，可以有效地提取潜在信息，提高模型的表达能力。为了让迭代网络的每个损失更加符合模型的训练过程，本研究基于指数衰减的模型［12,13］的总损失可以表示为:

其中mul表示逐元素相乘算子。

1.4 统计学方法

使用python stats 库中的t检验来计算P值，当P＜0.05时认为差异有统计学意义。

2 结果

2.1 数据集

本研究使用了三维MULTIPLEX（MTP）获得的多回波多线圈内部数据，这是最近提出的一种用于多参数脑映射的新序列［34］。特别的是，MTP是一种具有双重复时间（TR）、双翻转角度（FA）和多回波设计的梯度回波脉冲序列（GRE），以提供不同的对比度。MTP采集在3T扫描仪（890）上采用32通道头线圈，使用以下参数：FA1/FA2=4/16，每个翻转角获取6～8个回波同时回波时间（TE）=3.9～20.8ms，两个TR的值都为34.5ms，矩阵大小为256×256×80，体素大小为1×1×2mm3。本研究可以灵活的设计MTP序列的参数比如TR，TE，FA，层厚以及FOV。数据集包含20名受试者，共计284个回波，每一个全采样受试者的中心40个切片，包含相应的脑组织，16/2/2名受试者（640/80/80）切片作为训练、验证和测试，一个完整的受试者的全采样图像所需时间为14 min。

2.2 实验设置

本研究对比了传统方法ESPIRIT［35］，级联CNN网络（DC-UNet）［18］，生成对抗网络［27］和本研究设计的方法（ME-DCGAN）。所有模型都在PyTorch中训练，使用NVIDIAGeForce RTX 3090显卡和24GB GPU内存，使用Adam优化器，参数β1=0.5 以及β2=0.999，学习率为1e-3，共训练50次，批处理大小为1。所有对比方法均使用它们的默认参数设置重新训练。评价指标包括峰值信噪比（PSNR）、结构相似指数（SSIM）和归一化均方根误差（NRMSE）。本研究应用权重变量[ε，α，β，γ，ω]的权值为[5，1000，1000，0.001，1]，判别器损失函数的权值设为0.1。增加展开级联迭代次数会增加计算成本，初步实验表明，当迭代次数超过3次时，重建效果不明显。因此，本研究使用最大迭代次数p为3来训练所提出的模型。

2.3 实验结果

对所有重建的多回波图像和多对比度图像而言，ME-DCGAN 模型的PSNR 和SSIM 最高，NRMSE 最低，与传统ESPIRIT方法相比，重建指标PSNR、SSIM和NRMSE的提升接近20%，与基于深度学习的对比方法DC-UNet［18］和Shaul［27］相比，其指标也能提升5%左右（表1）。本文中所有的方法均使用python stats库中的t检验来计算P值，计算结果表明重建的多回波图像和拟合的多参数图像与全采样的图像相比均具有统计学意义（P＜0.05）。对于重建后的多回波图像，对比方法在拟合过程中均使用相同的物理模型获取多对比度多参数图像。因此，对于多对比度多参数图像，本研究的方法在PDW和T1W具有最高的PSNR。尽管T2*Map的PSNR较低，但本研究的方法仍然在定量上优于其它的对比方法，并且本研究的方法也重建出更为清晰的大脑灰质、白质和脑脊液特征。虽然DC-UNet通过级联多个图像域U-Net去噪网络恢复了较为精确的图像细节，但是只需级联一次的ME-DCGAN网络比级联三次的DC-UNet具有更好的图像细节和特征恢复性能，更高的重建指标以及更鲁棒的实验过程与结果分析。这表明了在模型参数量大致相等的情况下混合域学习具有比单域学习更大的优越性以及对图像细节的敏感性。本研究方法的重建指标对比Shaul等［27］的工作表明使用相同的网络结构在频域恢复和图像重建中并不是最合适的。由于频域与图像域的差异，我们需要设计不同的网络结构来特具化地恢复频域与图像域的信息。实验采用5倍加速度下的二维变分密度采样。在5倍加速条件下，基础的采样时间缩短为172 s。由于不同的方法迭代时间不一致，而ESPIRIT作为传统的压缩感知方法，重建所需时间会大于基于深度学习的方法，而对物理模型的拟合过程也需要少量的时间。总的来说，本研究的方法在重建时间不超过10%的前提下能显著优于其它对比方法。

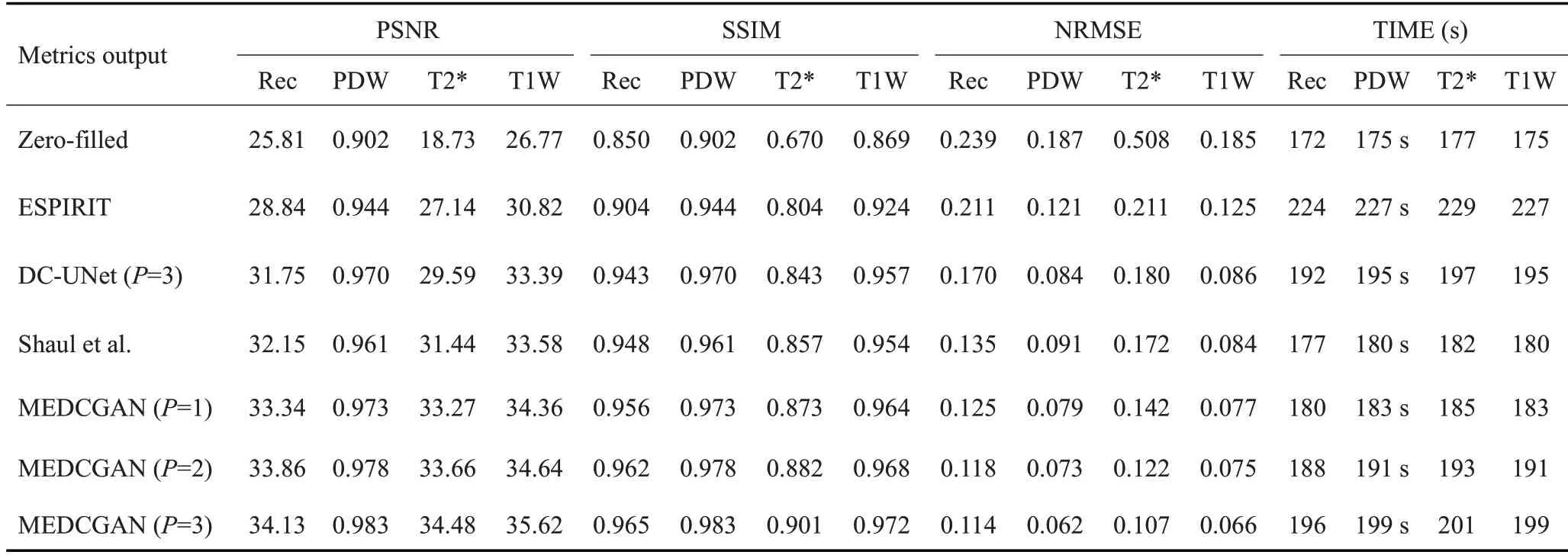
表1 在重建的多回波图像和多对比度图像中进行不同方法实验的比较Tab.1 Comparisons of different methods for reconstructing multi-echo images and multi-contrast images

由于篇幅限制，本研究只展示了2个回波，以及展示了PDW、T1W和定量T2*Map映射下的多对比度图像（图3、4）。综上所述，ME-DCGAN在迭代次数p=3的条件下具有最佳的图像细节恢复表现。

图3 在多回波图像上的5倍变分密度加速下的视觉结果Fig. 3 Results of 5×variable density acceleration of the multi-echo images.

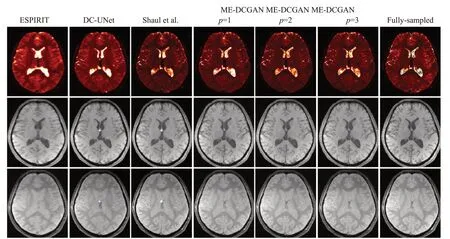
图4 在多参数图像上的5倍变分密度加速下的视觉结果Fig. 4 Results of 5×variable density acceleration of the multi-parametirc maps.

虽然本研究的方法实现了具有竞争力的重建性能，但仍然存在以下问题。首先，组合损失函数的最优权值难以确定。其次，由于物理模型假设“完美”图像质量，容易受到欠采样伪影的影响。表2中的指标均采用了与表1相同的P值计算方法（P＜0.05）。因此通过基于物理模型的最小二乘拟合并不是获得多对比度图像的最佳方法。我们可以利用神经网络来逼近最优参数映射。最后，由于我们使用小的内部数据集，因此需要在更多的数据集上验证方法的有效性。

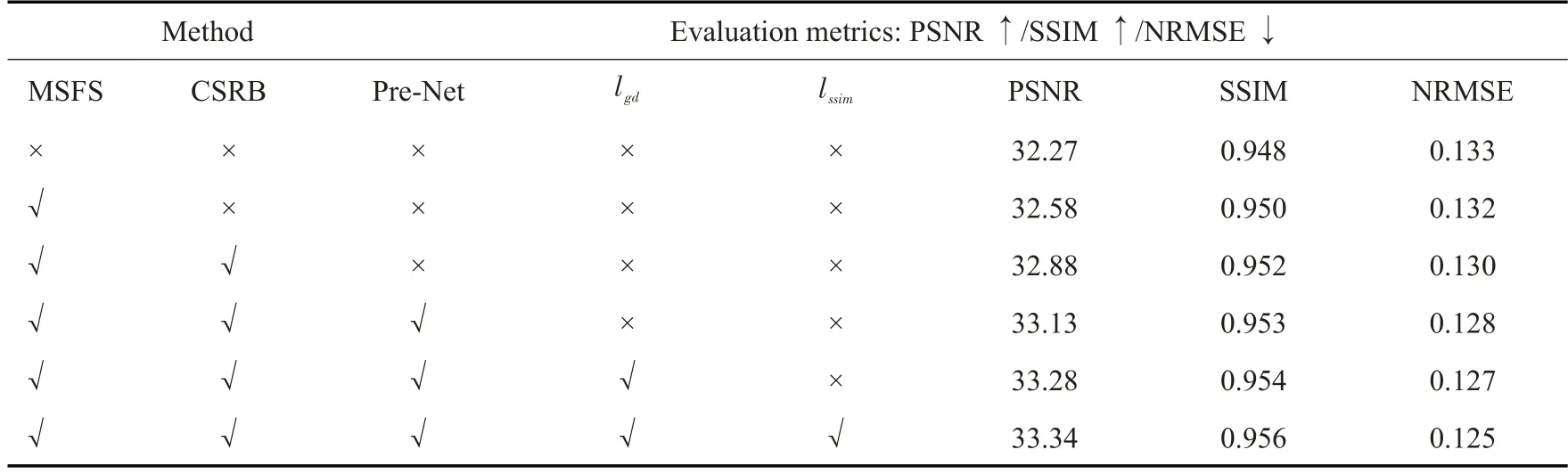
表2 在重建的多回波图像中进行消融实验的比较Tab.2 Ablation experiments of the reconstructed multi-echo images using different methods

而在本研究对不同模块和损失函数评估的消融实验中，本研究将通过实验结果与分析来评估关键组件的有效性。由于篇幅限制，消融实验将在迭代次数p=1并且5倍加速度下的二维变分密度采样条件下比较。表2 展示了引入的模块和损失函数对重建性能的影响。表2表明添加不同损失和不同结构模块均能有效的提高多回波图像的重建质量，并且从指标上的差距可知MSFS和CSRB模块对改善多回波图像重建质量具有最大的帮助。不仅如此，没有任何额外网络结构和损失函数的实验结果也已经超越了DC-UNet和Shaul等的方法，并且随着相应结构和损失函数的增加，本研究的方法均能获得更好的重建指标与实验表现。

3 讨论

近年来，卷积神经网络、生成对抗网络等技术被应用于磁共振重建领域，然而，目前深度学习的重建方法面临许多问题，比如输入数据利用不充分［11,14-20,23-26］、网络结构特异性较差［27］、数据使用形式不符合临床要求［11,13-27,29-32］、损失函数过于简单导致重建图像的质量受到影响［11-24,26,27,29-31］以及数据驱动导致模型拟合能力差［29-32］等问题。对此，本研究提出了一种基于物理模型的级联生成对抗网络的加速定量磁共振成像方法。

在该方法中，针对输入数据只在图像域进行处理的问题，本研究提出了频域、图像域、距离域多域联合学习方法；针对网络结构特异性较差的问题，本研究自适应地优化k 空间生成器和图像生成器结构来增强图像特征信息以获得高质量的重建图像；针对实时性和数据的不正确处理导致的实验与真实场景使用数据形式不一致问题,本研究使用原始的多回波多线圈数据而不是将线圈组合后的数据去训练来加速多对比度多参数磁共振图像重建；针对小数据集和没有使用磁共振物理原理导致的模型拟合能力差的问题，本研究提出了基于物理驱动的深度学习重建方法，通过建立系统矩阵函数而不是直接通过模型端到端训练的方式来增加模型的泛化能力和提高模型性能。总的而言，本研究的贡献如下：本研究使用多回波梯度回波脉冲序列（GRE）信号作为输入，目的是重建多回波图像并生成多对比度多参数图像，这极大地扩展了多回波GRE 在加速磁共振成像上的理论研究基础和应用范围。并且本研究提出了一种基于物理模型的级联生成对抗网络，该网络利用多域信息联合训练以及通过系统矩阵学习图像重建所需的关键参数，并自适应地优化k 空间生成器和图像生成器结构来增强图像特征信息以获得高质量的重建图像。此外，本研究使用原始的多回波多线圈数据而不是将线圈组合后的数据去训练，以确保实验与真实场景使用数据形式一致。最后，本研究提出了一种组合损失函数，并分配适当的损失函数权重以提高图像整体的重建质量。

但是目前基于深度学习的重建方法仍然面临相当大的考验。例如，目前的深度学习方法缺少整体的优化框架，分阶段优化会导致的数据真实性问题。此外，医学图像的标注也是一个严重制约深度学习在核磁共振重建中发展的一个重大因素，所以无监督学习的研究和发展显得格外重要。随着技术的发展，可解释性对于核磁共振重建的成功至关重要，而如何有效地利用深度学习技术来改善其可解释性却仍然是一个棘手的问题，因此，有必要加强相关的研究。

虽然，近几年深度学习在核磁共振重建方法的研究中一直都是热点研究问题，但临床上使用最广泛的还是传统的并行成像方法。深度学习的重建方法在临床应用方面还有待进一步研究，以实现深度学习重建方法在核磁共振扫描仪产品上的广泛落地应用。在未来，我们将充分考虑现有的问题，并且根据其自身特性以及使用场景做了定制，以期望可以推动临床影像的发展。