二次指数平滑多目标组合模型电力负荷预测

吴 迪，马文莉，杨利君

(河北工程大学 信息与电气工程学院，河北 邯郸 056038)

0 引 言

负荷预测是电力部门的重要工作之一[1]。早期短期负荷预测方法有指数平滑法[2]、卡尔曼滤波[3]和自回归积分移动平均值[4]等。

近年来，随着深度学习[5]的高速发展和广泛应用，研究者们提出了RNN[6]和LSTM[7]等模型。文献[8]提出了一种改进RNN和VAR的多变量时间序列预测方法。文献[9]提出了结合指数平滑和RNN的双层混合模型，有助于提升时间序列预测性能。

LSTM在RNN基础上，引入遗忘门、输入门和输出门，更适合学习电力负荷数据的内部变化规律。文献[10]采用贝叶斯优化调整LSTM网络的超参数预测。文献[11]通过分析电价及历史负荷与当前时刻负荷相关性，提出了Attention-LSTM短期负荷预测模型。文献[12]提出了级联LSTM负荷预测模型，从负荷数据周期性和波动性两方面深度预测。

目前，BiLSTM获得广泛应用。文献[13]论证了BiLSTM模型能更好提取负荷数据的双向时序特征。文献[14]提出了Attention-BiLSTM-LSTM组合模型预测方法，仅横向考虑负荷数据的时序性特征，没有纵向考虑负荷数据的周期性特征，进而影响模型预测精度。

针对短期电力负荷预测精度不理想和负荷特征提取不全面的问题，提出一种二次指数平滑多目标组合模型电力负荷预测方法。采用BiLSTM和LSTM串行学习负荷数据的时序性和周期性特征，以获取负荷目标预测值；将二次指数平滑法获得的残差项数据，利用LSTM模型进行训练和迭代，以获取残差目标预测值；将负荷目标预测值与残差目标预测值融合得到修正预测值，实现多目标负荷预测。

1 LSTM电力负荷预测

在短期电力负荷预测中，每天相同时刻电量负荷往往具有相似的变化趋势，即电力负荷具有周期性变化特点，采用LSTM模型3个门结构的设计可以学习电力负荷时间序列中的长短期依赖信息，能更好的提取电力负荷周期性特征。LSTM网络结构如图1所示。

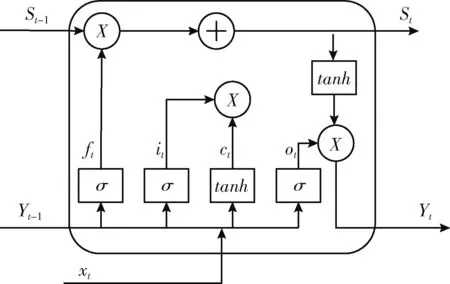
图1 LSTM网络结构

LSTM具体的更新方式如式(1)～式(4)所示。

遗忘门

ft=σ(Wf[ht-1，xt]+bf)

(1)

输入门

{it=σ(Wi[ht-1，xt]+bi)t=tanh(Wc[ht-1，xt]+bc)ct=ft×ct-1+it×t

(2)

输出门

ot=σ(Wo[ht-1，xt]+bo)

(3)

最终输出

ht=ot×tanh(ct)

(4)

式(1)中：ft为遗忘门，Wf是遗忘门的权重矩阵 [ht-1，xt] 表示将两个向量连接成一个更长的向量；bf是遗忘门的偏置项；σ是sigmoid函数。式(2)中：Wi是输入门的权重矩阵；bi是输入门的偏置项。ct为计算当前时刻的单元状态，ct-1为上一次的单元状态，it为输入门。式(3)为计算输出门输出，式(4)最终得到LSTM输出。

虽然LSTM适用于对时序数据建模，但无法实现从后向前的编码。BiLSTM由双向LSTM组合而成[15]，能够更好地捕获负荷数据的双向时序特征。

2 ES-BiLSTM-LSTM多目标组合模型

针对短期电力负荷预测精度不理想及负荷特征提取不全面的问题，本文提出一种二次指数平滑多目标组合模型ES-BiLSTM-LSTM，通过负荷目标预测值与残差目标预测值，实现多目标预测。首先，通过BiLSTM和LSTM模型串行，提取负荷数据的时序特征和周期特征，输出负荷目标预测值；其次，将二次指数平滑法获得的残差项，采用LSTM模型进行迭代训练，提取残差预测值的随机波动性，得到残差目标预测值；最后根据残差项未取绝对值时的正负取值，将负荷目标预测值和残差目标预测值融合，获得修正负荷预测值。ES-BiLSTM-LSTM框架如图2所示。

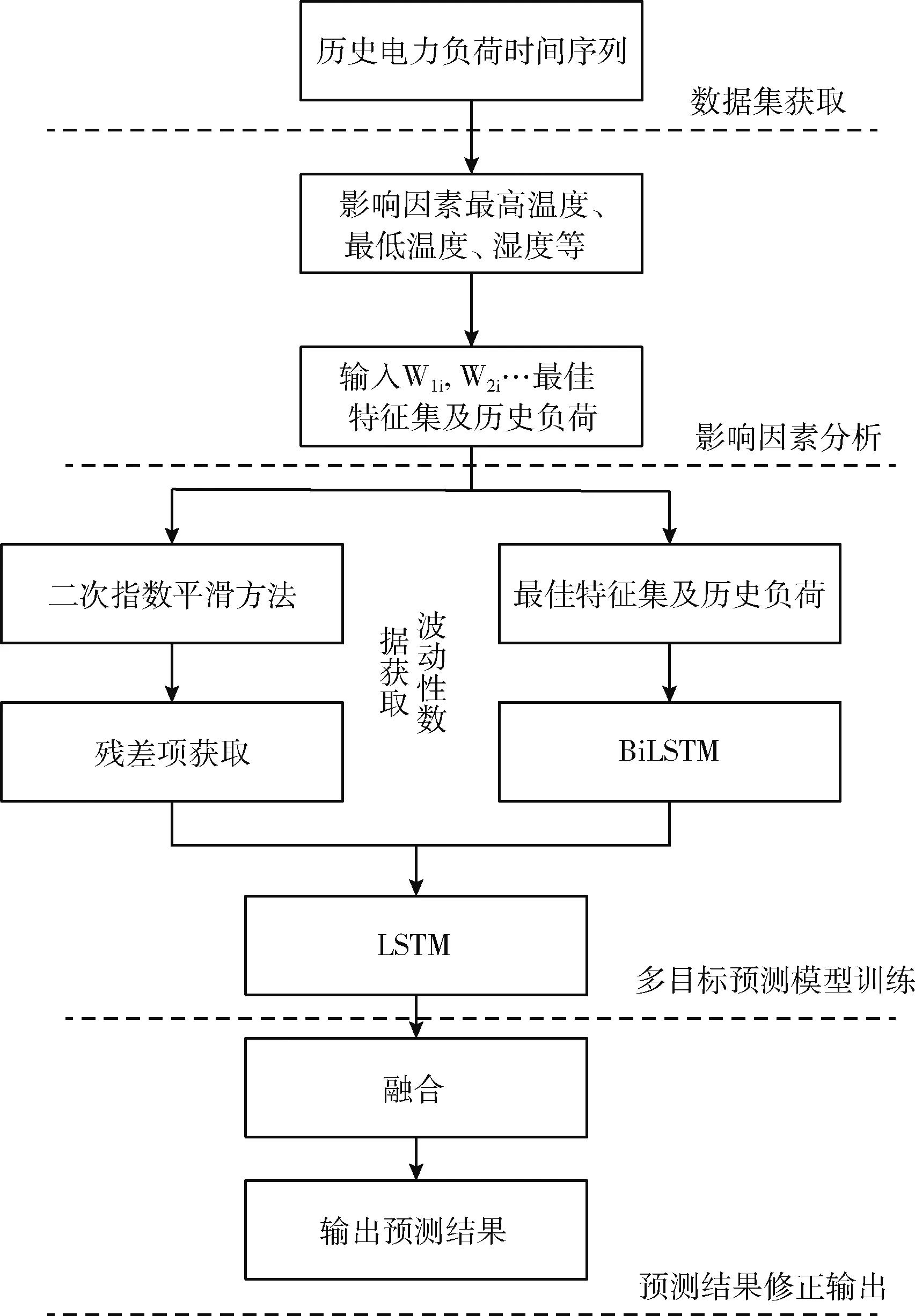
图2 ES-BiLSTM-LSTM框架

如图2所示，ES-BiLSTM-LSTM模型训练过程分为4个阶段，分别是数据集获取阶段、影响因素分析阶段、多目标预测模型训练阶段和预测结果修正输出阶段。

2.1 影响因素分析

针对短期负荷预测受外部环境，如温度、湿度、降雨量等诸多因素影响的问题，本文充分考虑电力负荷数据的最高、最低、平均温度、湿度和降雨量等影响因素，采用Pearson相关系数分析，选取相关性较大的影响因素作为最佳特征集。

Pearson相关系数[16]，用来反映两个变量之间的线性相关程度，如式(5)所示

ρX，Y=E(XY)-E(X)(Y)E(X)2-E2(X)-E(Y)2-E2(Y)

(5)

其中，ρX，Y表示变量X和Y的相关系数，E为数据样本的数学期望。当变量X和变量Y线性不相关时，ρX，Y为0；当变量X，Y负相关时，ρX，Y为-1到0；当变量X，Y是正相关时，ρ为0到1；相关系数的绝对值越大，相关性越强。具体取值见表1。

表1 相关系数范围

依据Pearson相关系数，选出与历史负荷相关性强的影响因素组成最佳特征集S=[W1i，W2i，…，loadi]， 其中，W1i，W2i，…表示经Pearson相关系数选取的与历史负荷数据相关程度高的气象特征变量；loadi表示日负荷量，i=1，2，…t为负荷值的个数。

2.2 多目标预测模型

2.2.1 负荷目标预测训练

针对用户用电行为周期性强，相同时刻电量负荷往往具有相似变化趋势的问题，将最佳特征集及历史负荷数据作为训练集，输入到BiLSTM模型。BiLSTM利用前向和后向两个方向相反的LSTM模型，深层次地提取电力负荷数据集的双向时序特征，增强了模型的表征能力。将BiLSTM模型提取的时序特征输入到LSTM模型中，获取时序数据内部的周期性变化趋势，从而提高电力负荷预测精度。预测结果y={y1，y2，…，yt} 即为负荷目标预测值。周期性模型训练流程如图3所示。

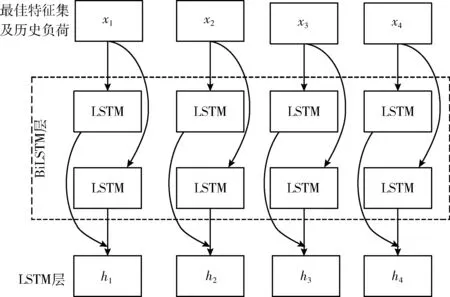
图3 周期性模型训练流程

2.2.2 残差目标预测值训练

由于历史负荷数据及影响因素具有明显隐含周期性和趋势性的变化，一次指数平滑可用于时间序列无明显的趋势变化，但对于趋势变化明显的历史负荷数据，有很大的滞后性。二次指数平滑在一次指数平滑的基础上再平滑，通过对具有线性趋势的负荷数据进行训练，挖掘负荷时间序列曲线的发展规律。本文采用二次指数平滑法平滑处理负荷数据得到预测值。

定义历史负荷数据由t个时间步构成，即时间序列长度为t， 用电量负荷数据序列描述为x={x1，x2，…，xt}， 将该数据序列输入到二次指数平滑模型，二次指数平滑方法公式如下

{St(1)=αxt+(1-α)St-1(1)St(2)=αSt(1)+(1-α)St-1(2)

(6)

在St(1)和St(2)已知的条件下，建立线性趋势预测模型为

{Y^t+T=at+btTat=2St(1)-St(2)bt=α1-α(St(1)-St(2))

(7)

其中，St(1)和St(2)分别为一次指数平滑值和二次指数平滑值，α为平滑系数，反映不同历史时刻数据在指数平滑中所占的权重，且α的值位于[0，1]之间。Y^t+T为第t+T期预测值，T为未来期数的预测。at和bt为模型参数，at为截距，bt为斜率。平滑系数可以通过实验阶段不断调整，选取最佳的平滑系数。

为了提升预测精度，本文将利用二次指数平滑法获得的负荷数据预测值，构成负荷预测序列z={z1，z2，…zt}； 与历史负荷数据x={x1，x2，…，xt} 相减取绝对值，获得残差项。波动性模型训练流程如图4所示。

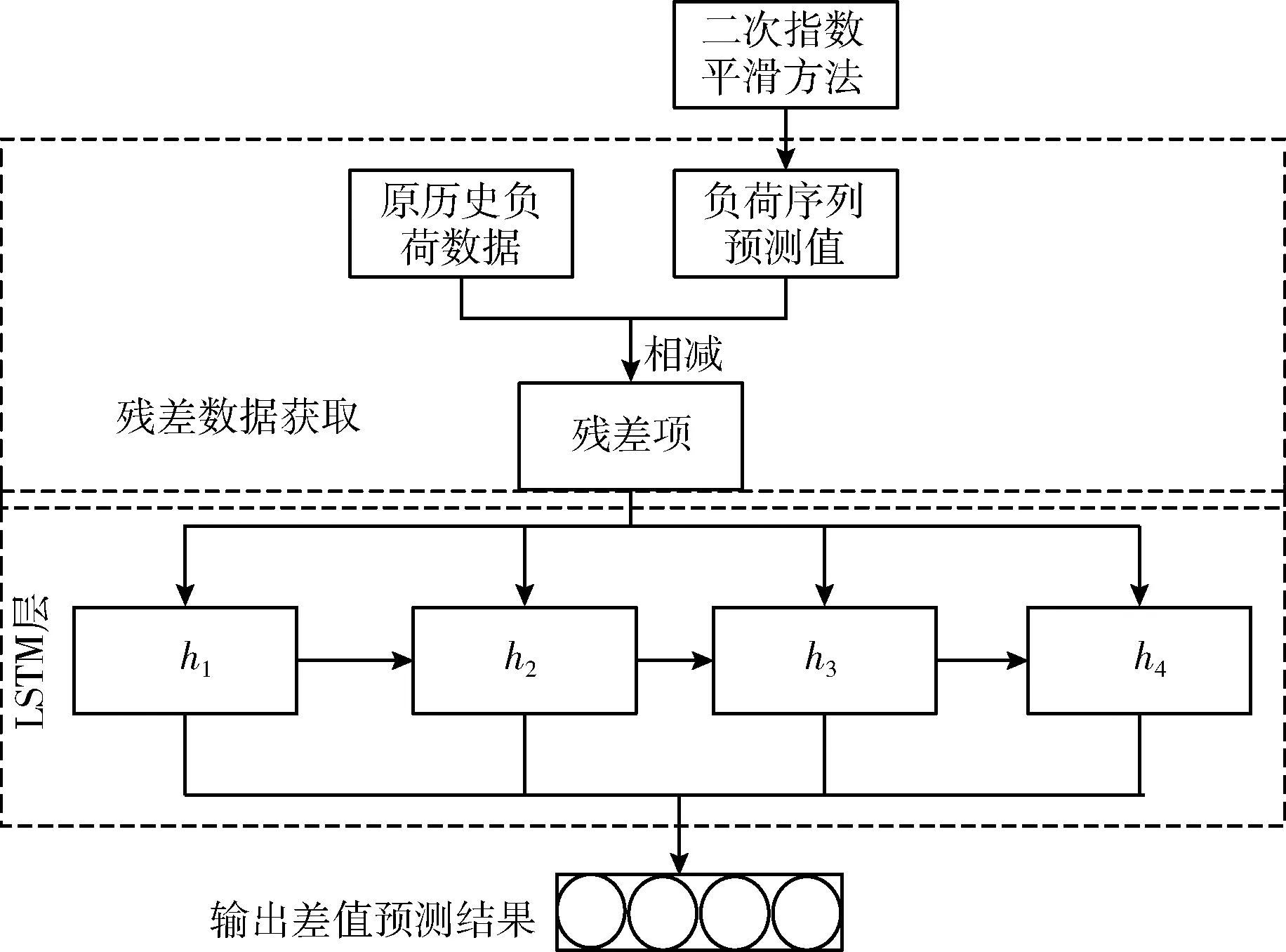
图4 波动性模型训练流程

由于负荷目标预测训练阶段，BiLSTM-LSTM模型提取的负荷特征能力有限，未考虑残差序列对预测结果的影响，以及残差序列之间也存在明显的相关性特征，难以实现精准的预测。

因此，本文利用已存在的负荷目标预测值的误差和残差目标序列相关性的特点，对残差序列利用LSTM模型，进行迭代和训练，学习差值随机性特征的变化规律，实现对负荷预测结果的误差修正，提高预测精度。

2.3 预测结果修正

本文通过负荷目标预测值和残差目标预测值的处理，实现多目标预测。首先利用BiLSTM和LSTM模型串行获得的负荷目标预测值；其次，采用二次指数平滑法和LSTM模型串行提取反归一化后的残差目标预测值；最后将负荷预测值与残差预测值融合，得到修正预测值，反归一化后即为本文预测结果。本文在提取负荷数据特征时，不仅横向考虑了负荷预测周期特征，而且纵向考虑了负荷误差波动特征，提高了预测精度。

由于残差项的训练是取绝对值进行训练，本文采用两种方式对负荷预测值与残差预测值进行融合。一种是将负荷预测值与历史负荷的差值为负时，负荷目标预测值与残差目标预测值求和；另一种是差值为正时，负荷预测值与残差预测值相减。

综上，ES-BiLSTM-LSTM方法描述如下：

输入：历史日负荷数据x={x1，x2，…，xt}、 影响因素(相对湿度、降雨量、最高温度、最低温度、平均温度)

输出：每天的日总负荷量

步骤1 对影响因素做Pearson相关性分析，选出与电力负荷相关性较高的影响因素作为最佳特征集，与历史日总负荷量作为训练集S=[W1i，W2i，…，loadi]；

步骤2 将训练集数据S输入到BiLSTM模型中学习负荷数据的时序特征，再输入到LSTM模型学习时序数据的周期性变化规律；

步骤3 获得BiLSTM-LSTM模型输出的预测结果y={y1，y2，…，yt}；

步骤4 将负荷数据输入到二次指数平滑法的到平稳的负荷预测序列z={z1，z2，…zt}， 将预测值z与实际值x相减取绝对值，得到残差项，输入到LSTM模型学习残差序列的波动性特征；

步骤5 获得残差项训练后的误差波动值r={r1，r2，…，rt}；

步骤6 将步骤3获得的y值与步骤5的r值，按照预测值z与实际值x相减的结果，差值为负时y与r相加，差值为正时y与r相减；

步骤7 取得最后修正后的负荷预测结果。

3 实验结果与分析

3.1 实验环境及数据

本文在64位Windows8版本系统的计算机上进行模型搭建与实验。采用Py Charm 2021.2.1编译器，使用Python3语言，Tensorflow2.6版本的深度学习框架进行实验。

本文采用2016年第九届电工属性建模竞赛试题的A组电力系统短期负荷数据集作为实验数据。数据集为2012年1月1日至2015年1月10日共1100条负荷数据，包括了每天的负荷数据以及对应的影响因素数据(日最高温度、日最低温度、日平均温度、日相对湿度以及日降雨量)。

数据集属性见表2。

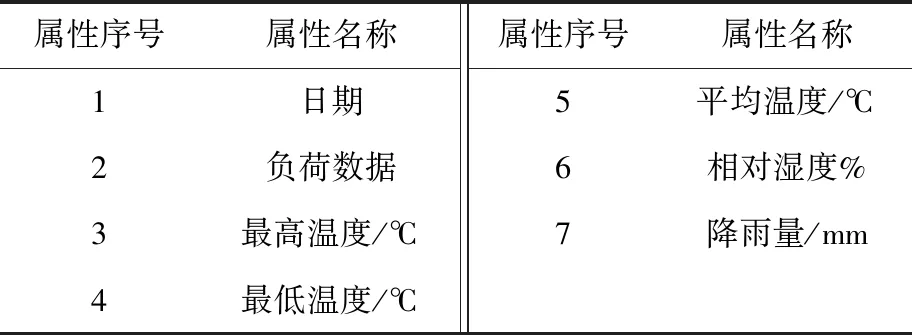
表2 数据集属性

部分数据集属性展示见表3。

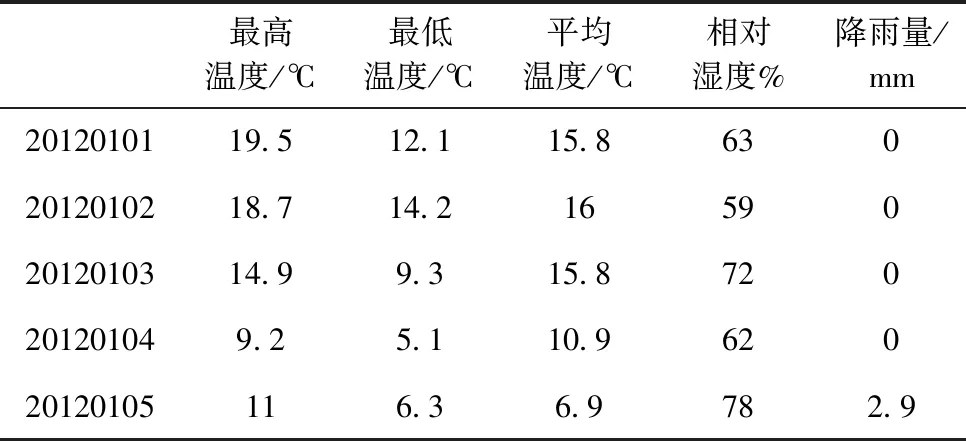
表3 部分数据集展示

3.2 数据归一化处理

为了提升模型训练的效果，本文对电力历史负荷数据、日平均温度和日最低温度等进行归一化处理，将原始数据压缩到0-1之间，计算公式如下

Xi=X-xminxmax-xmin

(8)

其中，X为原始数据，xmax和xmin分别是原始数据中日负荷量(日平均温度、湿度)的最大值和最小值。

3.3 评价指标

本文选用平均绝对误差(mean absolute error，MAE)、均方误差(mean squared error，MSE)和均方根误差(root mean squared error，RMSE)3项指标对模型的精度进行评估，计算公式如下：

MAE的计算公式如下

MAE=1N∑Nn=1|n-yn|

(9)

MSE的计算公式如下

MSE=1N∑Nn=1(n-yn)2

(10)

RMSE的计算公式如下

RMSE=∑Nn=1(n-yn)2N

(11)

式中：N表示为样本的总个数；n和yn分别为预测第n个采样点的实际值和预测值。其中，MAE、MSE和RMSE越小，负荷预测效果越好。

3.4 负荷预测与残差预测分析

对电力负荷数据的影响因素做Pearson相关性分析，选取其中与电力负荷相关性呈强相关的影响因素作为预测模型的输入参数。分析结果见表4。

表4 相关性分析

从表4分析结果中，选取了2个对电力负荷呈强相关的影响因素：最低温度和平均温度。因此实验数据x包括：历史负荷数据、最低温度和平均温度。

本文提出的模型在预测过程分为负荷目标预测值和残差目标预测值，采用BiLSTM-LSTM模型学习负荷数据的周期性特征，获取负荷目标预测值；采用二次指数平滑法-LSTM学习波动性特征，获取残差目标预测值，修正预测结果。

训练过程中BiLSTM和LSTM模型的迭代次数选择如图5和图6所示。

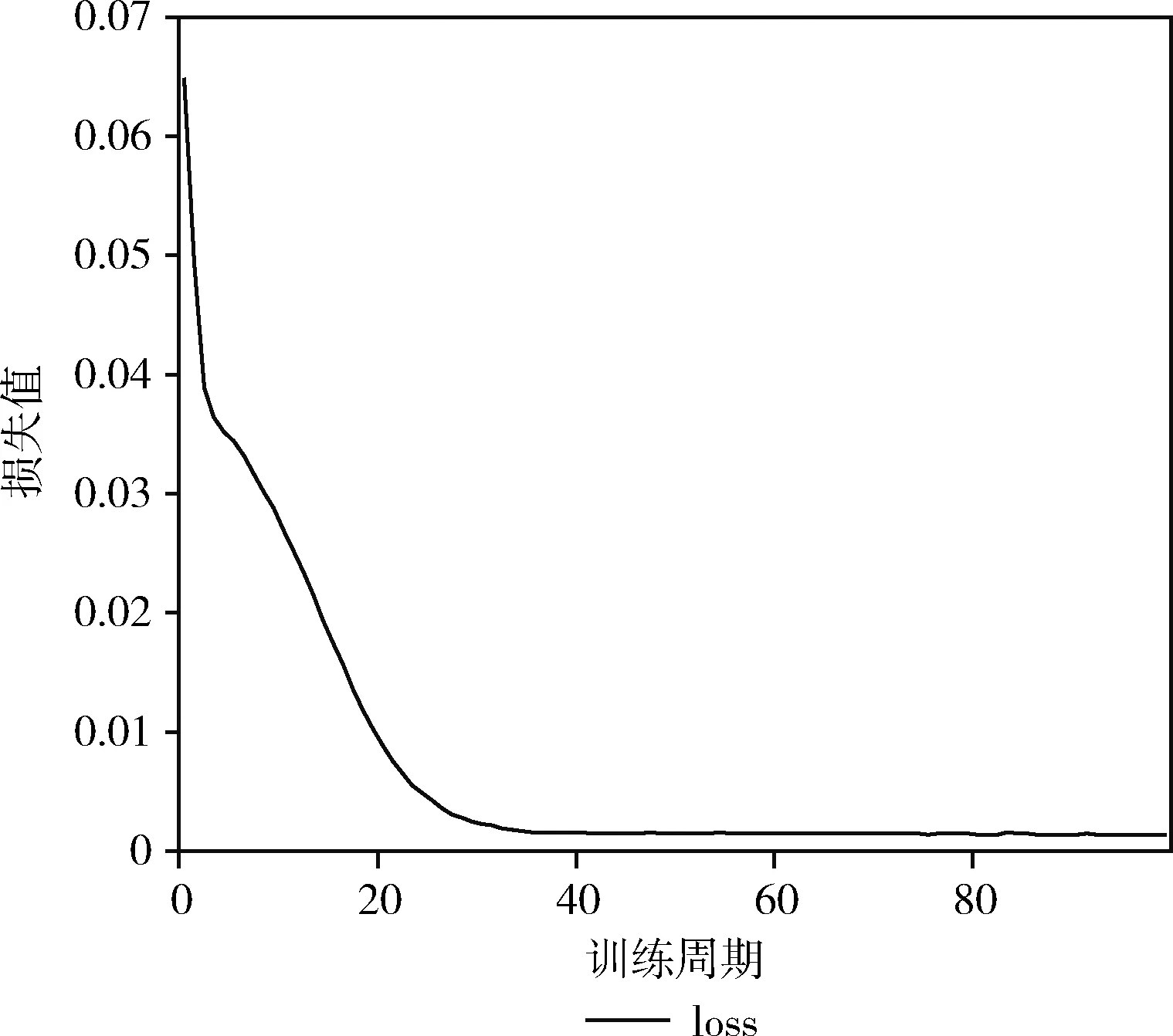
图5 BiLSTM训练过程

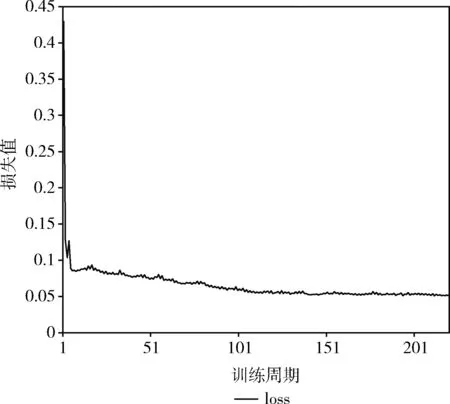
图6 LSTM训练过程

从图5和图6可知，BiLSTM和LSTM在前期的loss波动变化较大，后期趋于平稳。其中，BiLSTM在训练周期达到60，模型收敛；LSTM在训练周期达到200时收敛。

图7为BiLSTM和LSTM模型串行在测试集上的预测效果，其中纵坐标表示预测负荷值归一化后的结果。test表示负荷测试数据，pred表示BiLSTM-LSTM模型的预测结果。从图7中可知，BiLSTM-LSTM模型对于电力负荷需求有着很好的预测效果，但是由于本文是预测日负荷量，数值较大，导致在一些峰值的预测结果上，有一些偏差，所以本文通过对负荷目标预测值与历史负荷值的差值，即残差项的训练来修正预测结果。

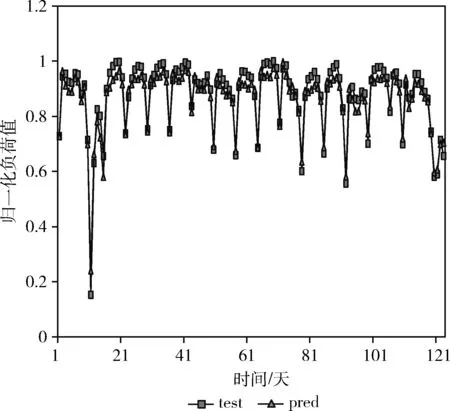
图7 负荷目标预测值与历史负荷对比

图8为二次指数平滑法-LSTM模型在测试集上的预测效果。图8的纵坐标表示残差目标预测值归一化后的结果，其中test表示残差项的测试数据，pred表示经过LSTM模型训练得到的残差项预测值。将通过二次指数平滑法获得的负荷目标预测值与历史负荷值相减取绝对值，得到了残差项。并对其进行训练和迭代，学习残差项的波动性特征，获取残差目标预测值。经过LSTM模型的训练，残差项在个别峰值谷值出现大的偏差。在峰值点，预测偏差最大时，pred值为0.698，test值为0.56；在谷值时，pred值为0.304，test值为0.204。其余各点的残差项预测结果和测试结果是贴近的。这表明模型能够较好提取残差数据的波动性特征。

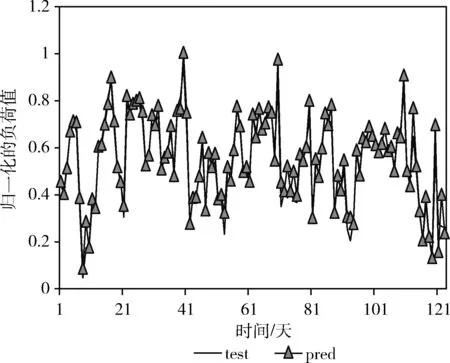
图8 残差目标预测值训练结果

由于日负荷预测，数值较大，BiLSTM-LSTM模型在预测峰值时出现偏差；而通过对残差项的训练，发现误差之间的相关性，可以修正BiLSTM-LSTM模型预测带来的偏差，获得更好的预测结果。

实验中残差项取的是绝对值，将BiLSTM-LSTM模型的预测结果直接与残差项相加，会产生很大偏差，所以本文在预测阶段，将BiLSTM-LSTM模型的预测结果与残差项，按残差项未取绝对值之前的结果，正值相减，负值相加，获得最终的预测结果。

图9展示了负荷目标预测值与残差目标预测值修正后的预测结果，横坐标表示测试集天数，纵坐标表示反归一化后的负荷值。从图9可知，整体的预测效果，比单一BiLSTM-LSTM模型的预测效果更好。残差项的修正过程，使得峰值预测结果的精度有了明显的提高。从图7和图9实验数据峰值的对比结果，可以得出通过对电力负荷数据周期性特征和波动性特征的学习，使得模型的峰值也能够很好的拟合，组合模型的预测值也更符合真实负荷值。

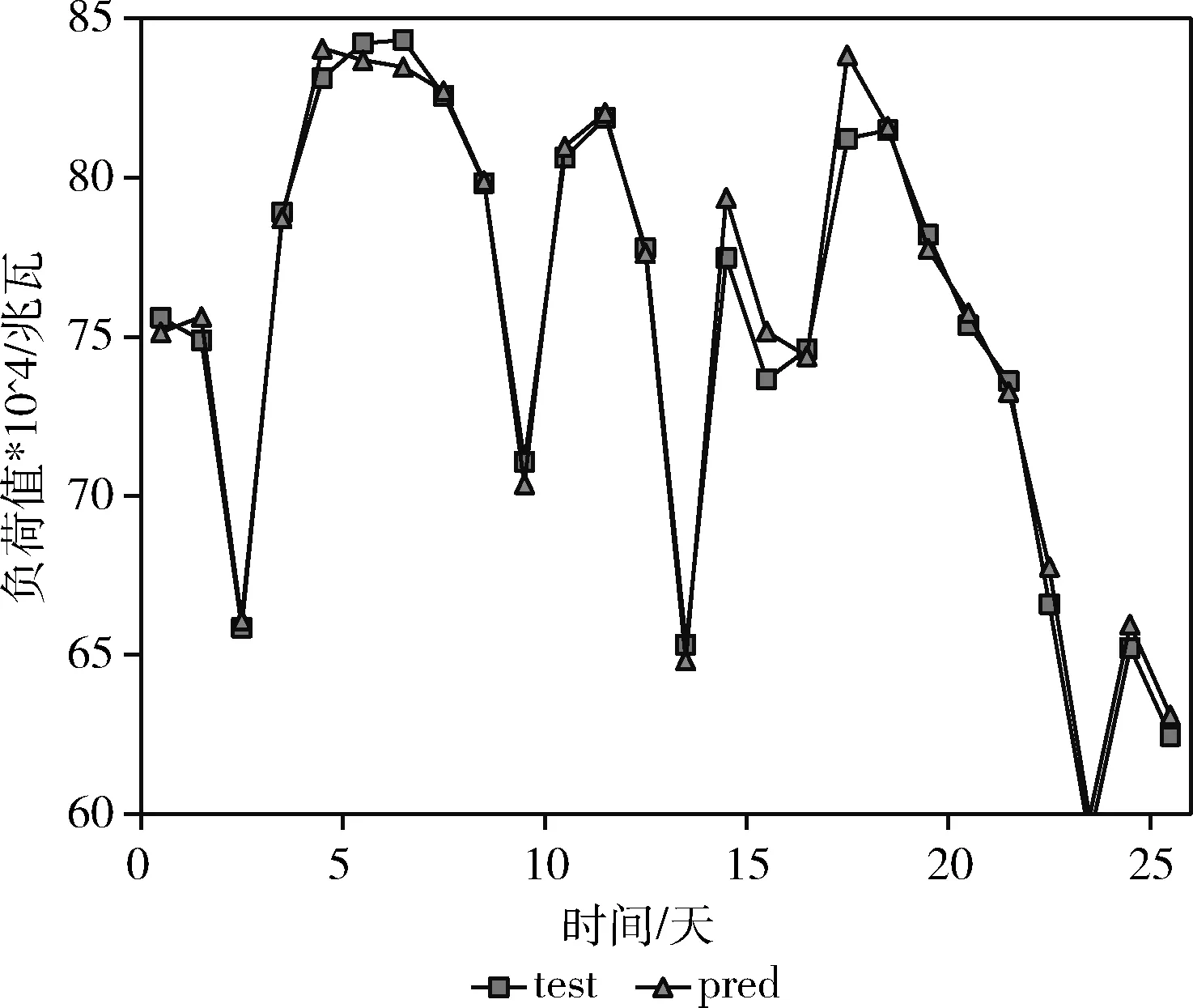
图9 二次指数平滑法多目标组合模型预测结果

3.5 误差指标对比实验

为验证本文提出的二次指数平滑多目标组合模型在电力负荷预测精度方面的优势，与目前经常使用Attention-LSTM神经网络、Attention-BiLSTM-LSTM神经网络、级联LSTM网络模型进行对比。

(1)Attention-LSTM[11]：该模型利用最大信息系数法分析电价与负荷相关性，LSTM利用负荷时序特征，Attention进一步加权，输出预测结果。

(2)Attention-BiLSTM-LSTM[14]：该模型将LSTM和BiLSTM串行，获取负荷数据的双向时序特征及其内部变化规律，并利用注意力机制计算隐层状态不同权重，获得预测结果。

(3)级联LSTM[12]：该模型主要利用LSTM模型将负荷预测分为两个阶段，分别提取电力负荷的周期性和波动性特征。

预测模型对比实验的MAE、MSE和RMSE结果见表5。

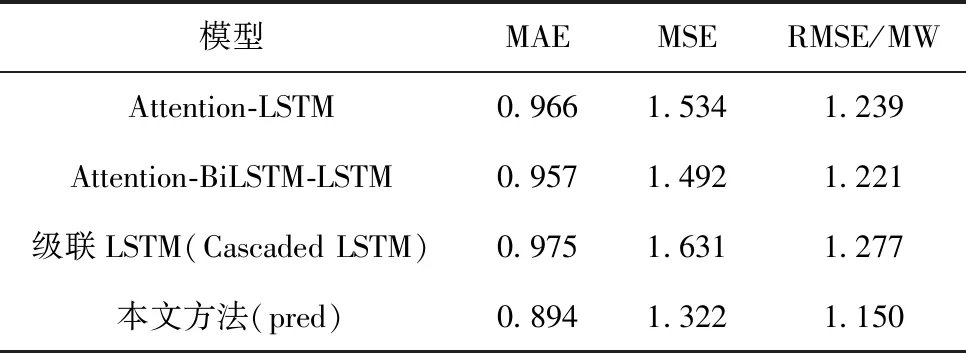
表5 不同模型在多种指标上的预测结果

表5可知，本文提出的方法在MAE、MSE和RMSE等评价指标都表现出较好的性能，分别为0.894，1.322，1.150，即具有最高预测精度。一方面从日负荷预测精度的角度分析，由评价指标可知本文模型预测结果有更高的预测精度，表明了本文方法的有效性和优势。另一方面本文从电力负荷数据中提取时序特征，同时学习差值波动性特征，修正模型预测的误差，获得比较好的预测结果。

不同模型对验证集进行日负荷预测的负荷曲线如图10所示。

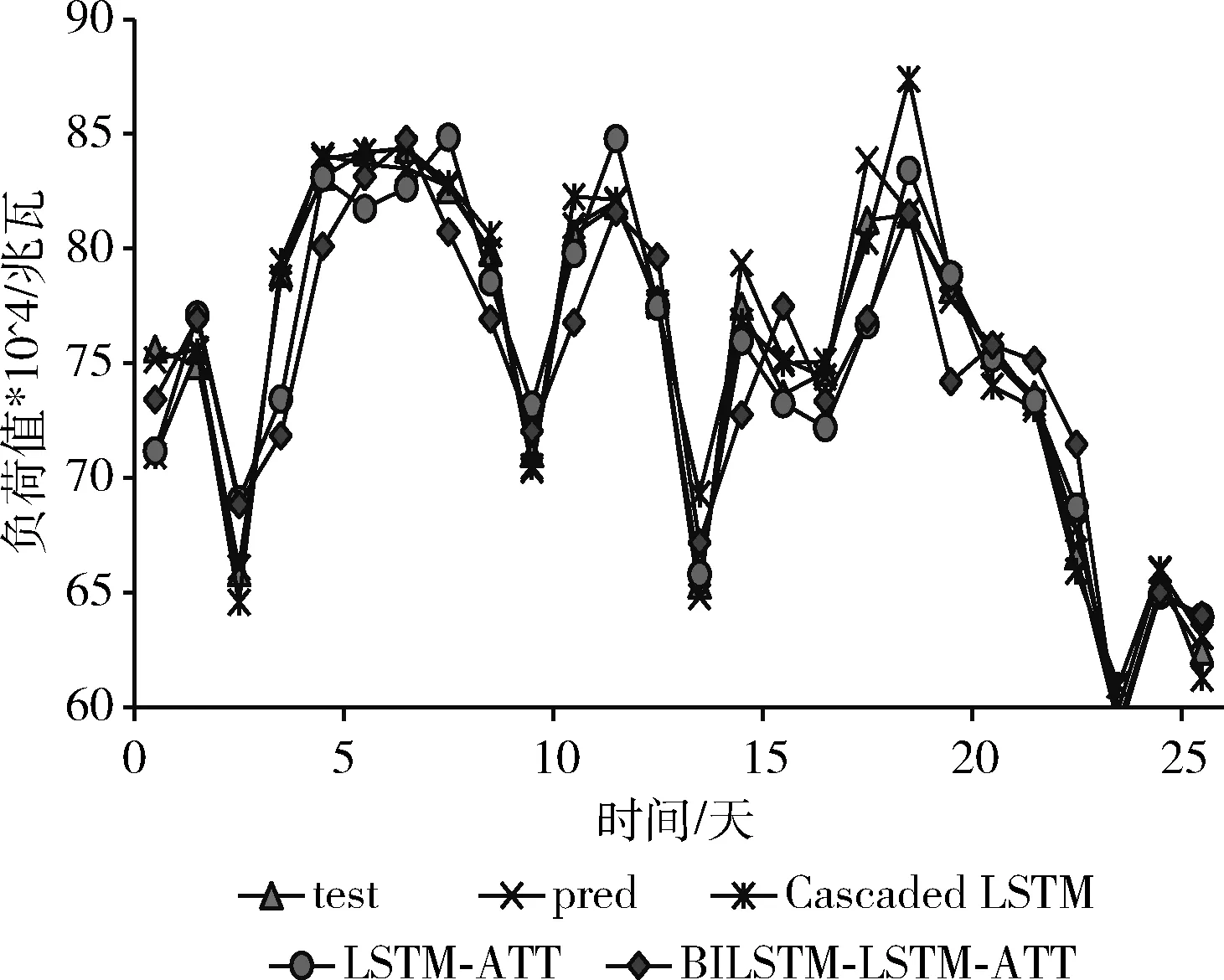
图10 不同模型的电力负荷预测结果

从图10可知，本文提出方法的预测结果pred更加贴近于真实的负荷曲线。体现在预测日总负荷的用电波峰和波谷的总体趋势上，均取得了较好的预测效果。通过对负荷数据时序特征和波动特征的学习，更准确提取了负荷变化的规律。

4 结束语

本文提出了一种二次指数平滑多目标组合模型电力负荷预测方法，利用BiLSTM-LSTM模型提取时序数据的周期性特征，获取负荷数据总体的预测趋势；采用二次指数平滑法-LSTM学习残差序列的随机性特征，预测残差序列内部的相关性规律，提高了ES-BiLSTM-LSTM模型的预测精度；将负荷预测值与残差误差值融合得到修正预测值，实现了多目标负荷预测。实验结果表明，在2016年电工属性建模竞赛试题A组电力系统短期负荷数据集上，本文提出的预测方法，相较于Attention-BiLSTM-LSTM、级联-LSTM、Attention-LSTM和模型，在预测误差指标MAE、MSE和RMSE上均表现出更高的精度。