基于改进SPRT的机载欺骗式干扰检测方法

钟伦珑，刘炅坡，刘永玉，张卓轩

(中国民航大学 智能信号与图像处理天津市重点实验室，天津 300300)

0 引 言

全球导航卫星系统(GNSS)在民用航空领域得到了广泛的应用，但由于GNSS信号微弱且民码结构公开，GNSS导航极易受到欺骗式干扰的影响[1]，对航空安全形成威胁[2]。机载欺骗式干扰检测技术可分为基于信号处理的检测技术[3-5]和基于信息解算[6-8]的检测技术两大类。基于信息解算的检测技术相比于基于信号处理的检测技术无需改变接收机结构，可在区域导航计算机中实现。这种实现方式方便融合其它导航源信息，提高检测性能。

Wald提出的序贯概率比检测(SPRT)算法利用了历史时刻的信息，其对小偏差敏感，广泛应用于故障检测领域中，但是传统SPRT算法检测速度较慢[9]。为加快检测速度，Xiao等[10]提出一种分段SPRT改进方法，减少了历史样本信息的影响，能够在短时延下正确检测故障。在机载导航应用方面，张闯等[11]将SPRT算法应用到组合导航中，将隔离后的滤波结果作为下一时刻的滤波初值辅助故障检测，提高了系统可靠性。基于故障与欺骗产生影响的类似性，研究人员将SPRT技术应用于欺骗式干扰检测。Devaprakash等[12]将GNSS伪距残差作为欺骗检测量，提出一种基于传统SPRT算法的欺骗式干扰检测方法。但由于在欺骗干扰影响下伪距残差会逐渐偏离真实值，导致该方法对伪距欺骗量较小的欺骗式干扰检测性能不佳。

受文献[12]的启发，针对转发式欺骗干扰的机载检测技术，本文通过融合机载多源导航数据构造新的欺骗检测量，并在Bayes最小平均风险条件下计算自适应补偿值，提出一种基于改进SPRT的机载GNSS欺骗式干扰检测方法，并通过实验验证该方法的有效性。

1 基于伪距测量的欺骗式干扰模型

由GNSS基本理论[6]，伪距测量模型如图1所示。

图1 伪距测量模型

载体位置P对应第j颗可见卫星的伪距测量值ρGNSS，j为

ρGNSS，j=rGNSS，j+cδtGNSS-υρ

(1)

其中，rGNSS，j代表载体到第j颗可见卫星的真实距离，cδtGNSS为GNSS接收机钟差导致的位置偏差，δtGNSS表示GNSS接收机时钟误差，c为光速；υρ是包括接收机内部噪声在内的GNSS伪距测量噪声总和，服从零均值的高斯分布，υρ～N(0，σ2GNSS)，σGNSS为伪距测量噪声标准差。

按照干扰生成方式划分，欺骗式干扰可分为转发式和生成式两种。转发式欺骗干扰通过接收可见卫星信号，对其延时和功率放大后转发，导致载体接收机输出错误的定位位置，最终使载体偏离期望航迹。而生成式干扰需要知道载体位置信息，实现难度远大于转发式干扰。因此，对机载转发式欺骗干扰检测技术的研究更为迫切。

根据转发式欺骗干扰的原理，转发式欺骗干扰源通过延时和转发卫星信号引入伪距欺骗量Δρj。伪距欺骗量是指欺骗信号和正常卫星信号解调后得到的伪距测量值的差。干扰源通过改变正常卫星信号的测距码引入伪距欺骗量，从而产生欺骗信号，使得导航设备产生错误的定位结果，实现对导航设备的欺骗。欺骗式干扰影响下的伪距测量模型如图2所示。

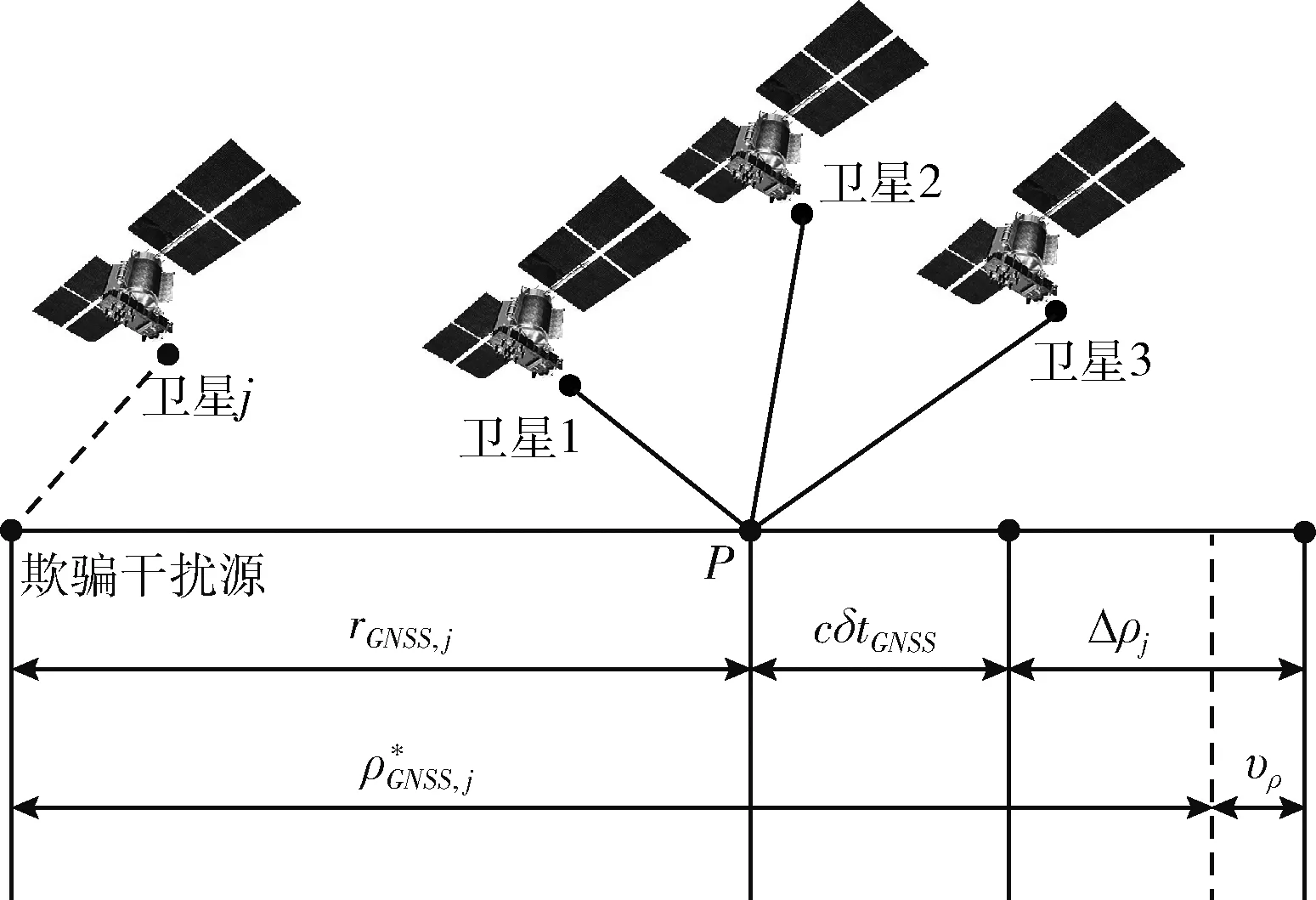
图2 欺骗条件下伪距测量模型

由图可见，存在欺骗式干扰时，受伪距欺骗量的影响，第j颗可见卫星的伪距测量值变为

ρ*GNSS，j=rGNSS，j+cδtGNSS-υρ+Δρj

(2)

2 基于改进SPRT的欺骗式干扰检测方法

2.1 基于改进SPRT的检测方法流程

基于改进SPRT的欺骗式干扰检测方法主要包括基于机载多源数据的欺骗检测量估计和基于SPRT的欺骗式干扰检测两部分。在基于机载多源数据的欺骗检测量估计中，从信息解算层面融合GNSS伪距观测量与其它机载导航源数据估计伪距欺骗量，将其作为欺骗检测量。在基于SPRT的欺骗式干扰检测中，基于Bayes参数估计理论计算欺骗检测统计量的自适应补偿值，提出了一种改进SPRT算法，并应用在欺骗式干扰检测中，加快了欺骗式干扰的检测速度。其具体流程如图3所示。从统计量的计算上分，方法总共包括3步。

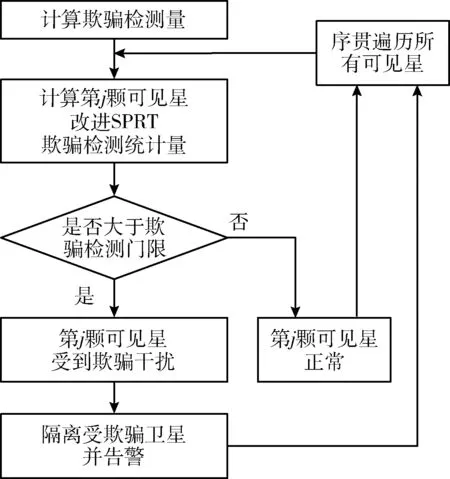
图3 欺骗式干扰检测方法流程

(1)基于机载多源数据计算SPRT欺骗检测量，利用INS、测距机(DME)机载多源数据辅助构建量测方程，并采用加权最小二乘法计算欺骗检测量，具体计算方法如节2.2所述。

(2)在第一步得到的欺骗检测量基础上，基于改进SPRT算法计算第j颗可见卫星的欺骗检测统计量。改进SPRT算法利用欺骗检测量计算欺骗检测统计量的自适应补偿值，构成改进的欺骗检测统计量，具体计算方法如节3.2所述。

(3)将(2)得到第j颗可见卫星的欺骗检测统计量和欺骗检测门限对比，检测第j颗可见卫星是否受到欺骗式干扰：若第j颗可见卫星的欺骗检测统计量大于欺骗检测门限，则判断第j颗可见卫星在当前时刻受到欺骗，隔离第j颗可见卫星并告警；若第j颗可见卫星的欺骗检测统计量小于欺骗检测门限，则判断第j颗可见卫星在当前时刻正常，继续下一颗可见卫星的欺骗检测统计量计算和是否受欺骗式干扰的检测。重复(2)和(3)操作，序贯遍历所有可见卫星，直至检测完成。欺骗检测门限计算方法如节3.2所述。

2.2 基于机载多源数据的欺骗检测量计算

基于SPRT的GNSS欺骗检测方法通常直接采用伪距残差作为检测量[12]。但是，由于现代机载区域导航采用GNSS和INS组合导航的形式[6]，使用GNSS信息对INS进行反馈校正。在欺骗式干扰影响下，被欺骗的GNSS会对INS进行错误的校正[13]，导致伪距残差偏离真实值。在多星受欺骗时，这种情况变得更严重，因此欺骗式干扰检测量不能直接使用伪距残差测量值。针对上述问题，本文结合机载多传感器体制的优势，建立量测方程，利用加权最小二乘法融合不受欺骗影响的DME测量信息，构造新的欺骗检测量，提高多星受欺骗时的检测性能。新的欺骗检测量构造方法如下：

(1)构建所有可见卫星伪距差量测方程

设当前k时刻可见卫星颗数为n，INS推算的载体位置为 (xI，yI，zI)， 卫星星历中第j颗可见卫星位置为 (xSat，j，ySat，j，zSat，j)， 则当前k时刻所有可见卫星伪距估计值为

GNSS，j=(xI-xSat，j)2+(yI-ySat，j)2+(zI-zSat，j)2

(j=1，2，…，n)

(3)

在载体真实位置 (x，y，z) 处对式(3)右侧进行泰勒级数展开，保留一次项误差，可得

GNSS，j=(x-xSat，j)2+(y-ySat，j)2+(z-zSat，j)2+

x-xSat，jrGNSS，jδx+y-ySat，jrGNSS，jδy+z-zSat，jrGNSS，jδz=

rGNSS，j+lGNSS，jδx+mGNSS，jδy+nGNSS，jδz

(4)

其中，rGNSS，j代表载体到第j颗可见卫星的真实距离，lGNSS，j、mGNSS，j、nGNSS，j为载体与第j颗可见卫星几何连线的三维方向余弦，(δx，δy，δz)=(xI-x，yI-y，zI-z) 代表INS推算的载体位置与载体真实位置之间的偏差。

式(4)减去式(1)，可得GNSS伪距差量测方程

δρGNSS，j=GNSS，j-ρGNSS，j=

lGNSS，jδx+mGNSS，jδy+nGNSS，jδz-cδtGNSS+υρ

(5)

其中，δρGNSS，j为第j颗可见卫星的伪距差量测值。

(2)构建测距机斜距差量测方程

设当前k时刻所选的两个DME导航台位置为 (xDME，i，yDME，i，zDME，i)， 利用INS载体位置信息计算DME斜距估计值

DME，i=(xI-xDME，i)2+(yI-yDME，i)2+(zI-zDME，i)2

(i=1，2)

(6)

在载体真实位置 (x，y，z) 处对式(6)右侧进行泰勒级数展开，保留一次项误差，可得

DME，i=(x-xDME，i)2+(y-yDME，i)2+(z-zDME，i)2+

x-xDME，irDME，iδx+y-yDME，irDME，iδy+z-zDME，irDME，iδz=

rDME，i+lDME，iδx+mDME，iδy+nDME，iδz

(7)

其中，rDME，i代表载体到第i个DME导航台的真实距离，lDME，i、mDME，i、nDME，i为载体与第i个DME导航台几何连线的三维方向余弦。

第i个DME导航台斜距测量值dDME，i数学模型为

dDME，i=rDME，i+cδtDME-υd，i

(8)

其中，cδtDME为DME接收机时间误差导致的位置偏差，δtDME表示DME询问器和应答器的总时间误差；υd，i是第i个DME斜距测量噪声，其服从零均值的高斯分布，υd，i～N(0，σ2DME，i)，σDME，i为第i个DME的斜距测量噪声标准差。

式(7)减去式(8)，可得DME斜距差量测方程

δρDME，i=DME，i-dDME，i=

lDME，iδx+mDME，iδy+nDME，iδz-cδtDME+υd，i

(9)

其中，δρDME，i为第i个DME导航台的斜距差量测值。

(3)建立完整量测方程

联立GNSS伪距差量测方程与DME斜距差量测方程，建立量测信息与状态变量之间关系的量测方程

y=Gx+ε

(10)

其中

y=[δρGNSS，1…δρGNSS，nδρDME，1δρDME，2]T；

x=[δxδyδz-cδtGNSS-cδtDME]T；

ε=[υρ…υρυd，1υd，2]T；

G=[lGNSS，1mGNSS，1nGNSS，110

⋮⋮⋮⋮⋮

lGNSS，nmGNSS，nnGNSS，n10

lDME，1mDME，1nDME，101

lDME，2mDME，2nDME，201]

上标T表示矩阵转置。计算矩阵G中的三维方向余弦时，使用INS推算的载体位置 (xI，yI，zI) 替代式(4)和式(7)中的载体真实位置 (x，y，z)。

对式(10)应用最小二乘解算状态变量x时，有以下性质：①没有欺骗式干扰时，状态量x中的位置偏差可有效估计INS的测量误差；②有欺骗式干扰时，由于被欺骗的GNSS对INS进行错误的校正，状态量x中的位置偏差将包含伪距欺骗量。由式(10)，在量测信息y中包含了不受干扰的DME量测信息，可以更准确地解算状态量x。解算得到的状态量又可反过来用于估计所有可见卫星的欺骗检测量。

(4)计算所有可见卫星欺骗检测量

按照国际民用航空组织(ICAO)附件10规定，GNSS伪距测量噪声标准差是定值，而DME的斜距测量噪声标准差与斜距相关，直接对式(10)应用最小二乘估计欺骗检测量时会对欺骗式干扰不敏感。为增强欺骗检测量估计的敏感度，对所建立的量测方程进行噪声标准差归一化处理

Wy=WGx+Wε

(11)

其中

W=[1/σGNSS

⋱

1/σGNSS

1/σDME，1

1/σDME，2]

(12)

与加权最小二乘法在线性回归中的应用类似，通过加权最小二乘法融合不受欺骗式干扰影响的冗余DME导航数据，使得加权最小二乘估计值 (LS)j位于真实伪距欺骗量和被欺骗干扰影响的伪距差量测值 (y)j之间，从而提供更准确的欺骗检测量，提高检测性能。

对式(11)应用最小二乘法[14]，得到所有可见卫星的欺骗检测量

Δj=(LS)j=(G(GTWTWG)-1GTWTWy)j

(j=1，2，…，n)

(13)

可以推得欺骗检测量具有以下性质：①没有欺骗式干扰时，由于伪距差量测值服从零均值高斯分布，欺骗检测量同样服从零均值高斯分布；②有欺骗式干扰时，由于伪距欺骗量的存在，伪距差量测值的均值改变，欺骗检测量服从非零均值的高斯分布。

3 一种基于改进SPRT的欺骗检测统计量算法

3.1 基于SPRT的欺骗检测统计量计算

由接收机自主完好性监视(receiver autonomous integrity monitoring，RAIM)技术[15]和飞机自主完好性监测(aircraft autonomous integrity monitoring，AAIM)技术[16]发展而来的RAIM欺骗检测方法和AAIM欺骗检测方法基于卡方检验思想，将当前时刻所有可见卫星欺骗检测量的平方和作为欺骗检测统计量，没有利用历史信息，导致伪距欺骗量较小时，欺骗式干扰检测率低[17]。SPRT算法基于二元假设下条件概率的对数似然比，利用欺骗检测量的当前和历史信息计算欺骗检测统计量，可提高欺骗检测率。

以式(13)得到的第j颗可见卫星欺骗检测量Δj为输入，作为SPRT算法当前k时刻的观测样本fk，j， 则历史时刻到当前k时刻的第j颗可见卫星的欺骗检测量构成一组观测样本 {ft，j|t=1，2，…k}。 这组样本的样本均值k，j和方差σ2k，j的当前值为

k，j=1k∑kt=1ft，j，σ2k，j=1k∑kt=1(ft-k，j)2

(14)

基于二元假设检验[8]，定义原假设H0：第j颗可见卫星未受欺骗，ft，j(t=k)=0； 备择假设H1：第j颗可见卫星受欺骗，ft，j(t=k)=k，j。

在二元假设的条件下，观测样本ft，j的条件概率密度函数可表示为

p(ft，j|H0)=12πσk，jexp[-f2t，j2σ2k，j]

(15)

p(ft，j|H1)=12πσk，jexp[-(ft，j-k，j)22σ2k，j]

(16)

欺骗检测统计量的当前值λk，j可表示为历史时刻到当前k时刻的对数似然比Zt，j(t=1，2，…，k) 之和，即

λk，j=Z1，jZ2，j…Zk，j=

lnp(f1，j|H1)p(f2，j|H1)…p(fk，j|H1)p(f1，j|H0)p(f2，j|H0)…p(fk，j|H0)=

ln{exp[∑kt=1f2t，j-(ft，j-k，j)22σ2k，j]}=k2k，j2σ2k，j

(17)

式(14)中，当前k时刻的样本均值k，j和方差σ2k，j由前一时刻的样本均值k-1，j和方差σ2k-1，j递推得到

{k，j=k-1kk-1，j+1kfk，jσ2k，j=σ2k-1，j+k-1k(k-1，j-k，j)2

(18)

3.2 改进SPRT算法

当伪距欺骗量较小时，由式(17)可知，SPRT欺骗检测统计量λk，j需较长时间才能大于欺骗检测门限，导致检测时间过长，难以满足实时告警的需求。

针对这一问题，本文应用Bayes参数估计理论，提出一种自适应SPRT改进算法。综合考虑虚警风险、每次采样所付出的风险和当前k时刻欺骗检测量的大小，在Bayes平均风险最小条件下，计算式(17)的SPRT欺骗检测统计量的自适应补偿值，加快欺骗检测速度。

设原假设H0的先验概率为π0，备择假设H1的先验概率为π1(π0+π1=1)。H0为真，预期采样次数为N0；H1为真，预期采样次数为N1；每次采样所付出的风险为r。H0为真但接受H1所产生的虚警风险为K1，虚警率为α；H1为真但接受H0所产生的漏警风险为K0，漏警率为β。

根据Bayes参数估计理论[18]，当H0为真时，所付出的Bayes平均风险R0为

R0=αK1+rN0

(19)

当H1为真时，所付出的Bayes平均风险R1为

R1=βK0+rN1

(20)

由上述两式，总Bayes平均风险R为

R=π0(αK1+rN0)+π1(βK0+rN1)

(21)

在传统SPRT算法中，预期采样次数N0和N1由预设的虚警率α和漏警率β、当前k时刻的对数似然比的期望值EH1(Zk，j) 和EH0(Zk，j) 计算得来

N0=(1-α)ln(β1-α)+αln(1-βα)EH0(Zk，j)

(22)

N1=βln(β1-α)+(1-β)ln(1-βα)EH1(Zk，j)

(23)

此外，可以推导出传统SPRT算法的上门限lnA、下门限lnB[19]和虚警率α、漏警率β的关系式为

α=1-BA-B、β=B(A-1)A-B

(24)

按照机载GNSS接收机性能要求规范[16]，虚警率α和漏警率β规定值接近于0，且α≪β，此时式(22)、式(23)、式(24)可近似为

{N0≈lnBEH0(Zk，j)、N1≈lnAEH1(Zk，j)

α≈1A、β≈B

(25)

将式(25)代入式(21)可得当前k时刻总Bayes平均风险Rk的表达式

Rk=π0(1AK1+rlnBEH0(Zk，j))+π1(BK0+rlnAEH1(Zk，j))

(26)

式(26)相对于A求偏导，并令其偏导为零，即可得到使总Bayes平均风险最小的Ak

Ak=π0K1EH1(Zk，j)rπ1

(27)

可以认为第j颗可见卫星是否受欺骗干扰的先验概率是相等的，即π0=π1，代入式(27)，将Ak的对数作为自适应补偿值ζk，j

ζk，j=lnK1EH1(Zk，j)r

(28)

其中，比值r/K1代表对欺骗干扰施加欺骗量的敏感程度。在机载GNSS完好性监视的工程应用中，虚警产生的风险比每进行一次采样引起的风险要大，可设r与K1有0.5倍的关系，即比值r/K1=0.5。EH1(Zk，j) 为第j颗可见卫星受欺骗时对数似然比的期望值

EH1(Zk，j)=E[lnexp[-(fk，j-k，j)22σ2k，j]exp[-f2k，j2σ2k，j]|H1]=

E[2fk，jk，j-2k，j2σ2k，j|ft，j(t=k)=k，j]=2k，j2σ2k，j

(29)

EH1(Zk，j) 的大小随欺骗干扰加入的伪距欺骗量变化，因此补偿值ζk，j的大小也将随伪距欺骗量而变化，可实现对检测统计量λk，j的自适应补偿，减小达到检测门限的时间。

在各个采样时刻，由式(28)补偿式(17)的统计量，可得基于本文改进SPRT算法的第j颗可见卫星欺骗检测统计量λ*k，j

λ*k，j=λk，j+∑kt=1ζt，j

(30)

写成递推形式为

λ*k，j=λ*k-1，j+Zk，j+ζk，j

(31)

与一般SPRT相同，检测门限Tρ由虚警率α和漏警率β计算得到

Tρ=lnA=ln1-βα

(32)

4 仿真实验与分析

4.1 实验设置和评价指标

在实验室的机载导航系统仿真平台中嵌入本文的欺骗式干扰检测方式，在飞机巡航阶段中模拟不同欺骗情形，进行蒙特卡洛仿真，统计欺骗检测率，分析欺骗式干扰检测性能。

按照ICAO附件10标准规定[20]，仿真实验相关参数设置见表1。

表1 仿真参数

表1中，Li为飞机到第i个DME导航台的斜距，计算时使用式(6)得到的DME斜距估计值DME，i代替Li。由表1中虚警率和漏警率值，通过式(32)计算可得欺骗检测门限为Tρ=11.5119。

为模拟可见卫星数较少和伪距欺骗量较小的情形，将卫星遮蔽角设为30°，并在模拟飞机巡航阶段航迹中，保持可见卫星数为5颗，伪距欺骗量范围为10 m到55 m。模拟不同颗数卫星受欺骗，欺骗场景设置见表2。

表2 欺骗场景设置

在每个欺骗场景中，以5 m为间隔，对受欺骗卫星依次

施加10 m到55 m范围内的伪距欺骗量，每个伪距欺骗量下进行2000次蒙特卡洛实验，计算欺骗检测率Pd

Pd=Num[λ*k，j>Tρ，td≤30]q

(33)

其中，q为蒙特卡洛实验次数，td为检测时间，Num[λ*j>Tρ，td≤30] 表示成功检测的次数。

评价指标欺骗检测率Pd的选用参照ICAO附件10对机载设备巡航阶段的完好性要求。机载导航设备在受到欺骗式干扰的30 s内的最大漏警率不能超过0.001，即在受到欺骗的30 s内需具有99.9%以上的概率检测出欺骗的存在。基于此，选用在加入欺骗式干扰后的30 s内成功检测的次数与总蒙特卡洛实验次数的比值作为评价指标Pd。

将加入欺骗式干扰后的30 s内检测统计量超过阈值的记为一次成功检测。在告警时间要求下的欺骗检测率Pd的可综合反映欺骗检测速度和检测精度，表征欺骗检测性能。

4.2 检测结果分析

(1)欺骗检测率

在不同欺骗场景下，基于改进SPRT的机载GNSS欺骗式干扰检测方法的欺骗检测率Pd随伪距欺骗量的变化曲线如图4所示。

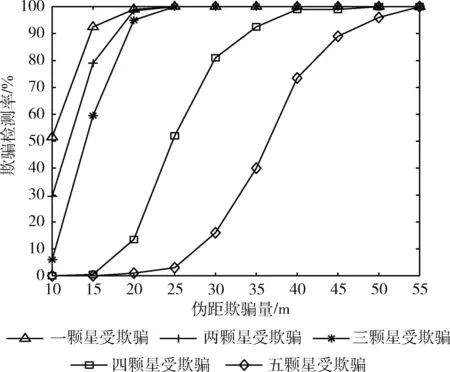
图4 不同欺骗场景下欺骗检测率变化曲线

由图4可见，同一欺骗场景下，本文方法的欺骗检测率随着伪距欺骗量的增加而增大，并逐渐收敛到100%。同一伪距欺骗量，不同欺骗场景下，欺骗检测率随着受欺骗卫星数的增加而变小。

随着受欺骗的卫星数增加，GNSS对INS错误的反馈校正会更严重，导致同一伪距欺骗量下，欺骗检测率会随受欺骗的卫星数增加而变小。由于四、五颗星受欺骗时，受欺骗卫星数大于未受欺骗卫星数加两个DME伪卫星数，相当于从真实卫星占优场景转变到受欺骗卫星占优场景，导致了四、五颗星受欺骗和一、二、三颗星受欺骗相比，欺骗检测率的收敛速度变慢。

包括五颗星全都受欺骗的情况在内，在加入的伪距欺骗量达到55 m时，本文方法的欺骗检测率收敛到100%，表明不管少星受欺骗情况还是多星受欺骗，尽管伪距欺骗量较小，本文方法都可达到较好的检测性能。

(2)欺骗检测时间

在3颗卫星受欺骗场景下，施加5 m伪距欺骗量，使用节2.2方法计算的欺骗检测量进行欺骗检测，SPRT算法和本文改进SPRT算法的检测统计量随时间的变化曲线如图5所示。

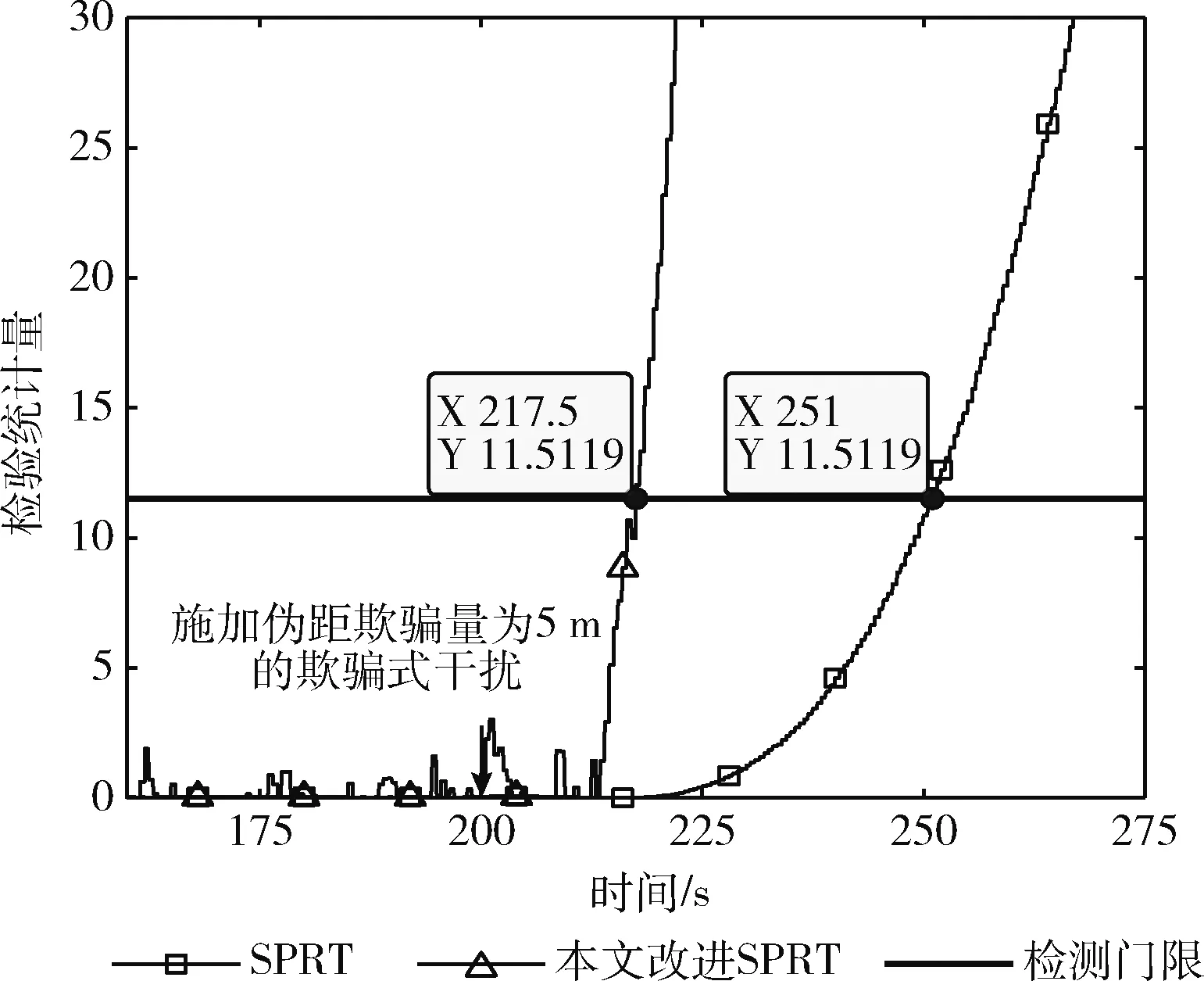
图5 SPRT和本文改进SPRT检测时间比较

由图5可见，在第200 s加入欺骗之前，本文改进SPRT欺骗检测统计量存在小幅波动，这是由于伪距测量噪声的存在造成的。改进SPRT算法中的补偿值根据当前检测量大小自适应改变，不会因噪声的存在形成较大补偿而导致检测统计量超过门限产生虚警。在200 s加入欺骗后，本文改进SPRT欺骗检测统计量在17.5 s后达到检测门限，而SPRT欺骗检测统计量在51 s后才达到检测门限。可见，本文改进SPRT算法大大加快了检测速度，同时没有产生虚警。

表3是在可见星为5颗，不同卫星受欺骗场景下，施加5 m伪距欺骗量，SPRT算法和本文改进SPRT算法的欺骗检测时间。

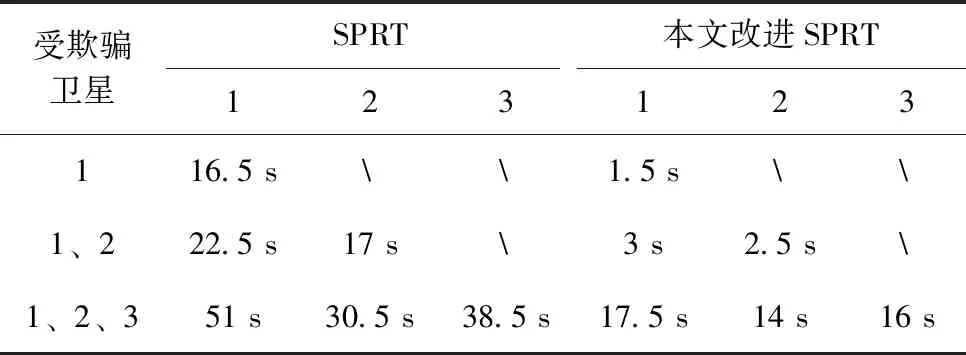
表3 不同欺骗场景下的检测时间对比

从表3可以看出，在相同的欺骗场景下，改进SPRT算法的检测时间远快于SPRT算法，自适应补偿值能有效加快算法检测速度。在3颗星受欺骗时，SPRT算法的检测时间超过30 s，不满足机载设备巡航阶段30 m告警时间要求，而改进SPRT算法检测速度更快能够满足。随着受欺骗卫星数的增加，SPRT算法和本文改进SPRT算法检测速度变慢，这是由于INS受到错误的反馈校正更严重，欺骗检测量会在一定程度上偏离真实值，导致欺骗检测统计量超过阈值的时间增加。

本文改进SPRT算法检测速度更快，这是因为SPRT算法是根据历史时刻信息和当前时刻信息递推计算欺骗检测统计量，当受欺骗后其欺骗检测统计量会被未受欺骗时的历史时刻信息影响，导致其欺骗检测统计量超过阈值的时间较长，而改进SPRT算法的自适应补偿值根据当前时刻信息对欺骗检测统计量进行补偿，使得欺骗检测统计量更快的超过阈值，加快了检测速度。

4.3 检测性能对比

通过在机载导航系统仿真平台中实现RAIM和AAIM检测方法，进行对比实验，验证融合DME、INS冗余多源数据和加入改进SPRT算法对欺骗检测性能的影响。

RAIM方法的本质是对GNSS的冗余观测量进行一致性校验，导致RAIM方法的可用性受限于可见卫星冗余数，不能处理可见卫星数目较少、或异常卫星数目占多的情形[21]。除了GNSS观测量，AAIM算法还利用气压高度表[22]、惯性导航系统(INS)[23]等其它机载导航源提供的冗余测量信息进行一致性校验，相比RAIM方法，降低了对可见卫星数目的要求，但异常卫星数目增多时检测性能同样急剧下降。此外，RAIM和AAIM方法对小伪距欺骗量的检测率较低[24]。

具体地，实验中对比的是基于最小二乘的RAIM方法，以及融合INS和DME冗余多源数据的AAIM算法。本文方法同样融合了DME、INS冗余多源数据，但与AAIM方法相比利用了本文所提出的改进SPRT算法计算欺骗检测统计量。

由于在可见卫星为5颗时，RAIM算法只能对单星受欺骗的情况进行检测。设置了可见卫星为5颗且单颗星受欺骗的场景进行对比实验。

本文算法、RAIM和AAIM算法在可见卫星数为5且单颗星受欺骗时，欺骗检测率随伪距欺骗量的变化曲线如图6所示。

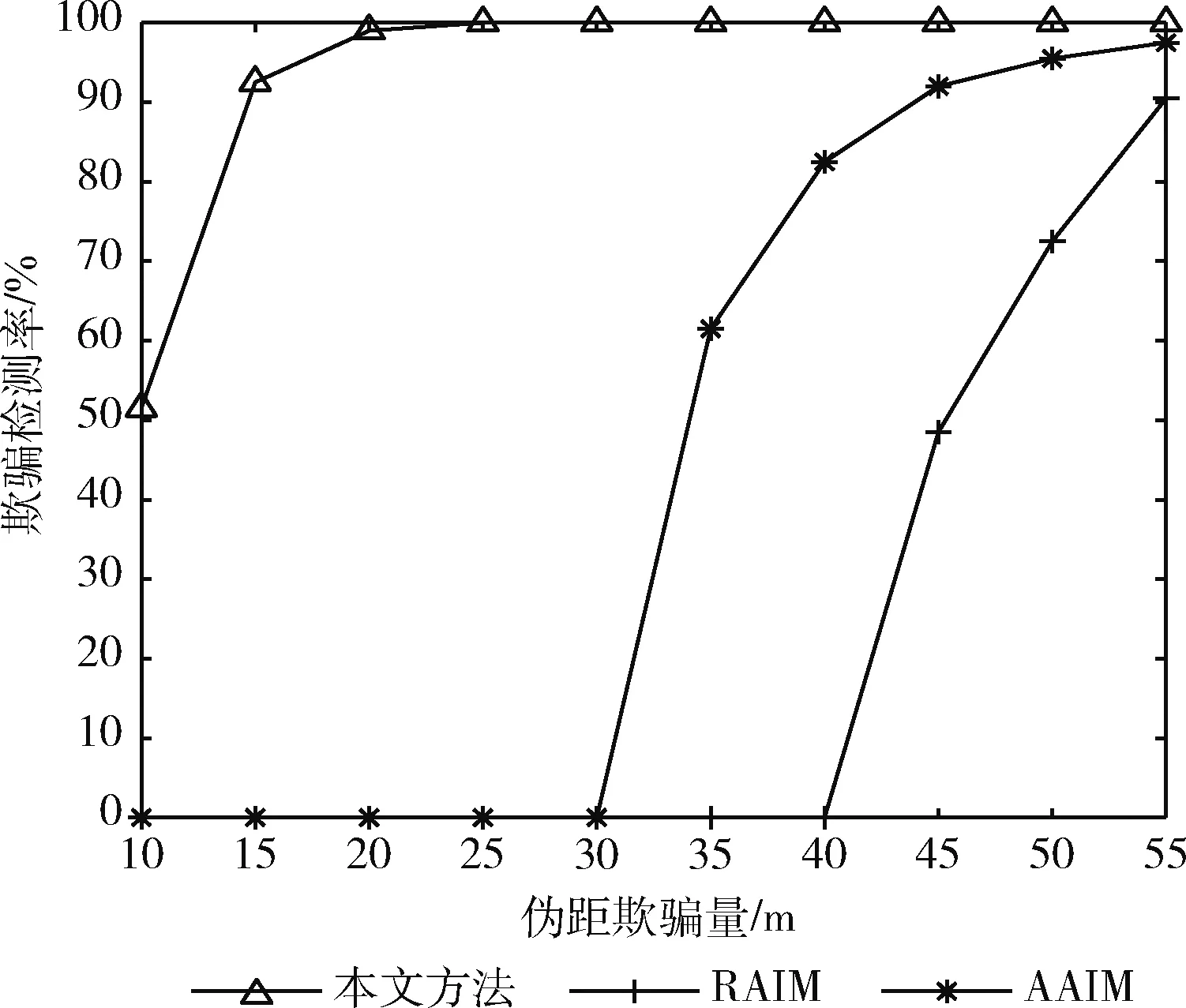
图6 欺骗式干扰检测算法对比

由图6可见，本文方法在较小的10 m到55 m伪距欺骗量下的欺骗检测率明显优于RAIM算法和AAIM算法，25 m伪距欺骗量时本文方法的欺骗检测率已经收敛到100%，而RAIM算法和AAIM算法在55 m伪距欺骗量时欺骗检测率尚未收敛到100%。表明在伪距欺骗量较小时，与传统RAIM算法和AAIM算法相比，本文方法依然能够效地检测欺骗式干扰，并且欺骗检测率的收敛速度也要快于RAIM算法和AAIM算法。

这是由于本文方法融合DME、INS冗余多源数据计算欺骗检测量，使其更接近真实值，并且应用了本文提出的基于改进SPRT的欺骗式干扰检测算法，使欺骗检测统计量对小伪距欺骗量灵敏度更高，提高了其在小伪距欺骗量下的检测性能。

5 结束语

本文通过融合INS和DME机载多源数据，结合Bayes参数估计理论，提出了一种适用于多星受欺骗场景并对小伪距欺骗量敏感的GNSS欺骗式干扰检测方法。实验结果表明，本文方法在保证检测速度满足告警时间要求的前提下，在多星受欺骗和伪距欺骗量较小情况均具有较高的欺骗检测率。在Bayes平均风险最小条件下，计算自适应补偿值，在不产生额外虚警的情况下加快了欺骗检测速度。与现有RAIM和AAIM算法相比，对于隐蔽性强的小伪距欺骗，本文方法体现出了更好的检测性能。