参数不确定条件下的油气站场安全完整性等级验证方法
2023-09-12施昊彤
施昊彤
(国家管网集团建设项目管理分公司 西四线新疆工程项目部,新疆 哈密 839000)
油气管道和站场是完整性管理的重要组成部分,随着管理者和公众对于站场内工艺流程过程安全的日益重视,安全仪表系统(SIS)的应用也越来越多[1-2]。GB 50251—2015《输气管道工程设计规范》中给出了管道监控系统、仪表自控系统的一般性规定[3],但没有指明SIS的使用范围和使用方法。IEC 61508和IEC 61511将安全生命周期定义为分析阶段、实施阶段和运行阶段,并指出为保证重要工艺流程的正常生产,应设置由传感器、逻辑控制器和执行机构组成的SIS。对于SIS需要硬件配置与之相适应的可靠性水平,即完整性等级(SIL)[4-6]。其中,SIL等级的验证结果可确定现有的安全仪表回路是否满足要求,并针对性地改进不满足要求的回路,提出风险降低、风险减缓措施,对于油气站场的安全运行具有重要意义。但SIL验证中涉及较多的评估模型简化和参数假设,使评估结果与现场实际相差较多,且可靠性框图、故障树和马尔科夫链等评价方法中均采用精确的失效参数进行计算,这无疑无法表征失效数据不充分、失效模式未被识别等客观因素[7]。综上所述,在分析SIL验证不确定性因素的基础上,分别利用蒙特卡洛和模糊理论建立参数概率分布已知、参数概率分布未知等两种情况下的SIL验证流程,并从置信度、合规性概率的角度分别评价两种方法,以期减少数据缺乏条件等不确定性因素对SIL验证结果的影响。
1 SIL验证模型及不确定性因素
1.1 SIL验证模型
石油化工行业中安全相关系统普遍执行低要求操作模式,即要求动作频率不大于1次/a,采用安全功能平均要求失效概率(PFD)衡量SIL等级[8]。以“MooN”(M≤N)型表示N个独立完成相同功能的通道中有M个通道完好,IEC 61508-6: 2010Functionalsafetyofelectrical/etectronic/programmableelectronicsafety-relatedsystems-Part6:GuidelinesontheapplicationofIEC 61508-2 and IEC 61508-3中给出了常见硬件冗余结构的SIL验证公式[9],如式(1)~式(4)所示:
PFD1oo1=(λDD+λDU)tCE
(1)
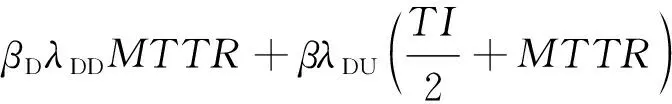
(2)
PFD2oo2=2(λDD+λDU)tCE
(3)
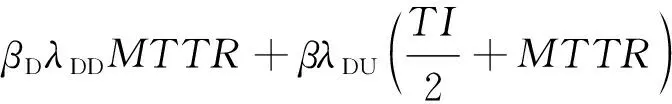
(4)
式中:λDD——检测出的危险失效率,h-1;λDU——未检测出的危险失效率,h-1;β——未检测出的共因失效分数;βD——检测出的共因失效分数;tCE——与通道相关的等效平均停止工作时间,h;tGE——与系统相关的等效平均停止工作时间,h;MTTR——平均恢复时间,h;TI——检测时间间隔,h。
其中,tCE,tGE的计算公式如式(5)~式(6)所示:
(5)
(6)
式中:DC——诊断覆盖率,%。
根据计算的PFD结果,参照SIL等级与PFD的关系表得到对应的SIL等级[10],见表1所列。

表1 SIL等级与PFD的关系
1.2 不确定性因素分析
鉴于油气站场内工艺流程失效后造成的后果较严重,通常采用高可靠、低失效的可编程电子设备,该类设备历史失效次数少,现场失效数据往往不足,因此很难捕捉到1.1节公式中的确切值。但技术人员在SIL验证的过程中,通常采用一个工况条件下精确值进行计算,由此得到的SIL等级实际上是这一特定工况下的完整性情况,该方案对技术人员的经验具有较高的依赖程度,从而夸大或缩小实际的风险水平。
针对SIL验证中的不确定性,主要分为模型不确定性、参数不确定性和人因不确定性等。模型不确定性是指评估模型在假设条件上对评估结果的影响,但随着冗余系统中逐渐将共因失效、非共因失效考虑入内,这种不确定性正逐渐改善;参数不确定性为模型中引入了不确定参数、可靠性试验条件不足、存在专家经验等造成的结果变化;人因不确定性为技术人员因个人认知、决策水平和理解能力等造成的不确定性。鉴于λDD,λDU,MTTR,TI,β等参数难以获得高质量的数据,因此本文主要考虑参数不确定性对SIL验证的影响。根据各类参数的概率分布情况,将参数不确定分为三类,见表2所列。

表2 参数不确定的分类及说明
针对表2中的分类情况,对于“信息充分”时,直接采用式(1)~式(6)计算;对于“部分信息已知”时,采用蒙特卡洛模拟的方式获得仿真数据;对于“少数信息已知”时,采用模糊理论获得分析结果。
2 实例分析
以某站场内储罐区的高完整性压力保护系统(HIPPS)为例进行分析,如图1所示。当罐顶压力传感器检测到罐内压力高时,信号传递至逻辑控制器,逻辑控制器根据检测结果对进口管线上的压力泄放阀下达关闭命令,避免储罐和下游管线发生超压,达到安全保护的目的。图1中,传感器为“2oo3”冗余结构,逻辑控制器为“1oo2”冗余结构,压力泄放阀为“1oo2”冗余结构。
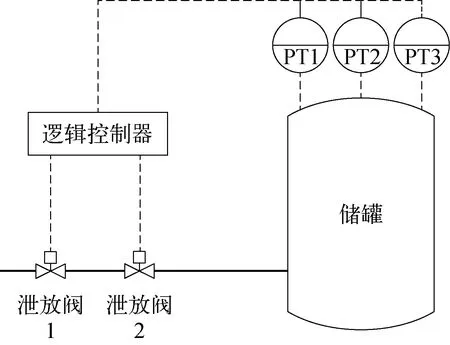
图1 高完整性保护系统(HIPPS)结构示意
2.1 基于蒙特卡洛的SIL验证方法
1)根据蒙特卡洛思想,提出基于蒙特卡洛的站场工艺安全系统冗余结构的硬件完整性评价方法。流程如下:
a)确定λDD,λDU,MTTR,TI,β等参数服从的概率密度分布类型。
b)按照确定的分布类型,采用随机数生成器,生成一组输入值,代入式(1)~式(6)验算,得到一个输出结果y(PFD)。
c)重复执行步骤a)~b),直到产生n个独立计算结果,根据大数定理可知,当n足够大时,随机变量的数学期望和算数平均值相等,此时可通过增加执行次数,增加计算结果稳定性。
d)获得输出y的最大值、最小值、均值、标准差等统计结果,为了区分PFD在不同SIL等级区间的情况,采用95%的置信区间检验当前PFD是否包含在所需的SIL等级内,计算如式(7)所示:
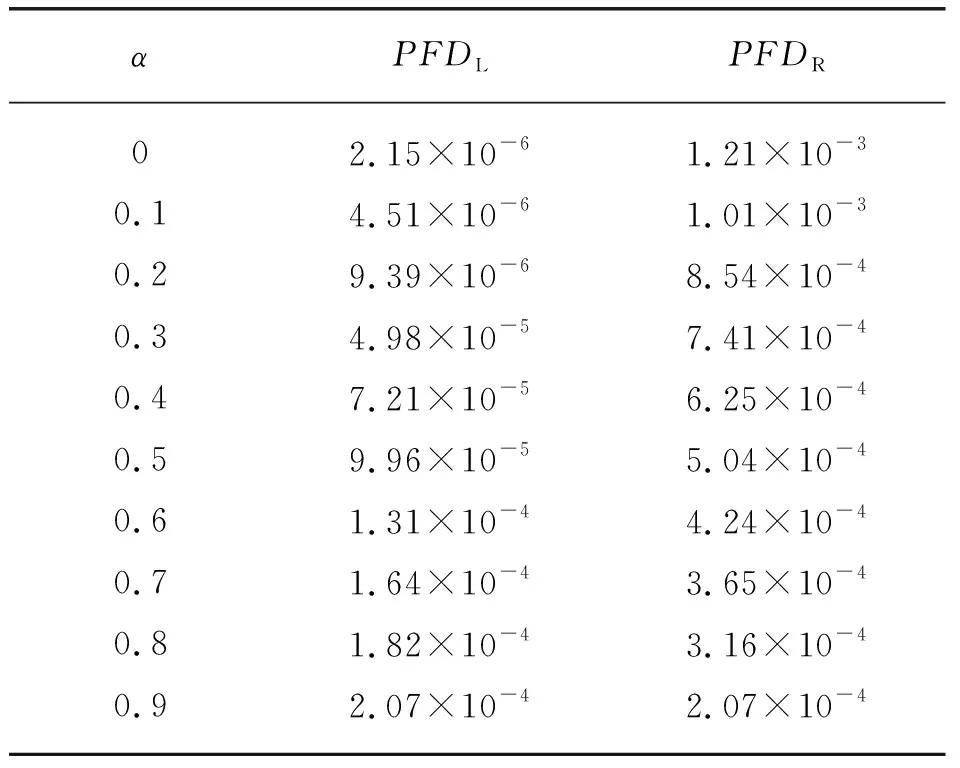
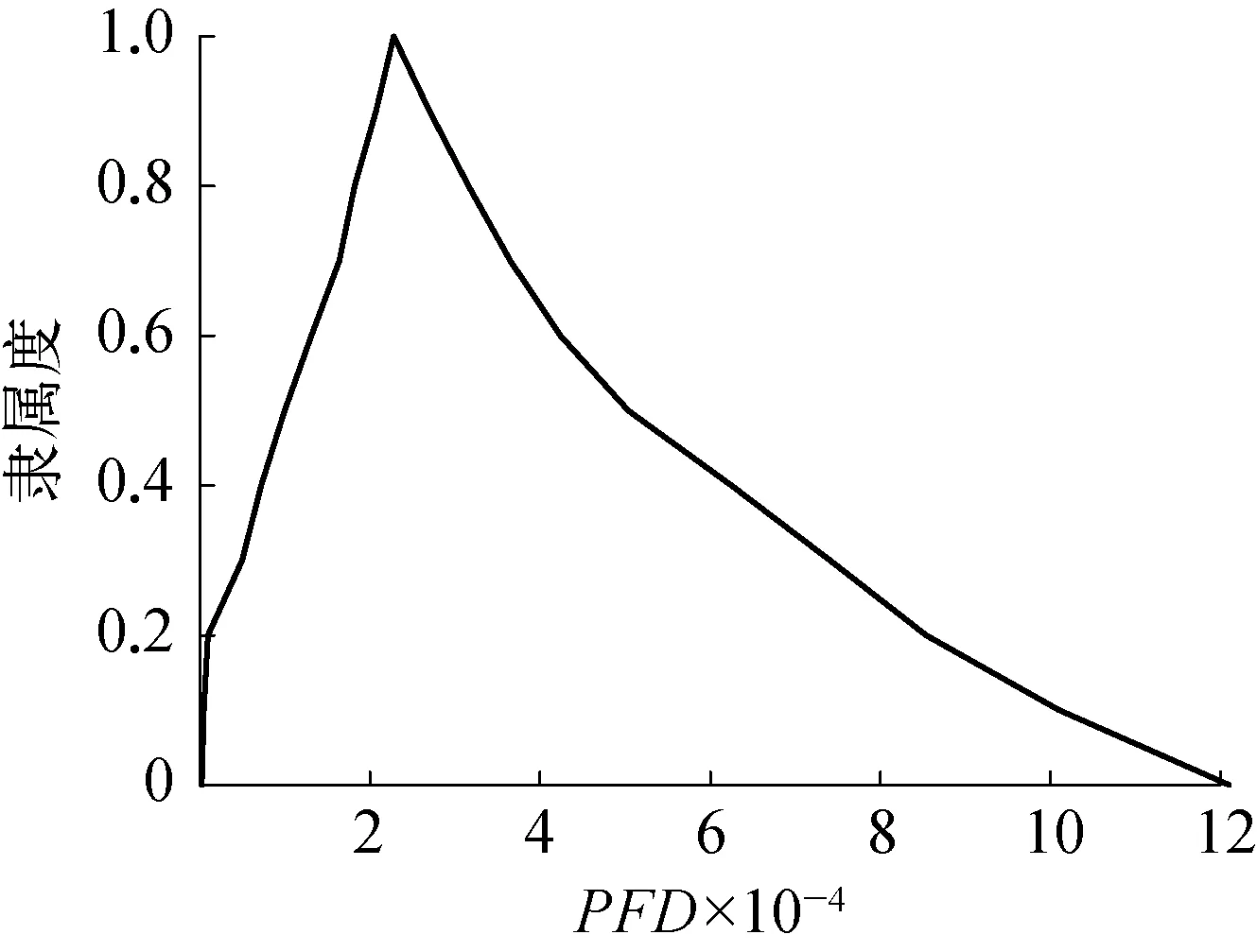
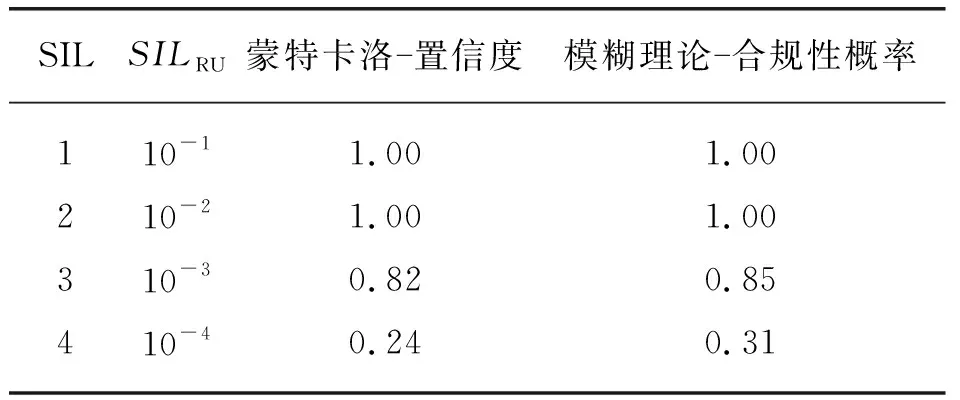
P(y (7) 式中:y——计算得到的PFD值;SILRU——所需的SIL等级,保守情况下将表1的上限定义为SILRU;P——累计概率分布函数。 2)验算。以压力泄放阀的SIL验证为例进行验算。对于危险失效率λD,IEC 61508中给出的范围为0.05×10-6~2.50×10-5,PDS手册中给出了最可能值为5.0×10-6;对于DC,IEC 61508中给出的取值为0,60%,90%,99%,但考虑到与油气站场相关的硬件均为高可靠性设备,因此DC取0.90~0.99,最可能值为0.95;对于β,IEC 61508中的参考值为2%,10%,20%,对于双机热备的情况下,最可能值为7.5%,βD取β的0.5倍即可;对于TI,与厂家手册中的检验时间有关,在此取8 760 h;对于MTTR,与技术人员的水平和个人经验等主观因素相关,考虑到泄放阀带有自动诊断功能,故MTTR取8 h。最终,除MTTR和TI外,其余参数均服从三角分布,取值情况见表3所列。 表3 参数取值情况(蒙特卡洛模拟) 按照上述模拟步骤,将表3中的数据代入式(2),输出结果见表4所列,输出样本的频率直方图和累计概率分布如图2所示。其中,PFD的均值为2.45×10-4,参照表1属于SIL3等级,但按照式(7)计算,当PFD为6.29×10-4时,有95%的PFD值小于6.29×10-4,说明此时的SIL等级为3,虽然与均值评定结果一致,但明显该结果具有不确定性。 图2 输出样本的频率直方图和累计概率分布示意 表4 蒙特卡洛模拟下的SIL验证结果 同理,根据SILRU计算不同SIL等级下的置信度,见表5所列。P(y<10-1)=P(y<10-2)=1,说明满足SIL2的可能性为100%;P(y<10-3)=0.82,说明满足SIL3的可能性为82%;P(y<10-4)=0.24,说明满足SIL4的可能性为24%。其中,该压力泄放阀最可能的SIL等级为SIL2,与之前的评定结果相差一个数量级。根据参数不确定性,可以得到不同等级范围内的置信度,由此确定不同工况、不同时刻下的SIL等级,对于SIL等级的动态定量评估具有重要意义。 表5 不同SIL等级下的置信度 1)根据模糊理论的相关原理,提出基于模糊理论的站场工艺安全系统冗余结构的硬件完整性评价方法。流程如下: b)将各参数模糊值代入式(1)~式(6),将其转化为具有模糊数形式的公式,以“1oo2”冗余结构为例: c)采用模糊运算法则计算模糊数,绘制隶属度函数图,隶属函数的表达式如式(8)所示: (8) d)计算不同水平截集α对应的左、右PFDL和PFDR,见表6所列。同时利用最大隶属度法和质心法对模糊数进行解模糊处理,并根据结果与SILRU的关系,确定SIL等级。 表6 不同水平截集下的PFDL, PFDR 2)对比。为了将模糊理论方法的模拟结果与蒙特卡洛模拟结果进行比较,采用工程计算中常用的梯形模糊数,模糊区间的上下限和中间值与表3一致,参数取值情况见表7所列,输出结果的隶属度函数值如图3所示。 图3 输出结果的隶属度函数值示意 表7 参数取值情况(梯形模糊数) 由表6可知,不同水平截集下的PFD结果有所不同,当α=0时,(PFDL,PFDR)=(2.15×10-6,1.21×10-3),与蒙特卡洛模拟得到的(最小值,最大值)=(4.32×10-5,1.25×10-3)相比,模糊数得到的结果具有更广泛的不确定性,更适合处理数据贫乏下的不确定性问题,这在极少信息的硬件完整性验证中具有重要意义。以PFDR为例,当α=0~0.1时,SIL等级为2;当α=0.1~0.9时,SIL等级为3,说明随着水平截集的选取,SIL等级有所上升。此外,采用最大隶属度法,即α=0.9时的PFD为2.07×10-4,与蒙特卡洛得到的均值2.45×10-4非常接近,此时以最大隶属度法解模糊化后的结果过于乐观,忽略了不确定性对结果的影响;而当α=0时的PFD取值范围过于保守,SIL等级从SIL2到SIL3不定,说明对结果有100%的不确定性,实际工况中出现这种情况的几率较小。因此,采用质心法进行解模糊化,得到的PFD为1.52×10-3,SIL等级的验证结果为SIL2,该结果较最大隶属度法提高了1个SIL等级,降低了参数不确定性对结果的影响,验证结果更具参考意义。 为了从置信度的角度评价结果的可信程度,引入合规性概率对模糊数隶属函数进行积分,评价结果与SILRU的概率关系,定义结果PFD(事件A)不大于SIL(事件B)的概率为PF,公式如式(9)所示: (9) 合规性概率计算结果见表8所列。蒙特卡洛模拟和模糊理论的结果中均为SIL2等级时的可能性为100%,且蒙特卡洛模拟结果在SIL3和SIL4的概率值较小,再次证明了模糊理论的不确定性较强,同时保守性更强。 表8 合规性概率计算结果 通过分析、梳理SIL验证模型不确定性的基础上,针对不同情况下,SIL等级评估方式如下: 1)对于“部分信息已知”的情况,采用蒙特卡洛模拟进行SIL验证,其结果中不同SIL等级的置信度水平有所不同,获得的SIL等级比均值评定结果低了1个等级,对于不同工况、不同时刻下SIL等级的动态定量评估具有重要意义。 2)针对“少数信息已知”的情况,采用模糊理论进行SIL验证,其结果中不同水平截集下的SIL结果有所不同,采用质心法进行解模糊化得到的SIL结果比最大隶属度法更具客观性。



2.2 基于模糊理论的SIL验证方法
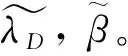



3 结 论
