水闸改进阻力系数法与有限元计算的对比分析
2023-09-12潘淑慧
潘淑慧
(菏泽市河湖流域工程管理服务中心,山东 菏泽 274000)
水闸是一种修建于河道或渠道上利用闸门控制流量和调节水位的低水头水工建筑物。在水利工程中,水闸作为挡水、泄水或取水的建筑物,应用十分广泛。平原区水闸多建于天然地基之上,由于土体本身具有一定的碎散性,因而土颗粒间便形成无数的渗流通道,在水头作用下,水流就会沿着孔隙通道渗出,目前常见的渗透破坏形式主要有管涌、流土、接触流失、接触冲刷等类型,对渗透变形的防治通常采用2个方面的措施:一方面是降低土体中的水力梯度,如地下连续墙、板桩、齿槽、帷幕灌浆等;另一方面是在建筑物下游位置设置减压井、减压沟,贯穿上部弱透水层,使局部较高的水力梯度降下来,或在渗流逸出处增设反滤层等,即通常所说的“上防下排”[1,2]。
在水闸设计中,防渗排水设计是重要的一环。根据《水闸设计规范》(SL265-2016),土基上渗透坡降的计算主要采用改进阻力系数法,但在实际操作中该方法计算步骤复杂,需经过多次修正才能得到最终结果,为简化计算,考虑引入AutoBank 有限元软件进行渗流计算,目前AutoBank 有限元软件主要是应用于土石坝渗流稳定计算中,水闸闸基渗流机理与土石坝相近,因此在理论计算中可相互借鉴。
1 改进阻力系数法
阻力系数法是1957年根据巴甫洛夫斯基分段法理论和努麦罗夫对急变渗流区计算理论提出的,是闸坝非岩石地基中恒定渗流的一种近似计算方法,可用以确定渗流区中各处的渗流要素,包括渗透压力、渗透坡降和渗透流量等,其计算精度较高,一般误差不超过5%,为工程设计计算所采用[3]。但是,这一方法尚存在着不能计算板桩尖点水头等问题,针对上述问题我国学者对阻力系数法进行了改进,增加了通过板桩尖点的等势线划分渗流区这一过程,同时在进出口局部修正方面做了更加详细的考虑,再用努麦罗夫对急变渗流区求得的解析解计算各分段的阻力系数,最终形成一种精度更高的近似计算方法——改进阻力系数法。该方法主要计算步骤如下[4-6]。
(1)地基有效深度计算。其计算公式为:
式中:L0,S0分别为地下轮廓的水平投影长度及垂直投影长度(m)。
(2)各分段阻力系数计算。根据水闸地下轮廓的3种典型流段,计算各流段的阻力系数。进出口段阻力系数计算公式为:
内部垂直段阻力系数计算公式为:
内部水平段阻力系数计算公式为:
式中:ξ0为进出口段的阻力系数;S为板桩或齿墙入土深度(m);T为地基透水层深度(m);ξy为内部垂直段的阻力系数;ξx为内部水平段的阻力系数;Lx为水平段长度(m);S1,S2分别为进、出口段板桩或齿墙入土深度(m)。
(3)各段水头损失值计算。其计算公式为:
式中:hi为各段水头损失值(m);ξi为各段阻力系数;n为总分段数;ΔH为上下游水位差(m)。
(4)进出口段水头损失修正计算。其计算公式为:
式中:h´0为进出口段修正后的水头损失值(m);h0为进出口段水头损失值(m);β为阻力修正系数,当β≥1 时,取β=1;S´为底板埋深与底面以下的板桩入土深度之和(m);T´为板桩上游侧底板下的地基透水层深度(m);其余变量含义同上。
(5)出逸比降计算。其计算公式为:
式中:J为出口段渗流坡降值;h´0为出口段水头损失值(m);S´为地下轮廓线不透水部分渗流出口段的垂直长度(m)。
2 AutoBank有限元分析
AutoBank 有限元软件是由河海大学开发的一款渗流稳定计算软件。对于闸基渗流,符合达西定律的非均匀各向异性二维渗流场,水头势函数满足以下微分方程:
式中:φ=φ(x,y)为待求水头势函数;x,y为平面坐标;kx,ky为x,y轴方向的渗透系数(m/d)。
水头势函数φ还必须满足一定的边界条件,经常出现以下3 种边界条件:①在上游边界上水头已知条件下,φ=φn;②在逸出边界水头和位置高程相等条件下,φ=z;③在某边界上渗流量q已知条件下,kx(∂φ/∂x)lx+ky(∂φ/∂y)ly= -q,其中lx,ly为边界表面向外法线在x,y方向的余弦;其余变量含义同上。
将渗流场用有限元离散,假定单元渗流场的水头势函数φ为多项式,由微分方程及边界条件确定问题的变分形式,可导出线性方程组:
式中:[H]为渗透矩阵;{φ}为渗流场水头(m);{F}为节点渗流量(m3/s)。
求解以上方程组可以得到节点水头,据此求得单元的水力坡降、流速等物理量。
3 实例应用
3.1 工程概况
某水闸地处山东省菏泽市,共设3 孔闸门,单孔净宽3.0 m,闸底板高程36.00 m,最高蓄水位38.70 m,最大水头差2.7 m,闸室结构形式为钢筋混凝土结构,闸室顺水流方向长度为10.0 m,闸室上游设有钢筋混凝土铺盖,铺盖段顺水流方向长度为10.0 m,闸室下游连接消力池,池身为钢筋混凝土结构,消力池顺水流方向长度为10.0 m,池内梅花型布置直径50 mm排水管,闸室与铺盖及消力池连接处均设有止水。闸室渗流计算简图,如图1所示。

图1 闸室渗流计算简图
3.2 改进阻力系数法计算渗透坡降
3.2.1 地基有效深度计算
根据闸室渗流计算简图,闸基地下轮廓水平投影长度L0=27.62 m,垂直投影长度S0=1.2 m,故L0/S0≥5,此时地基有效深度计算值Te=13.81 m。根据地勘报告,闸基不透水层深度为8.24 m,因此地基有效深度以实际不透水层深度计为8.24 m。
3.2.2 各分段阻力系数及水头损失计算
根据《水闸设计规范》(SL265-2016),分段阻力系数只提供了进出口段、内部垂直段及水平段3 种情况下的计算方法,对本工程而言,闸基齿墙段及消力池斜坡段多处为倾斜结构,在计算上述轮廓阻力系数时,需将倾斜段简化为相应的水平、垂直段,然后再按公式进行计算。在计算得到各分段阻力系数后,根据各分段阻力系数占总水头差比例便可得到各分段水头损失计算值,结果详见表1。
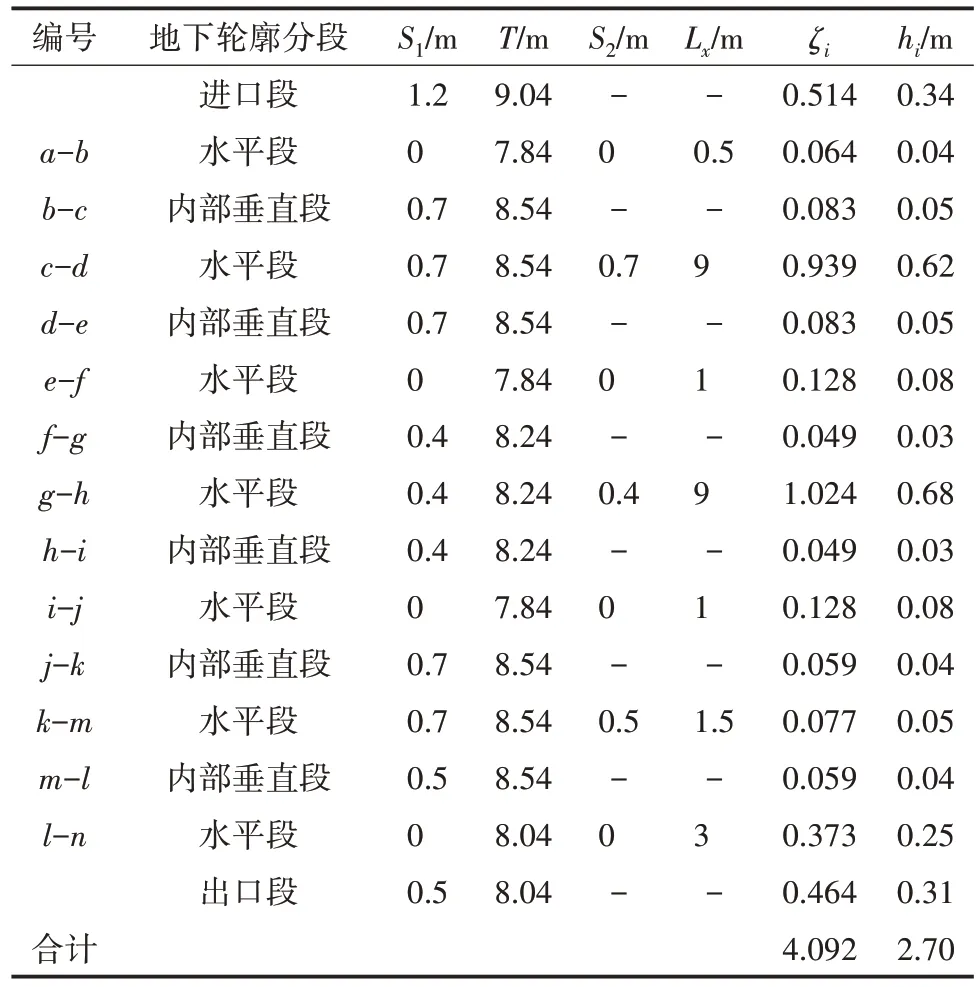
表1 某水闸分段阻力系数及水头损失计算值
3.2.3 各角点渗压水头计算
根据改进阻力系数法,闸基渗流本质上可以理解为孔隙水压力在渗流过程中的消散,即上、下游总水头差在渗径上的再分配,因此各角点渗压水头即总水头差2.7 m逐段扣减各段水头损失后的余值,据此绘制闸基渗压分布图,如图2所示。

图2 某水闸闸基渗流各角点渗压水头
3.2.4 进出口段水头损失修正计算
按照公式对进出口段水头损失进行修正,经计算,进口段阻力修正系数β进=0.80,出口段阻力修正系数β出=0.54,据此可得闸基进口段水头损失值为0.27 m,出口段水头损失值为0.17 m。
3.2.5 出逸比降计算
根据各角点渗压水头值可计算闸基渗流出逸比降值,其中闸底板水平段平均渗透坡降为Jx=0.075,渗流出口段平均逸出坡降为J0=0.34,根据地勘报告及《水闸设计规范》(SL265-2016),闸基所处地层为粉质黏土层,水平段允许渗透坡降为0.25~0.35,出口段允许渗透坡降为0.5~0.6,因此闸基渗流稳定满足规范要求。
3.3 AutoBank有限元软件计算渗透坡降
3.3.1 模型构建及材料参数
根据岩土工程勘察报告揭示的闸基地层特性,该水闸闸基不透水层深度为8.24 m,土体透水层为二元结构,土质均为粉质黏土,其中上层土垂直渗透系数kv=0.32×10-6cm/s,水平渗透系数kh=0.53×10-6cm/s;下层土垂直渗透系数kv=2.1×10-6cm/s,水平渗透系数kh=3.0×10-6cm/s。在AutoBank 软件中导入土层性质参数后建立渗流计算模型,如图3所示,模型单元数为5978个,节点数为3116个,边界数为252个。

图3 水闸闸基渗流分析有限元模型
3.3.2 渗流模拟分析
选取闸基二维稳定渗流作为计算工况,根据闸基渗流水力坡降图提取渗流逸出点处渗透坡降J0=0.365,所得计算值与改进阻力系数法计算值相近,但略高于改进阻力系数法计算结果,水闸闸基渗流水力坡降如图4所示;在整个渗流过程中,从铺盖到底板段水头消耗仅为总水头的20%左右,大部分的水头消耗于渗透水流逸出过程中,水闸闸基水头分布如图5所示,就水闸地基而言,上层土的垂直渗透系数仅为下层土的1/7 左右,因此在渗透水流穿越上层土过程中需消耗较大水头值,这也是在进行渗流分析过程中通常比较关注逸出点坡降的原因;从闸基流速分布图来看,下层土的渗流速度明显要快于上层土,这主要是由于下层土的渗透系数要远高于上层土,因而可获得更快的渗流速度,水闸闸基流速分布如图6所示。
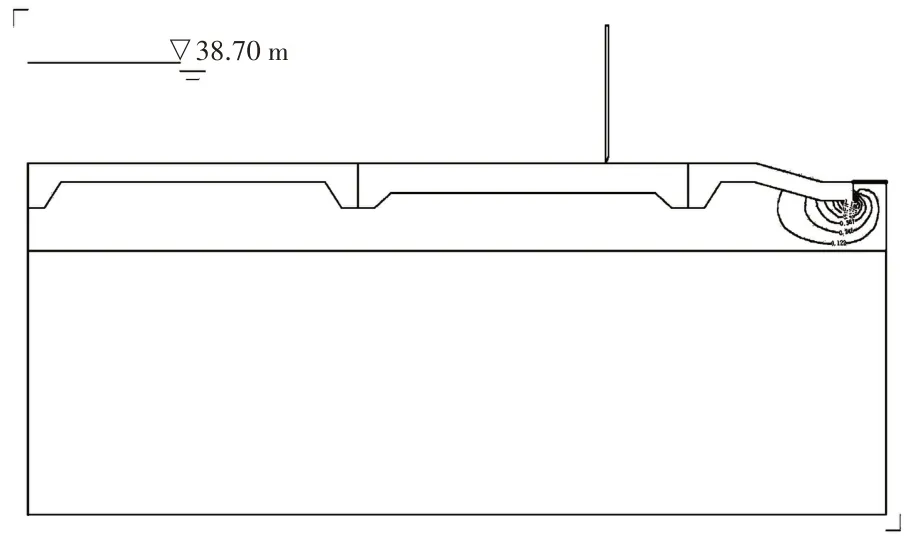
图4 水闸闸基渗流水力坡降

图5 水闸闸基水头分布
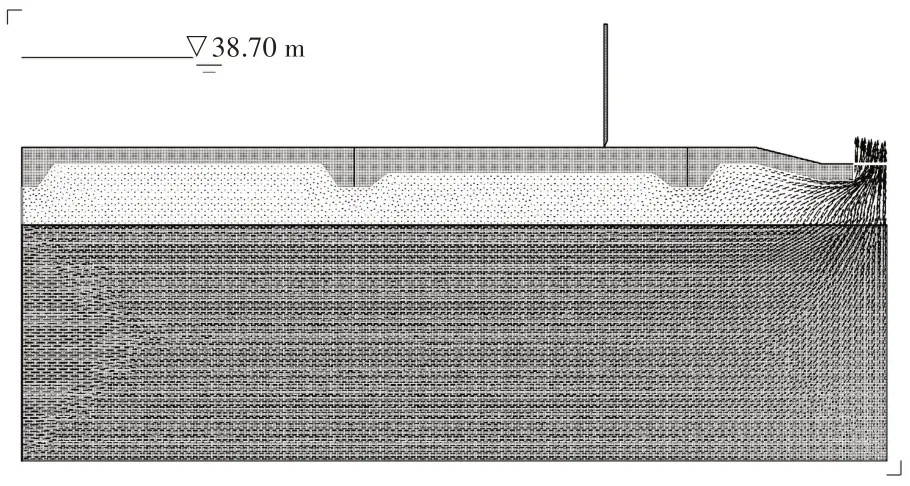
图6 水闸闸基流速分布
3.4 对比分析
通过对同一水闸工程分别采用改进阻力系数法和有限元方法计算闸基渗流,从逸出点计算坡降来看,两者是十分相近的,有限元方法计算结果略高于改进阻力系数法,从工程角度来看,这是一种偏安全的考虑;从水头分布来看,改进阻力系数法由于对渗流分区做了更加详细的划分,因而可以更加准确地求解各角点的渗压水头,而有限元方法只能导出水头总体分布情况,无法精确求解各角点的水头值;从计算的难易程度来看,改进阻力系数法计算过程复杂,且需要经过多次修正方能得到最终结果,而有限元方法可借助于AutoBank 软件进行建模,因而求解过程更加简捷。综上,AutoBank 有限元方法可用于水闸闸基渗流计算,计算结果相对可靠,但采用改进阻力系数法更为精确且该方法在工程上更加成熟,所以推荐采用AutoBank有限元方法进行渗流校核。
4 结语
为验证有限元方法在水闸渗流计算中的适用性,本文对同一水闸分别采用改进阻力系数法和有限元方法计算闸基渗流,通过对逸出点渗透坡降进行比较,改进阻力系数法计算逸出点坡降值为0.340,有限元方法计算逸出点坡降为0.365,两者计算结果相差不大,但有限元方法相比改进阻力系数法计算值偏高,在工程上偏安全,因此有限元方法可用于闸基渗流计算。同时,在计算的便捷程度上有限元方法可借鉴AutoBank 有限元软件建模,求解更加简捷。而在水头分析中,有限元方法仅能导出水头总体分布情况,结论相对粗糙,因此在实践中更加推荐改进阻力系数法,同时建议利用有限元方法进行校核计算。
