A greedy path planning algorithm based on pre-path-planning and real-time-conflict for multiple automated guided vehicles in large-scale outdoor scenarios①
2023-09-12WANGTengda王腾达WUWenjunYANGFengSUNTengGAOQiang
WANG Tengda(王腾达),WU Wenjun,YANG Feng,SUN Teng,GAO Qiang②
(∗Faculty of Information Technology,Beijing University of Technology,Beijing 100124,P.R.China)
(∗∗The 54th Research Institute of CETC,Shijiazhuang 050081,P.R.China)
Abstract With the wide application of automated guided vehicles (AGVs) in large scale outdoor scenarios with complex terrain,the collaborative work of a large number of AGVs becomes the main trend.The effective multi-agent path finding (MAPF) algorithm is urgently needed to ensure the efficiency and realizability of the whole system.The complex terrain of outdoor scenarios is fully considered by using different values of passage cost to quantify different terrain types.The objective of the MAPF problem is to minimize the cost of passage while the Manhattan distance of paths and the time of passage are also evaluated for a comprehensive comparison.The pre-path-planning and real-time-conflict based greedy (PRG) algorithm is proposed as the solution.Simulation is conducted and the proposed PRG algorithm is compared with waiting-stop A∗and conflict based search (CBS) algorithms.Results show that the PRG algorithm outperforms the waiting-stop A∗algorithm in all three performance indicators,and it is more applicable than the CBS algorithm when a large number of AGVs are working collaboratively with frequent collisions.
Key words: automated guided vehicle (AGV),multi-agent path finding (MAPF),complex terrain,greedy algorithm
0 Introduction
Automatic guided vehicle (AGV) has been widely developed and applied with the rapid development of the electronic technology and control theory.As a highly intelligent mobile robot,AGV can realize safe,reliable and efficient transportation.Hence it can replace traditional manual transportation when necessary[1].It arises in many real-world applications,such as warehouses[2],outdoor hazardous environments and office robots[3].Further,driven by the demand for flexibility and efficiency in those scenarios,it is expected that more and more mobile robots will be deployed and work collaboratively.Therefore,path planning for multi-AGV cooperation is a key technology to support the applications.
Multi-agent path finding (MAPF) is a problem that computes a set of collision-free paths for multiple agents connecting their respective starting points and destination while optimizing certain measures of paths.Finding an optimal solution for MAPF problem is NPhard because the state space grows exponentially with the number of agents[4].To implement MAPF in realworld applications,research on efficient algorithms is of great significance.At present,the algorithms of multiagent path finding problem proposed by researchers can be broadly classified into two categories: search-based algorithms and learning-based algorithms.
Generally,the search-based MAPF algorithms for AGV applications are based on heuristic search algorithms.They can be divided into two main categories:optimal path planning and approximate optimal path planning.
In optimal approaches,the standard admissible algorithm is proposed based on the A∗algorithm for single agent path planning,and the robot team is considered as a composite agent with a very high dimension,which needs to find a solution for all agents[5].However,it suffers from an exponential growth in planning complexity with the increase of the number of robots.On this basis,the technology of operator decomposition and independent detection is introduced.Their combination can optimally solve the relatively large problem in milliseconds[6].Then,the standard admissible algorithm is extended to the M∗algorithm[7]and its variants.The path is planned for each agent in advance.When the robot collides and blocks during path planning,the dimension of the search space will locally increase to ensure that an alternative path can be found.Because agents will coordinate only when it is necessary,the computing cost is greatly reduced.ODrM∗algorithm[8]further reduces the number of agents requiring joint planning by decomposing the agents into independent conflict sets,and the operator decomposition method is also used to plan the path for each agent.
Unlike the above A∗-based methods that transform the problem into a single joint agent model,the conflict based search (CBS)[9-10]and its variants are a tree search method.It plans for a single agent and constructs a set of constraints on nodes when illegal actions are detected to find the optimal solution without exploring high-dimensional space.In many cases,this reformulation enables CBS to examine fewer states than A∗-based methods while still maintaining optimality.However,CBS needs to plan a complete path for all agents in advance,which has poor real-time performance and scalability.Besides,an alternate iterative conflict-based search (AICBS) algorithm is proposed,it saves search time by checking whether there is a conflict at each step of the extension to avoid invalid plans.However,there are multiple suboptimal plans which occupy system resources[11].
In approximate optimal path planning approaches,many researchers have made improvements also based on the A∗algorithm.Cooperative A∗(CA∗) searches space-time for a non-colliding route.Hierarchical cooperative A∗(HCA∗) uses an abstract heuristic to boost performance.Windowed hierarchical cooperative A∗(WHCA∗) limits the space-time search depth to a dynamic window,spreading computation over the duration of the route[12].Flow annotation replanning(FAR)implements a flow restriction idea inspired by road networks.The movement along a given row (or column) is restricted to only one direction,avoiding head-to-head collisions.The movement direction alternates from one row (or column) to the next.After building the search graph,an A∗search is independently run for each mobile unit[13].Some also divide the map into subgraphs with known structures,and then search in a smaller subgraph configuration space[14].
In recent years,with the rapid development of deep reinforcement learning,the learning-based distributed multi-agent path planning algorithm has emerged.Agents make decisions by inputting local observations into neural networks.In pathfinding via reinforcement and imitation multi-agent learning (PRIMAL)[15]and its variants[16],deep reinforcement learning and imitation learning are combined to alleviate the problem of low sample efficiency and provide intensive rewards for agents.However,imitation learning may lead to overfitting problems.A distributed multi-agent routing method based on deep reinforcement learning is proposed in Ref.[17],which uses local and global guidance mechanisms and combines course learning to help agents plan feasible paths.
At present,there has been an in-depth study of path planning algorithms,but there is still a lack of research on the MAPF in the new large-scale outdoor hazardous application scenario,such as mining areas,coking contaminated sites and natural disaster rescue sites.Different from the dominating multi-AGV cooperation scenarios,these scenarios have complex terrain,which includes ramps or pits besides obstacles.By refinement modeling of complex terrain,the accuracy and effectiveness of the paths planned by the algorithm can be improved.There are also a large number of agents in large-scale scenarios.Most graph-based search algorithms will fail when the number of AGVs is large due to the increase in computational complexity.Therefore,an effective path planning method is still needed to ensure the efficiency of the whole system.
In this paper,the complex terrain and the cooperation among a large number of AGVs in outdoor hazardous scenarios are fully considered.The pre-path-planning and real-time-conflict based greedy (PRG) algorithm is proposed to solve the multi-agent path finding problem.The algorithm is evaluated from three aspects,which are the cost of passage,the time of passage and the distance of path.Experiments comparing the proposed PRG algorithm,waiting-stop A∗algorithm and CBS algorithm are presented.The contribution can be further summarized as following three points.
(1)The complex terrain of outdoor hazardous scenarios is fully considered.In the scenario model,different terrains are quantified into three categories,which are the impassable obstacle,the passable slopes and pits and the flat area.Different values of passage cost are defined for different terrain types.This makes the modeling more relevant to the actual scenario.
(2)The objective of MAPF is designed as minimizing the cost of passage,the time of passage and the distance of the path considering the characteristic of the complex terrain.As the outdoor area is not flat,the energy consumption and control complexity of passthrough different terrain types are different.Therefore,in addition to the time of passage and the distance of the path,the cost of passage becomes an important factor in the evaluation of the effectiveness of MAPF algorithm.This is considered in the work for a more comprehensive comparison of different algorithms.
(3) PRG algorithm is proposed to solve the complex MAPF problem for a large number of AGVs in large outdoor scenarios.As more AGVs work collaboratively in the scenario,more conflicts will occur.This dramatically increases the complexity of MAPF problem.Hence,the existing algorithms may face the problem of efficiency or effectiveness.Taking both aspects into account,the pre-path-planning information which reduces the calculation cost of implementation and the real-time collision information which improves the effectiveness are used to design PRG algorithm.
The rest of this paper is organized as follows.The model of MAPF problem in large-scale outdoor hazardous scenarios is given in Section 1.In Section 2,the PRG algorithm is proposed to generate the optimal path.Then,the simulation results and analysis are discussed in Section 3.Finally,conclusions are drawn,and future work is discussed in Section 4.
1 Scenarios and models
1.1 Map model of the working area
In this paper,the applications which require a large number of AGVs cooperatively working in outdoor hazardous scenarios are considered,and MAPF problem for those AGVs is the main concern.
Inspired by the existing MAPF model,the map of the working area is modeled by grids.As shown in Fig.1,the map withM×Mgrids is used.Different terrains in the working area are quantified into three categories,which are the impassable obstacle,the passable slopes and pits and the flat area.These terrains are respectively colored in Fig.1.As the energy consumption and control complexity of pass-through different terrain types are different,the cost of passage is defined to represent the terrain type of the grid.The cost of passage of the grid in thei-th row and thej-th column is denoted bysij,and the value ofsijis selected from{CO,CP,CF} representing the passage cost of the impassable obstacle,the passable slopes and pits and the flat area,respectively.Thus,the grid map of the working area is modeled as anM×Mmatrix.
As only the unchanged terrain is modeled,Sis also called the static map.Define the density of obstacle grids and the density of slopes and pits grids in the static map areρOandρP,respectively.

Fig.1 Map of working area
Assume that there areNAGVsU={U1,…,Un,…,UN} cooperatively working in the area,and theNpairs of start grids and goal grids (Pn,Qn)n=1,…,Nare randomly selected from the girds representing flat area.It makes sure that each goal grid is reachable from its start grid in the static map,and there is no overlap among the 2Nselected grids.As shown in Fig.1,the circles are the starting grids of AGVs and the grids of the same color are the corresponding goals.
For ease of description,the system time is discretized into time steps.At each time step,AGVs move simultaneously to neighboring grids or wait at their current grids.If a grid is occupied by an AGV,it can be considered as an impassable obstacle for other AGVs.Therefore,for the grid in thei-th row and thej-th column at time stept,aij,tis used to denote the occupancy.If the grid is occupied,aij,t=CO.Otherwise,aij,t=sij.Thus,the real-time map of the working area is denoted by
In practice,the environmental information can be continuously updated through sensors and broadcast to all the AGVs in the area.Hence,assume that each AGV can obtain both the static map and the real-time map.
1.2 Definition of MAPF problem
In this paper,the classical MAPF problem is considered.As the outdoor area is not flat,the energy consumption and control complexity of pass-through different terrain types are different.Therefore,in addition to conventional path planning metrics which are the time of passage and the distance of path,the cost of passage becomes an important factor to evaluate the selected path.Hence,the optimization objective of the MAPF problem is defined as minimizing the cost of passage,the time of passage and the distance of the path.
At time stept,the AGVUncan obtain a real-time graphGn,t=(Vn,t,En,t),in whichVn,tis the set of vertexes indicating the grids,andEn,tis the set of weighted edges indicating the comprehensive cost between any two directly connected vertexes.According to the map model,there are four types of grids inVn,t,which are free vertexes,obstacle or occupied vertexes,ramps or pits vertexes and goal vertex.Obviously,the goal vertexes for different AGVs are different.Hence,the realtime graphs obtained by different AGVs are different.Like most of the classic MAPF problems,four adjacent vertexes of each vertex are defined to have direct connections to the current vertex (except for vertexes at the edge of the area).The weights of edges are defined by different path-finding algorithms.
Based onGn,t,Unselects to move to one of the adjacent vertexes or stay at the current vertex to avoid collision.Therefore,the MAPF problem can be mathematically defined as

Further,to define the collision clearly,assume all the AGVs make routing decisions successively.A collision between AGVs is either a vertex collision or an edge collision.The vertex collision is represented by a tuple 〈Ui,Uj,v,t〉 which means AGVUidecides to move to the vertexvbut AGVUjhas already reached the vertexvat time stept.The edge collision is represented by a tuple 〈Ui,Uj,u,v,t〉 which means AGVsUiandUjtraverse the same edge(u,v) in opposite directions at time stept.A solution to MAPF problem is a set of collision-free paths,each of which for each AGV.
2 PRG algorithm for MAPF problem
Finding an optimal solution for the MAPF problem is a typical NP-hard problem,which is difficult to be solved by traditional mathematical programming algorithms.Moreover,AGVs in large outdoor complex terrain scenarios need to make decisions in real-time,which requires the path planning algorithm to be implemented efficiently.Therefore,PRG algorithm is proposed in this paper.
In MAPF problem,the state of the area is changed at every time step due to the movement of AGVs.Hence,if the path from the current vertex to the goal vertex is calculated at each decision step,only the current step is optimal,and the rest of the path will not be optimal due to the change of state at each time step.Taking both the optimality and efficiency into account and inspired by the Bellman equation in reinforce learning,PRG algorithm combines the real-time-conflict-based accurate passage cost of the current step and the static-map-based estimation of the passage cost of the rest of the path to form the decision metric.Then,the current action is selected based on this decision metric using the greedy algorithm.
In the following,the three stages of PRG algorithm are described in detail.The first stage is estimating the static passage cost from each vertex to the goal vertex.The second stage is calculating the accurate passage cost of the current step using the real-time dynamic map.The third stage is conducting the decision metric and making the greedy-based decision.
2.1 Preprocess to estimate the static passage cost
As the static mapSremains unchanged in the process of path planning,the static passage cost is preestimated based onSusing Dijkstra algorithm.For AGVUn,its goal vertex isQn.The static passage cost from all the vertexes inStoQnis recorded in a static matrix denoted by
wherebij,nis the static passage cost from the vertex in thei-th row and thej-th column to the goal vertexQn.If the vertex in thei-th row and thej-th column is an obstacle,bij,nis designed to be a very large value.
IfUnis located ini-th row and thej-th column at time stept,the estimated static passage cost is calculated as
2.2 Calculate the accurate passage cost of the current step
As all AGVs make routing decisions successively,the order is defined as {U1,…,Un,…,UN}.Since the decision of each AGV will change the state of the map,further define
as the real-time map observed byUnat time stept.
IfUnis located ini-th row and thej-th column at time stept,the accurate passage cost of the current step is calculated as
where,dn,t=∅meansUnstay at the current location,andCWis the corresponding cost.
2.3 Greedy-based decision
Combining the two kinds of cost together,the decision metric forUnlocated ini-th row and thej-th column at time steptcan be calculated as
wherewSandwRare the constant coefficients.
Based on the decision metric,the action forUnat time steptis selected by
2.4 Algorithm procedure
Based on the above analysis,the specific algorithm procedure is given in Algorithm 1.

Algorithm 1 The procedure of PRG algorithm Input: the grid map with impassable obstacle,the passable slopes and pits and the flat area,and assign start and goal vertices to agents.1 Initializes the static map S and the real-time map A0,1.2 for n∈ [1,N],do 3 Calculate static passage cost matrix Bn using Dijkstra algorithm 4 end for 5 for t∈ [0,T],do 6 for n∈ [1,N],do 7 if Un reaches the goal vertex Qn,then 8 dn,t =∅.9 else 10 Observe At,n.11 Calculate {Cn,t(dn,t)}dn,t∈{U,D,L,R,∅} for all the possible actions using Eqs(7) and (8).12 Select the action d∗n,t using Eq.(9).

13 Execute the action and update the real-time map At,n+1.14 Calculate and record all the performance indicators of Un at time step t.15 e nd i f 16 end for 17 At+1,1 =At,n+1.18 if all agents reach their goal vertexes 19 break 20 end if 21 end for
3 Results and analysis
To evaluate the performance of PRG algorithm,a simulation environment is conducted,and the waitingstop A∗algorithm[18]and CBS algorithm[9]are also implemented for comparison.Three performance indicators which are the time of passage,the distance of path and the cost of passage are compared.The detailed simulation setting and the results are given in the following.
3.1 Simulation setting
The simulation environment is Python 3.8.The configuration parameter of the PC is as follows.The processor is Intel(R) Core (TM) i5-9300H CPU @2.40 GHz 2.40 GHz.The memory is RAM 8.00 GB.The system type is a 64 bit operating system based on the X64 processor,and the operating system version is Windows 10.Simulation parameters are shown in Table 1.

Parameter Value Map sizes M {50,80}Density of obstacles ρO{0.05,0.10,0.15,0.20,0.25}Density of slopes and pits ρP 0.1 Number of AGVs N 16,32,…,144{}{ }Coefficients in decision metric wS,wR Cost of passage {CO,CP,CF,CW} 160,3,1,3{ } {1,1}
A sample in the performance evaluation is considered as a map with randomly generated obstacles,ramps,pits and AGVs.The simulation parameters are given in Table 1.For each group of simulation parameters,50 samples are generated and simulated to obtain convincing results.
3.2 Comparison algorithms
The proposed PRG algorithm is compared with the waiting-stop A∗algorithm[18]and CBS algorithm[9]to reveal its advantages.The waiting-stop A∗algorithm uses the A∗algorithm to plan the shortest path for all AGVs in advance.When two AGVs are about to collide,the conflict is resolved by waiting or giving way.Specifically,when a vertex conflict occurs,that is,the next position of the current AGV has been occupied,AGV will choose to wait and then enter the next position.When an edge conflict occurs,that is,two AGVs are moving towards each other,then an AGV will randomly select an accessible adjacent vertex and give way to another AGV.CBS algorithm[9]consists of two layers of the search process,and the low-level searches an effective path for each AGV.The high-level search is responsible for checking path collisions and selecting the least costly branch to re-search the low-level path until the high-level search finds a valid path.
To facilitate the interpretation of simulation results,the complexity of the three algorithms is also analyzed in advance.The complexity indicator used here is the total number of floating-point operations (FLOPs)required to carry it out.As for the waiting-stop A∗algorithm,its computational complexity is mainly determined by the A∗algorithm.The time cost for the A∗algorithm isΟ(p3) ,wherep=M2is the number of vertexes in the map.Since it is necessary to plan a path for each AGV in advance,and the number of AGVs andpare of the same order of magnitude,the computational complexity of the waiting-stop A∗algorithm isΟ p4( ).The computational complexity of the proposed PRG algorithm is similar to the waiting-stop A∗algorithm.It is mainly determined by the Dijkstra algorithm,which is a variation of the A∗algorithm.Hence,the computational complexity is alsoΟ p4( ).However,in CBS algorithm,the computational complexity of the high-level search process isΟ2q( ),whereqis the number of collisions encountered during the solving process of high-level search tree of CBS.The low-level search algorithm is A∗algorithm,so the computational complexity of CBS isΟ( 2qp4),which means it is more difficult for CBS to compute results in real time especially when the number of AGVs is large.
3.3 Simulation results
First,the performance of the three algorithms is tested when the number of AGVs is fixed asN=25 in the map of size 50 ×50.To test the adaptability of the algorithms to changes in the static environment,the density of obstacles varies asρO={0.05,0.1,0.15,0.2,0.25},which accordingly means the numbers of obstacles grids in the map are {125,250,375,500,625}.Under these situations,the paths between two connected vertexes in the static map are different.Besides,the probability of dynamic collisions increases with the increase in the density of obstacles due to the reduction in the passable vertexes although the number of AGVs is fixed.Results are shown in Figs 2,3 and 4.

Fig.2 Average distance of paths with various ρO
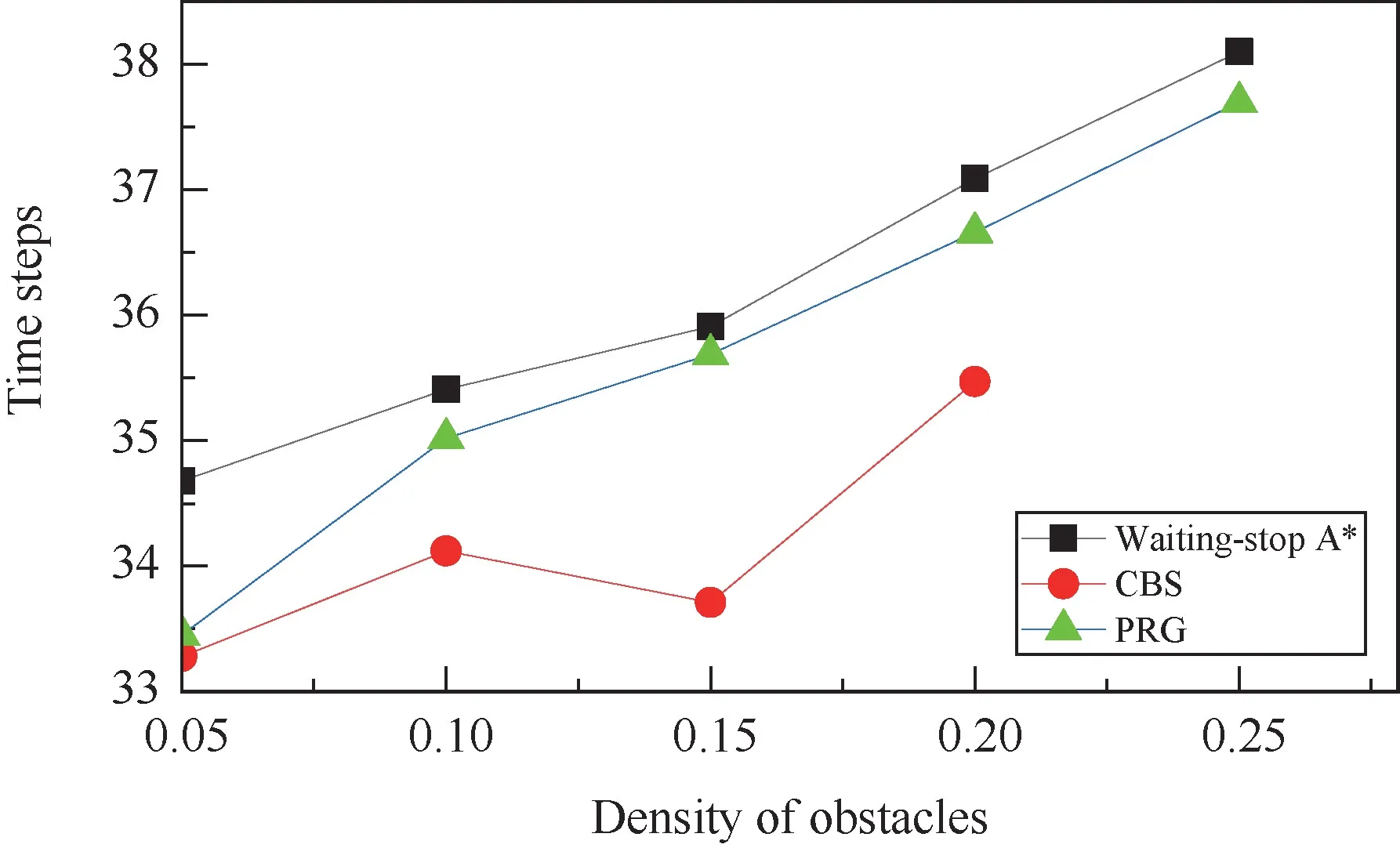
Fig.3 Average time of passage with various ρO
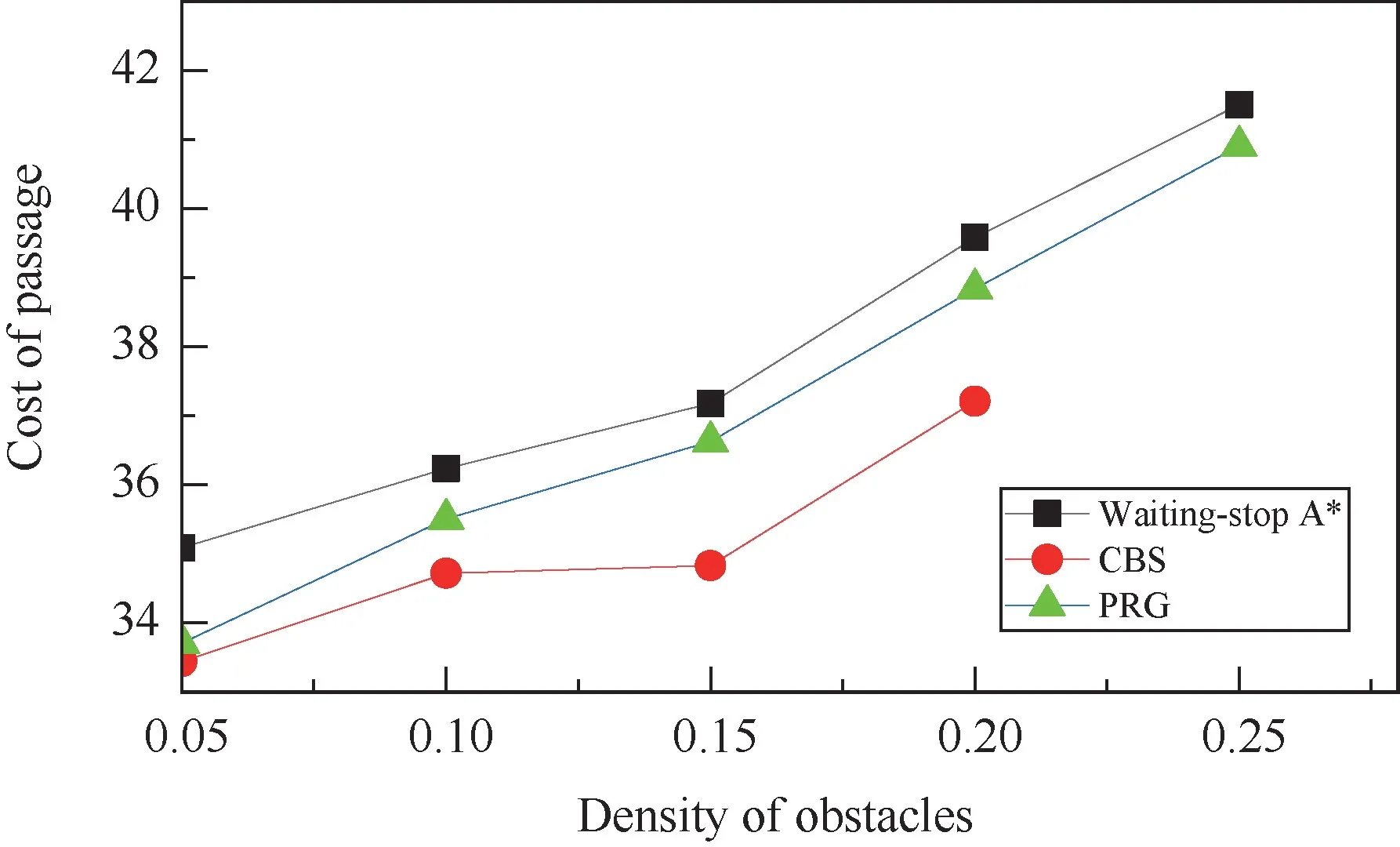
Fig.4 Average cost of passage with various ρO
Obviously,as an optimal centralized path planning algorithm,CBS algorithm performs the best in all the three performance indicators evaluated here.However,with the increased density of obstacles,the number of collisions encountered increased.When the density of obstacles reaches 0.25,CBS algorithm is no longer applicable in the simulation environment due to the extremely high computational complexity caused by the frequently triggered high-level search processes.
In contrast,PRG algorithm and the waiting-stop A∗algorithm are less complex and easier to implement even when there are a large number of collisions.The two algorithms obtain a similar performance of the average distance of paths measured in Manhattan distance as both are based on the pre-searched path.However,they handle dynamic collisions differently.Results show that PRG algorithms can solve collisions more effectively and perform better in terms of the average time of passage and the average cost of passage.The performance gain obtained by PRG algorithm is between 1.0%and 4.0% when the value ofρOvaries.
To further evaluate the ability of PRG algorithm in handling dynamic collisions,the simulations with different numbers of AGVs in a map are conducted.The map size is 50 ×50 andρO=0.05.The number of AGVs varies asN= {16,32,48,64,80,96,112}.Results are shown in Figs 5,6 and 7.

Fig.5 Average distance of paths with different number of AGVs (M=50)

Fig.7 Average cost of passage with different number of AGVs (M=50)
Similar to the previous group of simulations,CBS algorithm performs the best in all the three performance indicators evaluated here.Unfortunately,when the number of AGVs is larger than 48,CBS algorithm is no longer applicable in the simulation environment due to the extremely high computational complexity.Existing research also confirmed that using CBS algorithm to compute an optimal solution when the number of AGVs is larger than 50 is often intractable[19].This means CBS algorithm is not suitable for the scenario in which a large number of AGVs are working collaboratively.
Compared with the waiting-stop A∗algorithm,PRG algorithm performs better in terms of the average distance of paths,the average time of passage and the average cost of passage,and the performance gains peaked at 2.4%,8.5% and 7.5%,respectively.When collisions occur,PRG algorithm can make decisions based on the real-time map of the working area,which can reach the goal vertex more flexibly.Meanwhile,the waiting-stop A∗algorithm resolves collisions only by two pre-defined rules which are waiting or giving way.Therefore,with the increase in the number of AGVs,collisions occur more frequently,and the performance gain of PRG algorithm is more obvious.This means PRG algorithm can well adapt to dynamic environments with frequent collisions and maintain a low implementation complexity.
The performance of PRG algorithm in the large working area is also evaluated.The map size is set as 80 ×80 withρO=0.05.The number of AGVs varies asN= {16,32,48,64,80,96,112,128,144}.Results given in Figs 8,9 and 10 show the same trends as that shown in Figs 5,6 and 7.Thus,the effectiveness and efficiency of PRG algorithm are confirmed again.
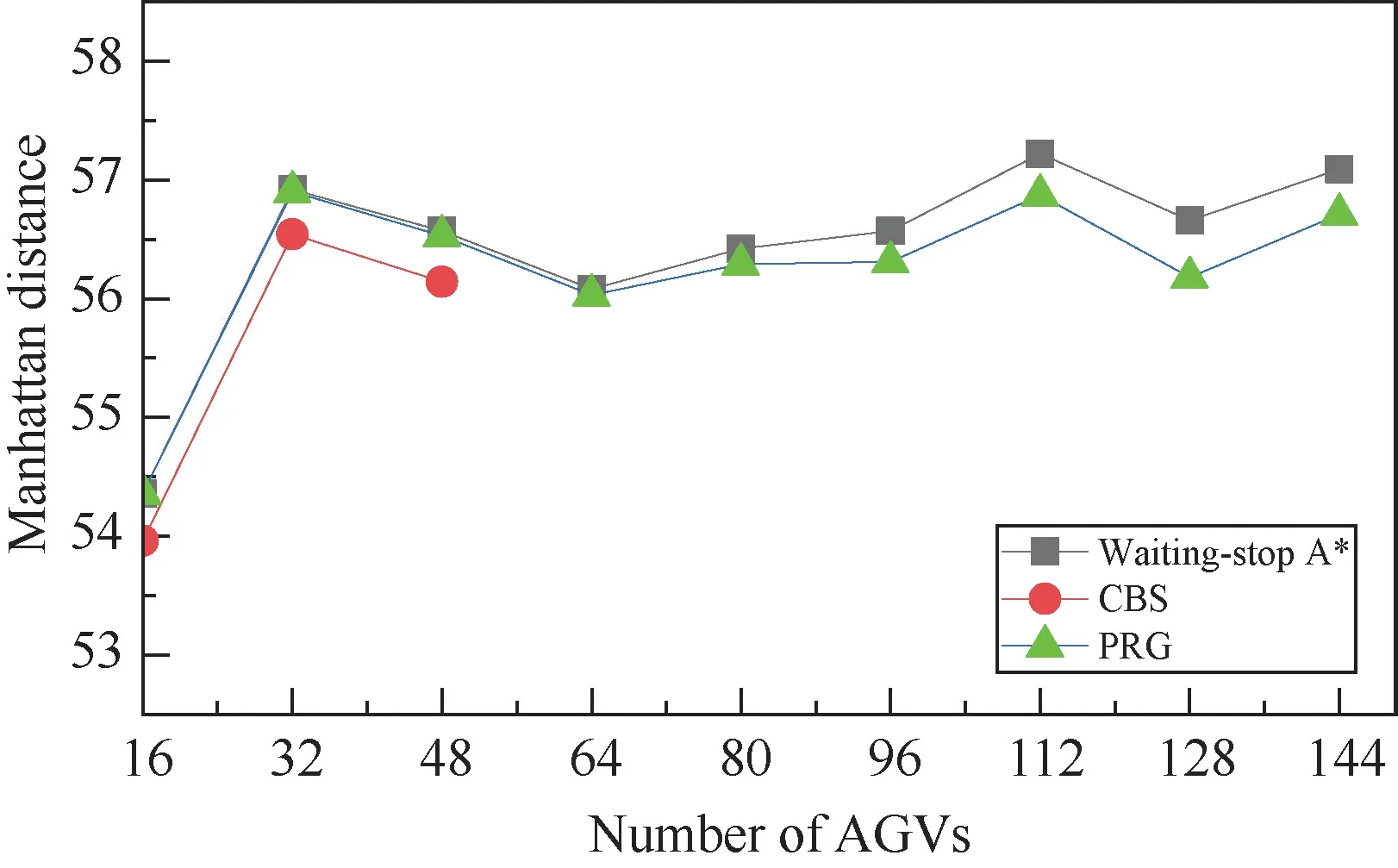
Fig.8 Average distance of paths with different number of AGVs (M=80)

Fig.9 Average time of passage with different number of AGVs (M=80)
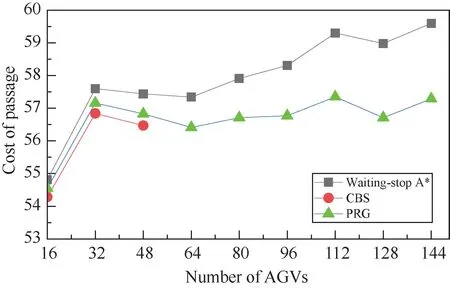
Fig.10 Average cost of passage with different number of AGVs (M=80)
4 Conclusions
This paper considers the MAPF problem for a large number of AGVs in outdoor hazardous scenarios with complex terrains and proposes the PRG algorithm combining the real-time-conflict-based accurate passage cost of the current step and the static-map-based estimation of the passage cost of the rest of the path to form the decision metric.The objective of MAPF problem is to minimize the cost of passage while the Manhattan distance of paths and the time of passage are also evaluated for comprehensive comparison.Simulation results show that PRG algorithm performs better than the waiting-stop A∗algorithm in all three performance indicators evaluated in this paper.Compared with CBS algorithm,the performance of PRG algorithm is similar when the number of AGVs is small.When the number of AGVs is moderate,CBS algorithm performs the best.However,CBS algorithm is not applicable to the scenario in which a large number of AGVs are working collaboratively with frequent collisions.In all,PRG algorithm is a practical solution for MAPF problem in largescale scenarios with a large number of AGVs.It obtains a good trade-off between complexity and performance.Its effectiveness and efficiency are confirmed through simulation.
In the future,multi-agent cooperative path planning methods based on deep reinforcement learning should be explored to further improve performance.
猜你喜欢
杂志排行
High Technology Letters的其它文章
- End-to-end aspect category sentiment analysis based on type graph convolutional networks①
- A wireless geophone based on STM32①
- Research on system combination of machine translation based on Transformer①
- The relationship between extra connectivity and t/k-diagnosability under the PMC model①
- Deep reinforcement learning based task offloading in blockchain enabled smart city①
- Design of two-dimensional spatially coupled LDPC codes for combating burst erasures①
