黄河流域多源蒸散发产品评估
2023-09-12韩再惠吴志俊达古拉李琼芳
韩再惠,陈 燕,吴志俊,任 黎,苗 平,达古拉,李琼芳,5
(1.内蒙古自治区鄂尔多斯市杭锦旗水利事业发展中心,内蒙古 鄂尔多斯 017400;2.河海大学水文水资源学院,江苏 南京 210024;3.内蒙古自治区鄂尔多斯市河湖保护中心,内蒙古 鄂尔多斯 017400;4.内蒙古自治区鄂尔多斯市水利事业发展中心,内蒙古 鄂尔多斯 017400;5.江苏省南京市长江保护与绿色发展研究院,江苏 南京 210024;)
1 概述
地表蒸散发是土壤-植被-大气系统中能量与水分转换的主要过程,也是能量平衡与水量平衡的关键组成因素。因此,准确估算地表蒸散发对区域水循环和水资源综合利用方面具有重要意义[1]。然而由于空间异质性和观测站点稀疏等原因,传统基于站点数据估算蒸散发的方法存在较多问题。因此,国内外研究者们开发了不同类型的大尺度地表蒸散发估算方法,总共可分为5类:经验统计公式、遥感正蒸散模型、陆面水文模型、基于蒸散发互补方法地表蒸散发模型和基于水量平衡的蒸散发估算方法,并依托这些方法陆续生产和发布了不少全球和区域尺度的蒸散发数据产品[2]。然而,Zhang等[3]发现大多数蒸散发产品在计算冠层气孔阻力时,未能将蒸散发和植被初级总生产力(Gross Primary Productivity,GPP)耦合起来。因此,不能充分考虑不同环境因子对植被冠层气孔导度的影响,在流域尺度上的地表蒸散发估算存在较大的不确定性。但遗憾的是,目前为止很少有研究在计算蒸散发的过程中引入GPP过程。
与此同时各类蒸散发产品由于模型结构、输入数据集、模型参数存在差异等原因,都不可避免地有一定的不确定性。因此,迫切需要对其在蒸散发估算中的精度和不确定性进行分析。水量平衡法能够在流域尺度对蒸散发估算值进行较为精准的验证,因此被业内研究者广泛使用[4]。TCH方法则可以在没有蒸散发观测值的情况下,量化流域蒸散发栅格尺度上的不确定性[5]。目前,在区域尺度上对蒸散发产品评价的研究较多,但均未对引入GPP过程的遥感蒸散发模型和传统蒸散发产品在不同时空尺度上采用不同方法进行综合对比研究。本研究通过引入GPP过程以实现对遥感蒸散发模型的改进,并采用水量平衡方法和TCH方法,综合对比评价改进SW模型和不同蒸散发产品在黄河流域不同时空尺度下的精度和不确定性,以期为更加准确估算黄河流域蒸散发提供有益参考。
2 数据来源与研究方法
2.1 研究区概况
黄河流域位于中国的北部地区,面积为7.95×105km2(如图1所示)。多年平均气温为7.2℃,多年平均降水量为495.6mm。由于地理位置,地形,植被覆盖等因素影响,该流域全年降水分布极不均匀,约60%~80%的降雨量集中在6—9月。流域主要植被类型为常绿针叶林(ENF)、落叶针叶林(DNF)、常绿阔叶林(EBF)、落叶阔叶林(DBF)、灌丛、草地和农田[6]。本研究根据黄河流域自然地理环境特征,选择花园口水文站作为黄河流域的径流控制站。该水文站的控制流域面积为7.3×105km2,约占黄河流域面积的92%。
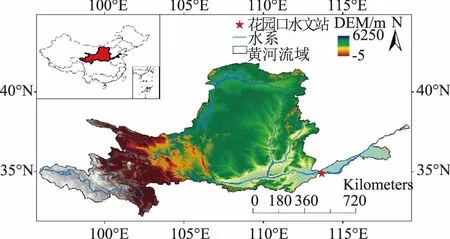
图1 研究区地理空间分布
2.2 数据收集与处理
本研究采用了两种被广泛使用的蒸散发产品,改进SW模型所需的气象和遥感数据,GRACE及GRACE-FO重力探测卫星的陆地水储量数据以及实测径流数据。各数据集具体信息详见表1。依据表1,选定2003—2017年作为研究时段,并采用双线性插值法将各数据集的空间分辨率统一重采样至0.1°×0.1°。

表1 蒸散发产品特征信息
2.3 SW双源蒸散发模型的改进及应用
SW模型是由Penman Monteith模型发展而来的双源蒸散发模型。SW模型的详细信息可以参考Shuttleworth[11]和Hu[12]等人的研究,模型可用以下公式表示:
λET=CsPMs+CcPMc
(1)
PMs=ΔR+[ρcpVPD-ΔracRs]/
(2)
PMc=ΔR+[ρcpVPD-ΔracRs]/
(3)
式中,PMs、PMc—土壤蒸发、冠层蒸腾,mm;Cs、Cc—土壤表面阻力系数、冠层阻力系数;ρ—气体密度,kg/m3;—饱和蒸气压-温度曲线的斜率,kPa/k;γ—恒定常数,kPa/k;VPD—蒸气压差,kPa;R、Rs—冠层上方、土壤表面的净辐射通量;rac—叶片至冠层高度的空气动力阻力,s/m;ras—土壤表面至冠层高度的阻力,s/m;raa—冠层
高度至参考高度的阻力,s/m;rss—土壤表面阻力,s/m;rsc—冠层气孔阻力,s/m。
本研究采用Hu等人[12]的研究在SW模型基础上引入Ball-Berry气孔导度模型,以解决在区域尺度上SW模型气孔导度参数难以获取的关键问题。其中,改进SW模型的rsc计算公式如下:
(4)
式中,g0、a1—经验参数,可以参考Hu等人的研究;hs—叶片表面空气相对湿度,%,采用空气相对湿度代替;cs—CO2含量,ppm;Pn—光合速率,μmolm2s-1,是估算rsc中的关键因素,采用GLASS GPP产品替代。在本研究中,改进SW模型计算得到的黄河流域月尺度蒸散发简称为ETSW_GLASS。
2.4 基于水量平衡法的多源蒸散发产品精度验证
在缺少实测蒸散发观测数据的流域尺度下,基于降水、径流和总蓄水量变化的水量平衡方法通常被广泛用于蒸散发产品检验[13]。因此,本研究将采用流域水量平衡方法计算的黄河流域逐月蒸散发量作为“真实值”用于验证ETGLASS、ETCR、ETSW_GLASS在黄河流域的数据准确性。水量平衡方法计算蒸散发公式如下:
ETWB(i)=P(i)-R(i)-TWSC(i)
(5)
TWSC(i)=TWSA(i+1)-TWSA(i-1)/2Δi
(6)
式中,i—时间尺度,月;ETWB—水量平衡方法计算的蒸散发量,mm/月;P、R—降水量、径流量,mm/月;TWSA—总蓄水量异常;TWSC—总蓄水量变化。
2.5 基于TCH法的多源蒸散发产品不确定性评估
与传统的误差估计方法相比,TCH方法可以在未知区域蒸散真实值的情况下评估3种或更多不同数据集的不确定性[14]。本研究选取改进SW模型得到的蒸散发估算值(ETSW_GLASS)和两个被广泛使用的蒸散发产品(ETGLASS、ETCR),采用TCH方法对其在流域尺度上的不确定性进行评价。评估过程的具体细节描述如下:
Xi=Xt+εi,∀i=1,2,3,…,N
(7)
Yi,M=Xi-XR=εi-εR,∀i=1,2,…,N-1
(8)
S=cov(Y)
(9)
S=J·R·JT
(10)
(11)
式中,Xt—蒸散发产品的“真实值”;Xi—蒸散发产品的模拟值;εi—相应的随机误差值;Y—M×(N-1)的方差矩阵;M—时间样本数量;N—不同蒸散发产品数量;S—Y的协方差矩阵;R—N×N的噪声协方差矩阵;J—单位矩阵。
然而,由于未知数(N×(N+1)/2)大于方程数(N×(N-1)/2),式(10)无法求解。根据Galindo和Palacio等人研究,可以基于Kuhn-Tucker定理来解决这个问题。根据Kuhn-Tucker定理,目标函数可表示为:
(12)
其约束函数为:
H(r1N,…,rNN)=-|R|/|S|·K<0
(13)
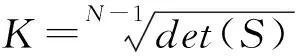
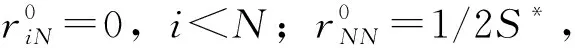
(14)
结合式(11)计算得到蒸散发产品模拟结果的方差,最后取标准差作为不确定性的结果。
2.6 多源蒸散发产品精度评价指标
本研究采用统计参数包括决定系数(R2)、均方根误差(RMSE)、平均绝对误差(MAE)作为蒸散发产品精度检验的依据。各项指标的计算公式如下:

(15)
(16)
(17)

3 结果
3.1 蒸散发产品时空格局对比分析
图2—3分别展示了2003—2017年的多年平均ETGLASS、ETCR和ETSW_GLASS在黄河流域的空间分布格局和年际变化趋势。

图2 2003—2017年多年平均蒸散发空间分布
由图2可以看出,2003—2017年黄河流域基于像元尺度的多年平均ETGLASS、ETCR和ETSW_GLASS总体上都呈现出从东南向西北逐渐减小的趋势,但不同蒸散发产品在一定程度上也表现出了较为不同的空间分布特征:ETGLASS在中部、南部和东部地区的多年平均蒸散发要明显高于北部和西部地区;ETCR的多年平均蒸散发则表现为在西南地区较高,而在北部地区较低;ETSW_GLASS的多年平均蒸散发表现出在东南部较高,西北部较低。由图3可见,2003—2017年ETGLASS在黄河流域的平均年蒸散发高于ETCR和ETSW_GLASS的平均年蒸散发值。ETGLASS和ETSW_GLASS平均年蒸散发都呈现出不显著的增加趋势,线性拟合斜率分别为2.79、2.08mm/年。ETCR平均年蒸散发呈下降趋势,斜率为-1.62mm/年。ETGLASS、ETCR和ETSW_GLASS的多年平均蒸散发分别为502.28、408.46、442.82、414.4mm。

图3 2003—2017年平均年蒸散发变化
综合表明,ETGLASS、ETCR和ETSW_GLASS估算的蒸散发在黄河流域存在时空特征差异,且ETGLASS相较于ETCR和ETSW_GLASS的差异最大,差异主要表现在:ETGLASS的逐年蒸散发与多年平均蒸散发要显著高于ETCR和ETSW_GLASS,且ETGLASS的多年平均蒸散发在北部和东部大片地区存在高估。
3.2 蒸散发产品精度评估
图4展示了2003—2017年黄河流域ETGLASS、ETCR和ETSW_GLASS月平均蒸散发和基于水量平衡方法计算的流域月平均蒸散发“真实值”(ETWB)之间的比较结果。图5展示了ETGLASS、ETCR和ETSW_GLASS月平均蒸散发与ETWB月平均蒸散发之间的决定系数、均方根误差、平均绝对误差。

图4 水量平衡蒸散发与蒸散发产品的比较

图5 水量平衡蒸散发与蒸散发产品的精度验证
从图5可以看出,尽管ETGLASS、ETCR和ETSW_GLASS的月平均蒸散发与基于水量平衡方法计算的流域月平均蒸散发“真实值”(ETWB)的对比存在高估和低估的情况,但总体上它们的月均蒸散发与月平均ETWB表现出相似的变化规律。图6中R2、RMSE和MAE的值也验证了这一点。T检验证明,在0.01的显著水平上(p<0.01),月平均蒸散发ETGLASS、ETCR和ETSW_GLASS与月平均ETWB之间存在显著相关性,且R2、RMSE和MAE值较高,表明ETGLASS、ETCR和ETSW_GLASS在黄河流域的月平均蒸散发与月ETWB具有相似的精度。由图6可知,ETSW_GLASS表现较好,具有相对较高的R2值以及较低的RMSE和MAE值。综合来看,ETSW_GLASS表现最好,其次是ETCR和ETGLASS。以上结果表明通过引入GPP过程来改进的SW模型可以提高估算黄河流域蒸散发的精度。

图6 黄河流域蒸散发产品不确定性空间分布
3.3 蒸散发产品不确定性评估
图6显示了2003—2017年黄河流域ETGLASS、ETCR和ETSW_GLASS的逐像元的月平均不确定性空间分布特性。
如图6所示,基于TCH方法确定的ETGLASS、ETCR和ETSW_GLASS在黄河流域的不确定性范围为0.04mm/月-32.53mm/月,其中不确定性最低的是ETSW_GLASS(4.66mm/月),不确定性范围为0.2~11.58mm/月,ETGLASS的不确定性最高为(11.61mm/月),不确定性范围为1.42~32.53mm/月,其次为ETCR(9.96mm/月),不确定性范围为4.42~27.55mm/月。图6也表明,ETGLASS、ETCR和ETSW_GLASS的栅格尺度月平均不确定性具有相似的空间变化特性,总体上都呈现出黄河流域西部的不确定性普遍低于东部的特征。然而,ETGLASS、ETCR和ETSW_GLASS在月均不确定性的空间分布上也都表现出一定程度的不同:ETGLASS在中部地区具有较高的不确定性,而在东部和南部地区具有较低的不确定性;ETCR在中部和西部地区的不确定性较低,东南部地区的不确定性较高;ETSW_GLASS东南部地区的不确定性较高,北部和西部地区的不确定性较低。总的来说,2003—2017年黄河流域ETGLASS和ETCR的月均不确定性高于ETSW_GLASS。以上分析也证明,通过引入GPP过程改进SW模型可以降低蒸散发估算值的不确定性。
4 结论
本文综合对比评价了ETGLASS、ETCR和ETSW_GLASS在不同时空尺度下蒸散发估算值在黄河流域的精度和不确定性,并对比分析了2003—2017年3种ET产品的时空分布格局。研究发现:
(1)ETGLASS、ETCR和ETSW_GLASS的蒸散发估算值存在差异,这些差异反映在栅格尺度年平均ETGLASS、ETCR和ETSW_GLASS的时空格局分布以及变化趋势上。
(2)就R2、RMSE、MAE而言,月ETGLASS、ETCR和ETSW_GLASS的精度与基于水量平衡方法计算的ETWB相似,其中ETSW_GLASS的表现优于ETGLASS和ETCR。
(3)ETGLASS、ETCR和ETSW_GLASS栅格尺度月均不确定性呈现出不同的空间变化特征,其中ETSW_GLASS的月均不确定性低于ETGLASS和ETCR。
后续可以在3种蒸散发产品对比评估的基础上,对不同蒸散发产品的不确定做进一步的归因分析以提高模拟精度。
