不确定条件下风力发电系统的无功优化调度

2023-09-12王聪

仪器仪表用户 2023年10期

王聪

（国网山东省电力公司郓城县供电公司，山东郓城 274700）

0 引言

竞争激烈的商业环境迫使电力系统在其安全边际附近运行。因此，电压不稳定和崩溃更有可能发生。然而，无功资源的优化规划，可以提高电压稳定裕度。这是一个多目标优化问题，称为最优无功功率调度（ORPD）。系统安全性和经济性是这个优化问题的共同目标[1,2]，发电机和冷凝器的无功发电/吸收，有载调压变压器的分接比以及补偿器的无功注入或吸收是决策变量。研究了ORPD问题，考虑了不同的运行约束，如支路、变压器抽头比和母线电压限制，以及发电机无功功率能力限制。

为了解决这些差距，本文介绍了一种更实用的多目标问题公式，包括风电综合电力系统的技术（降低电压稳定风险）和经济（包括无功发电成本和有功功率损耗在内的运营成本）目标。所有的技术不确定参数都包含在问题公式中。在所提出的公式中，对常规和风无功资源的实际限制进行了建模。

蒙特卡罗模拟（MCS）是利用不确定参数的适当分布函数来处理不确定参数。NSGA-II算法用于获得非支配解。应用模糊决策器方法从帕累托前沿选取折衷解。数值结果证实了该方法的性能。

1 技术分析

在不确定条件下进行风力发电系统的无功优化调度分析是一个复杂而重要的问题，主要包括以下几个方面：

1）风力发电系统的基本运行模型：风力发电系统由风机、风机转换器、电力系统等组成，需要建立系统的数学模型，考虑风速、风向、风机功率曲线以及电力系统的约束等因素。

2）无功功率的优化目标：无功功率的优化目标通常为提高风力发电系统的功率因数，减小无功功率损耗，稳定电网运行等。

3）不确定性建模和分析：在不确定条件下，风速、风向等因素是随机变量，需要建立相应的不确定性模型，例如使用概率分布描述风速的变化。

4）优化算法的选择：针对无功功率优化的问题，可以采用不同的优化算法，如基于模型的优化方法，基于遗传算法的优化方法，基于强化学习的优化方法等。

5）系统约束条件考虑：优化调度时需要考虑电力系统的约束条件，如电压稳定、潮流平衡、线损最小等约束条件。

6）随机性分析和评估：在不确定条件下，需要进行随机性分析和评估，例如采用蒙特卡洛模拟方法进行系统性能评估，评估无功功率的不确定性和风力发电系统运行的可靠性等。

不确定条件下，风力发电系统的无功优化调度分析是一个复杂的问题，需要综合考虑风力发电系统的基本运行模型、优化目标、不确定性建模和分析、优化算法选择、约束条件考虑，以及随机性分析和评估等因素。

2 多目标安全约束最优无功调度问题的求解

2.1 目标函数建立

文献中提出了不同的电压稳定指标来评估电压稳定裕度。这些指数根据以下内容进行了分类：

①基于雅可比矩阵和系统变量；②总线、线路和整体基础。

基于雅可比矩阵的VSI（电压稳定性指标）能够准确地计算电压不稳定点，但计算工作量很大。总线和线路VSI需要较少的计算时间，并且足以进行实时和运营规划。前文中提出的Lindex是众所周知的总线VSI之一。L指数定义为：

其中，Vi和Vj分别是总线i和j处的电压相量。F可计算如下：

L指数的值在0～1之间变化（电压崩溃点）。使用MCS的VSI的期望值可以计算为：

其中，n是MCS迭代次数。应最小化的电动车辆供电设备的最大值是拟定SC-ORPD中的电压不稳定风险或技术目标：

2.2 运营成本

在不考虑经济问题的情况下提高系统安全性，对于实际电力系统的运行和规划是不可接受的，所提出的公式的经济目标是运营成本，包括有功功率损耗和无功发电成本[3-5]。有功功率损耗成本可通过公式（6）计算：

LC是以元为单位的网络有功功率损耗成本；P是以元/MW为单位的有功功率损耗价格；NT-line线是T线的数量；gk是每条线的发送端和接收端的线路电导；δi和δj电压相位。本文假设P等于以元/MW为单位的平均有功功率成本。可以使用经济调度结果来计算P。

无功发电的成本取决于两个部分：①运营成本；②机会成本。先前的是由于发电机的无功发电或吸收而增加的绕组损耗的成本。机会成本是由于能力曲线限制而降低有功功率的成本。无功功率成本可以使用二次成本函数来表示。成本函数包括上述所有组成部分。这可以表示如式（7）所示：

Cq为发电机的无功成本；n为发电机的数量；Qgi单位为Mvar，指第i台发电机无功功率（产生或吸收）。是利用发电机能力曲线可以精确得到的系数。因此，运行成本（EVOC）的期望值可表示为：

3 不确定性建模及优化算法

3.1 不确定性建模

本文采用了双状态部件停运模型。图1显示了状态转换图。从数学上讲，每个组件的长期平均不可用性可以通过式（9）计算：

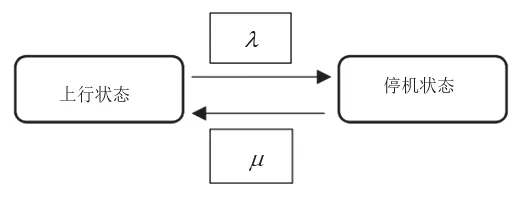
图1 可修部件的状态空间图Fig.1 State space diagram of repairable components

其中，λ为故障率（故障/年），μ为修理率（修理/年）。使用二项式分布对组件停机进行建模，成功率二项式分配是每个组件的可用性。可用性计算如下：

如果MCS随机过程在每次迭代中产生多个部件停机，以执行n-1应急分析，则将选择最可能的停机。

风力发电在很大程度上取决于风速分布。最常见的风的不确定性建模采用威布尔分布函数。这是由公式（11）给出的：

其中，c是缩放参数，k是形状因子。这些参数可以使用历史数据来计算，利用特性曲线可以计算出风速与风机输出功率之间的关系。线性化特性曲线如式（12）所示：

式（12）中：Pwind是风力发电机的输出功率，v是风速，单位为m/s；vcut-in和vcut-out为风机的切入和切出速度，单位为m/s；vrate是额定风速，单位为m/s。特性曲线如图2所示。

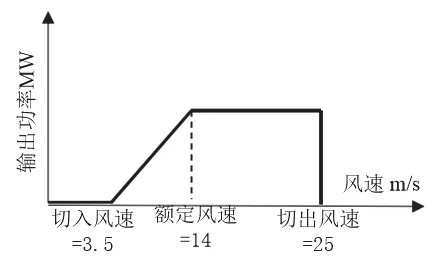
图2 风力涡轮机的功率曲线Fig.2 Power curve of wind turbines

节点负荷的不确定性使电力系统运行和规划中不可避免地存在需求不确定性模型。需求不确定性可以使用正态概率分布函数（PDF）进行建模。PDF特征可以使用历史数据获得。对于每个节点荷载，考虑一个独立的正态分布函数。假设负荷分布的平均值等于预测负荷，标准偏差为3%。

3.2 优化算法

在本文中，运用了一种具有改进的性能和快速非显性排序能力的NSGA更新版本（NSGA-II）。该优化算法被用于寻找被称为帕累托前沿（PF）的非支配解。

因此，需要另一种方法来选择折衷的解决方案。模糊决策者能够进行这种选择。该技术通过公式（13）对PF的每个成员使用隶属函数：

其中，Fi是第i个目标函数。使用最小-最大方法可以选择折衷解决方案。

4 仿真结果

所提出的公式在IEEE 30总线系统上使用软件进行了测试，通过在总线20中安装一个56MW DFIG风电场来修改标准测试系统。该算法在MATLAB R2017a中运行。表1中列出了计算发电机有功和无功功率成本所需的参数。

表1 发电机参数Table 1 Generator parameters

在这种情况下，本文讨论的所有技术不确定性都是在问题公式中公式化的。因此，每个MCS场景都包含单次停电，根据其适当的概率分布函数，使用支路的不可用性、风速和负载变化。

为了计算发电机的经济有功功率（作为SC-ORPD的初始条件）和有功功率损失成本，进行了经济调度。该初始条件也用于计算发电机的无功功率能力限制。根据EDC结果计算的预期总有功功率成本和预期有功功率损失成本分别为2317元和12.25元/MW。表2显示了发电机的预期经济有功功率以及发电机、DFIG和电容器的决策变量，用于折衷解决方案。表3显示了帕累托前沿的EVSI和EVOC范围及其使用所提出方法折衷解决方案的价值。

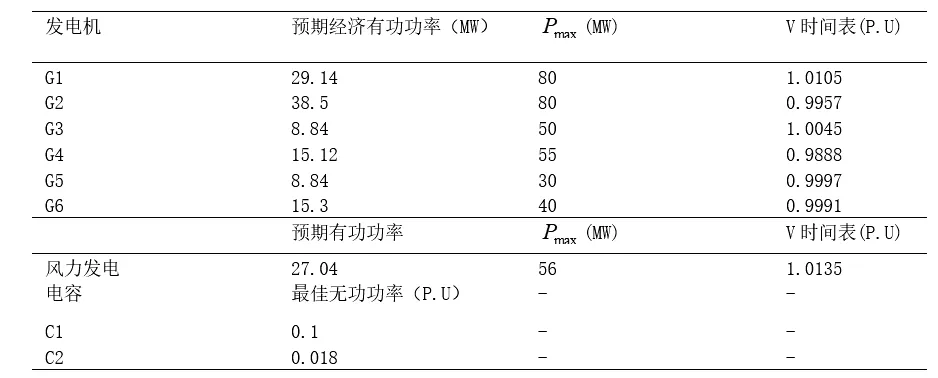
表2 发电机的预期经济有功功率Table 2 Expected economic active power of generators

表3 目标函数值Table 3 Objective function val ues

结果显示，当在MCS场景中对意外事件进行建模时，折衷解决方案的预期电压稳定裕度提高了34.4%。预计有功功率为4.34MW，成本为55.65美元。这意味着有功功率增加了，但发电机的经济运行降低了有功功率损失的成本。

运行成本达到44.89，很明显，为了增加电压稳定裕度，向系统注入了更多的无功功率。表3显示，大多数发电机的运行功率远远低于其额定功率。对发电机使用传统的无功功率限制将降低其向系统注入无功功率的能力。

因此，EVSI将增加。在这种情况下，如果考虑常规无功限制，则达到0.86。在这种情况下，总运营成本为2634元。无功功率成本不到总成本的10%。因此，该算法使用比有功功率便宜的无功功率来提高系统的电压安全性。由于电力系统的高X/R比，这也是可以接受的。计算时间是使用MCS的缺点，大多数模拟运行需要超过4000s才能达到停止标准。