基于时滞系统的模糊自适应容积卡尔曼滤波算法

黄晓姣，计甜甜，玉 姣，王文明

（皖西学院实验实训教学管理部，安徽 六安）

引言

现阶段，非线性滤波的问题普遍存在，比如在信号处理、目标跟踪等领域，针对非线性系统，该领域的研究者们提出了很多次优的滤波算法，主要包括扩展卡尔曼滤波（Extended Kalman Filter, EKF）[1]，无迹卡尔曼滤波（Unscented Kalman Filter, UKF）[2]，容积卡尔曼滤波（Cubature Kalman Filter, CKF）[3]，粒子滤波（Particle Filter, PF）[4]等，这些算法具备各自的优点，能较准确地估计目标的状态，但是它们也存在着不足之处，例如计算复杂度高、滤波精度低、误差太大等，所以相关的学者也提出了许多的改进方法，如自适应渐消有偏EKF[5]、矩阵加权自适应EKF[6]、Sage-Husa 自适应UKF[7]、改进自适应抗差CKF[8]等等。但随着非线性系统规模和复杂性的扩大，系统中通常会存在着噪声，同时受到外界各种复杂环境的影响，信号被传输的过程中，也会存在干扰、丢包等现象，导致量测模型出现时滞，所以对非线性滤波的性能还需要改进和提高。

我们对系统建立模型时，往往会假设系统噪声统计特性和量测噪声统计特性均为已知的，并且是均值为零高斯白噪声，其协方差矩阵在运动过程中不会发生变化，但事实不是如此，它们往往无法精确地确定，为此本节借鉴文献[10]的时滞转换方法和文献[9]的模糊CKF 方法，以容积卡尔曼滤波为基础，对同时具有观测时滞及量测噪声不确定的系统进行处理，提出了在观测时滞系统下的模糊自适应容积卡尔曼滤波算法，通过仿真验证，该算法可以有效减小误差且提高滤波精度。

1 模糊自适应CKF

首先介绍一下模糊推理系统。模糊推理系统[9]也称为模糊控制。如图1 所示，一个模糊推理系统基本包括5 个功能块。

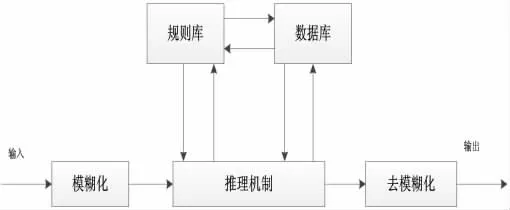
图1 模糊推理系统

考虑如下离散时间非线性系统

式中，x为系统的状态向量；zk为量测值和为非线性函数，为系统过程噪声，v为量测噪声。滤波时，都是假设和vk相互独立，且分别是零均值，协方差为Q和的高斯白噪声，但量测噪声方差易被影响，因此，对于CKF 要具备自适应调节的能力[11]。

在CKF 的整个滤波过程中，其系统残差可以表示为

则系统残差方差实际值可表示为

式中，M 为根据经验选取的平滑窗口。

根据式

系统理论残差方差为Pzz，定义两者迹的比值为

若系统噪声统计特性准确，αk应该在1 附近[12]，当系统测量噪声的实际值与先验值存在差距时，αk将偏离1，为了使其稳定，通过调节对理论残差方差进行修正，即

式中：εk为调节因子，εk可以根据模糊推理系统计算得到，以αk作为模糊推理系统的输入，εk为其输出，以1 为参考，设S 表示模糊集合“小”，M 表示基本等于1，L 表示模糊集合“大”，可建立如下模糊推理规则：

（1）如果αk∈S，那么εk∈S；

（2）如果αk∈M，那么εk∈M；

（3）如果αk∈L，那么εk∈L。

系统框图如图2 所示。

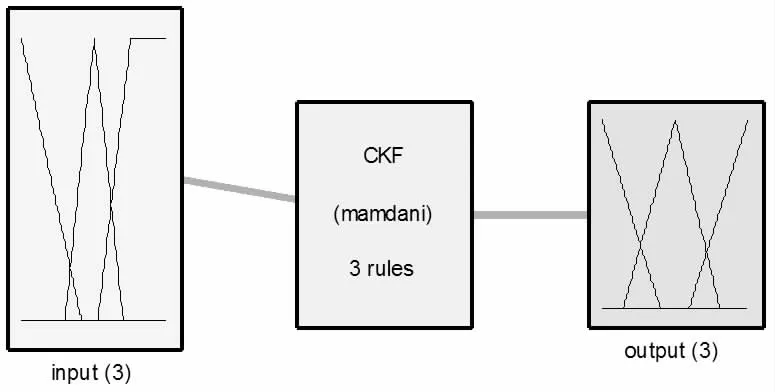
图2 模糊推理系统框图

αk与εk的隶属度函数分别如图3、图4 所示。

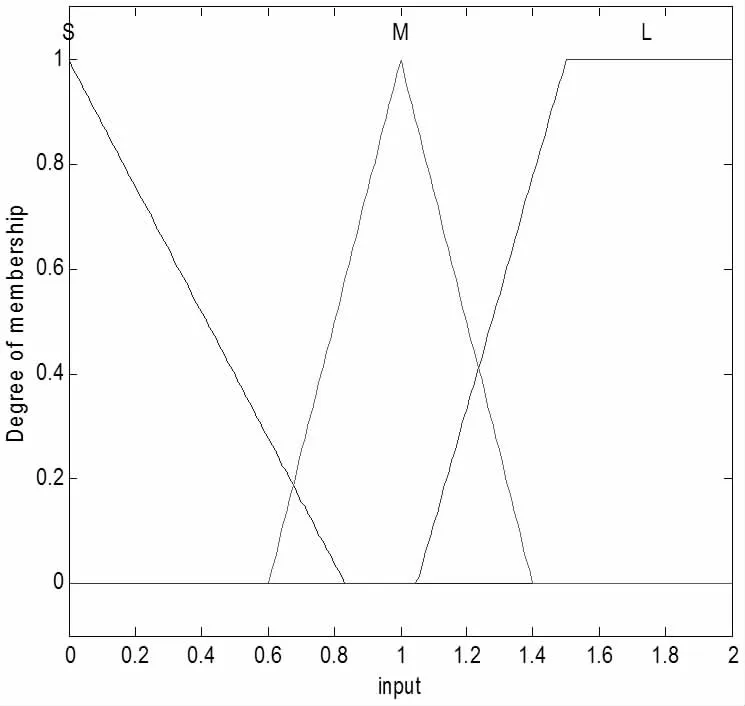
图3 输入αk 的隶属度函数

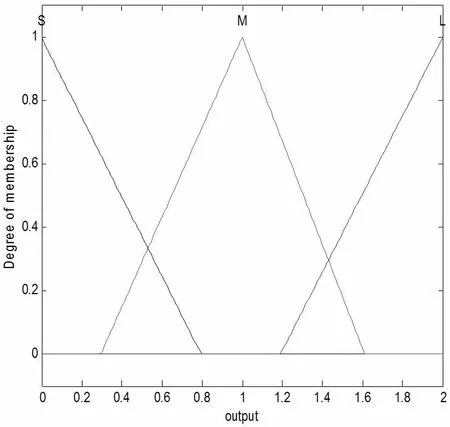
图4 输出εk 的隶属度函数

对于去模糊，算法中用解重心法得到精确的值，即

其中，θj为图4 中对应3 个模糊集的隶属度；Sj为各个模糊集的中心。

将模糊推理系统每一步运算得到的εk代入式（6），对进行自适应调节。

2 观测时滞系统

通常情况下，非线性观测时滞系统的方程可以表示为：

其对应的矩阵方程可表示为：

其中，Yk和分别是k 时刻和k-1 时刻的增广状态向量；和Vk=vk-r分别为引入增广状态之后的过程噪声和观测噪声。式（10）符合滤波算法的系统方程，只是维数变大，对式（11）重新定义，则式（10）、（11）描述的观测时滞系统可表示为：

式中：f*（·）、h*（·）- 与式（12）、（13）相同的非线性映射关系；Uk、Vk- 引入增广状态之后的过程噪声和观测噪声，方差分别是且相互独立，，

3 观测时滞系统下的模糊自适应容积卡尔曼滤波

综合前面对观测时滞和量测噪声不确定情况的处理，将观测时滞系统下的FACKF 算法基本步骤归纳如下：

（1）用状态增广无时滞模型对式（8）、（9）表示的带观测时滞且量测噪声不确定的非线性系统进行处理，成为式（14）、（15）；

（2）经变换后的式（14）、（15）符合卡尔曼滤波的标准形式，量测噪声和变换之前一样具有不确定性，可用精确度较高的模糊自适应CKF 算法对其进行处理；

a.对X0，P0|0及量测噪声的方差R0进行初始化，设定平滑窗口M 的值；

b.进行第一个平滑窗口内的M 步CKF 计算（k=0，…，M-1）；

c.通过式（2）～ 式（6）计算系统残差ηk、系统残差实际值和残差实际值与残差理论值的比值αk；

d.以αk为FIS 的输入，通过模糊系统计算量测噪声方差Rk的调节因子εk，并利用εk对Rk进行调节；

e.令k=k+1，用调节后的R替换原有的完成CKF滤波；

f.重复执行步骤c～步骤e。

（3）步骤（2）已经对变换后的标准形式运用CKF 进行了滤波处理，且量测噪声运用模糊算法得到了很好的处理，再根据前r个时刻的状态值Y0，…，Yr和方差Pr，递推计算出k时刻的增广状态值，进而得到状态估计就是观测时滞的状态估计；

（4）算法结束。

4 仿真验证与分析

采用角测量跟踪模型，该模型普遍用于雷达目标跟踪的仿真验证中。假设目标做匀速直线运动，且把时滞系统处理过后，得到的增广状态用如下模型仿真：

式中：Φ 为状态转移矩阵；Γ 为状态噪声驱动阵；N为采样时间；T 为采样间隔；是系统状态变量。其中：

假设系统初始状态为x0=（220，1，55，-0.5）T，T=3s，N=1000s，初始方差阵设调节因子εk的指数b 取1.2，平滑窗口宽度M 取10。用容积卡尔曼滤波（CKF）和本文进行仿真比较，并使用均方根误差（RMSE）评价算法性能，仿真对比如图5 和图6 所示。

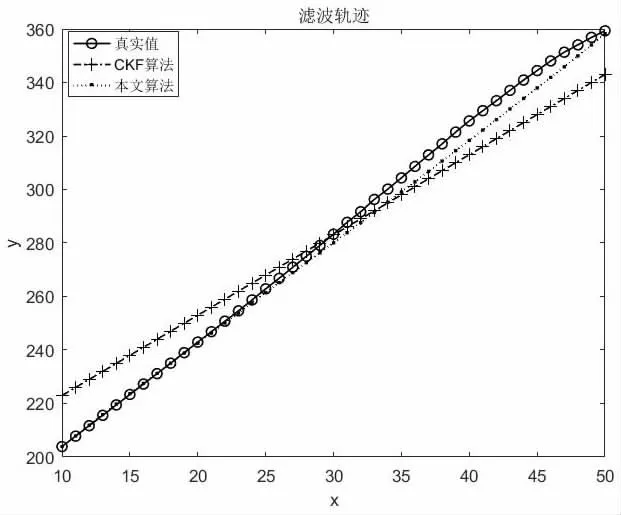
图5 目标轨迹对比

图6 滤波误差对比

从图5 可以看出，本文的算法和真实轨迹更接近，图6 得出的误差也相对更小，因此本文在前人基础上改进的算法效果稍优。我们不能否认每种算法都有其一定的优越性，在不同的阶段，针对不同的问题，但是我们在优越算法的基础上改进与创新，使之更优越，才是我们的最终目的。

5 结论

本文提出了一种具有更高精度的基于时滞系统的模糊自适应容积卡尔曼滤波方法。该算法把系统状态增广时滞转换方法和模糊自适应调整量测噪声协方差阵权值的方法相融合。仿真结果表明该算法可以有效减小误差且提高滤波精度，具有更优的估计性能。