基于聚类算法的电网告警数据分析与处理模型*

刘 波，万维威，邹大均，李 立

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

目前，全球网络安全形势日益严峻，针对关键信息基础设施的恶意网络攻击频发。随着负荷侧资源不断扩充，电力监控系统的安全防护范围不断扩大，接入安全显得尤为重要。随着安全防护范围的不断拓展，产生的安全数据日益倍增，告警数量不断增大，如何确保告警及时有效，提升告警的精准度和实效性，成为安全防护监管的一大难题[1]。

大量学者对智能告警技术开展了深入研究。其中，有研究利用K-近邻算法（K-Nearest Neighbors algorithm，KNN）、卷积神经网络（Convolutional Neural Network，CNN）等机器学习或人工智能算法对电网大数据进行清洗，并采用典型建模方法分析安全事件，实现对电网数据的智能处理[2-5]，但是这些算法需要占用一定的计算空间。此外，还有研究基于规则、模型等基本数据，采用层次分析法等方法得到当前告警信息特征并进行分层分类，为更具价值的数据分配更高权重[6]，但此类方法需要多名专家对数据的重要性进行评价，使用起来较为 烦琐。

针对上述问题，本文使用K-Means[7]和DBSCAN[8]算法，以电力监控系统网络安全管理平台的历史告警数据为处理数据，提取告警数据特征信息，进行多维度的特征聚类，最终建立电力监控系统网络安全事件告警数据综合分析模型，提高已有分析系统的效率。

1 算法描述

1.1 K-Means 聚类算法

作为经典且应用广泛的聚类算法之一，K-Means 聚类算法具有的优点有理论可靠、算法简单、收敛速度快、能有效处理大数据集等。K-Means算法中的K 代表类簇个数，Means 代表类簇内数据对象的均值。K-Means 算法是一种基于划分的聚类算法，以距离作为数据对象间相似性度量的标准，即数据对象间的距离越小，它们的相似性越高，则它们越有可能在同一个类簇。

具体的聚类过程如下：

算法1：K-Means 算法

1.2 DBSCAN 聚类算法

DBSCAN 基于一组邻域来描述样本集的紧密程度，参数(ε,MinPts)用来描述邻域的样本分布紧密程度。其中，ε描述了某一样本的邻域距离阈值，MinPts描述了某一样本的距离为ε的邻域中样本个数的阈值。

DBSCAN 算法的具体聚类过程如下：

算法2：DBSCAN 算法

2 电网告警数据分析与处理模型

本文提出的电网告警数据分析与处理模型，分为基于时间的K-Means 聚类和基于特征关键词的DBSCAN 聚类。第1 步主要使用K-Means 对输入的原始告警日志数据进行压缩，依据的条件为日志数据中的时间信息，包括告警数据最新发生时间和告警开始时间。第2 步则提取前一步压缩后数据的特征，根据特征关键字使用DBSCAN 算法进行进一步压缩。最终实现对电网原始告警日志数据的压缩与聚类，建立电力监控系统网络安全事件告警数据综合分析模型，并根据聚类的结果对告警数据进行分析和研判，给出每一类告警信息的具体描述，提高现有电网告警数据分析系统的效率。模型的具体流程如图1 所示。

2.1 基于时间的K-Means 聚类

分析原始告警日志数据可以发现，现有的电网告警系统根据告警数据的各项属性对原始数据进行了具象化描述。对于任意一条告警数据s，根据属性可以将其划分为告警级别、告警内容、告警设备、上报设备、告警开始时间、最新发生时间、告警次数、上报状态、日志类型、日志子类型和告警状态，具体可以描述为s（level,content,dev_ale,dev_up,time_beg,time_new,count,status_up,type_main,type_sub,status_ale）。使用K-Means 算法可以根据任一属性对原始数据集进行聚类，但实际聚类效果有所不同，最终进行描述时所依据的属性也会存在差异。本模型主要从告警数据的时间维度出发，考虑原始告警数据集中的告警最新发生时间S.time_new 和告警开始时间S.time_beg，最终聚类完成后将时间维度作为信息描述的一个重点。基于告警数据中时间属性的K-Means 聚类如图2 所示。

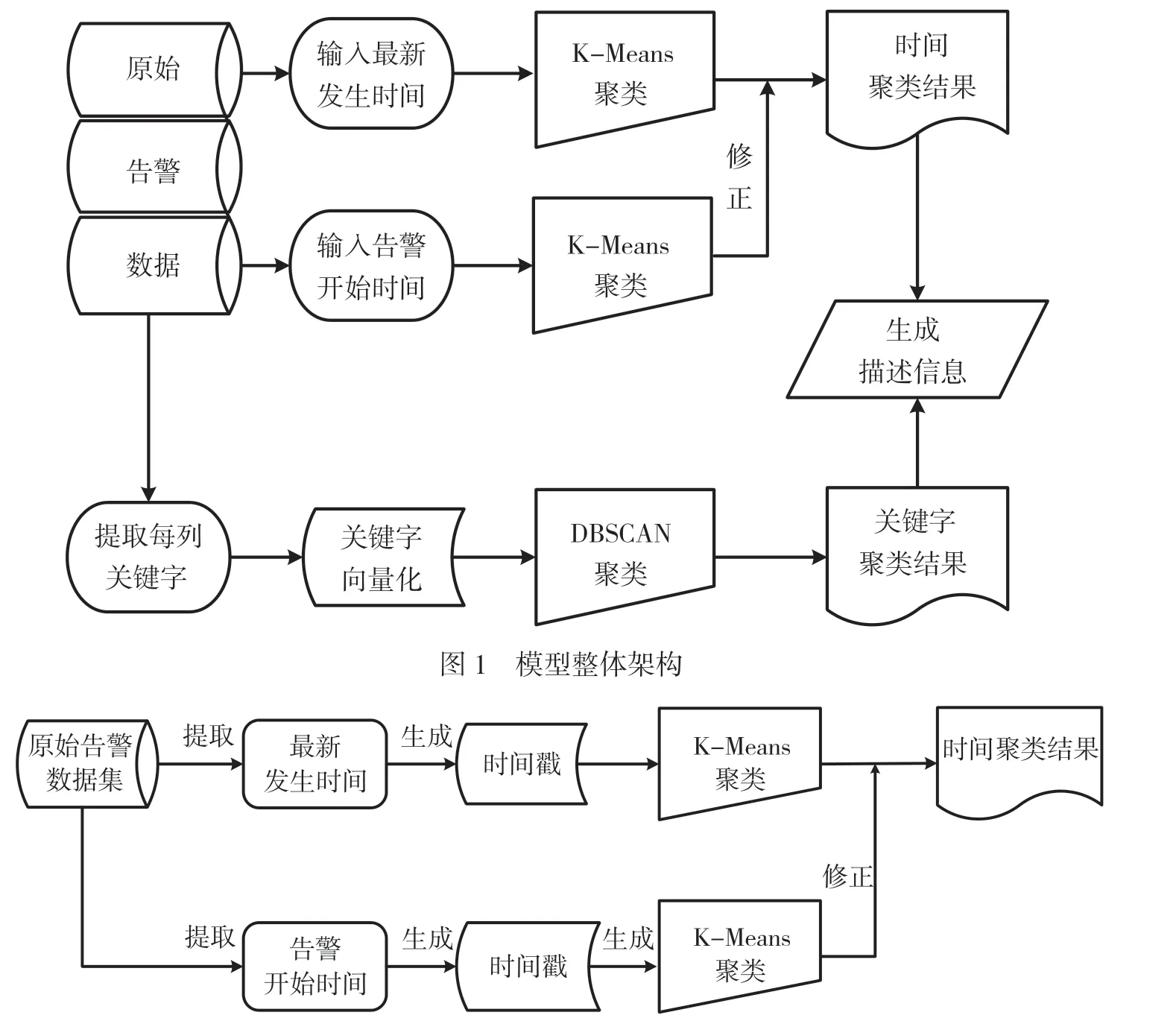
图2 基于时间属性的K-Means 聚类

此外，在进行两次K-Means 聚类时，还需考虑初始的K值选取。K值的不同会极大地影响聚类的效果，具体K值的选取需要考虑聚类后时间维度的准确率。此处进行K值选取的规则定义：在对原始数据集的时间维度进行分析的基础上，给出聚类后各类别的预期时间跨度Tk，即当按照某个K值对原始数据的时间维度进行K-Means 聚类后，每个类中的时间跨度都满足tk≤Tk，此时称时间维度的K-Means 聚类达到最优效果。同理，对K值选取时对应的准确率Acck定义如下：对于时间维度的K-Means 聚类，准确率Acck指聚类后满足tk≤Tk的类别数量与所有类别数量的比值，即满足预期时间跨度要求的类别与总类别的比值。原始数据集的时间跨度、聚类后各类别的预期时间跨度Tk、不同的初始K值都会影响聚类后时间维度的准确率，因此需要通过具体实验来确定最优的参数进行K-Means 聚类，使聚类的压缩率和准确率达到相对最优的结果。

2.2 基于特征关键词的DBSCAN 聚类

在进行DBSCAN 聚类之前，需要将3.1 节中聚类后的结果进行基于关键词的向量化操作，因此需要对S.level、S.content 等告警数据的属性进行分析，给出关键词向量化的基本规则。由于告警设备以及上报设备差异性较小，并且并非最终关联性描述时的元素，因此直接用固定的数值代替S.dev_ale 和S.dev_up 两个属性原始字符串内容，其他7 列属性的关键词向量化规则如表1 所示。

表1 关键词向量化规则

使用正则化表达式对原始数据集中每条日志数据进行关键字搜索与匹配，接着根据上述规则将关键词所在列转换为数学向量，同时将S.dev_ale、S.dev_up、S.time_beg 和S.time_new 这4 列直接转换为固定的数字，用于保证整体数据的规格统一。

3 实验及结果分析

3.1 实验数据集与参数设置

选取电力监控系统近一个季度的历史告警数据，分为30 个地市，每个地市的数据单独存储，总条目数为4 739 条。实验先基于最新发生时间，使用K-Means 对原始数据集进行聚类。以其中某地市的告警数据为例，该地市近一季度的告警数据总条目数numb为108 条，最新发生时间的时间跨度为2021.08.29 05:28:48—2021.11.27 18:39:04，则初始K值的选取方法为：获取最新发生时间的时间跨度时间戳形式为1 630 186 128～1 638 009 544，因此时间跨度T=1 638 009 544-1 630 186 128=7 823 416。根据要求设定聚类后各类别的预期时间跨度Tk为（2.5,3）天，时间戳形式下Tk为(216 000,259 200)，同时规定K的范围为[10%×numb,30%×numb]。对于该地市，即K属于[10.8,32.4]，并且K为正整数。同理获取告警开始时间的时间跨度，给出对应的K值 范围。

通过多次实验验证K的取值与准确率Acck之间的关系，具体实验结果如图3 所示。

图3 最新发生时间和告警开始时间的K 值与准确率的关系

由图3（a）可知，当K值选取20 时，针对该地市的最新发生时间进行K-Means 聚类，可以达到最高的准确率，使得聚类后准确率达到97%。由 图3（b）可知，当K值选取19 时，针对该地市的告警开始时间进行K-Means 聚类，可以达到最高的准确率，使得聚类后时间跨度满足要求的类别数与总类别数的比例达到97%。

使用Calinski-Harabaz 指标（简称CH 指标）对K的取值进行验证，CH 指标通过类间方差和类内方差之比计算得分，得分越大表示效果越好。对最新发生事件的K值进行CH 指标计算，由图4（a）可知，K值选取20 或30 左右时，CH 指标值相较于其他K值数值较大。综合图3（a）和图4（a）的结果，选取K=20 作为针对该地市的第1 次K-Means 聚类。

图4 最新发生时间和告警开始时间的K 值与CH 指标的关系

由图4（b）可知，第2 次基于告警开始时间的聚类，K大于或等于19 时可以达到最高的准确率和较好的聚类结果。综合图3（b）和图4（b）的结果，选取K=19 作为针对该地市的第2 次K-Means 聚类。

实验第2 阶段采用DBSCAN 算法。对于该地市的数据，考虑邻域半径ε与噪声率之间的关系，进行多次实验，最终得到的关系如图5 所示。

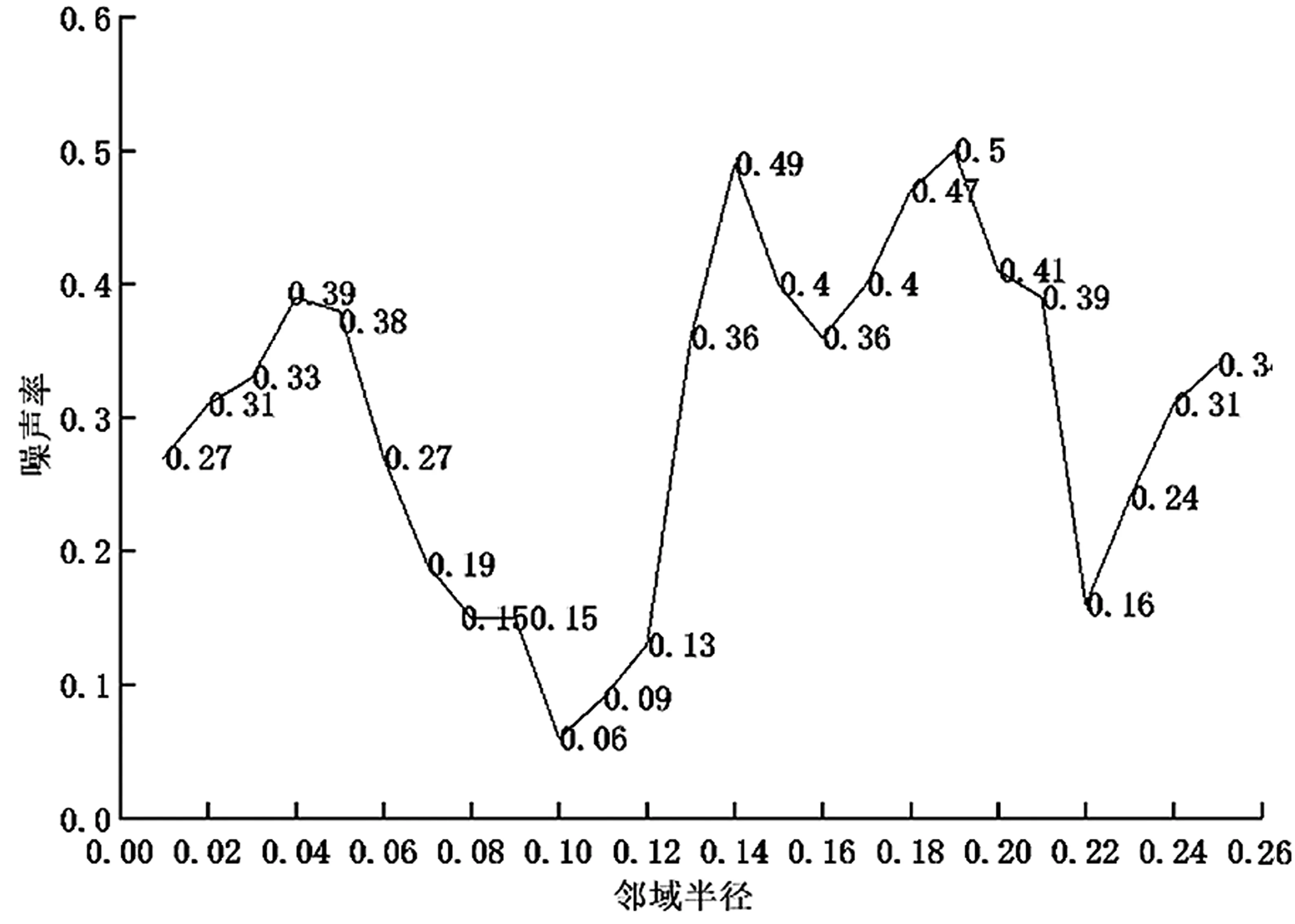
图5 邻域半径与噪声率的关系

由图5 可知，DBSCAN 聚类选取0.1 作为最优的邻域半径ε，而邻域中数据对象数目阈值MinPts则为每个地市单独文件下日志子类型的种类数量，此时进行DBSCAN 聚类可以达到最优效果。

3.2 评估指标

实验对于聚类结果的评价，主要采用以下3 个指标。

（1）压缩率（Compression rate）。压缩率指聚类后数据形成的类数量与聚类前所有条目数量的 比值。

（2）噪声率（Noise rate）。噪声点指未成功完成聚类的条目，噪声率指聚类后出现的噪声点数量与聚类前所有条目数量的比值。

（3）准确率（Accuracy）。准确率指聚类后满足tk≤Tk的类别数量与所有类别数量的比值，即满足预期时间跨度要求的类别与总类别的比值。

由上面的定义可知，压缩率越高、噪声率越低、准确率越高的聚类结果是最优结果。

3.3 实验与结果分析

按照上述方法，首先对输入的某地市近半年告警数据进行聚类，采用K-Means 聚类算法，统计该地市告警数据文件中数据条目数numb为108 条，计算初始K值为20。接着基于告警数据的最新发生时间进行K-Means 聚类，具体过程为：提取每条数据的最新发生时间并转化成标准时间形式，再生成对应的时间戳，接着选取20 个不同的时间戳作为初始聚类中心，对任意一条数据，求其时间戳到20 个聚类中心的距离，将其归类到距离最小的中心的聚类。不断迭代并在每次迭代过程中利用均值法更新各聚类的中心点，最终将所有108 条数据进行聚类，分为20 大类，作为K-Means 第一次聚类的结果。聚类结果如图6 所示。

图6 基于告警数据最新发生与开始时间进行聚类的结果

图6（a）为基于告警数据最新发生的聚类分布，分析发现，依据最新发生时间进行聚类时，存在部分数据告警开始时间相同但未处于同一类的情况，主要原因是第一次聚类只考虑了最新发生时间这一属性，而未考虑告警开始时间，因此在时间维度上还有优化空间。基于告警数据的开始时间进行K-Means 二次聚类，此时输入数据集依旧为该地市对应的告警数据原始文件，K值选取19。聚类结果如图6（b）所示，可以发现二次聚类能够修正第一次聚类后出现的异常情况，并且压缩率更高。最终汇总K-Means 两次聚类的结果，作为第一阶段K-Means 的输出。

模型第二阶段利用DBSCAN 算法对告警数据的关键字维度进行再次聚类，首先按照3.2 节的关键词向量化规则，对该地市所有数据进行向量化操作，其次设置邻域半径ε为0.1，邻域中数据对象数目阈值MinPts为该地市告警文件中日志子类型的种类数量4。在对输入维度进行降维操作之后，对聚类结果进行可视化，结果如图7 所示。从聚类结果可以看出，在所有的108 条数据中只存在7 个噪声点，意味着只有7 条数据没有完成 聚类。

图7 DBSCAN 聚类结果

采用同样的方法对该省其他29 个地市的告警数据进行聚类分析，最终得到所有地市的聚类情况如图8 所示。30 个地市中，有19 个地市的压缩率达到20%以下，30个地市的压缩率都达到30%以下，平均压缩率为23.62%。准确率方面，27 个地市都达到80%以上，平均准确率为88.34%。噪声率方面，25 个地市都低于20%，平均噪声率为15.06%。

图8 30 个地市的聚类结果

最后基于聚类后的结果，采用关联性结果描述，具体描述的信息为：某地市的第××条至××条日志在yyyy-mm-dd hh:mm:ss 至yyyy-mm-dd hh:mm:ss 期间内发生了××事件，即根据日志最新发生时间和日志子类型的聚类结果，分段描述告警数据的具体信息，具体实例如下文所示。

（1）第1 条日志在2021-08-29 05:28:48 时刻发生了主机开放危险端口事件；

（2）第2 到6 条日志在2021-09-01 18:39:04至2021-09-01 21:18:10 期间内，发生了USB 存储设备接入；

（3）第7 到12 条日志在2021-09-04 21:26:10至2021-09-04 21:31:42 期间内，发生了数据网危险端口访问；

（4）第13 到18 条日志在2021-09-16 20:47:55 至2021-09-18 12:11:15 期间内，发生了USB 存储设 备接入、数据网危险端口访问；

（5）第19 到26 条日志在2021-09-23 09:28:47 至2021-09-24 10:31:09 期间内，发生了数据网危险端口访问、串口访问。

后续结果与上述描述类型一致，具体内容不再列出。

从结果可以看出，综合K-Means 和DBSCAN算法的结果，能够对原始告警数据进行高效压缩，并给出每个时间段内具体发生的告警事件类型，大大降低了原始数据的复杂度以及阅读难度，提高了对于告警数据关键信息的抽取能力。

3.4 算法对比试验

为了展示本模型对电网告警数据分析处理的优势，本文进行了K-Means 时间聚类配合DBSCAN关键字聚类与经典DBSCAN 聚类的对比试验。从数据集中随机抽取了一个电站的告警数据，共32 条。首先在选取合适的参数后，对告警数据按照本模型进行K-Means 时间聚类配合DBSCAN 关键字聚类，输出第一次聚类结果；其次将两个时间维度加入DBSCAN 聚类的输入当中，选取与第1 次聚类相同的参数，得到第2 次的聚类结果，两次聚类结果的噪声率结果如表2 所示。

表2 两种算法噪声率对比

4 结语

本文首先建立了电力监控系统网络安全事件告警数据综合分析模型；其次选取了真实的电网告警数据进行实验；最后通过对不同类别的告警数据进行多维度聚类降维，寻找到多维数据间的统计特征，最终通过压缩率、噪声率及准确率等指标对模型的聚类效果进行评价。实验结果表明，本文所建立的模型可以快速准确地抽取出大量告警数据的统计特征，并对数据进行降维压缩，在K-Means 的压缩率、DBSCAN 的噪声率及两者结合的准确率上都有较好的表现，解决了现有告警系统数据杂乱、关键信息难以提取等问题，极大地提高了电网告警系统分析和处理数据的能力。