大规模星座组网通信的多址接入方式优化

郭晓旭, 徐兆斌,2,3, 徐可笛, 朱耀伟, 金仲和,2,3

1.浙江大学微小卫星研究中心， 浙江杭州 310027；2.浣江实验室， 浙江诸暨 311899；3.浙江省微纳卫星研究重点实验室， 浙江杭州 310027

自20世纪末以来,随着航天技术特别是卫星技术的发展与进步,卫星星座及编队技术因其广覆盖、低延时、高效性等优势开始逐渐被重视[1],除了已经发射使用的铱星星座、GPS、北斗卫星导航系统等星座任务外,许多科研机构与航天集团已经逐步组织、计划或开展了大规模星座的组网和发射计划,例如SpaceX公司已经在逐步推进其42 000颗卫星的Starlink超大规模低轨星座计划,OneWeb公司计划部署2 000多颗卫星分布在低轨上,Telesat公司也提出规模约为298颗卫星的Lightspeed星座计划,国内航天科技集团也提出了发射300多颗低轨组网卫星的“鸿雁”系统[2]。在这些大型星座的组网通信中,建立足够多的地面信关站显然是不现实的,因此卫星要协同完成任务,用于组网通信的星间链路建立是必需的,而超大规模星座其庞大星间链路的建立则需要一种切实可行的多址接入方式。

目前说来,常用的卫星多址接入方式包括预约多址接入、竞争式多址接入和预分配多址接入[3],其中预约多址接入是每个用户在进行传输前对所需时频资源进行申请,申请应答后再进行传输,故该多址方式流程较长,当卫星节点增加时,该方法的通信效率与通信即时性会大大下降。竞争多址接入方式是用户在有信息传输需求时即可进行传输,所以当星座中的卫星容量上升时,用户信息冲突可能性较大。预分配多址接入则是提前为每个用户预先分配时间和频率资源,用户在信息传输时只占用固定资源而不会互相冲突,典型技术包括时分多址(time division multiple access,TDMA)、频分多址(frequency division multiple access,FDMA)以及码分多址(code division multiple access,CDMA)技术。其中TDMA技术需要卫星提前完成时间同步,在大规模星座中该技术将严重限制卫星的组网通信效率。FDMA技术则需要每个卫星占有独自的频谱资源,在卫星频谱资源匮乏的情况下该方法亦不适用于组网通信。而CDMA技术应用于超大星座的组网通信时则会出现多通道干扰与码组容量不足的弊端。综上所述,时频资源的紧缺严重制约着星座容量的扩展,而目前的多址接入方式已经逐渐无法满足超大规模星座的组网通信需求,因此亟需对大容量组网通信的多址接入新方式进行探究,从而尽量提高卫星时频资源利用率以面对未来大规模星座广泛铺设的应用环境。

为了对适应星座组网的多址接入方式进行探讨,本文首先以稀疏码分多址技术(sparse code multiple access,SCMA)为核心构建了星间稀疏扩频通信系统,提出使用枚举遍历算法进行码本设计,在通信帧中添加适时引导序列,并在接收端利用迭代矫正算法对信道参数进行估计。系统建立后本文对超大规模星座的通信信道特点进行分析并在MATLAB中建立对应模型,最终在建立的星座信道模型中对稀疏扩频通信系统进行了性能仿真与分析。

1 星座组网稀疏扩频通信系统

一般说来,常用的星间链路通信系统其发射端通过编码、调制、上变频等步骤将业务数据处理后进行传输。例如目前卫星通信中常用的码分多址技术,它通过伪码序列将每个卫星的业务数据进行频谱拓展,不同卫星的伪码序列彼此正交,这样才能保证通信系统的接收端能够通过伪码序列的相关性实现多用户检测,但是当星座或编队中的卫星节点数大于扩频增益时,正交的伪码序列则会数量不足,这一弊端限制了CDMA技术的用户容量。SCMA技术则是将调制与扩频技术结合,将业务数据映射为复频域的多维稀疏码字,并通过多用户节点复用有限子载波来提高时频利用率[4]。图1给出了以SCMA技术为核心建立的星座组网稀疏扩频通信系统结构。在该系统中,多颗卫星的业务数据首先通过信道编码以提高其信息传输的可靠性,然后通过SCMA技术映射为复频域数据,最终通过射频链路形成传输信号。信号经自由空间传输后到达接收端卫星,接收端将信号下变频为基带信号,并通过多用户检测算法消除卫星间干扰,最终通过信道解码器还原卫星传输的业务数据,以此方式建立多卫星间的通信链路,从而完成组网操作。

图1 星座组网稀疏扩频系统示意

1.1 多址映射与译码原理

稀疏扩频通信系统在发射端完成卫星的业务数据映射工作,其中核心的SCMA技术将QAM(quadrature)调制与扩频融合在一起,发射端为每颗卫星设计特有码本,并根据码本将卫星的通信数据直接映射为码字[5]。

图2展示了一种用户数V=6,子载波资源块数K=4的SCMA映射结构。当用户进行数据传输时,系统依据用户的码元数据和特有码本选取码字,并将不同用户的码字进行叠加后传输。如当用户4发送“11”数据时,系统挑选用户1的第4个码字与其他用户的码字进行叠加,以此类推。因此,SCMA映射规则可以概括为:

图2 SCMA码字叠加过程

f:Blog2M→χi,xi=f(bi)

(1)

式中:M表示用户传输的码本宽度;bi∈Blog2M表示用户传输的码元数据;xi表示用户的码字;χi表示用户特有的码本[6]。,可利用资源块星座图更直观地表示整个SCMA的映射过程,图3给出了资源块1的星座图叠加过程,使用资源块1的用户2、用户3、用户5分别进行映射后最终形成该资源块的星座总图[7]。

图3 SCMA星座资源图

SCMA完成了上述的码本映射后,通信数据通过模拟射频链路被上变频至通信波段,经过自由空间传输后到达接收端,可将传输的信道模型简化为hv,其中v为不同用户的顺序,则经信号传输与多用户叠加后,接收端收到的信号可以表示为

(2)

式中:xv表示第v个用户的码字;n为高斯加性白噪声,即n～CN(0,N0I)。

稀疏扩频通信系统接收模块可利用接入码字的稀疏性进行多用户联合检测以恢复指定卫星的码元数据,多用户检测一般使用消息传递算法(message passing algorithm,MPA),而消息传递算法的原理就是利用先验信息和图模型结构完成对外概率和后验概率的估算[8]。通过不断更新用户节点(user nodes,UNs)与资源节点(resource nodes,RNs)之间的传递信息,实现算法残差修正,进而提高译码检测性能。图4给出了消息传递算法循环过程,其步骤可简述如下:

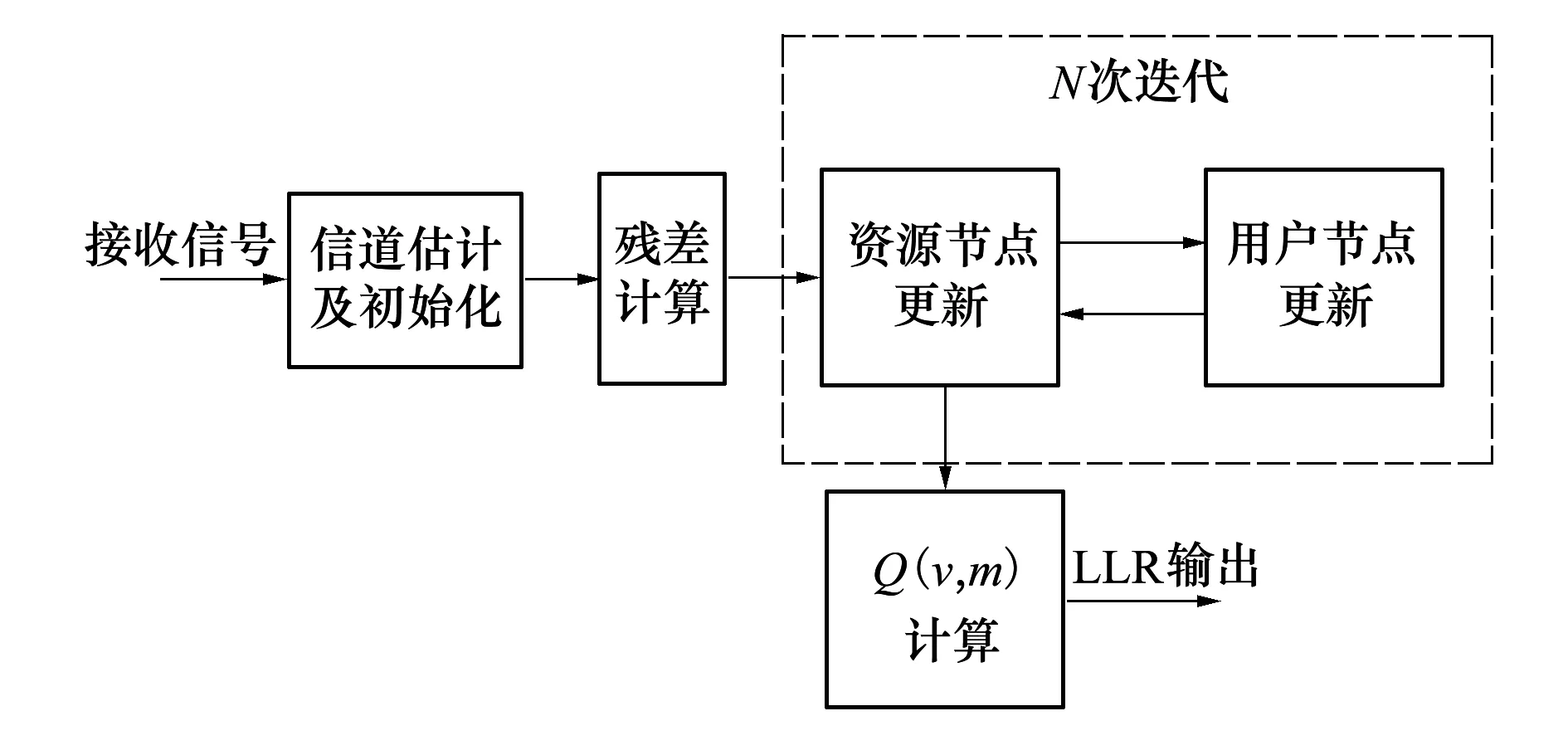
图4 MPA算法过程

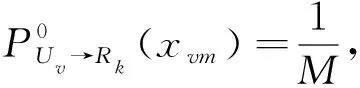
(3)

式中:N0为信道噪声功率谱密度;yk为第k个资源节点的传输信号;hk,v为信道冲击响应;xk,v为第k个资源块上的用户码字信息,资源节点通过Mk(xk)更新自身的信息概率

(4)

(5)

不断重复上述2步迭代,在多次运算后信息概率将趋于收敛,代表多用户信息检测基本完成,输出码元数据的似然比(logarithm likelihood ratio,LLR),此时通信系统接收模块可译出指定卫星的码元信息[9]。

1.2 系统核心算法

在将SCMA多址技术应用于星间时,其算法可具体分为发射端多址映射算法与接收端译码算法。

在卫星发射端多址映射算法中,各卫星根据稀疏扩频码本将需发送的业务数据一一映射,因此发射端算法中的核心即为稀疏码本的设计。在发射端,当一个资源块上承载的第一个用户的稀疏码本固定后,其他用户的码本为前一用户的码本依次乘以旋转因子θ得到,该操作在星座图中则可看做对星座点进行角度为θ的旋转。在星座图中,定义星座点间的归一化最小欧氏距离为

(6)

步骤1 设置资源块数K、每个资源块上承载的用户数Vk、旋转因子遍历步进θstep;

步骤2 初始化使用资源块k的第一个用户码本xk,1;

θi=i·θstep

forv=2 toVK

xk,v=ejθixk,v-1

end for

计算星座点间的欧式距离ρi

ifρi≥ρi-1

θopt=θi

end if

i=i+1

End for

步骤4 令k=k+1,并重复步骤2～3,直至得到各个资源块上合适的码本分布。

发射端完成多址映射后,卫星的接收端通过消息传递算法完成多用户检测。目前说来,对于MPA算法的研究已经较多,且研究大多围绕简化其迭代算法开展[11-14],但在MPA的算法模型中皆假设其信道传输矩阵是已知的,对于星间通信系统这显然是不现实的。卫星间通信链路具有时变性,且卫星终端不能像地面基站一般对信号进行高精度大规模的综合处理,因此通信链路中每个用户的信道参数hv无法提前获取,但获得准确的信道传输矩阵是进行多用户传递算法的先决条件。本文在通过发射端添加适时引导序列,并在接收端依据引导序列的接收信号进行信道估计的方法来获得每个用户的信道传输参数hv。

图5给出了本文建立的星间系数扩频系统的数据帧结构,每一包数据由引导序列与业务数据组成,每一帧的引导序列格式相同。卫星接收端收到当前数据帧后根据引导序列进行信道估计,信道估计利用迭代矫正算法,以资源块1为例,其迭代公式为

图5 系统数据帧结构

(7)

2 星座信道模型建立

信道作为信号传输的媒介,是通信结构的重要一环,信道质量最终也对通信系统性能有决定性影响。大规模星座的星间通信链路亦是如此,星间链路信道中产生的衰减、随机干扰、多径干扰、噪声、时延以及多普勒频偏都会对通信质量产生影响。对稀疏扩频通信系统来说,通信链路中的干扰和频偏等影响会让星座图各点发生位移和旋转,噪声则会让星座图点发生弥散,上述影响使星座图各点之间欧氏距离产生变化,从而使得系统的通信性能下降[15]。

为了对稀疏扩频通信系统在星间链路信道中的应用进行仿真,首先要对星间信道进行模拟,建立接近实际情况的理论信道模型以进行通信系统的性能评估。目前来说,对于卫星信道的探讨大多都集中于星地信道,在少数关于星间链路信道模型的研究中,文献[16]对中继卫星和地面终端的信号传输、多径效应、阴影效应进行了分析,但其信道模型局限于星地通信;文献[17]利用STK软件对星间太赫兹通信进行了模型建立,但其研究波段仅局限于太赫兹波段;文献[18]则只是在瑞利信道下对SCMA系统的误码率进行了仿真分析。因此,对于星座的星间信道建模分析来说,上述研究都存在着一定的局限性,针对此,本文将对卫星星座或编队中的星间信道各项影响因素进行深入探究,并分析建立信道模型。总体来说,星间信道对信号存在着衰落和噪声影响,而衰落可分为大尺度衰落和小尺度衰落,在星间链路中大尺度衰落主要是自由空间的损耗,小尺度的衰落则主要是多径效应的影响。

2.1 自由空间传输损耗

在通信系统中,发射信号的幅度会随着传播距离的增加而减小,所以,当接收端的天线到发射端的天线距离越远时,接收端收到的信号能量就越小。这种因空间传播引起的信号衰减被称为自由空间传播损耗。自由空间的传播损耗可以表示为[19]

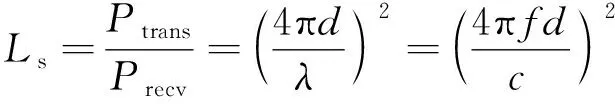
(8)

式中:d为两卫星天线之间的实际传输距离;Ptrans为发射天线的信号功率;Precv为接收端信号功率;λ为信号波长;f为信号频率;c为光速。一般在计算传播损耗时,采用对数值来表示,即

(9)

或者

(10)

从(8)式中不难看出自由空间的传播损耗与d和f直接相关,所以在实际应用中,只要确定了卫星间的距离d与卫星通信频率f,即可确定自由空间的损耗值。因此,可以将自由空间损耗在信道模型中看成一个乘性衰减,即将发射信号与自由空间损耗相乘便可得到经过该损耗之后的信号。

2.2 多普勒频偏

在星间通信中,由于收发端卫星间的相对运动及晶振偏差等,接收端收到的信号频率相对于发射端原信号频率将存在偏移,这种偏移即为多普勒频偏[20],其表达式为

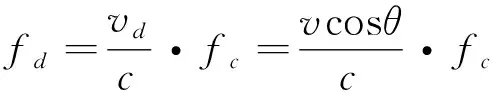
(11)

式中:fc为卫星通信载波频率;v为卫星之间的相对运动速度;θ为两卫星连线与v之间的夹角;c为光速。一般说来,若卫星的轨道已知,可利用STK软件对链路仿真获得多普勒频偏的范围。在卫星星座或编队中,同轨卫星间的相对距离较为固定,相对速度较小,多普勒变化范围较小,而异轨卫星间由于相对运动速度较大,多普勒频偏变化范围则较大。在信道模型中,可以添加一系数为ej2πfdt的乘性结构,使得信号频谱搬移fd以模拟多普勒频偏。

2.3 多径效应

在星座通信中,接收端的卫星天线相位中心处会收到多个不同路径传输过来的通信信号,实际的信号是由多路信号叠加而来[21],除卫星的直视路径外,还存在着间接反射到达的信号。

由于多径误差与通信卫星之间的瞬时距离、相对姿态、信号传播路径、天线几何形状等多种因素相关,而每个路径分量信号的时间延迟也不尽相同,属于小尺度衰落。具体来说,信号的多径传输是由信号的反射与绕射形成,其中信号的反射是信号遇到2个不同传输介质的分界面,部分信号仍在原介质中传播的现象,而绕射则是信号遇到比起其波长大得多的障碍物时发生的衍射现象。在卫星星座或编队中,通信两端卫星视距内并不存在地面建筑物类的大型障碍物,所以星座通信中信号的绕射现象基本可以忽略。因此,星座通信中的多径信号主要由卫星的星体、太阳翼板等物体反射产生。

对于反射信号的损失,一般用反射系数Γ衡量,定义为入射信号的场强幅度与反射信号的场强幅度之比,反射系数Γ与信号的入射角度、入射波极化、反射介质的相对介电常数等因素有关,其表达式为

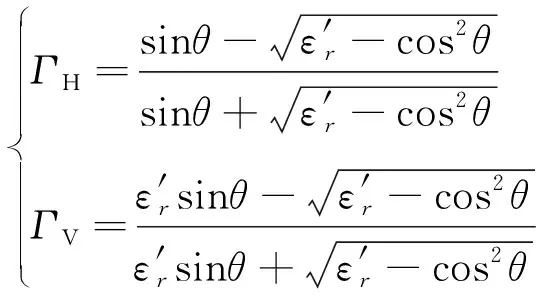
(12)

式中:di为多径信号空间传播路程长度;L为直射信号空间传播路程长度。

由于通信双方卫星一直处于相对运动状态中,因此信号的传输路径、传播时间也在不断变化中,故多径信号的自由空间衰减、反射角、时延亦为随机分布值,即在多径效应影响下,接收端收到的复合信号以直射信号为主,且存在其他随机分布的多径信号。根据统计学模型,可分析得接收端收到的复合信号r(t)符合莱斯分布特征,莱斯分布下r(t)表达式为

(14)

式中:K为莱斯因子,定义为直射信号的功率与多路信号功率之比;ac(t)与as(t)是2个独立的高斯随机过程。根据(13)式,多径信号相对于直射信号存在着更大的路径衰减与反射损耗,因此卫星的信号到达接收端时,多径信号相对于直射信号也比较弱,即在星座信道中,其莱斯因子K较大,接收端信号功率绝大部分为直射信号功率。

2.4 噪声

在实际的星间信道中,接收机的输入端信号会叠加许多噪声源产生的噪声,噪声源包括天线噪声、干扰噪声、接收机热噪声、量化噪声等。首先,由于天线本身材料损耗等会引入天线噪声,天线噪声与通信频率、天线仰角密切相关。其次,在现有的太空环境中,由于空间物质内部的分子热运动,物体会辐射各种频率的干扰电磁波,这种噪声在频段中均匀分布,近似于白噪声。最后,实际接收端由于内部射频链路中的低噪放、馈线等结构的存在,会产生接收机内部的热噪声,以及因为数模转化精度不足产生的量化噪声。

上述噪声源影响因素繁杂,很难提出逐一分析量化,但是这些噪声在频域范围内的分布大都比较均匀,即其统计模型为高斯白噪声。故在实际信道模型建立中,可通过添加一加性高斯白噪声(additive white Gaussian noise, AWGN)结构以模拟噪声效果。

2.5 信道模型建立

图6给出了经过上述分析后建立的星间链路信道模型。通道模型对信号的处理过程为:

图6 星间信道模型

1) 为了模拟自由空间传播损耗,信道模型使用乘法器将发射端信号乘以衰减α。

2) 为了对多径效应进行模拟,模型中采用2个相位正交的带限、零均值高斯随机过程相加形成复数域信号,以此建立莱斯分布模型来模拟多径传输信号,并与直射径信号叠加。同时,直射信号功率与多径信号功率之比为K:1。

3) 经过处理后的信号再次通过乘法器,乘法器系数为多普勒频偏量,以此机构模拟星间通信中的多普勒频移。

4) 给信号添加延时τ,借此模拟信号在空间传播所需时间。

5) 信号通过加法器添加一高斯白噪声以模拟星间中的噪声源,并且可通过噪声产生器灵活调节噪声大小。

3 仿真分析

为了对稀疏扩频通信系统在星间信道中的性能进行探究,利用MATLAB软件对该系统的核心算法进行实现,并依据图6所示的星间链路模型建立仿真信道,对稀疏扩频系统进行性能仿真。以某六星星座任务为代表进行建模,该星座卫星节点位置分布中,6颗卫星处于两低轨轨道中,每颗卫星既要与同轨的2颗卫星进行通信,也要在可见位置与异轨的3颗卫星进行通信。仿真平台设置的其他仿真参数如表1所示。

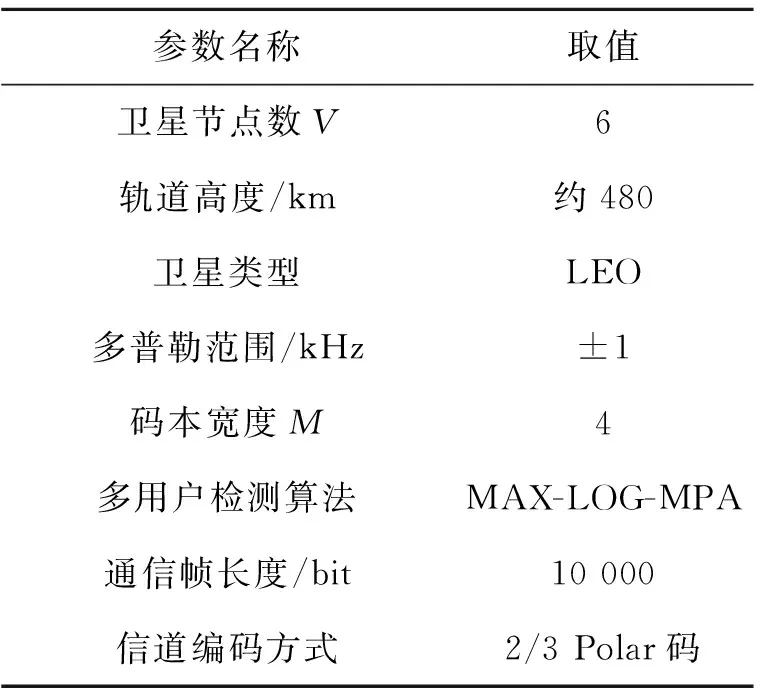
表1 系统参数

仿真设定中MPA译码算法使用较为成熟的MAX-LOG-MPA算法,表2给出了传统的MPA算法与MAX-LOG-MPA算法的运算复杂度对比。表中N为算法迭代次数,K为系统总体占用子载波数,dk为各子载波上叠加的用户数,M为码本宽度。从表中可得MAX-LOG-MPA算法通过将消息传递算法转换到对数域运算使得算法复杂度降低,使用该算法可以有效减少SCMA系统运算量,也更有利于SCMA系统的硬件设计和实现。

表2 算法复杂度对比

为了选择合适的过载因子与MPA译码算法迭代次数,对系统的通信性能与过载因子、MPA迭代次数关系进行仿真,仿真中使用误码率作为通信性能的衡量指标。同时,为了便于量化表示,采用能噪比Eb/N0作为衡量噪声与信号大小的指标,能噪比Eb/N0定义1 bit能量与噪声功率谱密度之比,在本文中,该指标与常用的信噪比RSN(signal noise ratio,SNR)转换关系可计算为

(15)

式中:M为码本宽度;V为卫星节点数;K为子载波数。

定义过载因子为用户数与所用子载波数之比,图7给出了不同过载因子下,系统的误码率与能噪比的关系曲线。仿真结果显示,相同能噪比下,随着过载因子的增加,通信误码率显著上升。图8为仿真所得误码率与MAX-LOG-MPA译码算法迭代次数的关系。从图中可以看出,在MAX-LOG-MPA译码算法中,迭代次数越高,算法收敛性能越好,最终误码率也越低,但当迭代次数超过5次后就会接近该算法的精度上限。根据表2可知,随着过载因子的增加,单个子载波上叠加的用户数增多,从而会使得算法复杂度呈指数性增长,并且随着迭代次数的增加,其算法复杂度也会线性增长。因此在稀疏扩频通信系统的算法具体实现中,综合考虑时频利用率、算法复杂度与通信性能,最终选取过载因子λ=150%、迭代次数N=5。

图7 稀疏扩频系统误码率与过载因子关系曲线

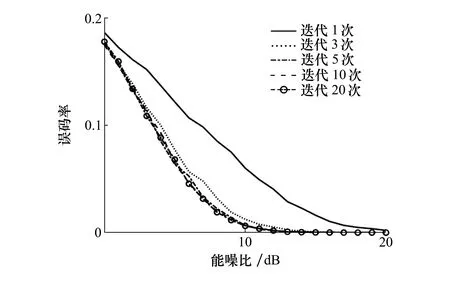
图8 稀疏扩频系统误码率与MPA迭代次数关系曲线

为了验证系统的核心SCMA算法在所建立的星间信道模型下的通信性能优化程度,将正交频分多址技术(orthogonal frequency division multiple access,OFDMA)和之前广泛用于星间通信的CDMA技术以及SCMA技术分别用于组网通信系统,并置于同一信道下进行仿真对比。CDMA使用典型的m码序列完成扩频映射,OFDMA使用6组完全正交的子载波,SCMA则使用4路正交子载波,并设置MPA算法迭代次数为5。图9给出了3种多址接入方式在该信道下的性能对比。从图中可得,3种多址接入方式的误码率随信号的能噪比增加而递减,即当接收端能噪比越大时,通信误码率越小。同时,在所设置的仿真平台下,SCMA取得了优于CDMA与OFDMA的误码率性能,并且在仿真中6颗卫星在使用OFDMA接入时使用了6组正交子载波,而使用SCMA接入时则只使用了4组正交子载波,因此在该系统实现时,SCMA技术有着优于OFDMA技术50%的时频资源利用率。

图10给出了当CDMA多址技术与本文建立的稀疏扩频多址系统分别用于点到点的通信时,2种通信算法在加性高斯白噪声(AWGN)信道、瑞利信道以及本文所建立的星座信道模型下的误码率性能对比,其中AWGN信道是常用的简化加性噪声信道模型,瑞利信道模型则是目前地面上的城市复杂传播环境常用的信道传输模型[22]。

一般说来,通常以误码率小于10-6作为正常通信的门限误码率,该误码率下的能噪比可称之为门限能噪比。根据仿真数据列出不同信道下的门限能噪比,如表3所示。根据图10及表3数据可见,在3种信道下,本文所建立的稀疏扩频系统相对于CDMA技术应用于点到点通信时,其门限能噪比均有着2 dB以上的优化。同时,稀疏扩频通信系统用于星间时,其误码率随着莱斯因子K的增加而减小,表明当莱斯因子越大时,直射信号相对于多径信号越强,此时通信性能也更好。

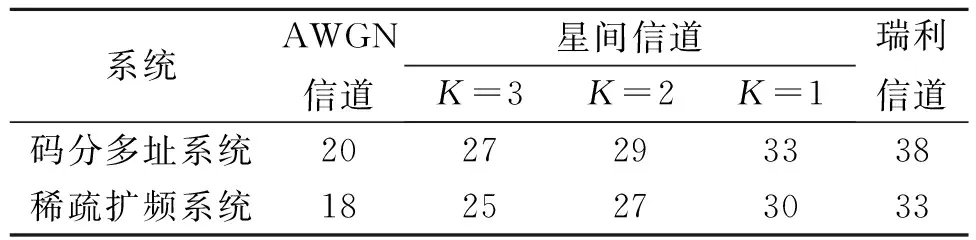
表3 不同信道下的门限信噪比 dB

4 结 论

本文针对大规模星座组网技术发展受时频资源紧缺制约的现状,以稀疏码多址接入技术(SCMA)为核心建立了一种适用于大规模星座组网的稀疏扩频通信系统,在系统具体实现时,提出了枚举遍历算法对稀疏码本进行设计,同时在系统通信数据帧中添加了适时引导序列并在接收端利用迭代矫正算法进行信道参数的估计。对大规模星座的星间信道各影响因素如自由空间损耗、多径效应、噪声、多普勒频偏进行深入分析并建立了对应星间信道模型,最终基于建立的星间信道模型对实现的稀疏扩频系统进行了性能仿真。仿真结果显示,在选取过载因子λ=150%且使用迭代次数N=5的MAX-LOG-MPA多用户译码算法情况下,以SCMA技术为核心的通信系统在提高OFDMA技术50%的子载波利用率的同时,在同等信噪比条件下取得了优于传统CDMA系统与OFDMA系统的误码率性能,且在多种信道下的测试表明,本文建立的稀疏扩频系统在点到点通信中,其通信门限能噪比要求相对于CDMA技术有着2 dB以上的明显优化。