岩石长时效变形损伤过程的分数阶模型研究
2023-09-11肖书文
肖书文
(山西泽州天泰锦辰煤业有限公司, 山西 晋城 048000)
1 前言
随着浅部煤矿资源开采殆尽,煤炭回采工作逐渐向深部迈进,深部巷道围岩长期处于高地应力的环境中会发生蠕变变形[1-3],合理的表征巷道围岩在长时间作用下的力学变形行为,量化变形规律,对于深部煤矿安全开采具有重要作用。
传统的岩石蠕变本构理论模型主要包含2大类,分别是经验模型、组合元件模型。其中经验模型主要根据实验数据进行多项式拟合,利用对数函数、指数函数、幂函数等相似函数进行组合,在形式上表征岩石应变与时间的关系,然而此种模型的参数意义不明确,普适性较低,不具备完整的理论力学基础[4-5]。组合元件模型,主要通过弹性体(胡克体)、黏弹性体(牛顿黏性体)、黏塑性体(圣维南体)进行组合,建立蠕变本构模型。此种模型的物理含义更为明确,具有完备的理论依据,在此基础上冯夏庭等采用Burgers模型建立了考虑体积蠕变的本构模型。徐卫亚等在黏性元件与塑性元件并联组合的模型上引入了蠕变系数,再通过与五元件模型进行串联,得到了可以反映第三蠕变阶段的七元件模型[6]。夏才初等构建了包含黏性、黏弹性、黏塑性、黏弹塑性的四元件蠕变模型[7]。
为更好的表征岩石蠕变行为,现有的蠕变模型往往采取增加元件的方式进行优化,然而过多的元件将会导致本构方程的参数增加,大大降低了工程意义。同时,深部岩体通常处于三维应力状态,传统的单轴状态下的蠕变本构方程难以充分考虑三维应力环境。因此,综合考虑上述问题,采用分数阶导数对蠕变元件模型进行改进,可以缩减本构方程的物理参数,同时构建三维的蠕变本构方程,并通过实验进行有效验证。
2 分数阶导数元件模型
2.1 分数阶导数定义
分数阶导数相比于整数阶导数的区别在于其导数阶次为分数,分数阶导数具有独立的数学定义方式,其中Riemann-Liouville微积分的定义方式最为广泛。设f在(0,+∞)上连续分布,并且在[0,+∞]的任何有限子区间可积,当t>0,Re(γ)>0时,称式(1)为函数f(t)的γ阶Riemann-Liouville分数阶积分。
(1)
式中,Γ(γ)为Gamma函数。
通过对式(1)进行逆运算,则得到Riemann-Liouville分数阶导数,如式(2)所示。
(2)
式中,m是大于γ的最小整数。
根据分数阶导数的定义,将传统的整数阶导数蠕变元件模型进行优化,可得到分数阶导数蠕变元件模型。
2.2 分数阶导数蠕变元件模型
牛顿黏壶在组合元件模型中用来表示黏性变形,其本构方程如式(3)所示。
(3)
式中,σ为应力,MPa;η为黏性系数;ε为应变,%;t为时间,h;γ为导数的阶次。
根据Riemann-Liouville分数阶微积分算子理论可将牛顿黏壶变换为以时间为自变量的应变方程。
(4)
在岩石长时效蠕变的过程中,岩石在恒定应力的作用下内部微观结构会逐渐发生损伤,随着微观损伤的逐渐积累,内部微裂隙会聚合扩展为宏观裂缝,使岩石进入具有强时效特征的第三蠕变阶段,并最终破坏。为表征岩石的损伤积累过程,考虑将损伤变量引入到岩石的力学参数中,用于表示岩石力学参数的弱化过程,引入的损伤变量如式(5)所示。
ηγ(D)=ηγ(1-D)
(5)
式中,D为损伤变量。考虑到损伤的积累是非线性的过程,因此,采用指数函数进行表示,如式(6)所示。
D=1-exp(-αt)
(6)
式中,α为损伤劣化系数。
将式(3)、(5)、(6)进行联立,最终得到考虑损伤过程的分数阶导数牛顿黏壶本构方程如式(7)所示。
(7)
3 分数阶导数蠕变本构模型
3.1 Nishihara蠕变本构模型
在岩石力学蠕变理论中,蠕变主要包含三个主要阶段,分别是第一蠕变阶段(初始蠕变阶段)、第二蠕变阶段(稳定蠕变阶段)、第三蠕变阶段(加速蠕变阶段),在蠕变过程中存在弹性变形、黏弹性变形、黏塑性变形以及损伤演化,可通过将元件模型进行组合得到相应的物理力学过程。日本学者提出的Nishihara蠕变模型被广泛用于描述第一蠕变阶段(初始蠕变阶段)、第二蠕变阶段(稳定蠕变阶段)。Nishihara蠕变模型如图1所示,主要包括弹性体、黏弹性体与黏塑性体,其总应变表达式为

图1 Nishihara蠕变模型
ε=εe+εve+εvp
(8)
式中,ε为总应变,%;εe弹性应变,%;εve为黏弹性应变,%;εvp为黏塑性应变,%。
3.2 分数阶蠕变本构方程
将Nishihara蠕变模型改进为分数阶Nishihara蠕变模型的方法是将模型中原有的牛顿黏壶替换为分数阶黏壶。
对图2所示的分数阶Nishihara蠕变模型的组合元件进行分析,推导其本构方程。对弹性体元件进行分析,其本构方程为
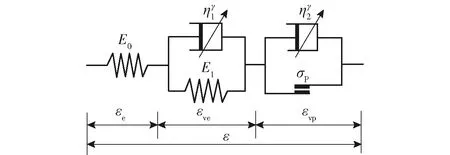
图2 分数阶Nishihara蠕变模型
(9)
式中,E0为弹性体的弹性模量,GPa。
对黏弹性体元件进行分析,其本构方程为
(10)
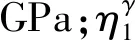
在分数阶导数理论中,为便于计算将Riemann-Liouville导数转化为Caputo导数,两种导数具有的数学关系为:
(11)
当t=0时,εve=0,利用Laplace双重变换得到黏弹性体分数阶本构方程。
(12)
对黏塑性体元件进行分析,黏塑性体中包含摩擦滑块,其主要物理意义在于表征应力阈值点,当应力大于阈值应力时,此元件启动,即代表当应力达到阈值应力时,岩石会发生具有长时效特征的第三蠕变阶段(加速蠕变阶段),摩擦滑块的公式为
(13)
式中,σp为摩擦滑块应力,MPa;σs为阈值应力,MPa。
考虑到蠕变第三阶段(加速蠕变阶段)的损伤演化趋势最为明显,因此,将损伤变量带入到黏塑性体元件中,经过Laplace双重变换得到黏塑性体的本构方程。
(14)

将上述弹性体元件、黏弹性体元件、黏塑性体元件进行叠加,得到分数阶蠕变本构方程方程。
(15)
为简化表示式(15),在式中引入双参数Mittag-Leffler函数(式(16)),将式(15)变换为式(17)。
(16)
式中,α、β为函数参数;z为函数自变量;k为函数阶次。
(17)
4 三维分数阶蠕变本构模型
深部岩石通常处于三维应力环境下,因此,忽略围压的本构方程往往不能有效地表征深部岩石地力学行为,三维应力环境下,蠕变的总应变为
(18)
根据广义胡克定律,将蠕变变形分解为偏应变与球应变,偏应变状态下的弹性体三维本构方程为
(19)
式中,eij为应变偏张量,%;sij为应力偏张量,MPa;G0为弹性体的剪切模量,GPa。
相应的,可得到偏应变状态下的黏弹性体三维本构方程为
(20)
式中,G1为黏弹性体的剪切模量,GPa。
黏塑性体中包含塑性变形部分,因此,在建立三维状态时,需要引入屈服函数,采用关联流动法则,黏塑性体三维本构方程为:

(21)
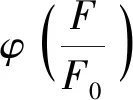
(22)
(23)
式中,F为屈服函数;F0为屈服函数参考值,取1;φ为幂函数,取1;J2为应力偏量第二不变量。
假设两向围压σ2=σ3,则得到以下条件:
(24)
将式(19)~(24)联立,最终得到偏应变状态下的三维分数阶蠕变本构方程:
(25)
同理,按照相同方式,可得到球应力状态下的三维分数阶蠕变本构方程:
(26)

将式(25)与式(26)合并最终可得到三维全应力状态下的分数阶蠕变本构模型如式(27)所示:
(27)
式中,δij为狄利克雷函数。
5 岩石蠕变实验验证
5.1 岩石蠕变实验方案
为验证本文推导的三维分数阶本构方程,采用晋城市锦辰煤业3采区巷道砂岩进行常规三轴加载实验。实验采用Rock Triaxial V4三轴流变仪如图3所示。

图3 三轴流变仪
实验根据砂岩的赋存状态,同步加载围压与轴压,加载速度为2.0 MPa/min,当加载到20 MPa时,保持围压不变,继续加载轴压直至达到30 MPa,随后保持三向应力恒定,直至砂岩破坏。
5.2 岩石蠕变曲线拟合
蠕变实验共选取3个砂岩试样开展,将实验曲线与三维分数阶本构模型进行拟合,得到图4所示的拟合曲线。根据图中所示,砂岩的蠕变曲线表现出明显的三阶段蠕变变形。对比结果显示,推导的本构模型可以很好的描述深部砂岩的三轴蠕变实验数据,拟合参数见表1。

表1 拟合参数表

图4 三维分数阶本构模型与实验数据拟合曲线
6 结论
(1)根据分数阶导数理论,将牛顿黏壶改进为分数阶黏壶,考虑到岩石内部的损伤演化,引入指数形式的损伤变量描述蠕变的第三阶段。通过改进Nishihara蠕变本构模型建立分数阶Nishihara蠕变本构模型。
(2)考虑到深部岩石的三维应力状态,根据广义胡克定律,将分数阶Nishihara蠕变本构模型分解为偏应力三维分数阶蠕变本构方程与球应力三维分数阶蠕变本构方程,最终建立全应力状态下的三维分数阶蠕变本构方程。
(3)采用晋城市锦辰煤业3采区巷道砂岩进行常规三轴加载实验,实验数据具有明显的蠕变三阶段变形特征。推导的本构模型可以很好的描述深部砂岩的三轴蠕变实验数据,验证了模型的可靠性。
