基于复杂移动热源模拟的激光自熔覆试验研究

雷晓星,曹志勇,张悦,徐承亮

(1广州科技贸易职业学院现代教育技术中心, 广东 广州 511442;2.湖北大学材料科学与工程学院, 湖北 武汉 430062)

0 引言

随着工业4.0时代的发展,各类零件的生产要求及标准不断提高,在保证质量和精度的情况下,覆盖件模具型腔的加工工况也愈加复杂.生产中,磨擦、冲击等复杂应力的共同作用于模具表面,极易致使模具发生磨损、变形等损坏,甚至导致表面失效.为了解决模具在生产过程中过早失效而导致的成本增加、制造工期延长、产品质量差等难题,提高覆盖件模具的产品质量和使用寿命、优化模具表面强化技术工艺是一个重大的挑战.激光自熔覆技术是一种利用高能量密度激光来改善金属综合机械性能的表面强化工艺技术[1],在生产实际中,由于激光自熔覆瞬时热输出非常高,当材料成分、扫描工艺及参数等条件不同时,工件经过激光扫描后将产生组织、尺寸、形状等变化.工艺不合适或相变硬化表面积较大,可能引起较大变形,从而影响产品质量.工艺参数和材料属性都会影响自熔覆后的工件质量,这些因素耦合在一起,使得激光自熔覆后工件的形变和硬度是否能达到预期值特别突出,为了自熔覆后能达到预期的强化硬度,将加工后的工件形变量控制在一定范围内,通常会使用试错法或冗余法,但单纯使用正交实验,会消耗大量时间成本和人力成本[2].

采用有限元数值模拟来预测激光自熔覆对工件的影响,使用计算机建立模型预测激光强化后的硬度及形变程度,可在一定程度上减少材料自熔覆加工过程中的试错成本,可以有效避免上述提到的在线测量困难、成本高等一系列问题[3-4].有限元模拟是预估激光加工实验过程的一种很好的方法,Zhang[5]等通过分析不同的激光加工方式之间的机理差异,提出了一种含有几何、物理方面的模拟仿真,可适用于所有激光加工方式.Sidi-Ahmed[6]等结合数值模拟和实验,建立了激光硬化3MA-涡流模块的有限元模型,有限元模拟的结果证实,所获得的信号与试样材料的磁性具有内在联系.根据涡流信号与激光硬化深度的关系曲线,可以在指定频率下准确评估趋肤深度.Alisin[7]等建立了NiCrBSi工件表面添加氧化铝细粉硬化的激光熔融强化过程的有限元模型.获得了微分方程组的数值解,研究了热源的功率和作用时间与涂层的温度分布之间的关系.

但是,目前关于激光自熔覆有限元模拟,主要研究的是二维平面模型或者可以使用公式表达自熔覆轨迹的三维模型.此类方法可以用于简单的规则工件或者不需要考虑细节的工件.对于具有表面有凹槽、凸起的工件,其自熔覆轨迹大多数是无法用公式表达的,现有的热源程序已经不能满足需求.针对这种情况,本研究在原有的热源程序基础上提出了线性插值算法,改进后的热源程序可适用于各种复杂的熔覆轨迹.本实验中仅需要使用相对少量的实验数据用于修改和验证有限元模型,就可以得到准确率较高的预测模型,使用该模型能预测所有参数组合的工件质量情况,可以为之后有关该材料的工件提供实验参考并减少工件试验成本.

1 热源模型的确定

1.1 高斯热源通用模型通过大量的实验可以得知,在较为宏观的温度分布及温度梯度研究当中,热量对系统的宏观加载作用过程可通过热源模型来很好地描述[8],高斯热源模型是一种典型的热源模型,用来描述激光能量在平面上的分布规律,该热源模型分布函数经常用于激光加工中.

高斯热源模型为:

q(r)-q(m)exp(-kr2)

(1)

其中,q(r)表示坐标为(x,y)点的能量,q(m)表示激光光斑中心的能量,k为高斯光源能量集中系数,通过能量守恒定理和积分,可得高斯热源的解析公式:

(2)

其中,q(x,y)为坐标为(x,y)的能量值,η为激光吸收效率,r1、r2为坐标轴x,y对应的热源半径.

1.2 本文中提出的热源模型激光自熔覆与其他激光强化技术不同,仅作用于材料表面,所以更合适使用平面热源模型.高斯热源模型的中心光强极高,四周光强弱,采用这类光束模式实际上不利于激光自熔覆后材料组织和硬度的均匀性,通常要选择光强分布均匀的激光光束.考虑到使用矩形热源时,热源中心的温度与热源四周的温度相差不大.所以本文根据均匀分布的平面热源模型[9],推导出单位矩形光斑面积内的某一点的激光功率分布函数,即平面移动热源公式,并应用到有限元模拟中,如下所示.

F=η*P/(L*W)

(3)

其中,F为热通量,η为激光器功率效率,P为总功率,L为矩形光斑的长度,W为矩形光斑的宽度.

2 有限元模型的材料参数

本数值模拟实验中,使用的有限元软件为Abaqus,具体步骤如下[10].

2.1 建模及网格划分激光自熔覆实验中的有限元模型如图1(a)所示,考虑到工件的对称性,仅用一半的模型进行分析,结点总数:23 892,单元总数:47 784 ,单元定义为 C3D6T 温度-位移耦合单元.

2.2 材料参数设定有限元模拟中的材料参数设置依据为德国标准(德标)GGG70L材料的化学成分,如表1所示,表2中的材料参数由专业材料性能模拟软件(JMatPro)根据表1计算获得.

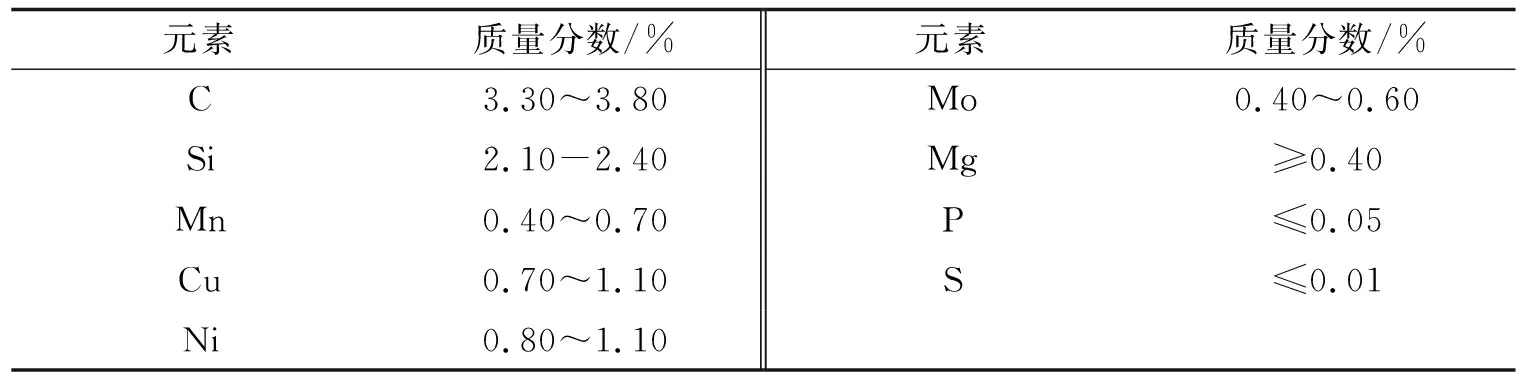
表1 德标GGG70L材料化学成分

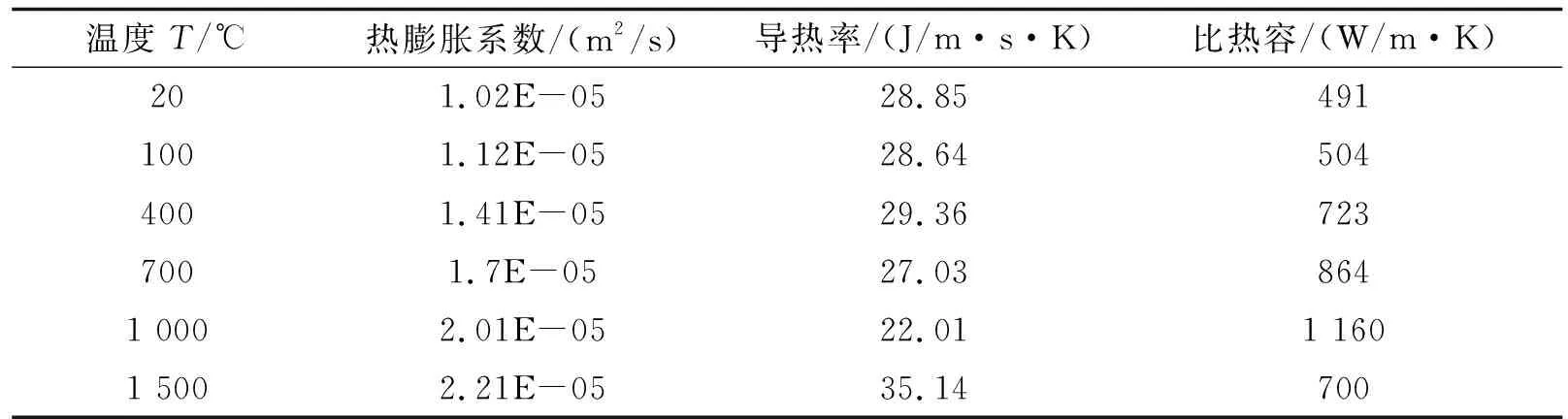
表2 德标GGG70L材料参数设置

2.3 复杂三维移动热源程序开发Abaqus软件允许用户使用Fortran语言编写热源程序.大多数文章中分析的移动热源轨迹仅涉及简单的二维空间,仅由宽度→水平线和高度→垂直线构成,在几何学中即为X轴和Y轴两个要素所组成的平面空间.如在长方体模型,激光热源在某个二维平面沿直线或者圆形路径做功,且路径可以由简单的二维函数表达出来.但是在工程实验中,工件表面的激光自熔覆往往涉及更为复杂的三维路径.

复杂的三维路径所产生的三维坐标点(x,y,z)不能由简单的函数表达出来,使用拟合工具所得到的函数与实际路径有较大的误差,需要采取其他的方法来获取工件表面的复杂三维轨迹点[11].本文中提出线性插值的方法来实现三维复杂热源移动轨迹程序,具体步骤如下:

1)获取三维模型的轨迹点.

本研究采用SprutCAM软件导入模型获取工件的三维路径轨迹点,SprutCAM是一款俄罗斯的机器人离线仿真与编程软件,导入模型后,选择加工路径及轨迹点的疏密度,导出获得的机器人文件中就包含该三维路径的所有轨迹点,如图1(b)所示.

2)正则化轨迹点文件.

导出获得的机器人轨迹文件除了轨迹点,也包含了大量机器人的设计参数,可以通过Python或其他工具正则化处理得到只含有三维坐标点的文件.

3)Fortran程序编写.

线性插值是指插值函数为一次多项式的插值方式,其在插值节点上的插值误差很小,可以用来近似代替原函数.

核心程序如下:

XXT=xx(i)-xx(i+1)

(4)

YYT=yy(i)-yy(i+1)

(5)

ZZT=zz(i)-zz(i+1)

(6)

dd(i)=SQRT((YYT*YYT)+(XXT*XXT)+(ZZT*ZZT))

(7)

(xx(i),yy(i),zz(i)),(xx(i+1),yy(i+1),zz(i+1))为相邻轨迹点,dd(i)为两个轨迹点的距离,通过循环操作,可以得到所有轨迹点间的距离.

ratio=(a-d1)/(d2-d1)

(8)

X_center=xx(n1)+ratio*(xx(n2)-xx(n1))

(9)

Y_center=yy(n1)+ratio*(yy(n2)-yy(n1))

(10)

Z_center=zz(n1)+ratio*(zz(n2)-zz(n1))

(11)

式(8)中,a为某时刻移动热源轨迹的路径长度,(X_center,Y_center,Z_center)为该时刻热源中心点,ration为该时刻移动热源中心在两个轨迹点中的插值比例,由式(9)～(11)得到该时刻热源中心点的坐标.

2.4 有限元模拟方案有限元模拟时,加载时间为20 s,激光功率效率选择为0.3,功率为 1 800 W,矩形光斑长为0.01 m,宽为0.005 m.图2为上述条件下,工件分别在4.019 s (a)、8.047 s (b)、11.01 s (c)、16 s(d) 时的温度场分布情况,耦合线性位移量和组织晶粒度分布情况,可以估算出最大和平均的形变量以及硬度值,本实验取的平均值.

图2 工件在4.019 s (a)、8.047 s (b)、11.01 s (c)、16 s (d)时的温度分布情况

从图2中,可以看出激光矩形光斑在不同时刻沿三维模型的凹槽处熔覆时的温度场变化,说明使用基于线性插值的复杂三维热源移动轨迹程序可以很好地模拟复杂的轨迹.分析温度分布可知,在激光辐射表面的瞬间,光斑中心温度可达到1 300 ℃,且热量集中在矩形热源处,光斑热源周围的温度比激光辐射区低,这说明激光能量密度较高,这也是激光表面改性技术为什么适于高精度的零件处理.图中可以看出熔覆区温度下降速度很快,不久就接近室温.极快的加热冷却速度对工件热影响小,工件的形变量也就小,一定程度上保证了工件在加热后提升硬度的同时工件形变量较小.

3 有限元模拟分析

3.1 激光参数对形变量的影响本文中使用有限元模拟来分析不同工艺参数,即不同激光功率和扫描速度对形变量的影响,从而可以验证有限元模拟与实验值的误差在可接受范围内.

3.1.1 激光功率的影响 设计了4组实验,每组5个实验,共20个实验.具体工艺参数为光斑大小:13 mm,激光移动速度为4、6、8、10 mm/s,激光功率在800～2 000 W之间变化,形变量模拟结果如图3所示,由图可知,在相同的光斑大小和激光扫描速率下,工件熔覆后的形变量,随着激光功率的增加而增加.激光功率越大,作用在工件的温度越高,熔覆后的形变量也就越大.

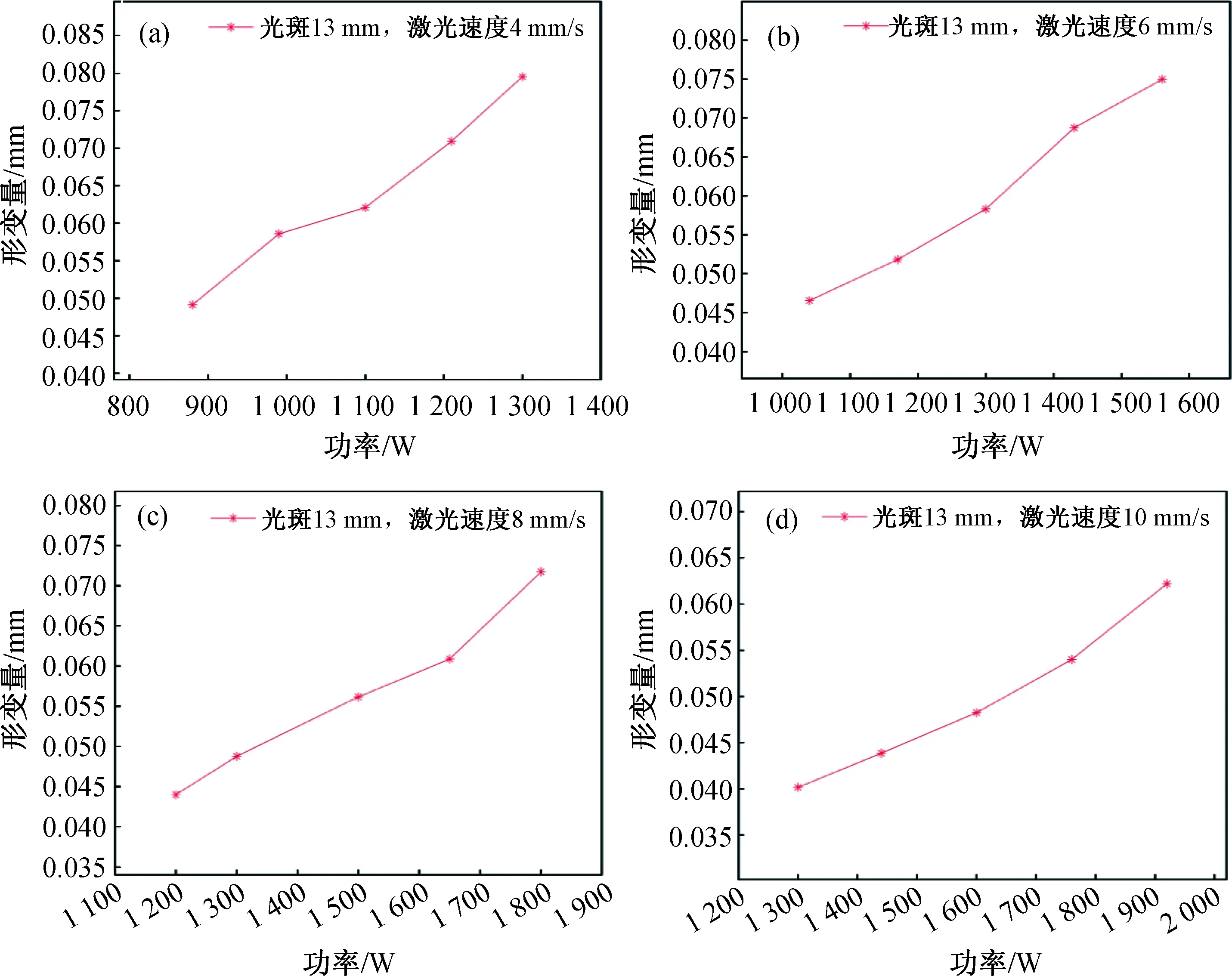
图3 激光功率对熔覆后形变量的影响

3.1.2 激光扫描速度的影响 设计了2组实验,每组4个实验,共8个实验,激光功率分别为1 300 W和2 300 W,光斑大小分别为13 mm和20 mm,激光移动速度在4～10 mm/s之间变化.不同工艺参数下形变量结果如图4所示,由图可知,在相同的光斑大小和激光功率下,工件熔覆后的形变量,随着激光扫描速率的增加而减小.因为激光扫描的速率越快,激光在相同的熔覆部分停留的时间越短,所以热量的积累越小,导致形变量越小.

图4 激光扫描速度对熔覆后形变量的影响

3.2 激光参数对硬度的影响

3.2.1 激光功率的影响 设计了4组实验,每组5个实验,共20个实验,光斑大小为20 mm,激光移动速度分别为4、6、8、10 mm/s,计算的工件表面硬度结果如图5所示,由实验结果可知,在相同的激光光斑大小和扫描速度的条件下,工件的表面硬度(HV,维氏硬度),在640～780 HV之间变化,工件表面硬度先随着激光功率的增加而增加,达到一定峰值后,随着激光功率的增加而减少.原因如下:当激光功率过大,加载在试样上的温度过高,会使工件表面熔凝严重,内部出现有发黑的氧化物,使表面硬度反而不高.

图5 激光功率对熔覆后表面硬度的影响

3.2.2 激光扫描速度的影响 设计了2组实验,每组4个实验,共8个实验,激光速度在4～10 mm/s之间,光斑大小分别为13 mm和20 mm,激光功率分别为1 300 W和2 000 W.计算的硬度结果如图6所示,由实验结果和图6可知,在激光输出功率和光斑大小不变的情况下,熔覆后工件的硬度随激光扫描速度的增大而减少.造成这种现象的原因是:当激光输出功率和光斑大小不变时,扫描速度越小,则激光束作用在表面材料上的时间越长,材料吸收的激光束能量越多,相反,扫描速度越大,材料吸收的激光能量越少,从而使得奥氏体的晶粒越难长大,在之后的冷却过程时,所得到的马氏体组织也比较均匀细小,使工件的熔覆层硬度下降.

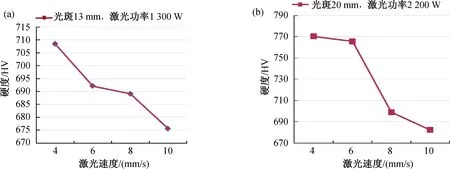
图6 激光扫描速度对熔覆后硬度的影响

4 工程实验研究

4.1 实验准备实验采用的是德标GGG70L模具材料,在激光熔覆前,要对样品进行预处理,首先将基体材料用砂纸磨平,去除表面氧化层,并用丙酮和酒精洗去油污后待用,试验采用RFL-C6000激光加工平台,最大输出功率为6 000 W,运动装置为KUKA-KR60型六自由度机器人平台,如图7所示.

将加工好的工件置于激光加工台上,调整机床的工作位置,设置离焦量和光斑尺寸后,对机器人进行加工编程从而控制激光扫描路线,激光熔覆加工过程如图8(a)所示,图中工件红色部位为入射的激光,激光熔覆加工后的工件及其表面如图8(b)所示,激光熔覆加工后的工件会进行形变量和表面硬度的测量,以获取不同激光参数下的形变量和表面硬度的数据.

图7 激光加工机器人平台

图8 (a) 激光熔覆加工过程中(工件红色部位为入射的激光);(b) 激光加工后的工件及其表面

4.2 激光加工后性能验证

4.2.1 形变量测试 激光熔覆加工实验的工艺参数为:激光光斑20 mm,激光扫描速率8 mm/s,激光功率3 000 W.为了测试激光熔覆前后工件的形变,测量形变量采用的三坐标测量仪为 Global 575系列型号,如图9(a) 所示,测量工件表面样点的探头如图9(b)所示,对其熔覆前后的外表面轮廓进行取点扫描,以测量轮廓变化,测量取工件的16个样点,如图9 (c)和 (d)所示.

图9 三坐标测量仪测试形变量及其方法

4.2.2 硬度测试 激光自熔覆后将试样沿垂直于自熔覆轨迹的方向线切割开,对其横断面进行打磨(砂纸从200～2 000目)、抛光.按照GB/T 4340.1标准,采用9.8 N负荷的维氏硬度计进行硬度测量.在试样同一横截面上取5个点进行硬度检测,最后取其平均值.沿自熔覆轨迹方向间隔适当距离选取5个不同横截面位置,每个横截面位置取4个点,获得包含20个点的阵列,对点阵位置的硬度进行检测,以硬度的标准差作为硬度均匀性参数.使用4%硝酸酒精溶液作为侵蚀剂显示试样的显微组织,采用显微组织测量法测量自熔覆后试样的淬硬层深度.在试样的横截面上,从表面垂直测至热影响区顶端的距离为淬硬层的深度.

4.2.3 形变量实验和有限元对比 使用Abaqus构建与实验相同的模型,自定义移动热源代码设置和实验相同的工艺参数,采用激光光斑20 mm,激光扫描速率8 mm/s,激光功率2 800 W.在Abaqus中创建显示组,选取和测量形变量时相同位置的16个测量点.将模拟结果与实验结果进行对比分析.经过几次对比修改后,最终有限元模拟结果与实验值的误差如图10中可以看出,实验和模拟结果误差较小,说明模型是可靠的.误差范围在之内.说明模拟数据比较可靠,可一定程度上代替实验,进行分析.

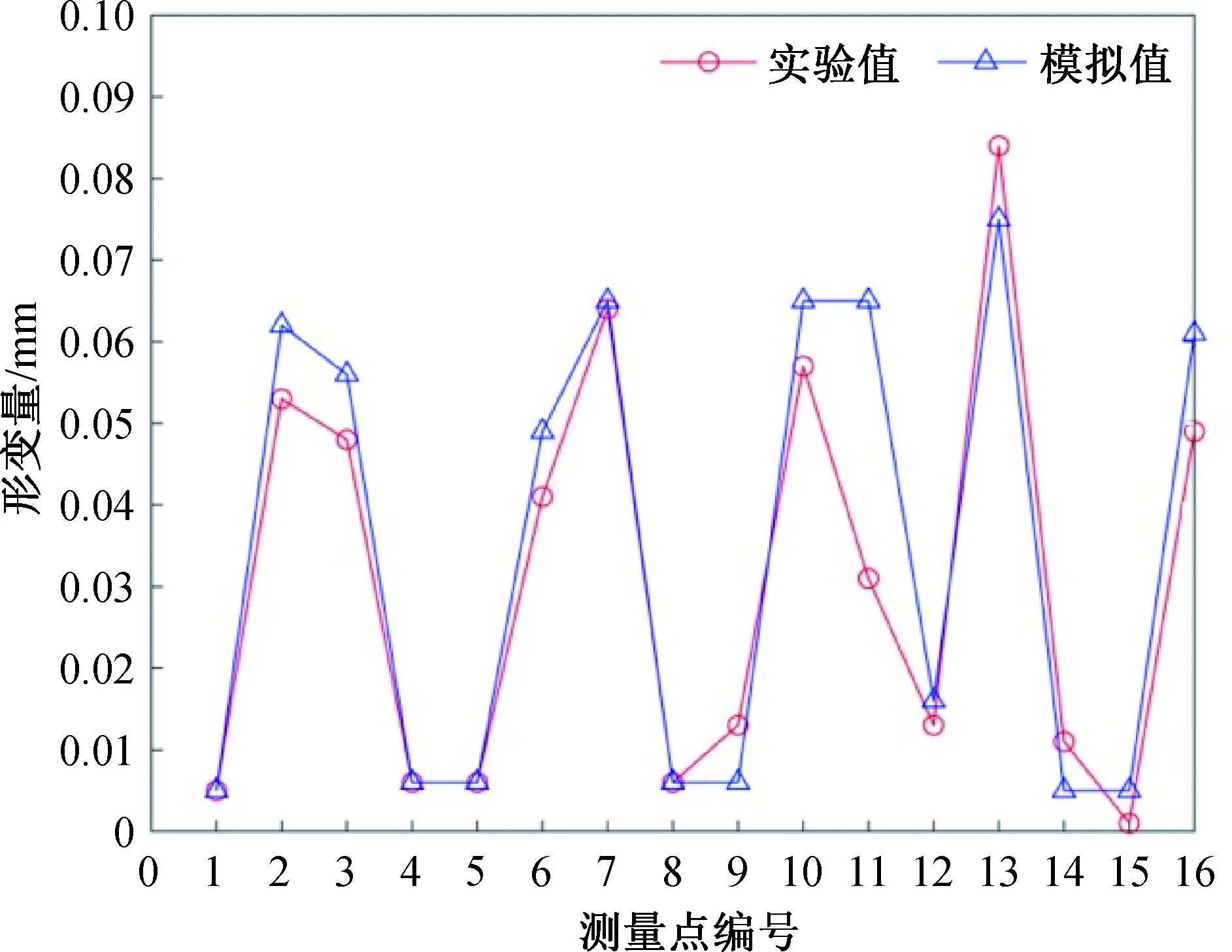
图10 形变量的模拟和实验结果对比

5 结论

1)本研究利用激光自熔覆有限元模拟技术,采用线性插值法改进热源程序,建立准确性较高的预测模型,实现了复杂三维热源移动轨迹,解决了在工程实验中激光自熔覆所涉及的更为复杂的三维路径问题,可适用于各种复杂的熔覆轨迹;

2)通过新建的有限元模拟模型,利用Abaqus软件对不同的工艺参数进行模拟,得出的模拟数据在工程实验中进行分析,说明模拟模型精确度比较高,模拟数据是可靠的,一定程度上可代替工程实验进行分析,减少试验中浪费的大量人力、物力和财力成本.