发动机试验动态数据处理方法综述

刘子星 ,高 俊 ,宋炯亮 ,林 萌 ,杨 懿

(1.北京动力机械研究所,北京10074;2.北京航天试验技术研究所,北京 100074)

1 引言

发动机试验是解决发动机研制过程所遇到的问题、推动理论研究和完善发展发动机设计理论的基本途径,也是分析发动机技术参数和评估发动机性能和评判发动机能否定型的重要方法[1]。在发动机试验中,各种测量数据是研究发动机性能、定位各类型故障、计算可靠性等的重要依据。

数据处理是将反映物体状态的物理量随时间变化的原始信号转换成某些适合于工程设计、试验和分析的简化量。数据处理贯穿于发动机设计、试验和生产的各个阶段,其目的是揭示动力学环境、制定试验条件、设计准则以及诊断故障和提供信息[2]。

对发动机试车的动态参数进行分析是研究发动机各项性能指标的重要依据。例如,分析推进剂的流量数据能够精确计算发动机比冲和混合比。分析推力和稳态压力能够研究发动机实际工作性能以及发动机与试车台之间的协调性。推力室脉动压力是研究发动机启动特性与不稳定燃烧、管路特性和定位发动机故障原因的重要依据。振动参数是研究推力室、燃气发生器、涡轮泵等关键部件结构性能、不稳定燃烧状态等非常重要的参考依据。因此,研究动态数据的分析和处理方法,不仅关系到发动机零部件的性能评价,也是准确评估发动机总体性能、发动机和试车台匹配程度等的重要依据。

目前,随着数字信号分析技术的发展,业内研究人员对动态数据分析已经由最初单一的傅里叶变换分析发展到小波分析、小波包分析、Hilbert-Huang 变换、人工神经网以及多种分析方法相结合的灵活运用和推广[3,4]。在本文中,总结了上述多种方法的理论特征,梳理了该方法在动态数据分析领域的应用情况,为深度挖掘试验数据信息、提高发动机性能和提高发动机设计能力提供了参考依据。

2 发动机试验动态数据处理方法

2.1 FFT 方法

快速傅里叶变换(FFT,1965)的基本思路是将时域采样点数分解为组合因子,按照组合因子将整个数据序列分割为若干子序列。先计算各子序列的离散傅里叶变换,然后将子序列变换结果加以合成,从而得到整个序列的离散傅里叶变换[2]。该方法的局限性在于缺乏分析时域内局部频率数据的能力。

在工程应用中,采用计算机对时域连续傅里叶变换进行离散化时会不可避免地产生一些问题:

(1)时域离散化引起频域的周期延拓,很可能产生频率混淆;

(2)时域的截断引起泄漏;

(3)频域的离散化引起时域的周期延拓。

为解决上述问题,诸多研究人员制定了相应的解决办法,如加入抗混滤波器、窗函数、提高采样率等[2]。

目前,FFT 方法已经广泛应用于航空、航天发动机试验振动数据和脉动压力数据等的分析处理中[5-8]。

胡海峰等根据R 语言在统计分析方面的优势,在VC 软件平台结合R 语言的编程实现发动机数据分析处理。采用FFT 方法分析点火启动及拖尾段的含噪波动数据,根据时域内振动信号的频谱图,识别信号高低频的有用信息[9]。

孙百红等系统归纳了FFT 方法对液体火箭发动机试验振动数据进行分析的步骤和路线。采用FFT 分析方法对某型号液体火箭发动机试验出现故障的稳定段振动数据进行频谱分析,通过对比正常数据的幅频特性,成功定位某试验件结构破损的故障。通过对振动数据RMS(Root-Mean-Square,均方根)特性分析,绘制振动数据特征频段全程瀑布图,能够有效识别试车中的故障[10]。

牛伟等将航空发动机转速高齿信号作为分析发动机振动状态的基础,提出了基于FPGA 的振动信号采样设计流程:采样-滤波抽样-三次样条插值-信号抽取-傅里叶变换,制定了振动数据频域特征提取处理流程。通过对试验数据进行分析,证明该方法不仅运算简单、分析精度高、实时性强,而且有效解决了FFT 方法分析过程中的频谱泄露和栅栏效应等问题[11]。

杨懿等针对液体火箭发动机脉动压力数据采样率高和系统响应频率快的特点,采用FFT 方法对脉动压力数据进行分析。根据脉动压力数据的频谱特性,结合推力室轴、径向和切向三个振动测点的数据,有效定位发动机不稳定燃烧的声振类型[12]。

陈子豪等为了验证固体火箭发动机试车过程中因不稳定燃烧所产生的压强异常升高和发动机推力值异常振荡的问题,采用FFT 方法分析推力室压强的幅频特性和燃烧器的试验数据,得到压强振荡的倍频关系,结合声学仿真的结果,证明该方法能够有效分析发动机不稳定燃烧的机理[13]。

洪亮等采用FFT 方法,通过统计分析转子在不同转速下的倍频特征和振动量级之间的关系以及转子临界试验中的幅频特性,得出了转子发生故障的特征和原因,为优化和提高发动机设计提供了重要的参考依据[14]。

钟永恒等针对航空发动机外部管路流固耦合振动是导致发动机外部管路故障的重要因素之一,根据所推导的直管管路流固耦合偏微分方程建立管路系统物理模型,采用C++语言开发了仿真分析软件,研究MOC-FFT 方法分析计算外部管路时频响应特性和固有频率。通过动态压力特性试验,验证了该模型的有效性和准确性[15]。

发动机试车过程中,不同系统之间往往存在关联,因此,通常将不同测点的脉动压力数据、振动数据等结合起来进行分析,便于分析发动机的性能和故障定位。

以某型号发动机试验为例,将振动测点数据和推力室脉动压力数据[12]的分析相结合。脉动数据采样率为10 kHz,稳定段0.02 s 的数据如图1 所示。

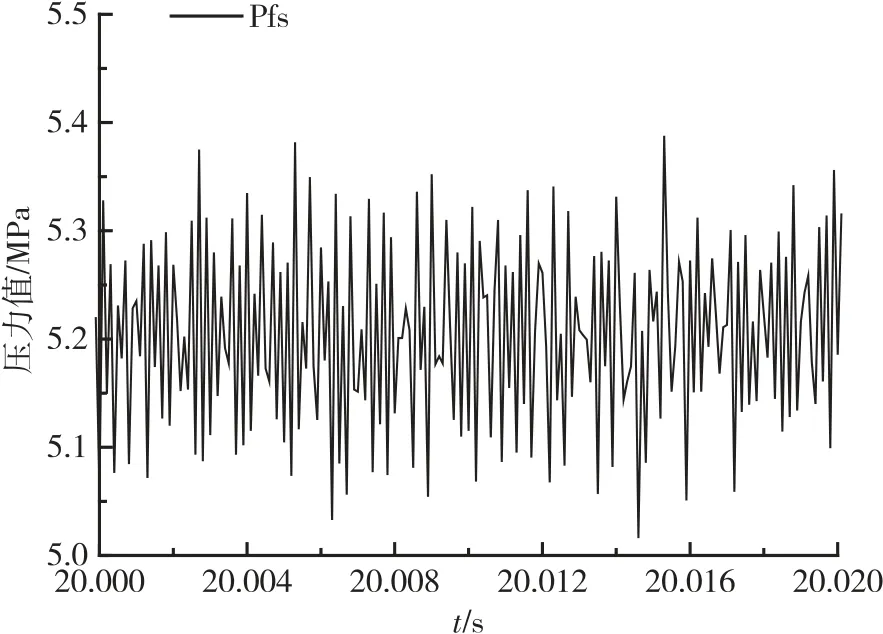
图1 推力室脉动压力数据图Fig.1 Fluctuating pressure data diagram of thrust chamber

采用FFT 方法对脉动压力数据进行频谱分析,0～11 000 Hz 频率段的频率-幅值特性曲线如图2所示。

图2 推力室脉动压力数据FFT 频谱图Fig.2 FFT spectrum of fluctuating pressure data

分析图2 的幅频曲线,推力室脉动压力的幅值峰值主要集中在0～5 500 Hz 的频率段内,5 500～10 000 Hz的高频段幅值曲线较为平坦。在中、低频段,500～3 500 Hz 幅值存在多个小幅度波动,可能与发动机工作倍频有关系。5 000 Hz 左右存在一个高峰值波峰,可能与发动机中频共振和不稳定燃烧有关。对于脉动压力数据频谱分析需要结合发动机振动数据进一步分析。采用FFT 方法对推力室轴向、径向和切向三个振动测点数据进行分析,其中径向测点ab1-2 的频谱分析结果如图3 所示。

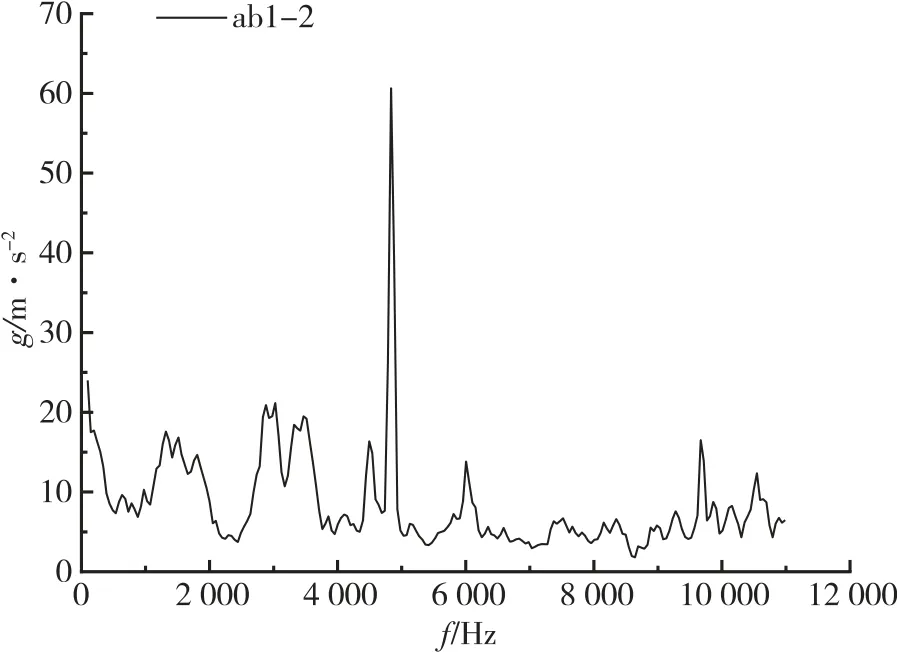
图3 推力室径向振动测点FFT 频谱图Fig.3 FFT spectrum of radial vibration measuring point

从图3 可知,径向振动测点在1 000～5 000 Hz低频率段中存在多个幅值峰值,5 000 Hz 左右也存在一个高峰值波峰,说明脉动压力数据与径向振动测点存在关联。对脉动压力、推力室轴向、径向和切向振动测点数据FFT 频谱分析结果如表1 所示。

表1 推力室振动测点与脉动压力幅频数据表Tab.1 Data of vibration measuring points and fluctuating pressure amplitude frequency of thrust chamber

从表1 可知,在1 611 Hz、2 884 Hz、4 822 Hz 和9 643 Hz 时,振动径向测点的幅频峰值特性与脉动压力测点的幅频峰值特性存在耦合关系。轴向和切向振动测点与脉动压力耦合点较少,由此可以推断推力室发生高频横向声振。

从上述分析过程可知,采用FFT 分析方法,结合脉动压力、振动等多类型的动态数据能够为判断发动机不稳定燃烧状态和评价发动机性能提供有力的参考依据。

2.2 小波分析方法

小波分析方法以傅里叶变换为基础,具有良好的自适应优势。比利时数学家Ingrid Daubechies 系统总结了上世纪80 年代以来诸多研究人员以及自己对小波的先进研究成果,编写了文献[16],对小波分析的基本理论、性质、适用领域和使用规则进行了详细介绍,使得小波分析成为一门真正的应用学科,并成为国际研究热点。小波分析在发动机动态数据处理中的应用主要集中在数据去噪、奇异点检测分析等方面。

符娆等针对航空发动机转、静子发生碰摩时,振动信号频率产生急剧变化的特点,利用小波分析在局部信息中具有高分辨率的优势,采用阈值法先对原始含噪振动信号进行去噪处理,再提取有价值信号中的幅值特征和能量信息。通过对试验数据分析表明,降噪效果较好,能够准确跟踪信号中的突变信息[17]。

文壁等重点分析了涡扇发动机起动过程中转子做功脉动压力、噪声脉动压力、失速团引起的脉动压力和燃烧波动引起的脉动压力四种成分,利用小波分析在时频分析领域的优势,对含噪信号进行分解,对多次起动过程的频谱图,结合起动过程的压力脉动现象进行分析,结果显示小波分析方法能够清晰识别压力测点不同转速下的脉动频率,定位脉动压力异常的原因[18]。

耿纪洲等运用小波分析和分形算法相结合的方法对发动机轴承磨损的含噪数据进行去噪处理,分析结果显示该方法能够清晰提取轴承的故障特征以及判断最佳的故障诊断部位[19]。

肖云魁等针对小波分析理论中Lipschitz 指数不能清晰定位汽车发动机曲轴轴承工作异常过程中的奇异点和对奇异点能量大小的描述不够精确的问题,先对试验数据进行去噪,再采用模极大值多尺度分析方法,对轴承故障数据进行分析。仿真和试验验证的结果显示,该方法能够精确定位试验过程中的奇异点位置[20]。

戴屹梅总结了液体火箭发动机涡轮泵低温轴承研制以及试验中的性能参数和故障模式特点,介绍了傅里叶变换、小波分析等多种数据分析方法,建立了仿真模型,开发集成了短时傅里叶变换、小波分析等多种方法的数据分析系统,对行业内发动机试验涡轮泵轴承数据分析提供了重要的参考依据[21]。

杨懿等介绍了小波去噪的基本原理、四种阈值去噪的基本方法以及具体实施的基本步骤。将信噪比作为选择小波基函数的参考标准,将相关系数作为去噪结果的评价标准。通过对发动机试验含噪流量数据进行去噪分析,证明小波分析方法能够有效消除流量数据中的含噪分量[22]。

白泉等介绍了小波分析在实际应用中的基本步骤和方法。小波分析中所用到的小波基函数具有非唯一性,采用不同小波基函数分析同样的数据时将会产生不同的结果。因此,研究人员列举了LP 小波、Meyer 小波、Db 小波等多种小波基函数在支撑长度、对称性和正则性等方面的特征性质,根据小波基函数性质和被分析数据的特征选择恰当的小波基函数[23]。

采用小波分析方法对某型号发动机试验关机段推力室脉动压力数据的奇异点特征进行分析。数据样本数量为4 000 个,采样率为10 kHz,选择DB9 小波小波基函数,分解层数为7 层,分解结果如图4 所示。

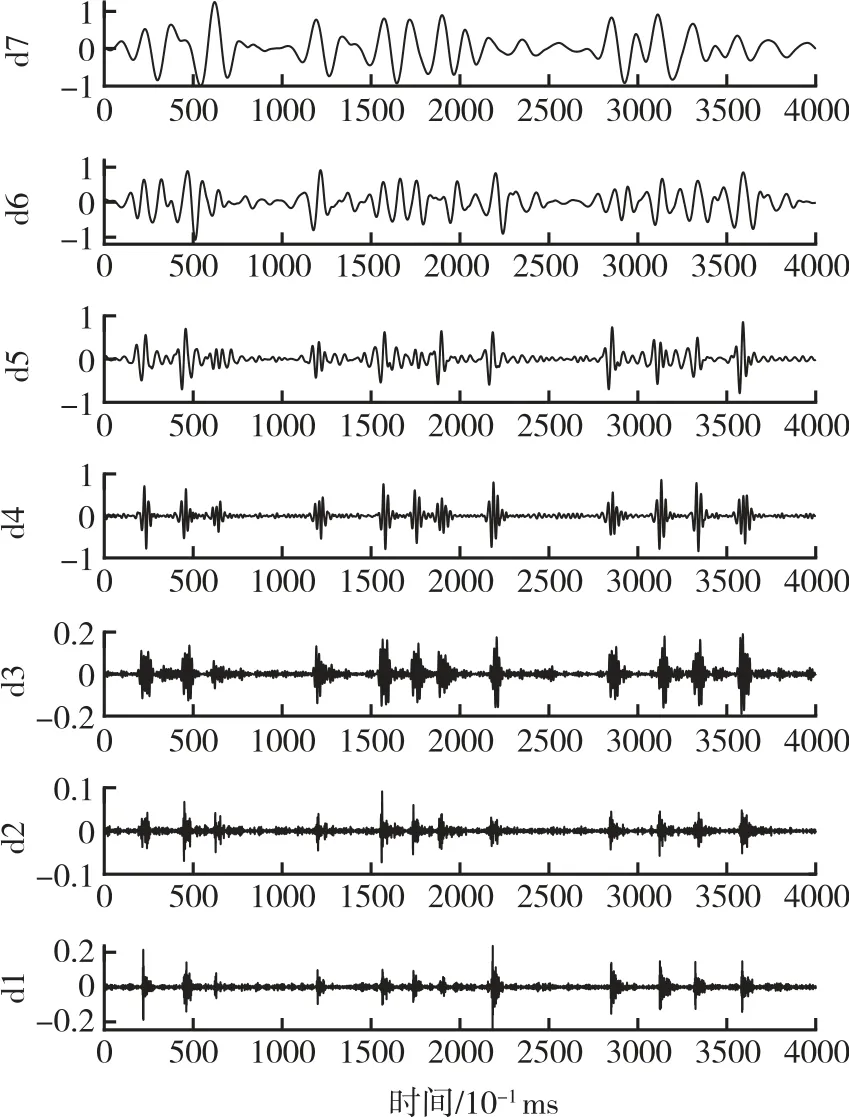
图4 DB9 小波7 层分解结果Fig.4 DB9 wavelet 7-level decomposition results

对图4 中d1～d7 的分解结果进行分析可知,小波分析能够准确定位数据奇异点在时域内的信息。d1～d5 层的分解重构效果较d6～d7 好,能够清晰观测到时域内不连续点和幅值变化信息。d1～d4 低层高频信号中突变能量较d5～d7 层高,包含了原始信号中大部分能量突变成分。随着分解层数的增加,小波分解过滤的信息较多,d6～d7 层存在一定程度的失真,曲线较为平缓,对分析结果的影响不大。在运用小波分析方法对数据进行分析的过程中,可以将流量、振动等其他数据有效结合,为判断不稳定燃烧状态及发动机整体和零部件性能提供重要的参考依据。

2.3 小波包分析方法

小波包分析方法是小波概念的优化和提升。该方法克服了小波变换在中、高频段频率局部性分析能力差的缺陷,对信号中的高、低频部分进行二次分解,从而进一步提高了信号的时频分辨率[24,25]。小波包分析在信号去噪、奇异点定位、数据压缩、图形处理和故障检测等领域有着广泛的应用。

杨懿等介绍了小波包分析的基本原理和小波包阈值去噪的基本步骤。在对氢氧火箭发动机试验流量数据进行去噪过程中,将信噪比和相关系数作为去噪效果的评价标准,取得了良好的去噪效果[26]。

杨懿等采用小波包阈值去噪与分解重构算法分析液体火箭发动机试验脉动压力数据。分析了脉动压力数据在高、低频段内的系数特征和能量分布情况。结合相应振动测点FFT 频谱特性对发动机在多个工况内的工作状态进行分析[27]。

崔建国等针对主燃油泵轴承损坏以及调节器故障引发的喘振问题,将小波包多层分解后的能量信号作为原始信号的特征向量,结合神经网络中的极限学习算法,建立主燃油泵的故障诊断模型,并将该模型与BP 神经网络模型进行对比验证。结果显示,该模型能够更加准确、迅速地实现燃油泵故障诊断[28]。

任学平等采用小波包分析方法对汽车发动机运行的含噪振动信号进行去噪处理。根据计算机仿真结果选定合适的小波基函数和分解层数,对降噪后的信号进行残差分析和统计量分析。降噪结果显示该方法能有效区分信号中的突变和噪声成分,具有良好的信噪分离效果[29]。

马建仓等为有效判断航空发动机故障类型,统计了5 种常见的航空发动机工作故障特征,将峭度指标、裕度指标、脉冲指标和有效值等时域指标作为评判发动机是否正常工作的参考标准。根据分解结果中高低频带的能量信息,绘制多层频带的相对能量分布图,并结合故障特征和时域指标,实现航空发动机故障特征的准确定位[30]。

小波包分析方法在动态数据分析中的使用方法和流程与小波分析基本一致。在采用MATLAB 实现编程分析中,调用的分析程序和基函数稍有不同。

以某型号发动机试验流量数据为例[26],采用小波包分析方法对含噪流量数据进行去噪分析。样本点数为8 000 个,数据采集系统采样率为10 kHz。原始数据如图5 所示。

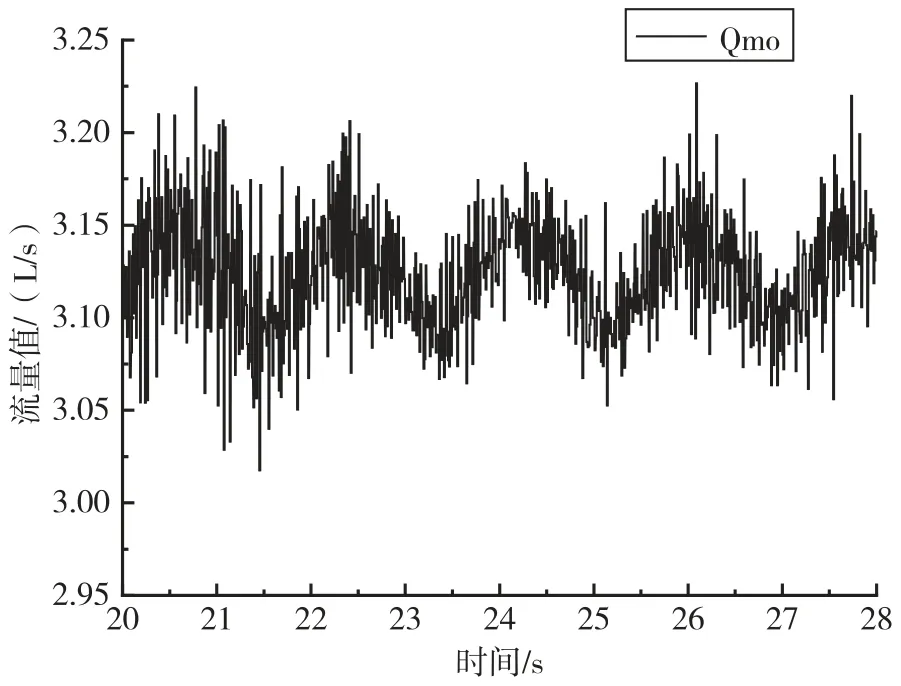
图5 含噪流量数据图Fig.5 Noisy flow data chart

分别采用默认阈值法和自选阈值法,对比分析Sym1～Sym9、DB1～DB9 和4～7 层分解结果的信噪比和相关系数的数据,采用Sym6 和Db5 小波基、自选阈值法、5 层分解对含噪数据进行去噪处理,分解结果如图6 所示。

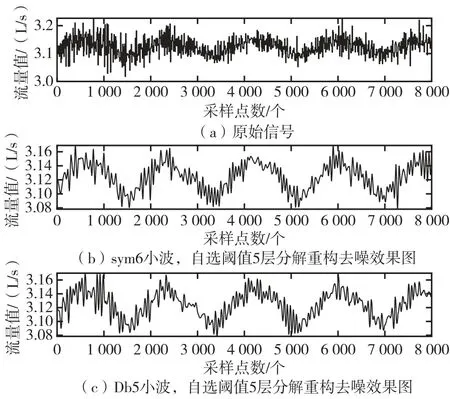
图6 Sym6 小波和DB5 小波分析结果图Fig.6 Results of Sym6 wavelet and DB5 wavelet analysis

通过对比两种小波包分解数据与理论值之间的相对误差,可以确定更符合实际情况的方法。

2.4 希尔伯特-黄变换分析方法

希尔伯特-黄变换(Hilbert-Huang Transform,HHT)由美籍华人Norden E.Huang 于1998 年提出[31]。HHT 分为两个部分:经验模态分解(Empirical Mode Decomposition,EMD)和希尔伯特谱分析。该方法克服了传统方法中用无意义的谐波分量来表示非平稳信号的缺陷,较高的时频分辨率和良好的时频聚集性适用于分析非平稳、非线性数据[32]。

EMD 给出了瞬时频率的定义,通过引进本征模态函数(Intrinsic Mode Function,IMF)实现非平稳线性信号的平稳化处理,再对IMF 进行希尔伯特变换得到不同特征尺度下的瞬时振幅和瞬时频率的关系,建立了谱分析与时域的对应关系,能够精确分析原始信号时频域的分布规律。但是在运用过程中也存在端点飞翼和模态混叠等问题。近些年来,有诸多研究人员对HHT 使用过程中的问题进行了更加深入的研究,并提出了相应的解决办法[33-37]。

符娆等采用HHT 方法从发动机转子振动信号中提取转子工作故障信息,并结合振动故障的机理,分析了发动机转子碰摩的主要特征。MATLAB仿真分析以及发动机试验转子振动数据的实例分析证明该方法能够对信号中的高低频分量进行分解。分解后的信号清晰显示了幅频域内的突变信息以及转子工作倍频与幅值的相关信息,为发动机故障定位提供了有力的参考依据。对发动机转子进行拆解后的分析也印证了该方法的有效性[38]。

李哲洙等采用HHT 分析方法对某型号航空发动机液压管路不同压力下的振动信号进行分析,EMD结果显示该方法能够过滤信号中的噪声分量,HHT边际谱能够清晰显示信号中的能量分布情况,为发动机液压管路的设计提供了重要参考依据[39]。

吴娅辉等针对传统分析方法无法区分航空发动机高低压转子和传动系统振动数据中多源数据混叠和噪声分量的问题,采用HHT 方法对混叠振动数据进行分解,借助统计学支持向量机分类方法研究了航空发动机小样本数据特征,为提取航空发动机故障特征,研判故障类型提供了有效途径[40]。

杨懿等分析了液体火箭发动机涡轮泵的故障机理,采用HHT 涡轮泵振动数据进行分析。采用信号包络非闭合镜像延拓的方法解决了EMD 过程中的端点飞翼的问题。根据Hilbert 能量分布频谱图和时频图能够对涡轮泵的故障进行有效诊断和分析[41]。

任刚等提出了一种基于EMD 的改进型变分模态分解方法。该方法将振动信号分解为若干分量,采用结合去趋势波动分析方法计算各个分量的尺度指数,设定相应的阈值,再对去噪后的分量进行重构。仿真和实测数据证明该方法能够识别故障信号,消除振动信号的背景噪声对振动信号的影响和干扰[42]。

高斌分析了希尔伯特-黄变换、小波分析和短时傅里叶变换等几种方法的优缺点。研究了基于HHT 对转子和滚动轴承故障进行定位和信息提取,通过EMD 得到各频率段分量,通过谱分析得到了故障的特征频率。通过对故障数据特征向量的提取和灵敏度分析,建立基于结构自适应网络模型,实现转子和滚动轴承故障的智能诊断[43]。

以某型号发动机试验稳定段推力室脉动压力数据为例,采用HHT 方法对数据进行分析。样本点数为2 000 个,数据采集系统采样率为10 kHz。4层分解结果如图7 所示。

分析图7 可知,EMD 能够有效提取脉动压力数据中不同频率段的信息,图7(a)～(d)显示了数据中频率从高到低的4 个分量,以及数据对应的相对幅值的大小。其中,IMF1～IMF4 阶分量在原始信号中所占的比重依次降低。IMF2～IMF4 分量的幅值波动趋势要大于IMF1 分量的波动趋势[32]。图7(e)为信号中存在的无关缓变低频分量,不影响数据分析。

对IMF1～IMF4 阶分量进行Hilbert 变换,变换后的Hilbert 谱分别对应第1 层～第4 层时间-频率曲线,如图8 所示。

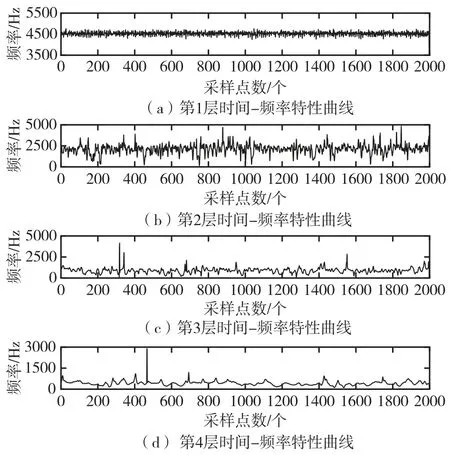
图8 IMF1～IMF4 时间-频率曲线图Fig.8 IMF1～IMF4 time frequency curve

分析图8 可知,第1 层～第4 层时间-频率曲线显示了脉动压力数据在全时域内的频率信息。分析第1、2 层时间-频率曲线,3 500～5 000 Hz 左右的中频带所占比重最大,1 500 Hz 以下的低频带所占的比重较小。第1 层时间-频率曲线中,全时域内,频率变化趋势较为平稳,没有明显的频率突变点。第2 层～第4 层时间-频率曲线显示在全时域内存在多个频率突变峰值。结合脉动压力测点上下游对应的温度、压力测点、试验时序和试验工况等多重信息,为评判发动机燃烧状态提供重要的参考依据[32]。

2.5 多种方法相结合进行分析的方法

2.1 ～2.4 节介绍了4 种常用的动态数据处理方法,在实际应用中,研究人员可以根据数据的特征和分析方法的优缺点将几种方法相结合进行数据分析,实现深度挖掘数据信息,提高数据分析的精度和效果的目的。近年来,有多位研究人员就多种方法相结合进行数据分析开展了研究工作。

徐平平等采用小波分析和HHT 相结合的方法对喷嘴腔内自振射流的脉动压力进行分析,对比了两种方法在压力特征信号提取和时频分析方面的特点,分析结果表明两种方法在信号分解重构方面都具有自身的特点:小波分析方法能够较好消除信号中的高频噪声分量,但在信号提取方面的能力不如HHT 方法;HHT 方法在信号提取信号特征、消噪和突变点检测方面更具有优势[44]。

熊星、苏涛等针对传统时频分析方法的局限性和HHT 在自适应性、完备性和正交性方面的优势以及HHT 在模态混叠和低频分析过程中产生内禀函数的问题,将小波分析方法和HHT 方法相结合,分别采用小波分析和HHT 分解依次对信号进行第1、2 层分解、筛选和重构。根据Hilbert 谱和Hilbert边际谱的分析结果对滚动轴承的故障进行诊断[45,46]。

马引刚等将HHT 理论中的EMD 方法和独立成分分析方法相结合,先对火箭发动机多模式组合故障的振动信号进行EMD 分解,得到多个不同尺度下的IMF 函数,再用独立成分分析方法分离出各振源的独立响应特征分量。通过实例分析,验证了该方法能够从振动数据中有效提取多源振动分量信号特征[47]。

崔建国等为便于提取舰用发动机主泵轴承的振动数据特征,采用小波包分析和支持向量机相结合的分析方法对轴承故障振动数据进行分析。小波包高、低频段细化分解获取振动信号的不同故障模式下的能量特征。支持向量机对不同故障特征向量的训练和分类实现对不同故障的诊断和分析。试验验证结果也表明该方法能够精确识别诊断信号中不同的故障信息[48]。

司景萍等采用小波包分析和人工神经网络相结合的方法对发动机故障进行有效诊断和分析,建立发动机正常工作和异常故障振动数据库,采用小波包对振动数据进行分解重构,提取表征发动机工作的特征向量作为神经网络分析训练和检验的数据样本,通过神经网络的训练,能够精确识别发动机工作的故障信息[49]。

高远为提取发动机不同工作状态的特征信息,采用小波包能量熵和经验模态分解能量特征分析的方法提取发动机正常工作和故障工作振动信号中的特征向量,再采用支持向量机、分类器和极限学习网络等人工神经网络方法,建立不同工作状态的数据模型。验证结果表明该方法能够实现不同工况的识别和分类[50]。

3 结束语

针对发动机动态数据分析处理的实际需求,详细分析和介绍了FFT、小波分析、小波包分析和HHT 等几种适用于对发动机振动、脉动压力等动态数据进行分析处理的方法及其优缺点。介绍了多种方法在实际使用过程中的分析流程,并对试验数据进行了实例分析。对研究设计人员分析发动机试验动态数据、挖掘数据信息和优化设计提供了参考依据。