旋转惯导中转位电机控制算法对导航精度的影响分析

梁洪涛 ,王一兵 ,朱燕萍 ,任 晖 ,何绪龙

(1.海装驻北京地区第一军事代表室,北京 100076;2.北京航天发射技术研究所,北京 100076;3.北京航天计量测试技术研究所,北京 100076)

1 引言

为满足海用导航和陆用定瞄系统的长时间热待机、惯组高精度快速对准等需求,在定位、定向系统中,旋转式捷联惯导逐步得到应用和推广[1-8]。旋转式捷联惯导内置有一套或者两套转位机构,在惯导初始对准或长时间导航过程中,转位装置用于驱动惯性测量单元(IMU)转动[10,11]。而转位电机控制算法与导航算法耦合度较大,控制算法需满足导航解算在不同使用工况下的需求,主要集中在三个方面:

(1)在初始对准中,为压缩对准时间,需要转位装置在较短的时间内转到指定位置。如5 min 初始对准时间中有4 次转位时间预留,压缩每次转位时间到6 s,可缩短对准时间。

(2)在导航过程中旋转调制,需要采用两位置对消的方式来减小陀螺和加速度计的误差,以便提高导航解算的准确度[5-7]。因此,需要IMU 的转动加速和减速过程对称。否则,姿态解算结果中会因不对称性而产生附加误差。

(3)在姿态解调时,需要减小角加速度的变化[7-9]。由于IMU 的姿态角和转位机构测角数据之间同步时差为5 ms,转速存在500°/s2的角加速度时,带入的解调误差为22.5″。显然,这在高精度的定位定向系统中是不能容忍的。

由此可知,旋转惯导中IMU 转位机构控制需要速度平稳和加速度可控。基于此,首先分析了现有的分段速度控制方法对导航精度的影响;然后,提出了S 曲线控制算法用于抑制电机控制引入的导航误差和不利因素,并根据不同工况进行了参数计算和轨迹规划研究;最后,为验证理论分析开展了分段速度控制算法和S 曲线控制算法的对比试验,测试了不同控制算法对转位电机控制效果。

2 转位电机分段速度控制法分析

转位控制系统中,内环为框架速率环,外环为位置环[11,12],如图1 所示。通过位置环和速率环双环复合控制驱动转位机构带动IMU 转动,利用电机控制板实现角度和控制信号的采集、滤波计算、控制参数计算以及生成脉宽调制(PWM)控制信号,按照控制目标驱动电机实现对转位装置的速度和位置的控制[5]。测角系统是转位控制系统的角度测量装置,主要用于对轴的角位置进行测量,作为反馈环节参与大系统的控制。

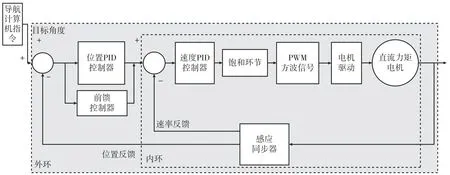
图1 系统控制框图Fig.1 Block diagram of motor control system

现有转位电机轨迹规划采用的是分段速度控制法,如图2 所示,将转动角度分为三段:(1)在Ts1时间段,即电机收到转位指令到转位至距离终点10°的位置,位置环输出为最大转速vs1=45°/s;(2)Ts2时间段,即终点前10°到终点前1°,位置环输出转速vs2=10°/s;(3)Ts3时间段,即终点前10°到终点前1°之内,位置环采用比例、积分和微分算法输出速度控制量vs3。

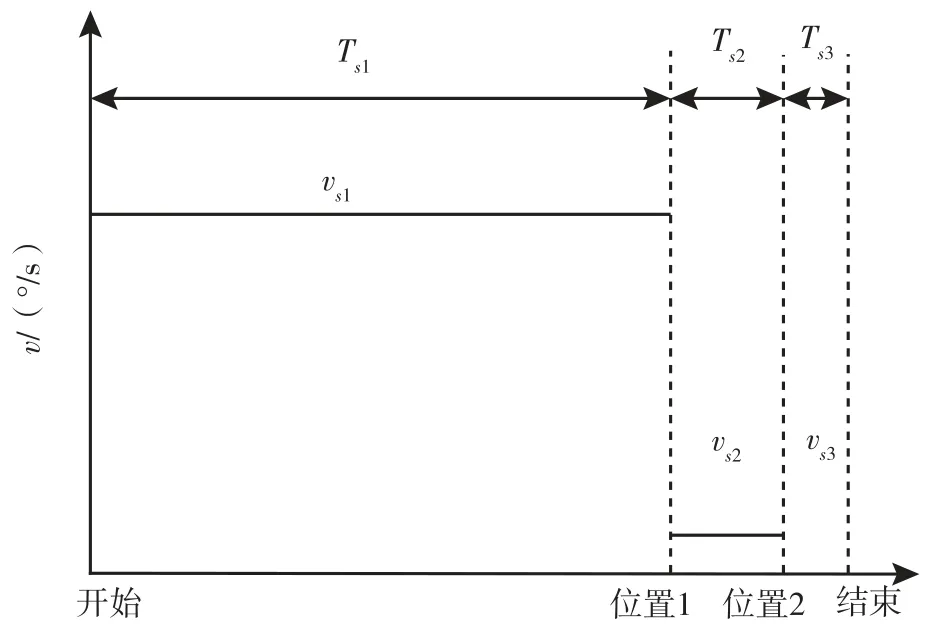
图2 分段速度控制Fig.2 Segmented speed control method

从分段控制的速度可以看到,存在多次速度控制跳变,如控制开始时刻、距离终点前10°位置时刻和距离终点前1°位置时刻,控制速度跳变要求很大的加速度控制,瞬间加速度会大于100°/s2。这种控制方法主要存在两个问题:(1)加在电机上的电流出现剧烈跳变,对驱动放大器、电机电刷等造成损伤;(2)速度跳变对速度环的控制相应能力要求很高,容易出现超调和震荡。

3 转位电机S 曲线控制算法分析

3.1 S 曲线加减速控制原理

S 曲线加减速方法是在直线加减速控制方法的基础上引入角加加速度(角加速度的微分) 约束[13-17]。完整的S 曲线轨迹规划函数包含加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段七个部分,如图3 所示[18,19]。其中,s、v、a和j分别表示转位的角度、角速度、角加速度和角加加速度,tj为匀加加速时间,ta为匀加速度时间,tv为匀速时间,t0～t7为S 曲线轨迹中各时刻点。

图3 S 曲线轨迹规划轮廓图Fig.3 S-curve trajectory planning diagram

惯导中电机加减速始末速度为零。由运动学方程可求得7 个阶段所对应的a、v和s与t之间的公式。在t1时刻,对应的加速度a(t1)、速度v(t1)和位置s(t1)按公式(1)～公式(3)计算。

式中:jmax——最大加加速度。

在t2时刻,对应的加速度a(t2)、速度v(t2)和位置s(t2)按公式(4)～公式(6)计算。

逐次递推,推导出t3、t4、t5、t6,得到在转位结束时刻t7的方程如公式(7)～公式(9)所示。

3.2 轨迹规划参数设计

根据转位机构的硬件特性给出相应的运动学限制条件:如最大速度限制vmax,最大加速度限制amax以及最大加加速度限制jmax。tj受amax和jmax约束,ta受vmax和s约束,而tv则仅受s约束,建立三种约束准则来求取ta、tv和tj的值。考虑ta和tv计算tj,则:

若ta由速度约束来确定,即不存在匀速段,可得tv=0,否则,可得

S 曲线轨迹规划算法按照上述要求进行设计,对于转位设定好vmax、amax和jmax后,通过算法均能解算出一组轨迹规划参数,参数包括每个时间点对应的速度和位置信息。

3.3 电机S 曲线规划结果

在实际应用中,电机的控制通过数字控制器实现,需要对运算结果进行离散化。设置起始点、终点、最大速度、最大加速度和最大加加速度,规划出S 加减速曲线。依据tj不同的约束条件,可分三种情况讨论。

(1)情况1 电机控制规划

在情况1 中,电机转动中存在匀加加速度、匀加速度和匀速阶段。设置起始位置为零,转位终点为180°,转位最大速度为60°/s,加速度为60°/s2,加加速度为60°/s3。转位时间为t,转位结束后的误差为error。规划结果如表1 和图4 所示。

表1 情况1 轨迹规划离散结果Tab.1 Discretized planning result for case 1

图4 情况1 的S 曲线规划结果Fig.4 S-curve planning result for case 1

(2)情况2 电机控制规划

在情况2 中,存在匀加加速度和匀加速度阶段,但是不存在匀速阶段。设置转位机构转位起始点为零,转位终点为90°,转位最大速度为60°/s,加速度为60°/s2,加加速度为80°/s3。对所有被规划参数进行离散化处理,规划后的结果如表2 和图5所示。

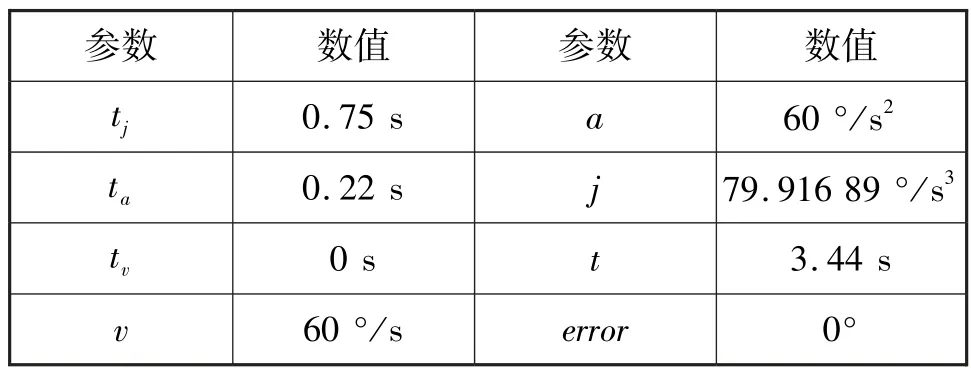
表2 情况2 轨迹规划离散结果Tab.2 Discretized planning result for case 2

图5 情况2 的S 曲线规划结果Fig.5 S-curve planning result for case 2

(3)情况3 电机控制规划

在情况3 中,存在匀加加速度阶段,不存在匀加速度和匀速阶段。设置转位机构转位起始点为零,转位终点为30°,转位最大速度为60°/s,加速度为60°/s2,加加速度为80°/s3。规划结果如表3 和图6 所示。

表3 情况3 轨迹规划离散结果Tab.3 Discretized planning result for case 3

图6 情况3 的S 曲线规划结果Fig.6 S-curve planning result for case 3

上述三种情况下的轨迹规划结果显示,所提出的方法避免了传统分段速度控制中的不利因素,满足旋转式惯导对电机控制的平稳性和对称性的要求,有利于提升惯导的精度[20-22]。

4 对比试验

为验证所提S 曲线控制方法的有效性,开展对比试验。在同一个电机驱动电路中,分别采用传统的分段速度控制方法和所提出的S 曲线控制方法,测试转位机构的性能参数。

使用分段速度控制方法进行控制,设置最大转速为60°/s,目标位置为245°。实时监测转位机构的转位、角速度和角加速度,采样频率为100 Hz,测试数据曲线如图7～图10 所示。

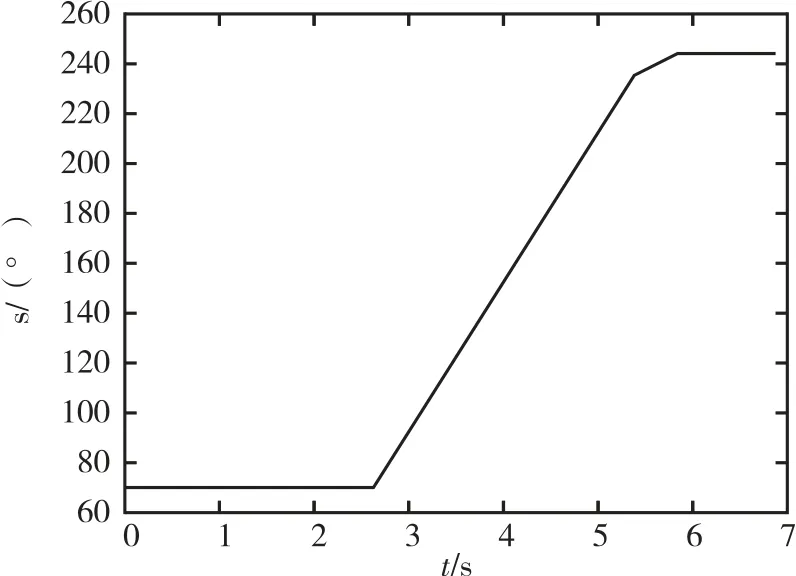
图7 分段速度控制方法位置曲线Fig.7 Angle curve in segmented-speed control method

通过对测试结果分析可知,整个转位过程持续时间约为4.5 s。将图7 中曲线局部放大如图8 所示,在转位机构转到终点时,存在0.5°的角度超调,震荡调整时间约为1 s;从图9 所示的转速曲线可以看出,转速控制有明显超调,最大转速超出目标转速约12°/s,变速结束后,转速出现较高频率的震荡,如图中方框标记,加速和减速过程不对称;从图10 中的角加速度曲线可以看出,在转动开始时刻、距离目标转位10°时刻和转动结束时刻的三个时间点,加速度跳变过大,瞬间加速度可达1 000°/s2。

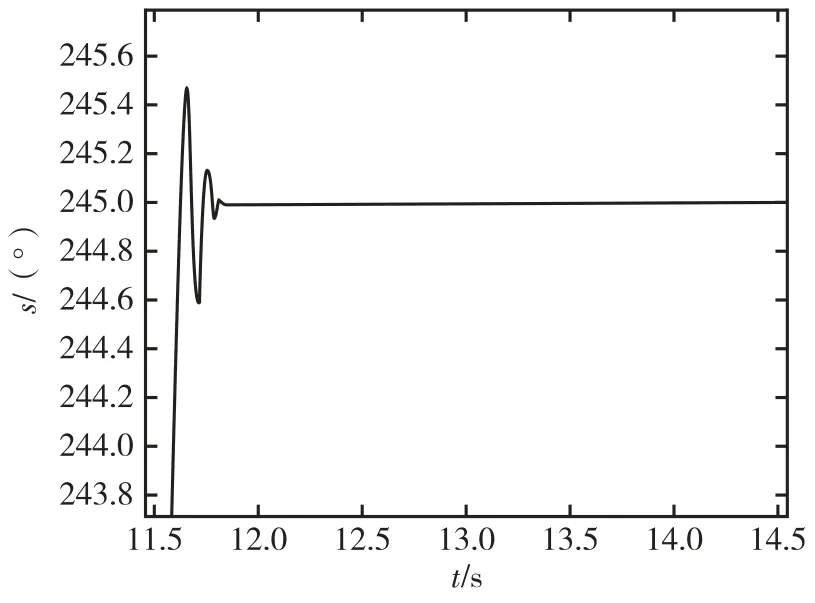
图8 分段速度控制位置曲线超调Fig.8 Angle overshoot in segmented-speed control method

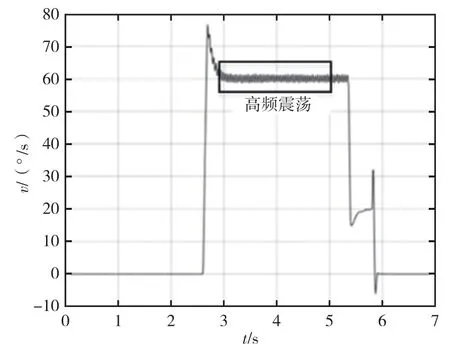
图9 分段速度控制方法速度曲线Fig.9 Rotation rate in segmented-speed control method

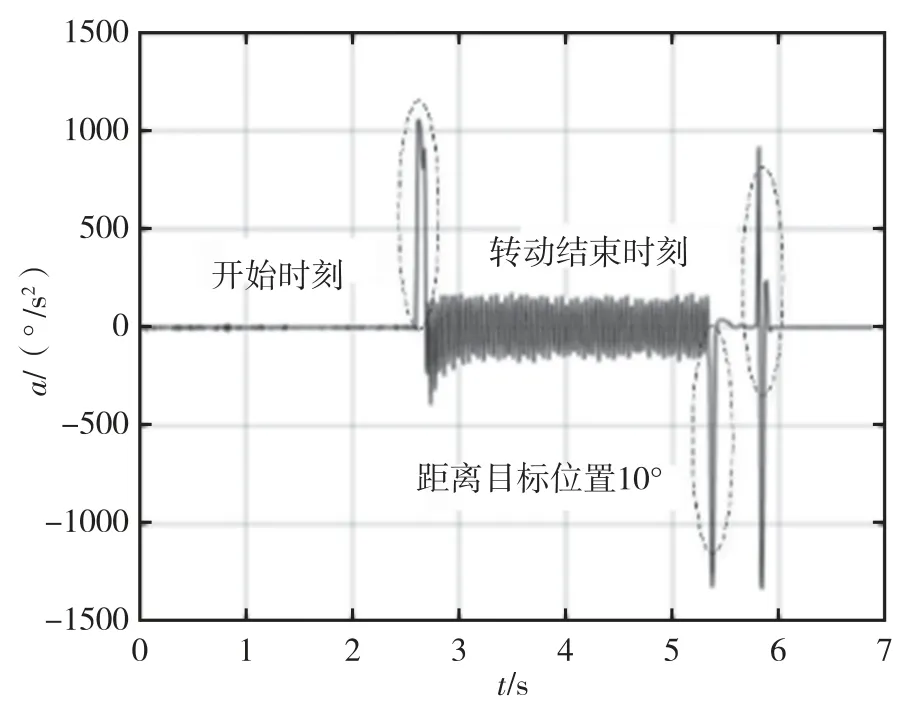
图10 分段速度控制方法加速度曲线Fig.10 Angular acceleration in segmented-speed control method

使用同一个试验设备,改用S 曲线加减速控制算法进行试验。设置最大转速为60°/s、加速度为60°/s2、加加速度为60°/s3、目标角度为245°,测试加减速过程中的位置、速度和加速度曲线如图11～图13 所示。

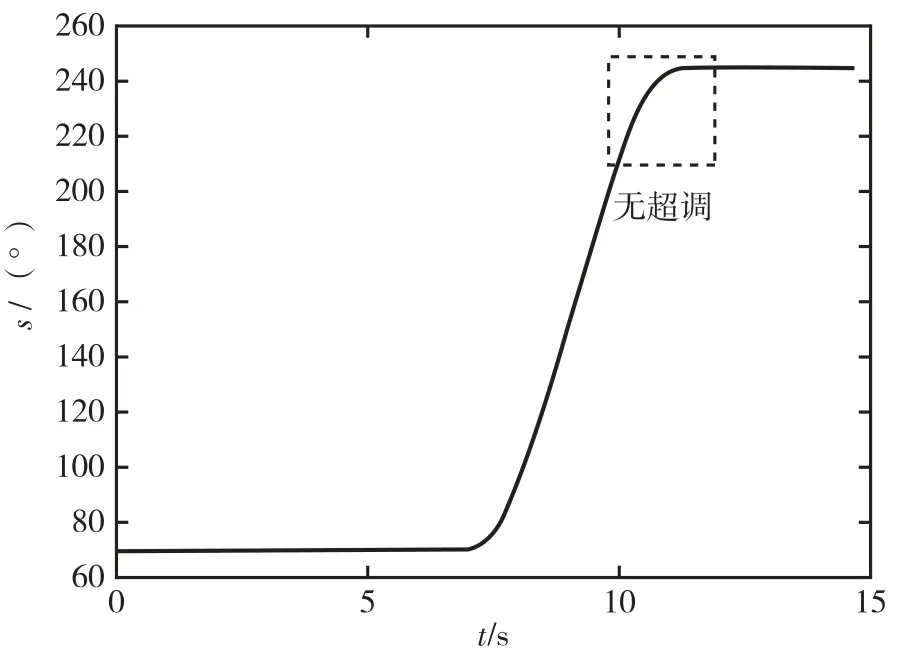
图11 S 曲线控制位置曲线Fig.11 Angle in S-curve control method

图12 S 曲线控制角速度曲线Fig.12 Rotation rate in S-curve control method

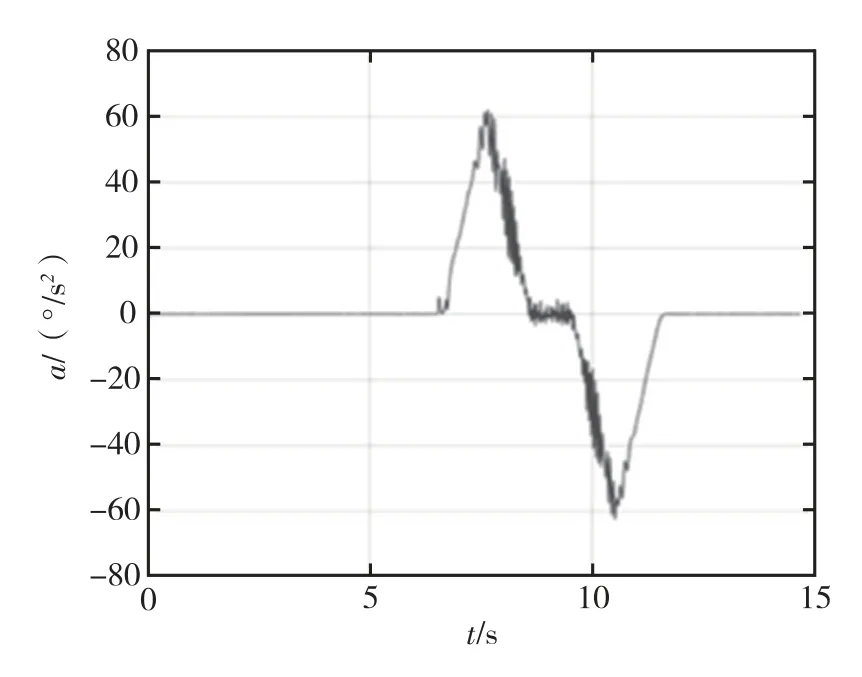
图13 S 曲线控制角加速度曲线Fig.13 Angular acceleration in S-curve control method

试验中,转位到目标角度用时约5 s。通过与分段速度控制方法对比可知,S 曲线控制方法具有以下特点:(1)转到终点时,位置超调量接近零,几乎没有震荡时间,如图11 和图14 所示;(2)变速过程中,转速按照预设的S 曲线进行加减速,角速度过渡平稳,没有明显超调和振荡,并且转速加减速过程对称,如图12 和图15 所示;(3)转动过程中角加速度可控,最大不超过60°/s2。

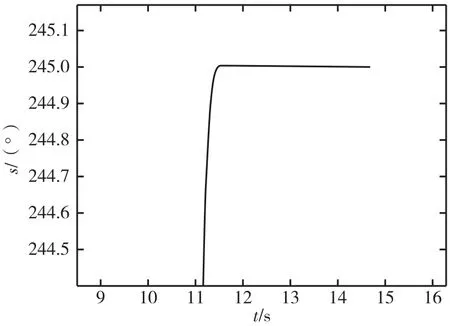
图14 S 曲线控制位置超调Fig.14 Angle overshoot in S-curve control method

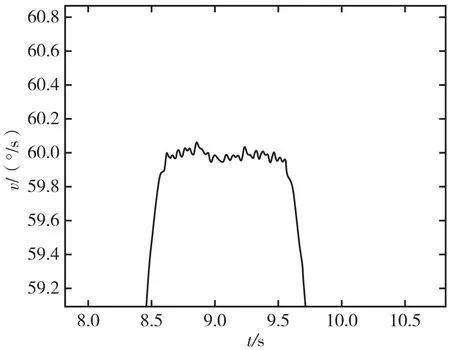
图15 S 曲线控制速度超调Fig.15 Rotation-rate overshoot in S-curve control method

5 结束语

针对高精度旋转式惯导工作特点,分析表明转位机构电机控制需要保证平稳性、对称性和角加速度可控。理论分析现有的分段速度控制方法对导航精度的影响,并通过引入角加加速度约束控制电机加减速过程,提出了一种基于S 曲线的电机转位轨迹规划方法。通过对比试验,验证了S 曲线控制方法能够减小位置和速度的超调和震荡,保证了加速和减速过程的对称性。该方法从电机驱动角度出发,有效地抑制了电机控制在旋转惯导中引入的调制误差,对高精度惯导精度提升具有一定的工程意义。