高精度主给水超声波流量计的不确定度分析方法

刘 岩 ,魏华彤 ,白 天 ,王枫宁 ,任大呈 ,刘 莉 ,崔希炜,郭 林

(1.阿米检测技术有限公司,北京 100076;2.中国核电工程公司,北京 100840;3.北京航天计量测试技术研究所,北京 100076)

1 引言

超声波流量测量作为当前流量测量相关领域的主要技术之一,与其他种类流量计相对比,基于该技术的流量计具有计量精准、稳定性强、成本低、产品寿命长及维护便捷等优点,特别是在中、大口径管道流量计量、复杂工况条件和特殊被测流体介质等领域,已有成为更优选择的趋势。

核反应堆堆芯功率是保证发电量的核心,对堆芯功率的准确测量是在确保核安全情况下提升发电功率的关键。对于华龙一号等新一代压水堆核电机组,反应堆堆芯功率是通过测量二回路上蒸汽发生器主给水流量和其他参数,再利用热平衡模型计算获得,因此,主给水流量的精确测量是提高发电功率的重要保障。

然而,超声波流量计因其本身的测量原理而存在各种限制性因素。由核电机组主给水高温高压的特点带来的误差包括复杂温度压力变化所引入的流场流速分布变化和管段几何变形,由管道本身制造工艺和安装环境造成的误差效应,以及电路增益放大与响应精度等[1],此类误差在国内尚无高温高压实流标定台架的条件下,尚未形成一种可行的不确定度计量溯源技术。

基于超声波测量技术的流量计是一个多元素技术融合的复杂计量器。从超声波流量计测量的原理出发,对不同声道下的流量计测量方法进行了研究,将单声道与多声道流量计不确定度分量计算方式相结合,全面分析了多声道形式的管道以及壁面的流体流场分布情况。在渡越时间方面,通过信号传输原理,将时间项逐一分解评估,并给出了相应的测量方法。量化了由制造工艺及温压变化所引入的声道几何因子和管道截面积的不确定度分量,并分别评估了其精度控制因素。

2 时差法超声波流量计测量原理

超声波流量计通过测量超声波换能器在流体介质中所发射和接收的超声波速度差来测量流体的流速,进而计算体积流量。基于时差法的流量计通过测量超声波脉冲在流体流动方向和逆流动方向的传播时间之差,得到沿声波路径的流体平均流速。

时差法的超声波流量计在气体及液体流量测量方面有着测量准确度高、特大流量及腐蚀性介质的高精度测量等优点,因此,被广泛用于特殊流量测量领域,例如,核电厂主给水测量及废水厂排污测量等方面[2]。

流量计测量精度除受本身硬件电路设计所产生信号传输等方面的影响之外,基于流体的声学特性也受到被测介质本身流场、温度、密度、粘度和悬浮颗粒的影响,此外,影响其测量精度的主要因素还包括流量计本身测量环境温度和压力变化而带来的管段形变量[3]。

2.1 超声波时差法原理

时差法超声波流量计的测量原理是获得超声波脉冲随流动方向传播和逆流方向传播的传输时间之间的差异,通过上游绝对传输时间tup和下游绝对传输时间tdown,解算出管内的平均流体流速v和声速C[4]。

设定接收和发射换能器之间的距离为L,声道倾角为θ,超声波从流动方向的上游换能器发射到下游时与流体介质流动方向相同,从下游到上游时与流动方向相逆,如图1 所示。

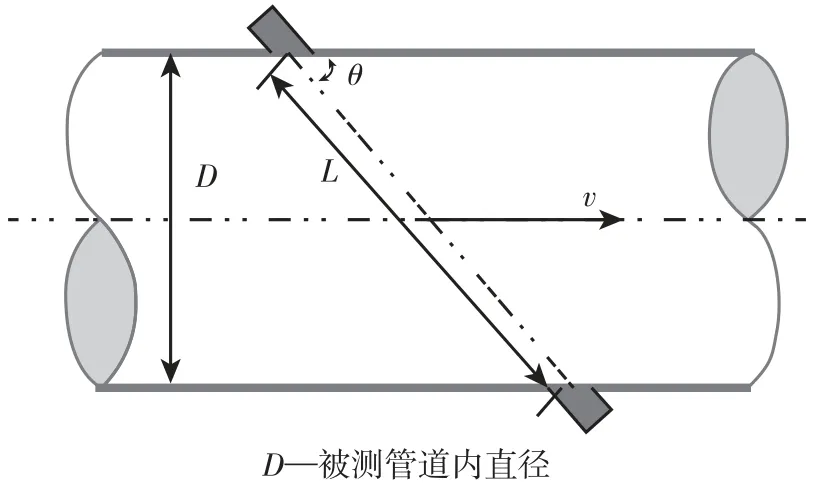
图1 流量计单声道上流速的测量示意图Fig.1 Schematic diagram of velocity measurement on single channel of flowmeter

进而得出流体流速的表达式[5]

式中:vi——第i条声道的流体流速。

对于单声道流量计,截面平均流速与该声道上求出的流速存在特定关系,但易受到流速分布廓形的影响。为了提高流量计的测量准确度,在待测截面上布置通过流量积分方法所得的多条声道,如图2 所示。

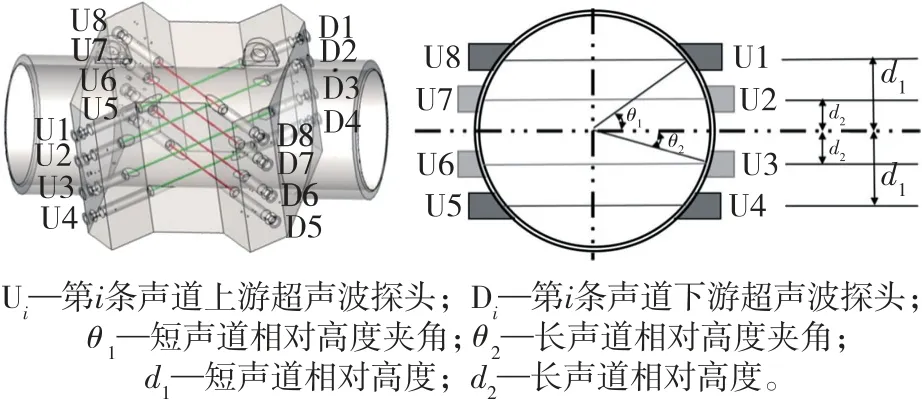
图2 多声道布置结构外视图Fig.2 Exterior view of multi-channel structure

将测得的多个声道的流体流速vi利用数学的函数关系联合起来,可得到管道平均流速的估计值,通过合适的积分方式,乘以过流面积A及流体密度ρ,即可得到质量流量Qm,即[6]

式中:KP——流速剖面修正系数;ωi——基于所采用的积分算法得出的第i条声道的权重系数。

2.2 测量不确定度分析研究

在分析了测量不确定度来源后,有针对性地对各分量进行研究内容的分解,ρ、v和A可作为渡越时间与声道长度的分解,因此,在良好的流量测量应用方面之外,也能够通过不确定度分析的研究建立高精度主给水超声波流量计的计量溯源方法。从超声流量计的结构和测量原理出发,其测量不确定度来源可分为三类:

(1)几何量:与测量管段的机械几何尺寸有关;(2)力学量:与被测流体的流速流态分布有关;(3)时间量:与测得的传播时间有关。

2.2.1 单声道超声波流量计不确定度分量分析

按公式(4)使用单声道超声波流量计进行质量流量的测量,可以将之改写为

式中:Qm,s——单声道流量计质量流量。

从公式(6)中可知,质量流量的不确定度来源有:ρ、D、L、θ、tup和tdown。

2.2.2 多声道超声波流量计不确定度分量分析

多声道超声波流量计的质量流量计算公式(6)可改写为

式中:Qm,m——多声道流量计质量流量;tup,i——第i条声道的上游绝对传输时间;tdown,i——第i条声道的下游绝对传输时间;Li——第i条声道的长度;θi——第i条声道的倾角。

从公式(7)可知,多声道超声波流量计质量流量的不确定度来源有:ρ、D、KP、ωi、Li、θi、tup和tdown。

D、L和θ的不确定度可以归结为管道几何量。对于多声道超声波流量计来说,为了提升其测量精度或满足在高温高压等复杂工况下运行的情况,其管道几何量由于工况、流体介质等因素产生的形变所引入的不确定度分量可单独分析。此外ωi也可从算法的角度单独分析。因此,流量计的测量不确定度分解如图3 所示。

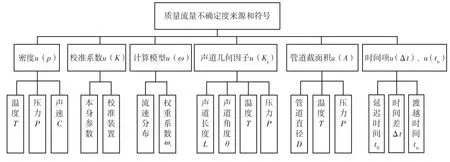
图3 不确定度分解示意图Fig.3 Schematic diagram of uncertainty decomposition

质量流量不确定度按公式(8)计算。

3 不确定度分量的量化分析

通过超声流量计的结构和测量原理,分析测量不确定度来源,从不确定度各分量的内容分解出发,对不同分量进行逐一量化分析,并对各不确定度分量的计算方法给出评估建议,最终合成超声波流量计的测量不确定度。

3.1 密度引入的不确定度分量u(ρ)

在计算质量流量时,密度是与被测流体直接相关联的分量。由于主给水是经过处理的纯水,其密度、声速通常受温度和压力的影响,因此可将密度看作是压力P和温度T两个基本分量的函数,P可通过压力变送器测得,T可以通过温度变送器或声速C获得,如图4 所示。

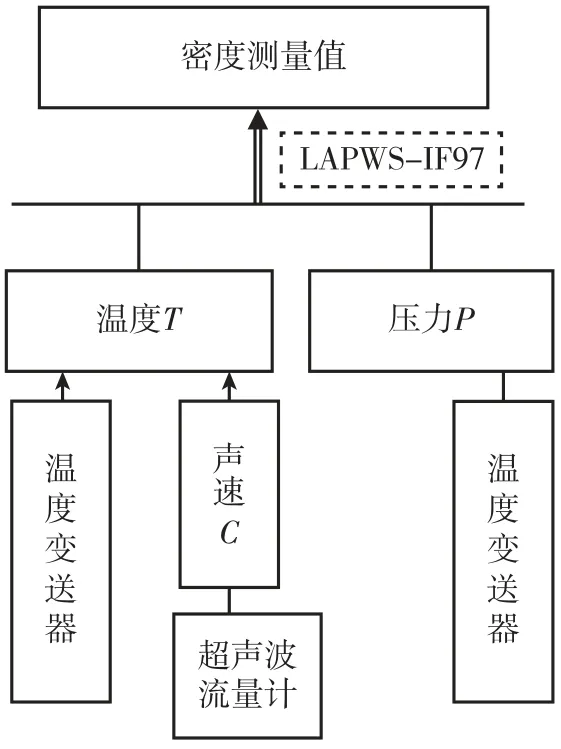
图4 密度求解流程图Fig.4 Flowchart of density solution

当T与P可通过变送器测得时,利用“国际水和水蒸气性质学会工业用计算公式1997 水”(IAPWS-IF97 公式)可进行密度求解。

式中:π=p/p∗,p∗=16.53 MPa;τ=T∗/T,T∗=1 386 K;R——空气常数,R=0.461 526 kJ·kg-1·K-1。变量π是压力的函数,τ是温度的函数,γR是压力和温度的函数。

温度间接测量法首先通过C获得T,然后结合公式(11)求解ρ。

其中,变量γR、γRτ、γττ、γRR均是压力和温度的函数。

密度不确定度分量u(ρ)来源于T和P的测量不确定度。由于T和P之间函数关系复杂,无法直接建立ρ与T、P之间的不确定度合成公式。因此,可通过试验测量与A类标准不确定度计算公式对此类密度值的试验测试结果进行不确定度分析。

式中:ρi——第i个流量点密度测量值;ρi,j——第i个流量点第j次密度测量值——第i个流量点密度测量平均值。

3.2 校准系数引入的不确定度分量u(K)

流量校准系数的不确定度一部分是校准装置带来的,另一部分取决于被测仪表本身性能。假设校准装置的扩展不确定度U=0.05%(k=2),校准温度为25℃,在常压下,校准系数引入的相对不确定度分量为

式中:Kij——工况i下第j次测量的校准系数。

3.3 计算模型引入的不确定度分量u(ω)

超声波流量计是通过计算测流管段上整体流量的平均流速来得到流量信息的,然而在具体应用中,由于被测流体在主给水测量管道中的流速分布呈现并非理想的均匀状态,因此,多声道超声波流量计虽能够解决单个声道的超声波流量计关于流速分布修正的问题,但仍须使用积分权重技术来确定多个声道的分布。目前被广泛认可和应用的超声流量计积分方法有Gauss-Jacobi 和OWICS 两种积分方法。以双侧8 声道(单侧4 声道)超声流量计为例,Gauss-Jacobi 与OWICS 两种积分方法确定的声道高度和权重系数如表1 所示。

表1 Gauss-Jacobi 和OWICS 的声道高度与权重系数Tab.1 Track height and weight coefficients of Gauss-Jacobi and OWICS

积分方法主要用于降低流动干扰和非理想流场的敏感性,二者主要来源于流体流动状态及流场环境条件带来的影响。研究表明,当管内流体处于层流的流动状态时,管内流体流速是以管中心线为中心轴对称分布,其最大流速出现在管中心线上。在管内流体转为紊流状态时,受流场环境影响,在流场充分发展的环境下,管内流体流速是以管中心线为中心形成最大流速并向外对称分布,其分布为指数形式,近壁层流层随流速增加而逐渐变薄;而在没有充分发展或接近弯管的环境下,其最大流速将出现在弯管外侧,其管内流速分布同样随雷诺数变化而有较大变化。

此外,目前工业领域使用的大口径多声道超声波流量计通常具有良好的流场环境条件,测量管段前后都有较为充分的直管段长度。而中型及小型口径超声波流量计除几何量与时间量的影响外,其测量准确度受非理想流场条件所引入的力学量影响较大。对于流场条件的部分研究表明,在上游直管段长度为1D(1 倍管段直径)至10D时,超声波流量计将随着与弯管处的距离的增加而准确度上升,当上游直管段为10D至30D时,测量准确度随着距离增加而逐渐趋于稳定上升,例如单声道超声波流量计上游直管段长度为19D时,其误差可控制在5%以内[7],直至上游直管段为30D及以后,其管内流体流速可形成较为固定的流速分布状况。因此在JJG1030 规定及A.G.A.9 报告中均建议,在不安装流动调整器的情况下,多声道超声流量计上游直管段长度至少为10D,下游直管段长度至少为5D,以保证流量计流场的充分发展[8]。

在流量计实际应用中,受到其安装环境和其他流动干扰因素的影响,其测得流速很难与实际流速一致,尤其是测量管段上游的弯管、阀门等扰流装置都会造成流体流动状态及流场环境条件的较大变化,从而导致流速剖面修正系数的较大误差等。这些因素都可以归入流速分布引入的不确定度分量。对其进行评定时,在有条件的情况下仿照现场实际安装运行环境搭建标定台架,进行实流校准。在条件不足时,可通过CFD(Computational Fluid Dynamics,计算流体力学)仿真技术进行建模计算来预估,也可以得到一个相对合理的分布区间[9]。

3.4 声道几何因子引入的不确定度分量u(Kg)

除内径外,换能器间的声道长度、安装方位角等因素,以及这些因素在复杂工况下(温度压力变化时)由于壳体变形而导致的变化,也是流量测量的不确定度来源之一。

在温度与压力的作用下,表体在径向和轴向产生形变。径向变形直接影响D,轴向变形直接影响L,径向和轴向变形的综合效果影响θ。由公式(19)可知,θ与L的改变将对流量测量结果引入误差。

表体变形导致的声道长度和角度的改变往往同时发生,可用声道几何因子u(Kg)统一表示。实测时角度无法直接测量,可根据结构特点将角度转化成长度量的比值处理,则

式中:La,i——第i条声道长度沿管道轴向上的投影长度,La,i=Li×sinθ。

通过不确定度分解运算,有

其中,由声道长度和其投影长度引入的不确定度分量可通过公式(22)计算得出,各分量引入的误差按均匀分布考虑。

式中:PL——声道长度的测量误差;PL,S——通过仿真获得的变形量的误差。

3.5 管段截面积参数引入的不确定度分量u(A)

在超声波流量计加工设计以及测量过程中,管内径会对测量结果造成直接影响。在机械加工时,测流管段体内径加工误差应控制在±0.1 mm,按均匀分布考虑,测流管段的横截面积需稳定、明确。由于表体的内截面会随着压力和温度的变化而发生变化,任何直径上的变化会导致面积的变化,如果不加以修正会导致更大的流量误差[10]。

对于管段截面积参数引入的不确定度分量u(A),可通过对管段内径加工误差和内径受温度压力影响变化量的仿真误差综合评估,计算得到表体截面积变化引入的相对不确定度分量。

式中:PD——测流管段体内径加工误差,按均匀分布考虑;PD,S——通过仿真获得的变形量的误差,按均匀分布考虑。

3.6 时间项引入的不确定度分量u(Δt)和u(ttr)

作为超声波流量计的主要测量量之一,渡越时间是指超声波信号渡越声道所经过的时间,它是影响流量计测量准确性的关键因素,在实际系统中,时间项的测量主要由激发及接收的超声波信号计算得出,如图5 所示,因此,超声波信号除了要有可满足接收和信号处理单元的质量要求,还须兼顾传输时间的准确性要求。

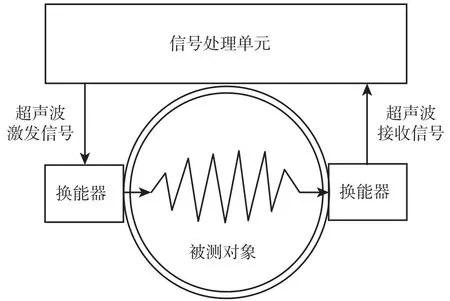
图5 超声波测量简化模型Fig.5 Simplified model of ultrasonic method

超声波流量计在实际应用中,由于被测时间包含了超声波信号在管壁材料中的传输时间、激励及接收点信号在电子部件及电缆中的传输时间、下位机计算单元的信号处理与计算时间等原因,从信号激励发出脉冲信号到接收器收到超声信号再到信号处理的被测时间包含时间延迟t0[5],因此公式(3)可变为公式(24)。

式中:Δti——第i条声道的渡越时间差;t0,i——第i条声道的时间延迟。

计算不确定度时,Δt与上下游实测时间相比足够小,因此可用第i条声道上的平均渡越时间ttr,i代替[5],则

时间项参数引入的不确定度主要可分为声波的传输时间、时间差与t0,因此可在零流量状态下,对时间项参数的时间差与t0的不确定度分量进行溯源。而针对复杂温度压力工况下的应用,可设计环境试验工装,同样在零流量下对声波传输的时间项参数进行验证。

4 结束语

从超声波流量计的测量原理出发,对测量不确定度进行了分析,根据各不确定度分量的性质及其产生原因,对时差法超声波流量计的单声道和多声道不确定度体系分别进行了划分评估。此外,从不确定度各分量的内容分解出发,对不同分量进行量化溯源,逐项分析出流量计测量精度在不同工况下所受到的影响,并对各不确定度分量的计算方法给出了评估建议。

结果表明,时间项引入的不确定度分量在不同工况下可进行区别评估;密度引入的不确定度分量评估在不同工况下没有方法上的区别;管体结构尺寸的变化可以分为制造因素及工况影响变形因素,可通过有限元仿真与加工精度控制水平计算得到;流速分布引入的不确定度分量须注意管段上下游安装环境,针对常用的积分方法通过实流标定或仿真分析来评估。综上,在现有流量标准装置条件下,采用不确定度分解溯源的方法,可最终建立主给水超声波流量计的不确定度计量溯源方法。