一种基于T型加减速的曲线拟合算法研究

刘志刚 黄刚鹏 张 旭 刘清建

（1.天津理工大学天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.天津理工大学机电工程国家级实验教学示范中心，天津 300384）

在复杂的曲面加工过程中，通常会根据各种约束条件将曲线段离散为微小线段，然后按照直线段进行速度规划，但如果要求拟合精度高，离散后的小线段往往存在计算量增多、加速度频繁变化等问题，从而影响加工效率[1-2]。

数控系统中速度规划的核心是加减速控制算法。国内学者针对速度控制算法进行了大量研究，但是这些算法并没有从本质上解决计算量大等问题。曲线拟合算法可以根据实际需求选择不同的曲线模型进行拟合。张等[3]提出了一种基于二次B 样条曲线的拟合及插补方法，该算法通过自适应的方法选取特征点，然后通过曲线拟合加工路径，避免了高次方程的求解。常见的曲线拟合算法在利用多项式进行拟合的过程中会产生大量方程，很难做到实时处理。

基于此，该文提出了一种基于T 型加减速的曲线拟合算法。该算法在一定程度上改善了上述缺陷，并且将拟合点的坐标计算为简单的二次方程，在保证加工精度的前提下，减少了计算量，可满足高速、高精的加工需求。

1 T 型速度规划参数求解

该节中介绍了传统的T 型加减速算法，然后根据其核心公式的变形求解出拟合坐标所需的速度规划参数。

1.1 T 型加减速算法介绍

T 型加减速的基本原理是在指定的时间内，先以最大加速度加速到达目标速度，然后以最大减速度减速停止。该算法可以确保设备在规定时间内平滑地从静止状态加速到目标速度，到达目标位置时平滑地停止。在T 型加减速中，速度的突变往往来源于加工路径的变化，加速度的突变体现在加速度的从无到有[4-5]。T 型加减速曲线分为加速阶段、匀速阶段和减速阶段，基本公式如公式（1）所示。

式中：vs（mm/s）是运动的初始速度；v（mm/s）是经过一段加速或减速阶段后的速度；a（mm/s2）是加速度；S（mm）是位移；t是任意时刻的运行时间。

1.2 求解速度规划参数

先对要加工的线段的距离进行求解，根据几何学中平面内任意2 个点间距离公式（2），可计算AB段和BC段的长度，如公式（2）所示。

式中：lAB为AB段的长度；lBC为BC段的长度；A（xA，yA）为首点坐标；C（xC，yC）为尾点坐标；B（xB，yB）为待拟合曲线在点A处的切线矢量和在点C处的切线矢量的交点坐标。其中，x、y为空间直角坐标系的2 个坐标轴，（xA，yA）为第一个分段点的坐标，（xC，yC）为第二个分段点的坐标。

AB段、BC段运动图示如图1、图2 所示。

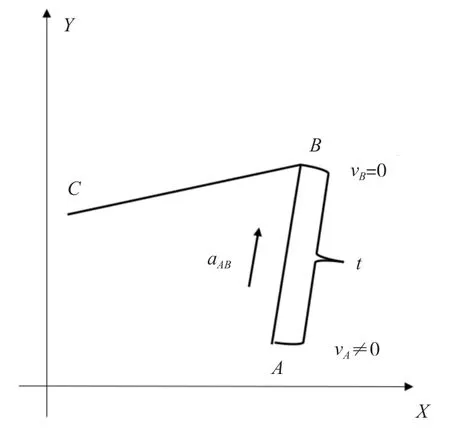
图1 AB 段运动图示

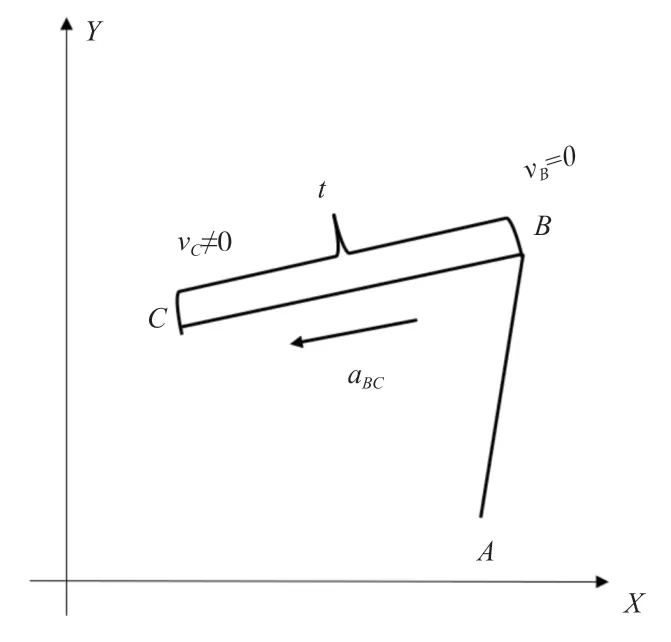
图2 BC 段运动图示

图1 中，在直线段AB上，从点A开始进行减速，直到点B时速度减为0，且A点的速度不能为0；图2 中，在直线段BC上，从点B开始进行加速，直到点C时速度最大，同样这里C点的速度也不能为0。在运行时间t时刻内，直线段AB与直线段BC上的运动是同时开始、同时结束的，即当在直线段AB上运动到点B时，在直线段BC上运动到点C（在T 型加减速中，加速阶段和减速度阶段的加速度大小相同，方向相反，即AB段的加速度aAB、BC段的加速度aBC大小相同，方向相反）。

根据匀变速直线运动规律公式（3）、公式（4），可以求得A点的速度、B点对应的速度，然后根据加速度的求解公式对AB段、BC段的加速度进行求解。这样就得到了T 型加减速的基础参数。

式中：SAB为t时刻运行的距离；lAB为AB段的长度，设定运行的距离为整段AB 段的长度；vA为A点的速度；aAB为直aAB线段AB的加速度。

式中：SBC为t时刻运行的距离；lBC为BC段的长度，设定运行的距离为整段BC段的长度；vC为C点的速度；aBC为直线段BC的加速度。

2 拟合点坐标求解

在上一节已经计算出SAB、vA、aAB、SBC、vC、aBC等参数，该节讨论拟合点坐标的求解。

2.1 求解速度矢量

根据平面内矢量的减法原则，可以计算直线段AB的矢量方向，如公式（5）所示。

式中：vf_AB为直线段AB的矢量方向；xA、yA分别为A点的横、纵坐标值；xB、yB分别为B点的横、纵坐标值；SAB为t时刻运行的距离；vf_AB_x为vf_AB在x轴方向的分量；vf_AB_y为vf_AB在y轴方向的分量。

矢量同时具有大小和方向，即矢量=矢量大小×矢量方向。根据公式（5）已经得到直线段AB的矢量方向，再根据公式（1）可求得t时刻的速度大小，即vt_AB=vA-aAB×t，最后根据已求出的直线段AB的矢量方向和速度大小，可以求解速度矢量，具体如公式（6）所示。

式中：为直线段AB上t时刻的速度矢量；vt_AB为直线段AB上t时刻的速度大小；vf_AB_x为已求出的直线段AB的矢量方向在x轴方向的分量；vf_AB_y为已求出的直线段AB的矢量方向在y轴方向的分量。

同理可求得直线段BC的速度矢量方向及大小，此时BC段t时刻的速度大小计算公式为vt_BC=vB+aBC×t。直线段BC的矢量方向求解公式如公式（7）所示，速度矢量求解公式如公式（8）所示。

式中：vf_Bc为直线段BC的矢量方向；xB、yB分别为B点的横、纵坐标值；xc、yc分别为C点的横、纵坐标值；SBC为t时刻运行的距离；vf_AB_x为vf_AB在x轴方向的分量；vf_AB_y为vf_AB在y轴方向的分量。

式中：为直线段BC上任意时刻t的速度矢量；vt_BC为直线段BC 上任意时刻t的速度；vf_BC_x为已求出的直线段BC的矢量方向在x轴方向的分量；vf_BC_y为已求出的直线段BC的矢量方向在y轴方向的分量。

速度矢量关系图如图3 所示。

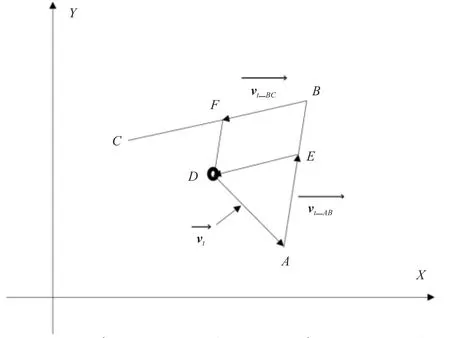
图3 速度矢量关系图

如图3 所示，四边形DEBF是平行四边形，根据几何关系可推得在矢量三角形ABC中，切线矢量即为合成速度矢量。根据图3 中的矢量三角形矢量的合成关系，可以推出速度矢量的求解公式，如公式（10）所示。

式中：是直线段AB上t时刻的速度矢量，是直线段BC 上t时刻的速度矢量；是合成速度矢量。

2.2 求解距离矢量St

首先利用公式（1）的变形对t时刻AB、BC这2 段距离矢量的大小进行求解，再结合2.1 节中求解出的速度矢量方向对距离矢量进行求解，距离矢量的求解方式和速度矢量的求解方式相似，如公式（10）、公式（11）所示。

式中：为经过t时刻在直线段AB上的距离矢量；vA为A点的速度；aAB为AB减速段的加速度；st_AB为AB直线段的距离矢量大小；vf_AB_x为已求出的直线段AB的矢量方向在x轴方向的分量；vf_AB_y为已求出的直线段AB的矢量方向在y轴方向的分量。

式中：为经过任意时刻t在直线段BC上的距离矢量；aAB为BC加速段的加速度；st_BC为BC直线段的距离矢量大小；vf_BC_x为已求出的直线段BC的矢量方向在x轴方向的分量；vf_BC_y为已求出的直线段BC的矢量方向在y轴方向的分量。

2.3 求解拟合点坐标

先求解合成的距离矢量。在2.2 节中已经求出直线段AB上的距离矢量和直线段BC上的距离矢量，根据公式（12）对距离矢量进行求解，Pt为拟合点，距离矢量即拟合点的坐标，由此可得拟合点坐标Pt=[xt，yt]。合成的距离矢量如公式（12）所示。

式中：是合成的距离矢量；是经过t时刻在直线段AB上的距离矢量；是经过t时刻在直线段BC上的距离矢量。

式中：xt为拟合点的横坐标；yt为拟合点的纵坐标；vf_AB_x为vf_AB在x轴方向分量；vf_AB_y为vf_AB在y轴方向分量；vf_BC_x为已求出的直线段BC的矢量方向在x轴方向的分量；vf_BC_y为已求出的直线段BC的矢量方向在y轴方向的分量。

将公式（13）展开可得公式（14）、公式（15）。

公式（14）、公式（15）中的各变量已经在之前计算中进行推导，均为已知变量。

根据公式（14）、公式（15）可知，该算法并没有出现高次方程，只是简单的二次方程计算，和其他曲线拟合方法相比，该算法更易于在数控系统上实现，能够减少数控系统的处理量并减轻计算负担。该算法也可以在加减速过程中实现更灵活和平滑的速度控制，提高数控系统的运动精度和平稳性，只需要通过调整拟合参数就可以提高加工的精度。

2.4 误差分析

设点A与点C的中点为点M，M点坐标为设首点与尾点之间的拟合曲线上时刻t/2 对应的坐标点为P2，将P2与中点M的距离作为拟合误差ε进行误差相关计算，计算过程不再展开，具体误差在第3 节仿真分析的结果中有所体现。

3 仿真分析

在数控系统中，通过输入待拟合曲线的参数，并根据设定的离散段数量N对待拟合曲线进行分段，可以得到各分段点的坐标及各分段点处的切线矢量，并在该基础上进行相关速度规划。为验证算法的正确性，对数控加工中常见的二次曲线椭圆弧和圆弧进行相关验证。

设定圆弧方程为x2+y2=r2，设初始3 个点的坐标为A2（0，0）、B2（1，1）、C2（0，1），运行时间t=10s。

采用MATLAB 软件进行验证，结果如图4、图5 所示。

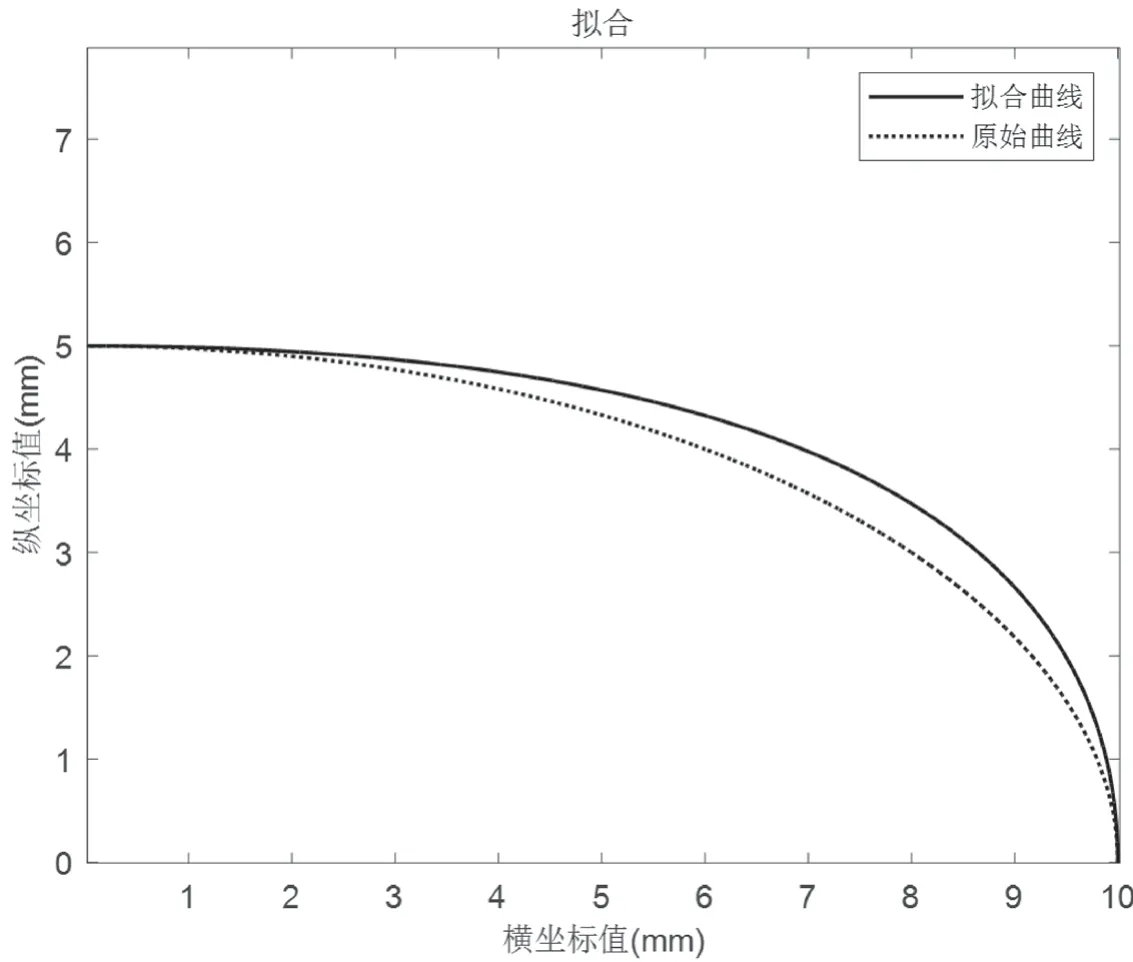
图4 椭圆拟合曲线图

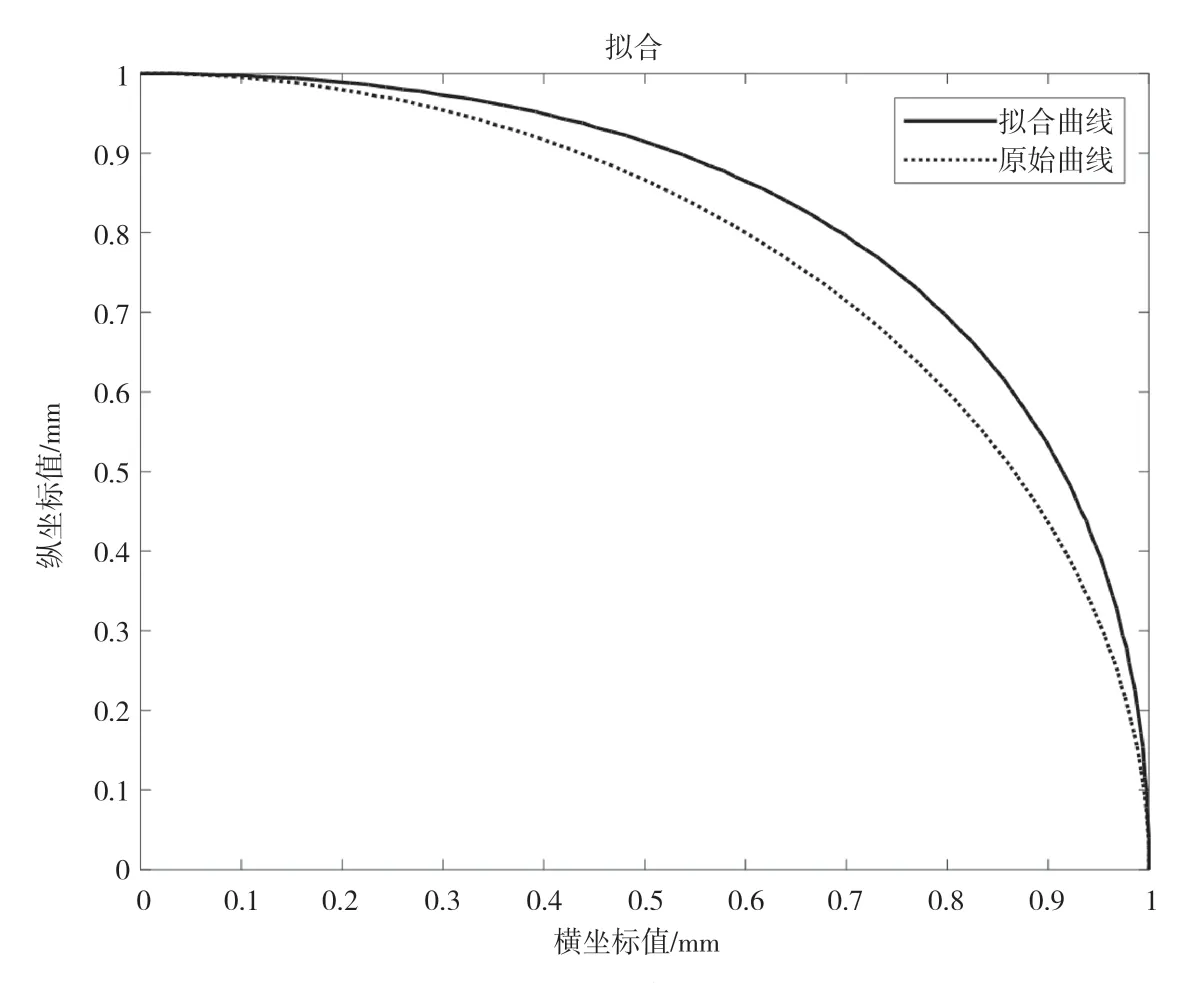
图5 椭圆拟合误差图

图4 和图5 是采用T 型加减速曲线拟合算法处理的椭圆弧拟合曲线图和圆弧拟合曲线图。由图4、图5 可知，生成的拟合曲线满足平滑度要求，并且接近加工路径，满足G1 连续的要求，比离散成小线段的路径更光滑，加工质量也更高，该算法后续也可以与实际的速度规划和插补结合，简化后续计算强度。

图6 和图7 是采用T 型加减速曲线拟合算法处理的误差图。由图5 可知，在椭圆拟合中，原始椭圆的弧长约为51.4mm，该算法很好地将拟合误差值控制在了0.4mm，误差百分比约为0.07%。由图6 可知，在圆弧拟合中，原始圆弧的弧长约为1.57mm，该算法很好地将拟合误差值控制在了0.06mm 内，误差百分比约为0.38%。并且2 种曲线的加工误差最大的地方基本也在T 型曲线的中点位置与被拟合曲线中点的距离，满足加工要求的同时降低了误差。

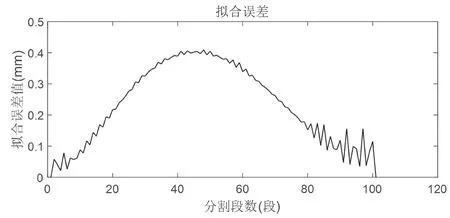
图6 圆弧拟合曲线图

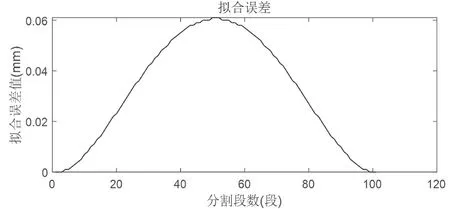
图7 圆弧拟合误差图

4 结语

该文针对传统的、基于多项式等的曲线拟合算法存在的计算冗长、复杂等问题，提出了一种基于T 型加减速的曲线拟合算法。该算法通过T 型加减速控制得到的相关参数对拟合点进行精准计算。该算法将拟合点坐标计算为简单的二次方程，满足了G1 连续的特性。通过试验验证，该算法能够在满足约束条件的情况下，较好地控制误差且整体运行简单。