基于多目标模型的钢板数控切割路径优化

王立志

（中煤北京煤矿机械有限责任公司，北京 102400）

数控加工在机械加工领域占有举足轻重的地位，可大幅度提升机械加工的效率和品质，成为当前机械加工行业的主流技术[1]。数控加工依托数控机床、数控加工中心等高端设备，以数控程序为加工工艺过程的控制核心，在配套夹具、刀具等的辅助作用下，以最佳效果完成机械加工任务[2]。可见，数控程序是数控加工提升效率和品质的关键所在。在钢板切割和加工过程中，要想提升加工效率、以更短的路径完成机械加工任务并节省更多的型材，关键在于对切割路径进行优化[3]。这个切割路径的优化过程受多方面条件、多个参数的影响，需要将这些参数纳入一个统一的模型，根据特定的目标限制完成优化处理。该文选用了多目标模型，用于钢板数控切割的路径优化。

1 钢板孔群加工案例分析

在数控加工的过程中，为了达到加工的高效率，一般需要对加工方法、加工工艺等进行合理的选择，最后形成最合理的加工路径。所谓合理的加工路径，一方面要确保加工精度要求，另一方面要尽可能减少加工路径的总长度，从而减少加工所用的时间。在满足上述2 个方面的基础上，尽可能减少损耗面积，确保剩余型材的整体完整性。

下面以一个孔群加工为具体的研究案例，对合理的加工路径进行分析。所谓孔群加工，就是在一块钢板上加工出多个孔，这些孔共同构成一个孔群。因为各个孔的位置、孔的内径和深度等要求均不同，就需要合理的加工路径。

一个具体的孔群加工案例如图1 所示。

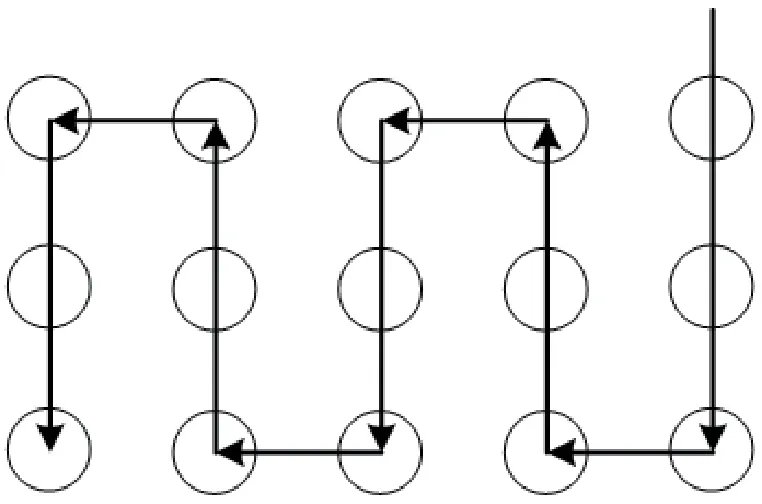
图1 垂直向走刀为主的加工路径

图1 中，钢板上要加工的孔群一共包括15 个孔，这里设置的是相对简单的情况，15 个孔的直径相同、深度相同，并且均匀排列。加工过程中，仅用一把同类型的刀具完成加工即可。如图1 所示，给出的是以垂直向走刀为主的加工路径，从最右侧切入后，先加工第一列的孔，然后进行水平转向，再挑头向上，加工第二列的孔，以此类推，从而完成全部5 列孔的加工。但是该加工过程中，刀具需要完成8 次转向，加工时间较长，并不是最优的。因此改为水平向走刀为主的加工路径，如图2 所示。

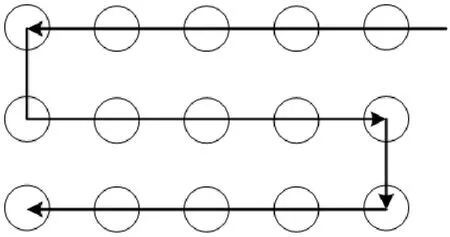
图2 水平向走刀为主的加工路径

如图2 所示，刀具以水平向走刀为主，先从最右侧切入，加工水平方向上第一排5 个孔，再转向下加工水平方向上第二排5 个孔，再转向下加工水平方向上第三排5 个孔。对比图1 和图2 可知，在该孔群加工任务中，水平向走刀为主的加工路径更优，刀具只需完成4 次转向即可。通过图1、图2 的比较可知，虽然孔群加工是非常简单的案例，但不同加工路径仍然会导致加工效率的明显不同。加工路径长的将会消耗更多的加工时间、加工效率低，而加工路径的延长也会增加风险概率。相反地，加工路径短的将会消耗更少的加工时间、加工效率高，而加工路径的缩短也会降低风险概率。

可见，在同一加工任务、相同的加工条件下，如果能够获得更短的加工路径，对加工过程是非常有利的。为此，就需要对基本的加工路径进行优化，该优化需要根据实际加工条件，配置各种必要的加工参数，进而采用合理的优化模型和优化方法，通过数学计算达到路径优化的最终目的，以期获得更短的加工路径并提高加工效率。

在实际加工任务中，关于类似任务究竟选择垂直向走刀为主的加工路径还是选择水平向走刀为主的加工路径，可以根据公式（1）来判断。

式中：i代表第i个停刀点位；n代表所有停刀点位的总数；xi代表第i个停刀点位的横坐标；xi+1代表第i+1 个停刀点位的横坐标；yi代表第i个停刀点位的纵坐标；yi+1代表第i+1 个停刀点位的纵坐标。

如果满足了公式（1）上面不等式的条件，则表明水平向走刀为主的加工路径更短，应选择X方向为主的加工路径；如果满足了下面不等式的条件，则表明垂直向走刀为主的加工路径更短，应选择Y方向为主的加工路径。

实际案例中的多孔孔群加工路径如图3 所示，该实际案例是包括多个孔的复杂孔群的加工路径规划结果。从图3 可以看出，孔的数量非常丰富，孔间距离也不相等，走刀路线无法实现全程的等距规则走刀。因此需要更好的优化方法来完成加工路径的优化。

图3 实际案例中的多孔孔群加工路径

2 多目标优化模型与切割路径优化

一次实际加工任务的完成过程中，最优加工方案的制定、最合理加工路径的选择都是根据多个目标的综合作用来制定的，其中决定加工效率和加工收益的就是加工时间和加工成本。加工成本和加工路径的长短直接相关。在同样的加工任务中，加工路径越短，加工成本越低。加工时间也同样与加工路径的长短有关，加工路径越短，加工时间也越少。可见，这2 个目标和加工路径之间的关系具有同向性。为此，以这2 个目标为对象构建多目标优化模型，以实现切割加工路径的优化。

首先，加工时间的综合计算模型如公式（2）所示。

式中：tw代表钢板切割加工中一次加工任务完成的总时间；tm代表钢板切割加工中完成一次加工任务所需的切削时间；to代表钢板切割加工中完成一次加工任务所需除了换刀以外的辅助时间；T代表刀具的可靠使用周期；代表钢板切割加工中完成一次加工任务所需的换刀次数；tc代表一次换刀所需的时间。

其次，加工成本的综合计算模型如公式（3）所示。

式中；C代表钢板切割加工中完成一次加工任务的总成本；M代表加工过程因时间产生的单位加工成本，元/min；tm代表钢板切割加工中完成一次加工任务所需的切削时间；to代表钢板切割加工中完成一次加工任务所需的除了换刀以外的辅助时间；T代表刀具的可靠使用周期；代表钢板切割加工中完成一次加工任务所需的换刀次数；tc代表一次换刀所需的时间；Ct代表刀具的使用成本，元。

再次，为了实现加工路径的优化，该文同时考虑加工时间和加工成本2 个参数，构建多目标优化函数，其数学模型如公式（4）所示。

式中：φ代表多目标优化的综合函数；k1代表以加工时间为目标的优化系数；k2代表以加工成本为目标的优化系数；tw代表钢板切割加工中完成一次加工任务的实际总时间；tn代表钢板切割加工中完成一次加工任务的未经优化的理论总时间；C代表钢板切割加工中完成一次加工任务的实际总成本；Cn代表了钢板切割加工中完成一次加工任务的未经优化的理论总成本。

最后，得到上述的优化模型后，在加工路径的优化过程中，综合考虑加工时间和加工成本参数，从而得到最合理的加工路径。

3 钢板数控加工的切割路径优化试验

上述以孔群加工为案例，分析了加工路径对加工效率的影响。进而从加工时间和加工成本出发构建了包括这2个目标的多目标优化模型。在接下来的工作中，该文以10组钢板切割的数控加工案例为研究对象，通过试验验证路径优化带来的效果。

在10 组钢板切割任务中，将多目标优化获取加工路径完成加工的时间和没有经过优化的加工时间进行对比，结果见表1。

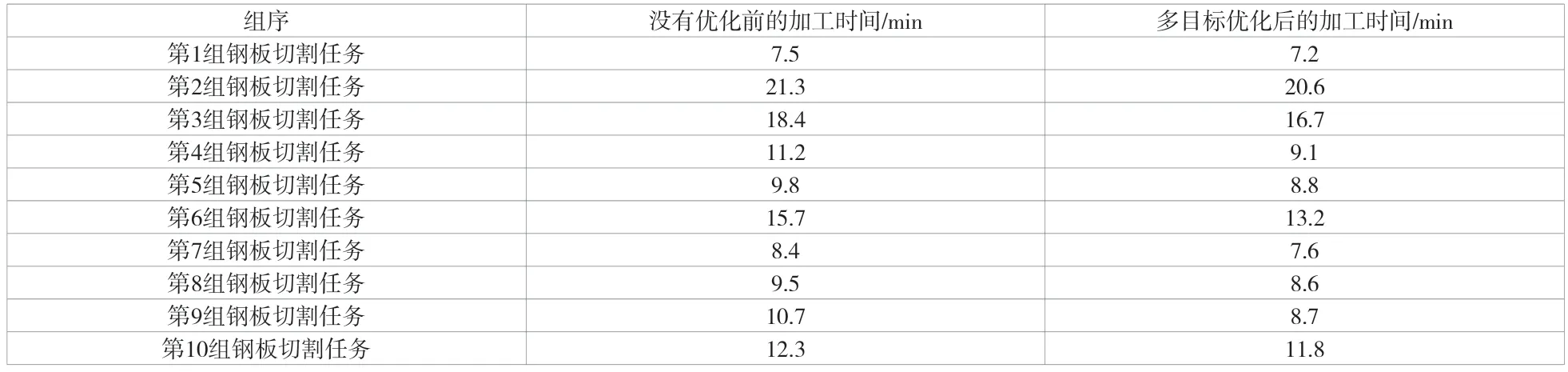
表1 钢板切割路径优化前、后的加工时间对比

表1 中，第一列数据代表钢板切割任务的组序，第二列数据代表切割加工方案未经加工优化所需的加工时间，第三列数据代表切割加工方案经过加工优化后所需的加工时间。从表1 的数据对比可知，第2 组钢板切割任务较复杂，用了21.3min；其次是第3 组钢板切割任务，用了18.4min；第1 组钢板切割任务最简单，用了7.5min。经过该文构建的多目标函数优化方法优化后，因为加工路径变短，所以优化后加工时间都有所减少。其中，第6 组钢板切割任务的用时从优化前的15.7min 减至优化后的13.2min，缩短了整整2.5min，加工效率大幅度提高。

为了进一步对表1 中的数据进行直观的展示，将其绘制成柱状图，结果如图4 所示。

图4 中，横坐标代表钢板切割任务的组序，第1 组到第10 组分别用01、02、……、10 表示，没有单位；纵坐标代表钢板切割任务所消耗的加工时间，单位是min。从图4 中的柱状图对比可以看出，经过多目标模型的优化后，10 组钢板切割任务的加工时间都有所减少，加工效率普遍得到了提升。相对而言，原本加工时间就较少的钢板切割任务，优化所减少的时间量也比较少。但这也不是唯一的因素，切割加工任务的复杂程度也会导致优化效果的不同。

图4 表1 中数据的柱状图结果

进一步观察执行优化加工后的钢板节约比率，如图5所示。

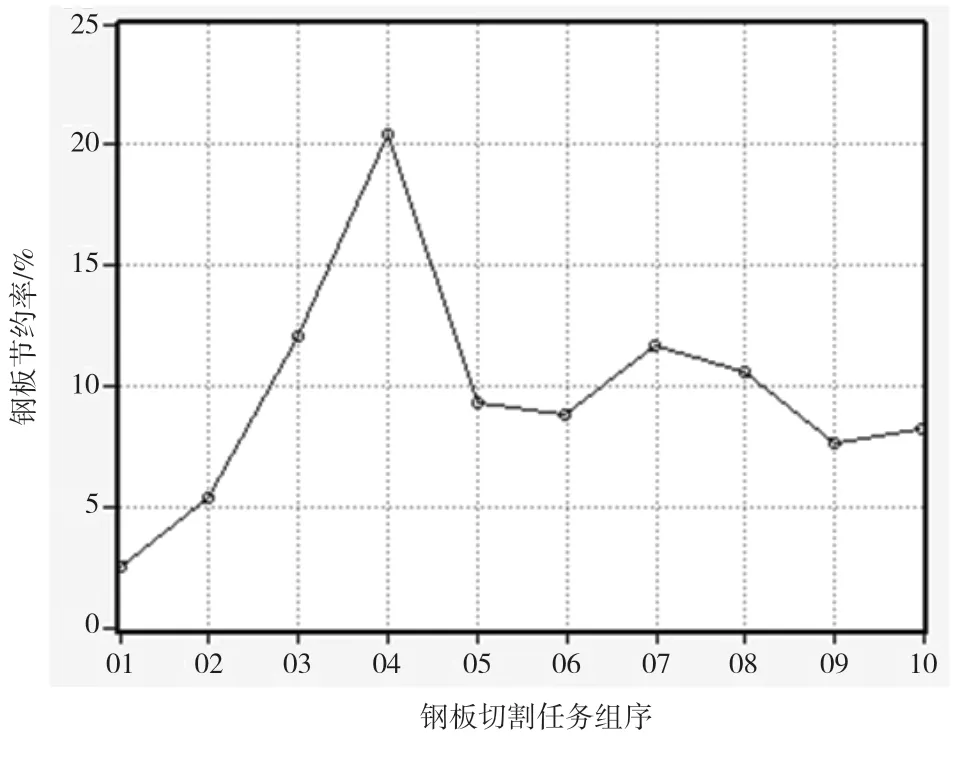
图5 钢板切割路径优化后的钢板节约率

图5 中，横坐标代表钢板切割任务的组序，第1 组到第10 组分别用01、02、……、10 表示，没有单位；纵坐标代表执行多目标优化以后钢板的节约率。从图5 的曲线情况可知，经过多目标模型的优化，10 组钢板切割任务均具有一定量的钢板节约率。其中，第4 组节约比率最高，超过了20%；第1 组节约的比率最低，低于5%。从平均节约程度来看，执行多目标模型的优化后，钢板节约率提升近10%，取得了较好的效果。

4 结论

数控加工日益成为机械加工的主流方式，不仅加工精度高，而且加工效率也较高。以钢板切割为例，数控加工可以通过优化加工路径来减少加工时间、节约加工成本。该文以孔群数控加工为例，分析了以X方向为主的加工路径和以Y方向加工为主的加工路径的区别。进一步，基于加工时间和加工成本2 个目标，构建了多目标优化函数。试验结果表明，在10 组钢板切割任务中，执行了多目标模型的优化方案后，10 组钢板切割任务的加工时间均明显减少、钢板节约率均有明显提升。