应用CAE结构仿真技术改进薄壁箱体承载能力的探究

杜建霞 李 琼 张红玉 周建军 王 宁

（甘肃机电职业技术学院，甘肃 天水 741000）

随着新知识、新技术在装备制造业迅速发展、应用，以计算机仿真技术为前提可以实现产品全数字化、无图纸虚拟设计，从而缩短产品开发周期、提高产品设计开发的一次成功率，进而应对瞬息万变的市场竞争需要。因此，当采用现代装备制造企业解决实际工程问题时，常常将以往复杂、耗时且耗资的手工计算或材料试验等交由CADCAE 等计算机辅助技术去完成。CAE 仿真技术因其具有直观、操作简单以及快捷便利等优点在技术改造、设计创新以及新学科专业培训教学中得到快速发展。因此，作为新时代的机械行业技术人员，掌握用CAE 仿真技术对分析和解决实际工程问题具有重要意义。该文应用CAE 结构仿真技术改进薄壁箱体承载能力，以C-GIS 箱体为例，探究如何运用CAE 结构仿真技术线弹性静力学分析方法改进薄壁箱体承载能力的方法。

1 C-GIS 薄壁箱体

C-GIS 箱体是由厚度为2.5 mm～3.0 mm 的6 块不锈钢板材组成的密封的薄壁外壳，将所有高压部件完全密封在充满一定压力的绝缘气体SF6气箱内，才可以适应大温差、高海拔、沙漠、粉尘、震动以及腐蚀性等极其恶劣的环境。

薄壁零件因其受力、受热极易变形这一特点，一定程度上制约其发展。改善C-GIS 箱体的承载能力将对提高中压柜质量有重大意义。C-GIS 箱体由6 块不锈钢薄壁面板焊接而成，因此，研究人员往往将提高箱体承载强度转化为对6 块面板的承载能力研究，一般采用冲压折弯板材或增加加强筋等措施来提高其承载能力。在C-GIS 箱体6 块面板中，因为密封面板作为封装高压部件的一面，开口较大，所以其强度受影响也最大，如果用传统的制造工艺增加其强度，就需要经过设计—试制—调试—再试制等步骤，不但耗时，而且成本高，无法适应瞬息变化的市场需求。

2 CAE 仿真技术简介

CAE 结构仿真技术是一款采用有限元方法对零部件产品结构与热相关领域进行仿真分析的软件，可方便快速进行几何建模、模型修复、网格划分以及边界条件设置等前处理工作，求解完成后，可以利用丰富的后处理功能查看仿真结果并进行对比分析，从而得出需要的运算结果。CAE 仿真技术通过建造任何零部件虚拟化几何模型，在设计其精准的数据样本后，应用弹性静力分析法构建零部件在不同工况下的变形-应力-应变分布状况，从而得出其承载能力以及应对措施，从根本上改变了传统机械设计制造的弊端，不仅可以降低成本，而且还可以提高效率。

3 CAE 仿真技术线弹性静力分析法的应用条件

3.1 线弹性静力分析法

3.1.1 线性弹性体

当一个物体所受荷载不超过某一限值（弹性极限）时，其所受荷载与变形呈线性关系（即材料遵从胡克定律），如果去除外加载荷后，物体没有残余变形的物体就称为线性弹性体，又称线弹性体[1]。

3.1.2 线弹性静力学分析

线弹性静力学分析是分析当载荷应用于物体时物体发生变形，载荷作用到整个物体上，研究外部载荷引起的物体的内力和反作用力使物体达到新的静力平衡状态的情况，属于力学分析方法[1]。

3.2 应用线弹性静力分析法的3个条件

CAE 仿真技术线弹性静力分析法将弹性力学中通过构建平衡方程、几何方程以及物理方程（本构方程）三类偏微分方程组等基本方程来描述物体在外载荷作用下的变形-应力-应变关系，大量高难度分析运算交给计算机完成[2]。但是试验体必须满足以下3 个条件：1） 线弹性静力学分析是利用仿真软件计算线弹性体在静载荷作用条件下物体所产生的位移，也就是物体的变形（及由此所产生的应力和应变）。2） 研究对象加载的是静载荷而非动载荷。3） 研究的物体材料为线弹性体。

4 任务分析

4.1 箱体的受力及试验条件分析

4.1.1 建立受力模型

在实际工程案例分析中，为了便于分析计算，将一些机构简化为一个力学模型，例如飞机的机翼、传力的轮齿以及塔吊等均可简化为悬臂梁，对其在载荷作用下的强度、刚度和稳定性进行计算，可以简化设计难度，降低试验成本。根据该文研究对象C-GIS 箱体薄壁面板的受力状态也可以简化为悬臂梁模型进行研究，并不影响对提高其承载强度的研究思路。

4.1.2 试验条件分析

首先，仿真材料为304 不锈钢，属于金属弹性材料范围，符合胡克定律条件；材料属性中弹性模量E、密度ρ以及泊松比v与线弹性静力分析的仿真结果计算有统计学意义，屈服强度σs可作为仿真运算结果是否在弹性范围范围之内的对比验证条件。其次，薄壁面板的细长比远大于10，仿真时设置的边界条件对薄壁面板挠度分布的影响很小，仿真结果将更逼真、更接近生产实际需要。最后，通过改变薄壁面板的预定载荷或结构，分析对比薄壁面板的变形和应力变化等，从而得出试验结果。

4.2 网格划分

网格划分是CAE 仿真的首要工作，其本质是利用有限个离散的单元体来代替连续的计算域。结构仿真过程中对模型的网格化处理决定仿真结果的准确性。根据有限元离散原理，网格划分数量和细化程度是减小假扩散的措施之一，决定计算精确度，也就是说网格的精度越精细致密，仿真的效果会越逼真，同时也会导致计算量增加，从而影响计算速度。因此，划分网格时既要保证仿真效果，也要兼顾计算速度。

4.3 仿真试验及强度分析对比

C-GIS 箱体是由6 块薄壁面板组成的，箱体的承载能力是由6 块面板的承载能力决定的。为了兼顾6 块面板的承载强度，该试验选择开口比较大的密封面板作为试验对象进行仿真试验。

4.3.1 密封面板的不加加强筋与增加加强筋的仿真试验对比

密封面板的材料为弹性模量E=2.0×1011P 、密度ρ=7.85×103kg/m3、泊松比v=0.32 且屈服强度σs=250 MPa 的线弹性材料。网格类型选择四面体、高阶。将密封面板的承载试验简化为悬臂梁进行仿真试验，密封面板的一端为固定端，加载自重G；另一端为自由端，加载F=10 N 的集中载荷。图1 为未加加强筋的密封面板位移云图，图2 为两侧各加2 条加强筋的密封面板的位移云图。在相同的工况情况下，未加加强筋的密封面板的最大位移量为23.8 mm，如图1 所示；两侧各加2 条加强筋的密封面板的最大位移量为0.289 9 mm，如图2 所示。增加加强筋后密封面板的最大变形量减小了80 多倍。但是由图2 可知，在密封面板的右侧添加集中载荷F的一侧，出现了面板上变形量最大位置，结合密封面板的实际生产要求，可以在对加强筋的数量、疏密以及方向等进行调整后，再次进行仿真试验，如图3 所示，在密封面板的开口四侧各增加1条加强筋，加载同样载荷后的位移云图。由图3 可知，密封面板的最大位移量为0.925 7 mm，与图2 两侧加2 条加强筋的位移云图相比变形量差约为0.6 mm，但是整个密封面板避免了局部塌陷式变形量较大的情况，图3 更符合实际生产需要。

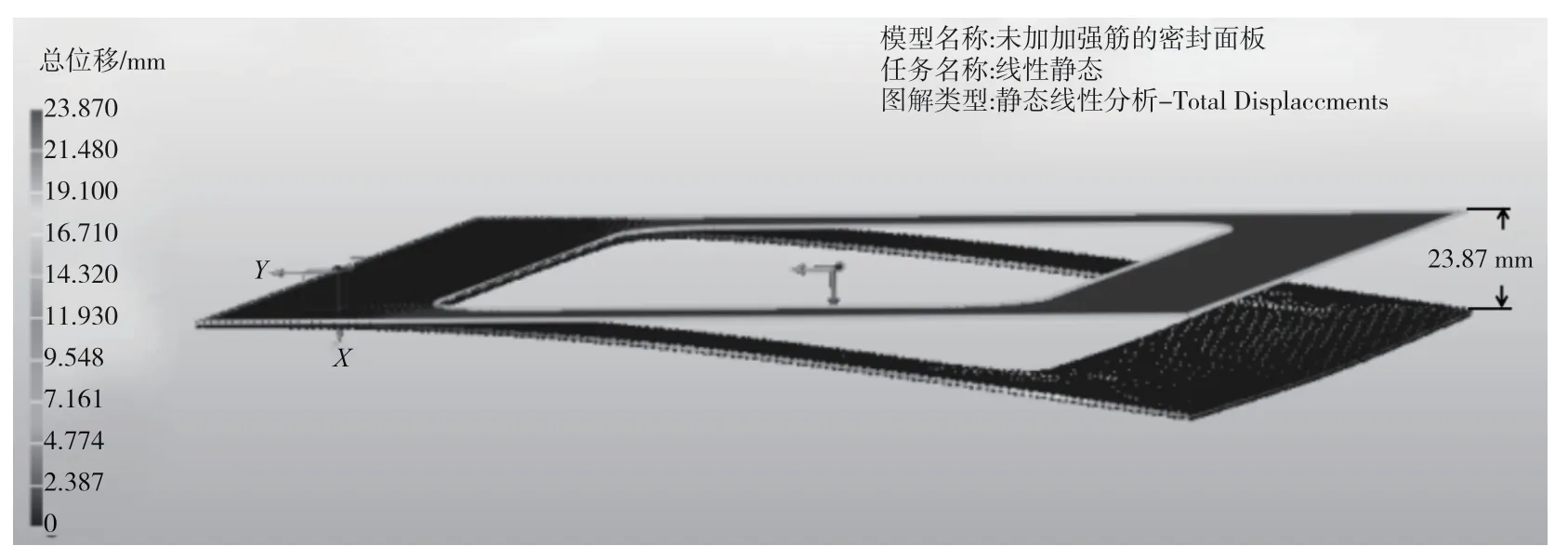
图1 未加加强筋的密封面板的位移云图

图2 两侧加2 条加强筋的密封面板的位移云图

图3 增加加强筋的密封面板的位移云图

4.3.2 加强筋的承载方向与承载能力对比

构建加强筋模型及网格化处理，通过CAE 软件构建长H×宽a×高b=300mm×8mm×12mm 的实心长方体加强筋模型。为了方便建模及后续对仿真结果分析对比方便，将梁的横截面高度b、宽度a和长度H与CAE 软件坐标系中的x轴、y轴和z轴一一对应。为了增加仿真试验的质量和逼真性，减少后续网格化的数量，建模时尽量避免对梁进行倒角倒圆等特征处理。材料依然选择线弹性材料，结合加强筋的承载及结构复杂程度选择其网格信息见表1，可以保证仿真结果的真实性。

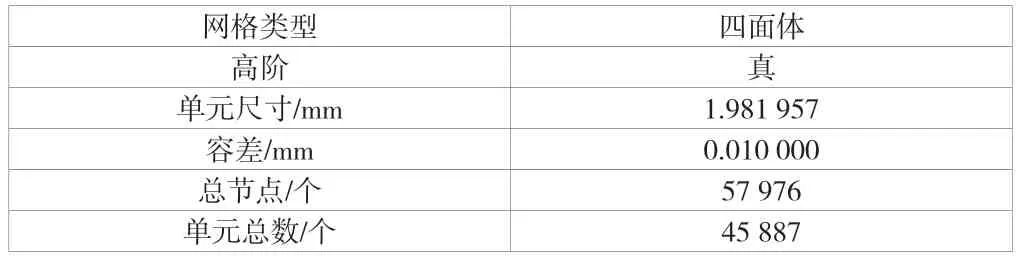
表1 加强筋的网格信息表

图4（a）为平放加载，即沿y轴方向加载集中载荷F和重力G，图4（b）为加强筋竖放加载，即沿x轴方向加载集中载荷F和重力G。根据仿真位移云图-应力云图-应变能云图得出试验数据，见表2。

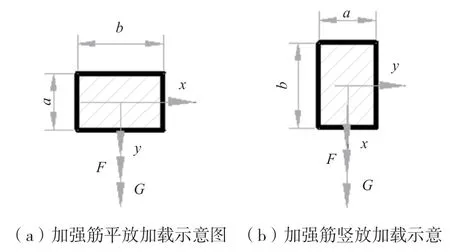
图4 加强筋平放加载和竖放加载示意图

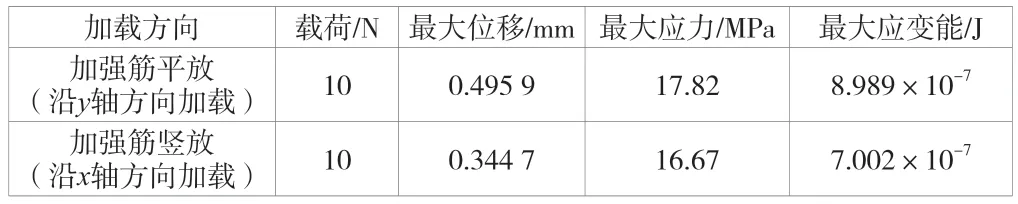
表2 加强筋平放与加强筋竖放加载仿真试验数据表

由表2 可知，加强筋竖放加载比加强筋平放加载产生的最大位移值、最大应力值以及最大应变能小，加强筋的承载能力提升约1 倍。试验结果表明，在不改变加强筋形状、结构以及质量的前提下，只改变加强筋的承载方向，就可以提高薄壁面板的承载能力。

另外，当加强筋的最大应力值等于屈服强度σs时，其最大载荷Fmax≈149.97N。当给加强筋施加最大载荷Fmax，加强筋离散分离时的信息与表1 相同，加强筋横、竖放时的最大位移、应力以及应变能见表3。

表3 加强筋横放、竖放时Fmax 的位移、应力、应变能对比表

由表3 可知，当同一根加强筋为竖放状态时，承受最大载荷时所产生的最大位移、最大应力及最大应变能均小于加强筋横放状态。因此，在同等材料、结构情况下，通过改变加强筋的承载方向不但可以提升承载能力，而且还可以达到节省材料的目的。

5 结语

应用CAE 仿真软件对C-GIS 薄壁箱体的密封面板加强筋的结构位置、疏密数量以及改变加载方向进行仿真试验，可以快速模拟与生产实际情况更接近的试验数据。CAE 仿真技术与生产实际结合就可以将晦涩难懂的偏微分方程组运算交由计算机完成，降低了设计创新及试制成本，让模拟更复杂的零部件工况仿真试验成为可能。

综上所述，可以利用CAE 结构仿真技术提前对零部件的结构、材料以及载荷等进行调整或改进，从而提高设计速度、缩短试验周期以及提高产品设计开发的一次成功率。结构仿真软件因其强大的运算功能和方便、快捷且直观的造型将成为机械零部件最常用的设计改造软件，在节省材料、零部件结构改造设计领域大有可为，可以广泛应用于科研院所研究、职业院校专业人才培养及企业技术改造等领域。