利用近场动力学理论对高分子材料相变分析
2023-09-07郭一谚姜玉海白丽红武海玲王晓丹
郭一谚 姜玉海 白丽红 武海玲 王晓丹
(1.中国兵器集团第五二研究所烟台事业部,山东 烟台 264003;2.沈阳地区驻包头第一军代室,内蒙古 包头 014033)
在抗高速冲击的过程中,多层纤维叠铺的层结构能够最大限度地利用纤维韧性吸能和约束特性,避免应力集中,加快纤维对冲击力的响应速度。但是叠铺层结构的层与层之间容易发生滑移现象,通常采用胶黏剂复合材料就可以保证复合材料的完整性,提高纤维复合材料的整体力学强度。纤维复合过程中使用的胶黏剂作为高分子材料中的成员,在去除所有材料中总的范德华力作用前,其化学键早已断裂,因此高分子材料没有气态,只具有液态和固态形式。作为复合工艺的必要材料,相变的变化趋势是其附着力、使用寿命及老化时间需要考虑的重要因素。
1 近场动力学的热扩散理论
当高分子材料内颗粒的运动状态处于稳定状态时,颗粒的运动势能小于范德华力的能量和,如果颗粒间的相互碰撞运动能够引起内部的热力变化,就会破坏内部的能量平衡,形成热流量。随着分子运动,材料内部的热能扩散,单位时间t通过单位面积的热流量被称为热通量(如图1所示)。热通量可以衡量高分子材料内部的热能的扩散和水分子吸收、逸失的情况——水分子含量变化,材料内部的黏度随之变化,促使材料产生相变(由液态趋于固态,直至固化或逆向变化)。此外,还会影响水分子和晶格的缔合度,缔合度的变化对固化的高分子材料聚合物与其他材料的结合度有统计学意义[1-3]。
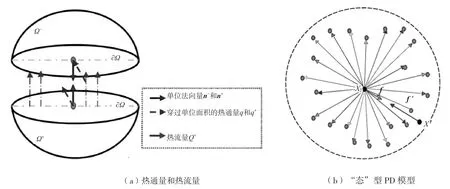
图1 热扩散模式与“态”型PD 模型
在近场动力学中,热流(标量)状态h(x(i),t)包括与质点x(i)相关的所有相互作用的热流密度(i=1,2,…)(t为时间),可以用n维数组表示,如公式(1)所示[4-6]。
式中:h(x(k),t)为以H(k)(j)为n维的热流密度;h(x(j),t)为以H(j)(k)为n维的热流密度。
2 个n维热流密度H(k)(j)≠H(j)(k),如公式(2)所示。
式中:x(j)、x(k)为2 个质点(j或k=1,2,…)。
其中,(x,t)〈x′-x〉的量纲为热流量除以体积(单位时间、单位体积的热量),因此PD 的热流量可以与热通量q联系起来(如图1(a)所示)。
每个质点x(i)都有一个热势,微热势z(i)(j)取决于质点x(i)和与其发生相互作用的所有质点之间的温度,与x(i)和x(j)之间的热能交换相关,因此微热势z(i)(j)≠z(j)(i),如公式(3)所示。
式中:Θ(j)为质点x(i)的温度;Θ(j)为质点x(j)的温度;Θ(ni)为与质点x(i)相互作用的第n质点的温度(n=1,2,3,…)。
在计算过程中,定义温度(标量)状态ι如公式(4)所示。
式中:x′为质点x在时间t发生变化∆t瞬间后的质点;Θ(x,t)或Θ(x′,t)为t时刻质点x或x′的温度。
由公式(4)可知,微热势z(i)(j)可以写成温度状态的函数=(ι),根据微势能的函数形式,热流状态h可以写成温度状态的函数=(ι)。在微观状态下,高分子材料的热传导源于晶格振动形式的分子运动,在近场动力学态型的热扩散的理论分析中,Hx 邻域内以质点X为中心,分析半径δ的子域内的质点xi′(i=1,2,…,n)与x的相互作用的位移和力矢量的变化可以模拟高分子材料的分子与晶格的结合度的变化趋势,得出材料相变对材料附着力的影响。StewartSilling 博士构建的“态”基PD 模型(如图1(b)所示)可以描述高分子材料内部的分子运动、热传导过程,根据公式(1)~公式(4)以及推导形式可以得出“态”型PD 热扩散运动方程的瞬态形式,如公式(5)所示。
式中:ρ为密度;为温度梯度;cv为比热容;Vx′为质点x′的体积;hs(x,t)为热源密度,且hs(x,t)=ρsb(x,t)(ρsb(x,t)为热源密度函数)。
这是关于时间(微分)和空间区域(积分)的积分--微分方程,不包括温度的空间导数求解,因此在不连续的地方不存在奇异性[5-6]。
2 PD 热扩散方程在高分子材料相变分析中的应用
2.1 利用PD 热扩散瞬态模型分析
当高分子材料从液态向固态转换时,会经历分子聚合、成膜到玻璃化的演变过程(图2 分析了高分子材料相变趋势)。
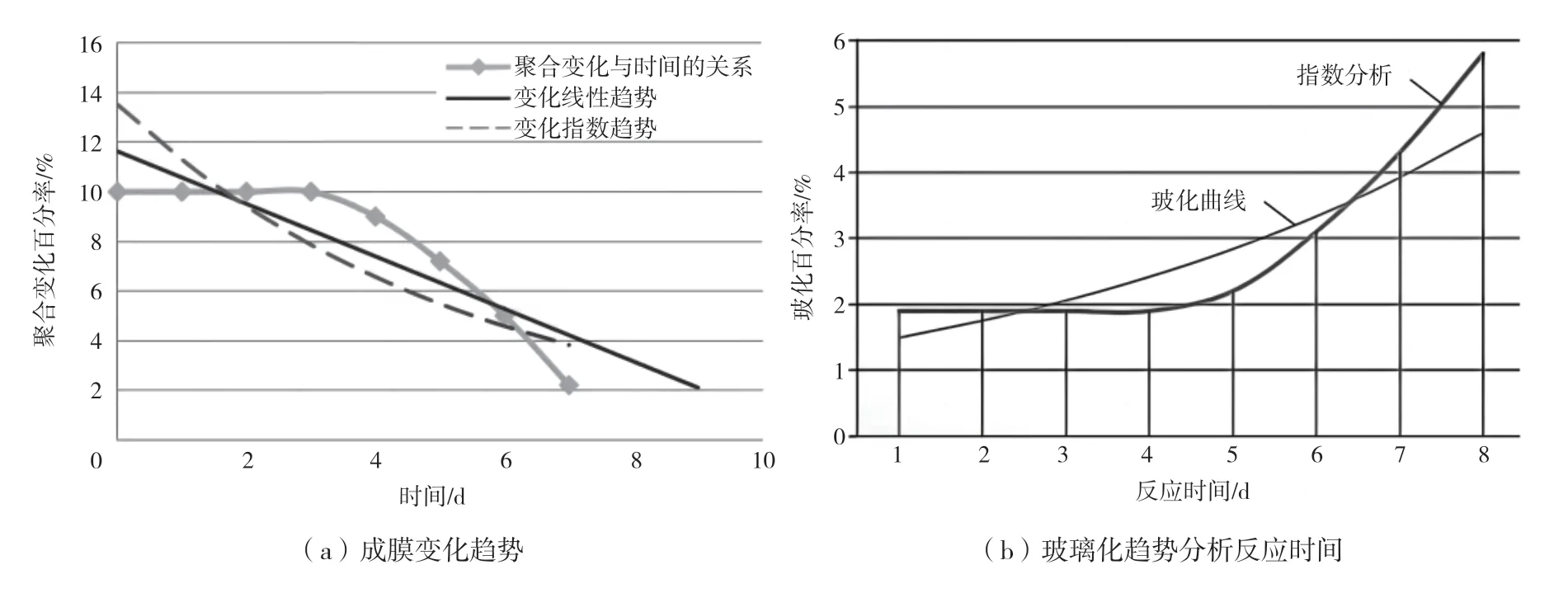
图2 相变趋势图
外部温度变化以及高分子材料内的热扩散导致的热势能的变化会影响材料相变的速率,相变过程的经验Fox公式(玻璃化温度计算)[7-8]如公式(6)所示。
式中:Tg为玻璃化的温度;Wi为第i组合在自由聚合物组成中所占的质量分数;ti为第i组合的聚合物玻璃化的温度。
需要注意以下3 点:1) Hoy 曾提出玻化速度MFT与效果的关系(K为成膜温度换算系数)。2) 成膜温度换算系数K一般为0.92~0.98。3) 某些情况下MFT可能略低于Tg,也可能略高于Tg,一般比较接近。
除了考虑固化过程(如公式(6)所示)涉及的因素,在解析PD 热扩散瞬态运动方程前,还要考虑瞬态形式下,材料玻璃化过程中存在独自状态的液态和固态区域(当材料逆向转换时也存在),这2 个区域有各自的未知温度场T1(x1,t)和T2(x1,t)。它们与必要的参数——未知的界面位置s(t)的逻辑关系如公式(7)、公式(8)所示[7-9]。
式中:α1和α2分别为液态和固态区域的热扩散系数;t为时间变量;x1、x2为2 个质点。
当T(s(t),t)=Tliquid(T(s(t),t)为t时刻x所处界面位置的温度;Tliquid为液态温度)时,为了求解温度分布和界面位置,∂T(s(t),t)对x1求偏导的方法存在需要施加的界面条件,如公式(9)所示。
式中:ρ为密度;hL为潜热,是改变单位质量物质状态可能需要的能量;s(t)为t时刻x的界面位置;κ1、κ2分别为液态和固态区域各自的导热系数。
高分子材料的热扩散是个瞬态过程,温度不是一个定值:不同区域、不同时间实际存在条件(例如环境温度、高分子材料所含自由基数量等)都会影响温度T,因此在程序中可以使用数维组表达。
2.2 并行计算解析热扩散瞬态运动
利用多处理器的并行计算方式解析PD 热扩散瞬态运动方程,求和公式比求积分的解更便于计算,因此需要利用质点领域内的求和转换为积分的形式,如公式(10)所示。
式中:V(j)为质点xj的体积;Vx为质点的体积。
将“态”型PD 热扩散瞬态运动方程转换成求和公式,公式(5)就可以转化为公式(11)。
式中:Z(i)(k)、Z(i)(k)为2 个热势能;V(i)为质点x(i)的体积;Θ(i)为点x(i)的温度;Θ(ni)为与点x(i)相互作用的第n质点的温度(n=1,2,3,…);Θ(j)为点x(j)的温度;cv为比热容;Θ(x,t)为温度梯度。
利用“态”型PD 热扩散瞬态运动方程拟合高分子材料的玻璃化转变率趋势和附着力的寿命,变量较多且计算数据量大。提高计算效率需要充分利用当前的计算处理设施的并行计算方法,关键需要考虑并行计算的载荷平均分配:将计算域分割成多个子域,通过控制集中度的变化和计算数据量分配处理器,从而充分发挥并行计算的最大优势,进而提高计算效率。
相变过程的特征是存在相分离界面移动,它们的数学模型是非线性的,并且难以获得精确解。在数值解析的过程中,可以利用质点x(i)处的PD 热扩散方程的离散格式,如公式(12)所示[10]。
式中:为热响应函数;=ρsv(x,t)为热源密度函数;Vj为质点xj的体积。
同时,运行计算时可以通过设置步长,在尽可能获得精确解析的情况下,也要考虑计算运行的效率,步长计数的源代码如下。

高分子材料的热扩散过程是瞬时变化,当时间t经过瞬时时间∆t后温度的变化,程序中通常用数维组表达一定条件内的变量,用来控制温度数组维数的通用源代码码如下。

因此,在t+∆t的时间内高分子材料相变的过程中,两态交接的界面随着材料不同形态的比例变化而产生位移变化的运动轨迹,通过解析据PD 热扩散瞬态运动方程得出描述曲线,如图3 所示。
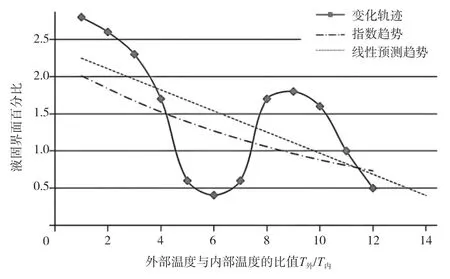
图3 界面随温度的变化
微观世界的分子之间的不平衡冲撞不断推动相变界面的位置移动,形成高分子材料相变的扩散轨迹。如图3所示,无论指数分析还是线性的预测都表示高分子材料在相变过程中液态和固态比例的变化趋势。在热扩散的过程中,高分子材料的液态和固态的交接处形成液固(或固液)界面的比例是变化的,瞬间变化x(i)的界面位置在t+∆t时刻如公式(13)所示[10]。
式中:S为∆x1中液相的比例。
3 结语
复合过程易导致材料间产生孔隙,而孔隙率与防冲击的性能成反比(孔隙率越高,防冲击的性能越低),为了研究胶黏剂的复合工艺过程和使用寿命与温度、压力的关系,该文应用“态”型的PD 瞬态热扩散理论,从微观角度分析了高分子材料相变过程是由不停地做无规律的运动的分子组成(分子间不断地随机撞击形成水分子的逸散或吸收、自由基组成的链的扩大或断开以及相变界面的形成)。因此,该文得出以下5 个结论:1) “态”型PD 模型相互作用的2 对质点之间的力矢量更适合描述2 个分子之间的斥力和引力形成的相互作用力,可以拟合分析高分子材料热扩散的运动曲线。2) 应用PD 模型求解积分,以分析高分子材料相变过程中质点位移和力矢量的变化以及对界面位移的影响,不存在运动过程中力矢量断开无从计算的奇异性问题。3) PD 热扩散瞬态模型主要描述∆t变化时间内质点的运动轨迹,适合分析高分子材料相变过程的瞬间微观变化,描绘高分子材料相变过程的线性预测趋势和指数趋势。4) 热扩散对高分子材料相变过程和水分子含量的影响是其与其他材料界面的附着力的主要因素之一,针对不同类型高分子材料的胶黏剂与参数不同的材料界面的复合的预测趋势分析,可以进一步从理论上分析热、压的加工工艺对高分子材料的生命周期、降低孔隙率以及层间界面更好结合的影响。5) PD 模型非常适合进行并行计算,通过分割子域的方法控制在不同区域配置点的集中程度,从而提高运算速度。
