级配分析中堆叠颗粒完整形态预测方法

蔡可天，王 建，夏万求，彭泽豹

(1.河海大学水利水电学院，江苏 南京 210024；2.浙江宁海抽水蓄能有限公司，浙江 宁海 315600)

0 引 言

级配是骨料各级粒径之间的分布情况，在堆石坝等工程中，土石料的级配影响坝体的抗压、抗滑和防渗等性能[1-2]，直接影响着工程施工质量[3-4]。目前，级配研究涵盖了水利[5]、公路[6]、矿业[7]等领域，准确地检测骨料级配一直是国内外学者的重点研究内容。

数字图像处理是一种非破坏性、非侵入性技术，包括岩石岩性分类[8-9]、边坡稳定性分析[10]、材料细观损伤性质[11-12]等，在工程中的应用非常广泛；同时，应用图像处理技术可在骨料开采、工程施工、质量检测全过程进行级配检测，是各行业中的热点研究内容之一。当前，针对级配的研究重点集中在目标颗粒分割和边缘识别方面[13-17]，并已经取得一定成果，但在实际应用中，由于被检测颗粒常处于堆叠状态，其中大部分颗粒存在一定程度的遮挡，即使能够完整提取颗粒边界也没办法准确测量颗粒面积和等效粒径，致使级配检测结果精度降低，因此补全不完整颗粒的边缘形态，恢复完整的颗粒形状，提高堆叠状态下颗粒的级配检测精度成为提高工程施工质量的必要。

本文提出了一种基于统计学信息的多阶段颗粒边缘快速预测方法，尝试根据可见的颗粒边缘补全完整颗粒，研究预测结果与颗粒真实状态的匹配度。

1 堆叠颗粒完整形态预测原理

对不完整颗粒边缘进行补全，需要从已知的颗粒边缘中提取最具备指导性的信息，辅助预测被遮挡区域的颗粒形状，由此提出基于真实颗粒边缘统计信息的多阶段颗粒边缘预测方法，不完整边缘预测过程如图1所示。通过分析边缘点位与边缘形态一致性和最小预测角度之间的内在联系，在边缘预测的不同阶段，选择相应参数，预测颗粒边缘走向。

图1 不完整边缘预测

1.1 颗粒形态影响参数

一个形状较规整的颗粒形态，如图1b所示，由平滑段和变化点依次组成，变化点之间属于平滑段，平滑段之间由变化点连接。因此，提出2个颗粒形态影响参数——方向一致角和最小预测角——用于表征边缘平滑段和变化点形态。

颗粒边缘以像素点为分析对象，点和点之间的位置关系如图2a所示，每个像素点邻域内存在共计8个相邻像素点，因位置关系，邻域内相邻点位与中心点之间夹角相差45°。定义不完整颗粒边界点分别为起点和终点，如图2b所示，选择起点为当前点，定义候选点为当前点邻域内像素点(不包括边缘像素点)，定义基准向量为当前点-终点向量、预测向量为当前点-预测点向量，定义预测角度θ为预测向量和基准向量夹角。颗粒边缘补全过程即在候选点中选出预测点，再以预测点为当前点，循环至起点-终点相连。

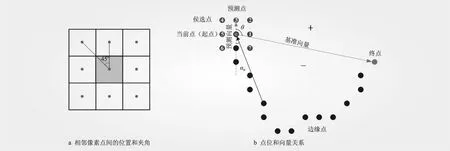
图2 颗粒边缘分析对象和影响参数

1.1.1 方向一致性

边缘形态的方向一致性用于衡量预测颗粒形态与前段颗粒形态的一致性，是影响颗粒形态走向的重要参数，采用边缘前n点和当前点之间向量与预测向量之间的夹角αn衡量，如图2b所示，n的取值与图像像素值相关。

1.1.2 预测角度

在候选点中选择不同预测点时，预测角度θ相应改变，如图2b所示，将位于基准向量正方向(相对于颗粒边缘)且预测角度最小的点定义为1位点，依次定义候选点为2～7位点，其中，1位点对应最小预测角θmin。不同点位的选择能够影响颗粒边缘形态走势变化，以最小预测角度为标准进行候选点选择，实现颗粒边缘形态变化。

1.2 多阶段颗粒边缘预测方法

多阶段颗粒边缘预测方法基本思想是对不完整颗粒边缘进行阶段式方向一致性生长和阶段式最小预测角度概率生长，多阶段交替补全完整颗粒，如图3所示。随着颗粒的补全进程，每阶段的最大预测点数呈下降趋势。方向一致性标准：选择候选点位中与方向一致角标准值αsta偏差最小的点，即和原本边缘形态一致性最高的点位，其中，方向一致角标准值αsta根据目标颗粒形态获取，当颗粒边缘形态较为平滑时，αsta取值较小。最小预测角度概率标准：基于最小预测角度-点位选择概率函数关系(统计数据获取)，选择概率最高点位。计算公式分别为

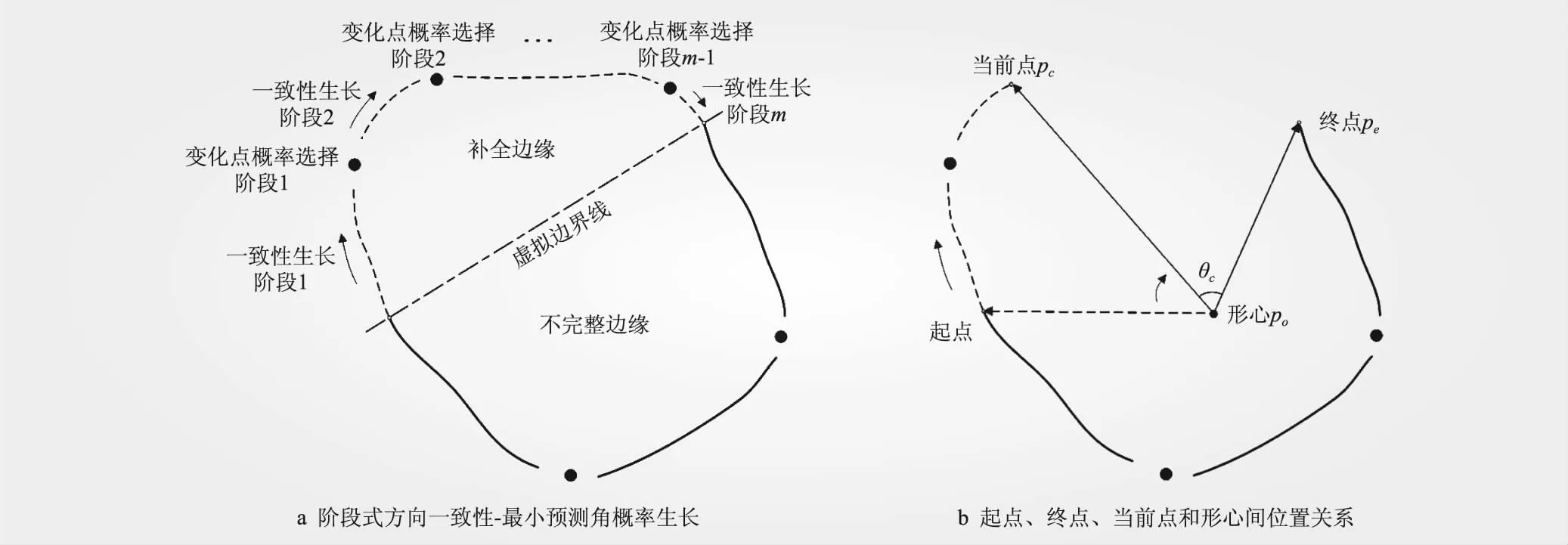
图3 多阶段颗粒边缘预测方法

(1)

(2)

式中，i*为预测点位；αi为候选点方向一致角；αsta为方向一致角标准值；pi(θmin)为最小角度-点位选择概率函数。

在阶段式颗粒边缘预测进程中，如图3b所示，根据当前点pc-初始形心点po-终点pe夹角θc与2π比值，提出补全参数ratio用于指示颗粒形态完整性。当颗粒边缘缺失程度较高时，ratio接近于1；当颗粒边缘逐步补全时，ratio逐渐减小至0。公式为

(3)

2 预测精度分析

颗粒边缘预测试验以机制白石子为研究对象，试验过程包括样本制备、形态预测，同时，从整体形态和级配准确率等方面分析预测结果。

2.1 样本制备

共采集100个满足一定级配的颗粒作为分析对象，如图4所示，根据颗粒的图像面积和等效粒径将颗粒分为5组，每组粒径范围分别为20～25、15～20、10～15、5～10、2～5 mm。

图4 颗粒分析样本

采用OV5647摄像头采集颗粒完整图像(像素2 000×2 000)，通过畸变校正[18]、灰度化、otsu阈值处理[19]、裁剪等操作提取颗粒对象。为便于后续分析，尝试调整原颗粒图像的尺寸，结果表明，在将颗粒从原像素调整至50×50时，面积误差平均值为0.87%，等效粒径误差从1.74%变为2.14%，仅增加0.4%。因此，在以颗粒级配为研究目标时，将图像进行大幅度尺寸缩小，是节省计算资源、减少数据计算量和计算时间的可行性办法。图5为颗粒图像调整大小和边缘提取示意，图6为图像尺寸调整前后级配曲线。

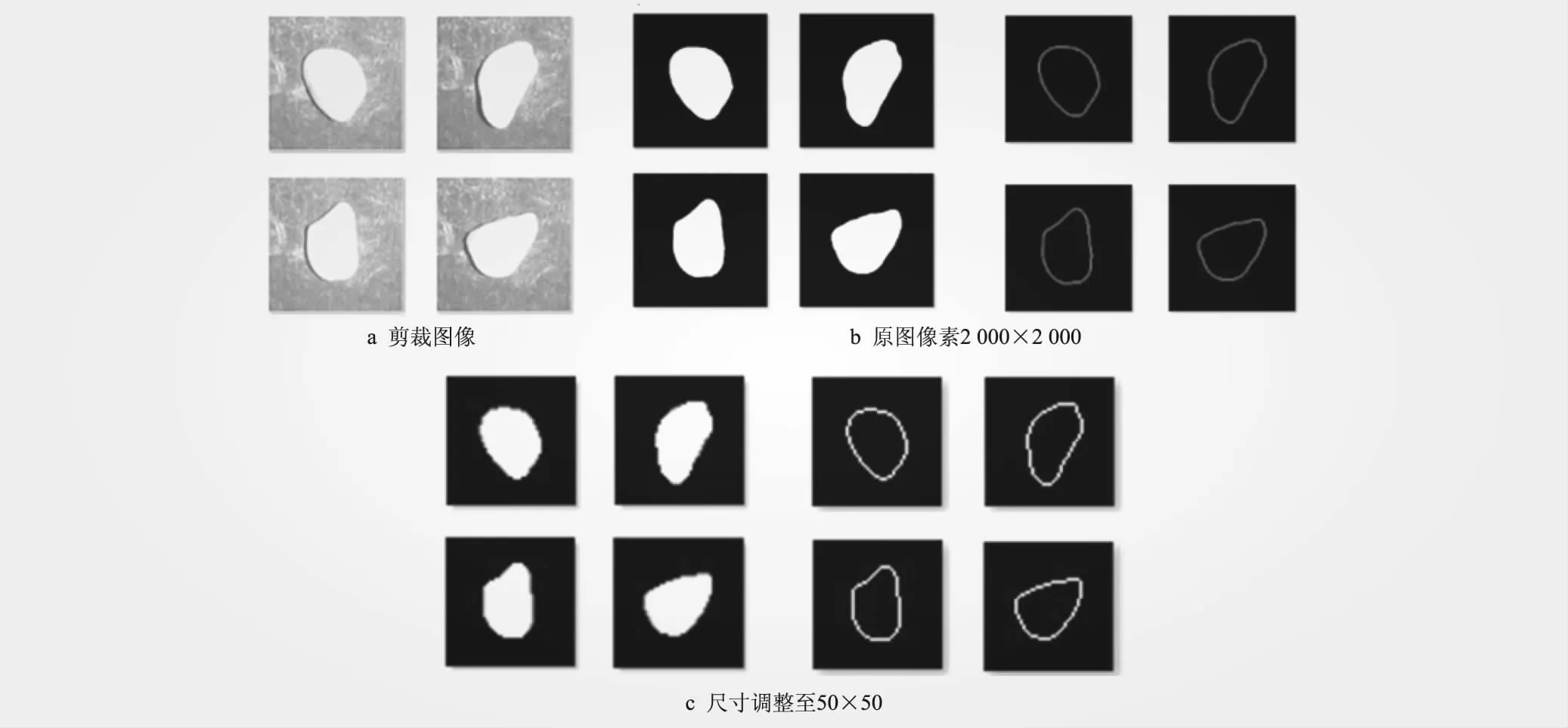
图5 图像尺寸调整和边缘提取

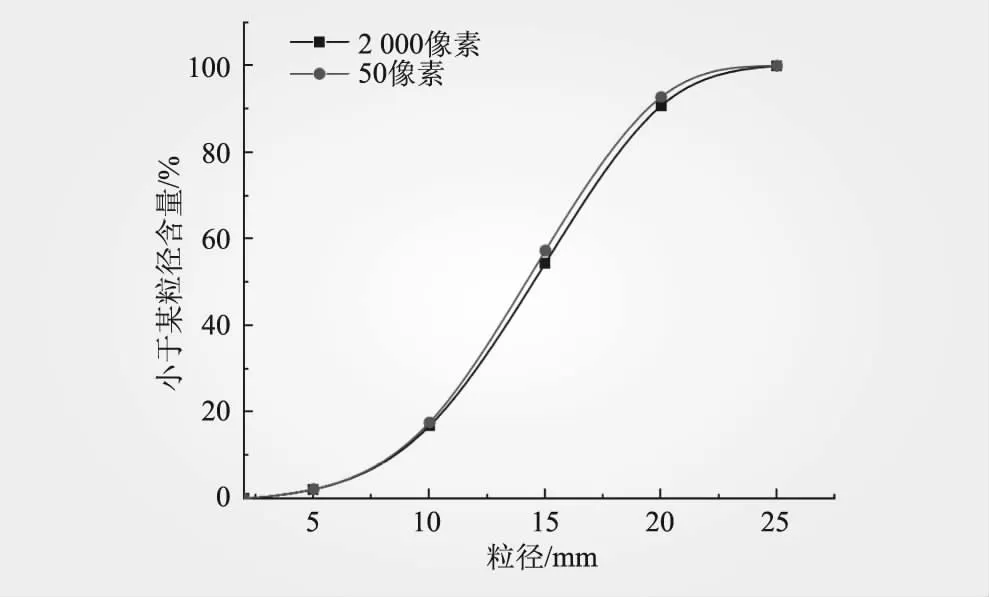
图6 图像尺寸调整前后级配曲线对比

基于颗粒之间不同的遮挡程度，按颗粒面积缺失比例制备4组缺失程度不同的颗粒边缘(每组100个)，保留部分分别为90%～95%、80%～90%、70%～80%、60%～70%，如图7所示，切割位置随机选择，模拟颗粒和颗粒之间的遮挡状态。

图7 不完整边缘

2.2 样本形态预测

自行编制颗粒边缘形态预测分析程序，统计颗粒真实边缘点的数据信息，包括最小预测角θmin、真实预测角、真实点位选择等，共计9 003组颗粒边缘信息，用于分析多阶段颗粒边缘预测方法的参数取值。

2.2.1 最小预测角-主点位概率函数

分析最小预测角θmin与点位选择之间的概率关系，如图8所示，1、2、3、7位点的总体选择概率为94.9%，称为主点位，而4、5、6位点为低概率选择点，称为次点位。当颗粒点之间的关系为主点位时，颗粒边缘走势较为平缓，而当选择次点位时，颗粒边缘会产生畸变。从变化规律分析，1位点和2位点的选择概率随最小预测角度变化很小，稳定在30%左右，3位点和7位点的选择概率以15°为分界对称变化。以补全普遍形状颗粒为目标时，假设所有预测点位均为主点位可使边缘无过多突变。

图8 最小预测角θmin与点位选择概率

以颗粒的边缘数据信息为基础建立最小预测角-主点位概率函数，在0～45°区间以2°为步长进行分组，统计各区间内θmin与真实点位选择信息，点位i选择公式为

(4)

式(4)中的部分点位选择概率参数值见表1。

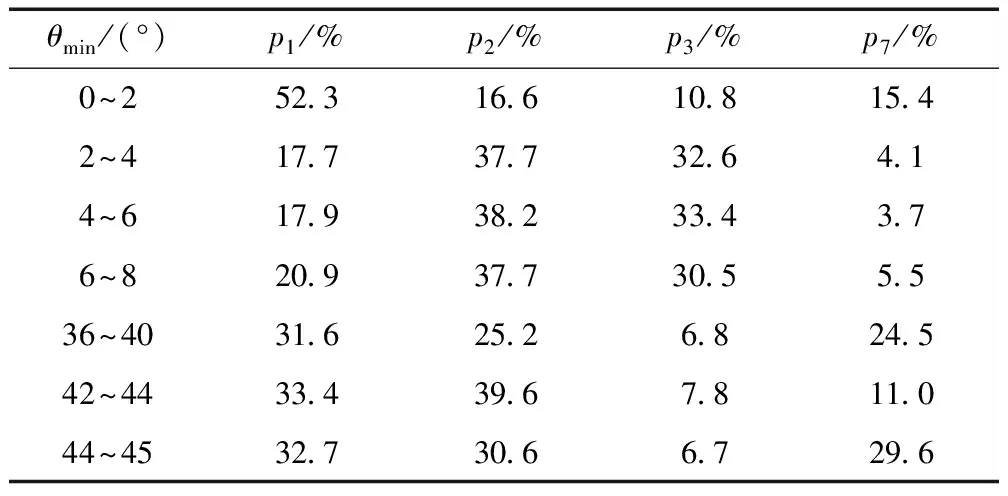
表1 部分点位选择概率参数

2.2.2 形态影响参数

以带有一定弧度的颗粒边界和方向一致性为预测目标时，方向一致角标准值αsta的取值影响预测边缘形态，采用试验分析论证，部分试验效果如图9所示，当αsta取值为3.2～3.8时，图像补全效果较好，符合颗粒方向一致性形态走势。

图9 方向一致性参数试验论证

在图像补全测试中，图像尺寸为50×50，方向一致性参数n取值5，αsta取值3.5，多阶段颗粒边缘预测方法中阶段ratio取值分别为0.27、0.25、0.19、0.17、0.12、0.11、0.07、0.06、0.04。

2.2.3 边缘补全结果

对面积缺失比例分别为10%、20%、30%、40%的颗粒进行补全试验，共计4组图像(每组100)，部分结果展示见图10。整体预测效果显示，多阶段颗粒边缘预测方法能够将缺失部分边缘的颗粒补全至完整状态，补全结果符合颗粒基本形状。

图10 颗粒预测效果展示

2.3 补全结果分析

级配分析中的基本信息为质量和等效粒径，在图像分析中简化为颗粒面积和最小外接圆直径。对比各组颗粒补全前后的颗粒面积和等效粒径，补全前颗粒的面积误差随缺失情况增加而增加，且误差数值与边缘缺失状态一致，如图11a所示；补全前颗粒的粒径误差相对面积误差来说数值较小，如图11b所示，这是因为颗粒在边缘不完整情况下，对于等效粒径计算的影响并不是线性增加的，但总体误差仍然呈上升趋势。由图11可知，进行补全后的面积和等效粒径误差均大幅度降低。

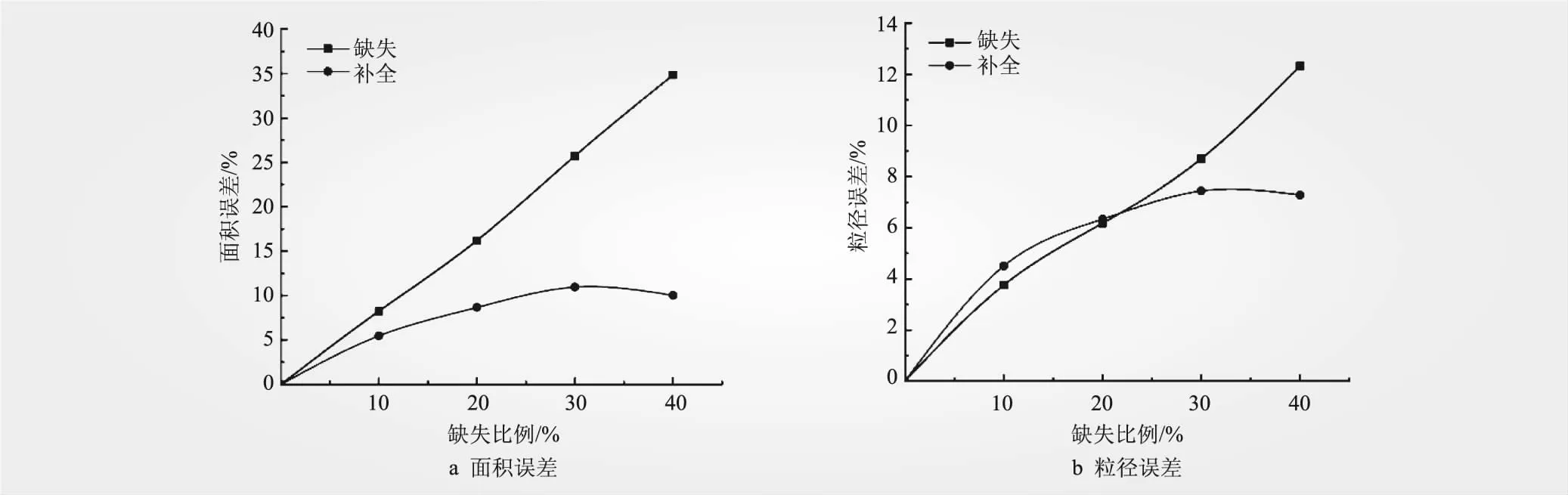
图11 颗粒边缘补全前后面积和等效粒径误差对比

进一步分析颗粒在边缘完整、缺失和补全3种状态下的级配曲线，如图12所示，进行形态补全后，颗粒级配曲线误差大幅度降低，根据式(5)计算级配准确率P[20]，即

图12 颗粒级配对比

(5)

式中，k为级配中粒径分级数量；Tk为原图颗粒第k级占比；Fk为补全颗粒第k级占比。

级配准确率结果如图13所示，级配准确率P并未随颗粒图像缺失程度增加而降低，补全后的级配准确率平均值为95.62%，说明多阶段颗粒边缘预测方法在级配分析中应用的有效性。

图13 颗粒边缘补全前后级配准确率对比

从理论上分析，虽然能够确定被遮挡颗粒的真实形态，但当颗粒处于被遮挡状态时，判断颗粒整体形态这个问题本身具有很大的不确定性，真实颗粒形状并不是规则图形，而是多样性的，预测被遮挡颗粒的边缘形态问题本身不具备绝对正确的结果，作为试验的对象仅为真实可能性中的一种。由于以上不确定性因素存在，本文用于预测缺失点的边缘信息，仍保留原本的60%以上，至于缺失边缘过大，通过已有的颗粒形态也无法判断遮挡颗粒大致的形状，不具备深入研究讨论的价值。

3 结 语

本文提出了一种基于方向一致性和最小预测角度的多阶段颗粒边缘预测方法，并以某一类颗粒为例进行边缘形态预测，验证该方法具有可行性和有效性。测试结果表明，多阶段颗粒边缘预测方法能够有效地补全颗粒缺失的边缘，预测结果符合颗粒的基本形状，补全效率高，面积40%缺失的单颗粒边缘补全时间小于0.01s，在级配分析的应用中，补全后的颗粒级配准确率大于95%，补全颗粒大幅度降低级配曲线误差，说明预测结果与颗粒真实状态具有较高的匹配度。