海洋平台GNSS RTK监测数据的CVCEEMDAN-WT-SSA去噪算法

2023-09-05熊春宝张子健于丽娜

测绘通报 2023年4期

熊春宝,张子健,陈雯,于丽娜

(天津大学建筑工程学院,天津 300072)

海洋平台长期处于恶劣的海洋环境中,并受到风、海流潮汐、波浪等多种荷载交互作用[1-2],结构本身也时刻经受环境腐蚀作用,一旦发生事故,将会给自然环境、社会经济及人身安全带来巨大的危害。因此,为了评估与维护平台的正常运行,有必要对海洋平台结构进行动态变形监测。全球卫星导航系统(global navigation satellite system,GNSS)[3]因其采样率高、自动化程度高、四维监测、全天候监测等优点,已被广泛应用于结构健康监测领域,如高层建筑、大跨桥梁、大坝等。在GNSS动态监测中绝大部分误差都可以通过一定的技术手段予以消除,只有多路径误差与随机噪声难以去除,需要借助额外的滤波算法进行去噪处理。具有自适应白噪声的完整集成经验模态分解[4-6](complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)算法是目前应用比较广泛的一种滤波方法,该算法在重构精度与去噪效果方面均优于经验模态分解[7](empirical mode decomposition,EMD)、集成经验模态分解[8](ensemble empirical mode decomposition,EEMD),其主要原理是将监测数据分解为一系列本征模态函数(intrinsic mode function,IMF)分量,识别并保留有效信号分量,舍弃或再处理噪声信号分量,重构形成最终去噪信号。因此,噪声和有效信号IMF分量的界定是影响去噪效果好坏的重要因素。文献[9—10]提出利用相关系数与归一化自相关函数实现噪声IMF分量的选取,但相关系数法太绝对且没有统一标准,自相关归一化函数图像也难以准确识别信噪分量。

交叉证认方法[11-12]对数据本身进行处理,可自适应地选择最优的平滑因子对数据作平滑处理,已经在信号处理领域有了一定的应用。本文利用交叉证认改进CEEMDAN(cross-validation improvement of CEEMDAN, CVCEEMDAN)算法,自适应地确定噪声与有效信号IMF分量,利用小波阈值(wavelet threshold,WT)去噪[13]和奇异谱分解(singular spectrum analysis,SSA)[14-15]分别对噪声及有效信号分量作去噪处理(记为CVCEEMDAN-WT-SSA去噪算法);并以噪声样本熵[16]为评判标准,通过与单一的EMD、EEMD算法及文献[9]算法进行对比,以验证本文算法的准确性与去噪效果。

1 CVCEEMDAN-WT-SSA去噪算法

CVCEEMDAN-WT-SSA去噪算法流程如图1所示。主要步骤如下:首先,利用CEEMDAN算法将原始信号数据分解为一系列IMF分量;其次,通过交叉证认方法识别出噪声IMF分量及有效信号IMF分量;然后,分别对噪声IMF分量及有效信号IMF分量使用WT和SSA进行去噪处理;最后,将两部分降噪结果重构获得最终真实变形监测信号。

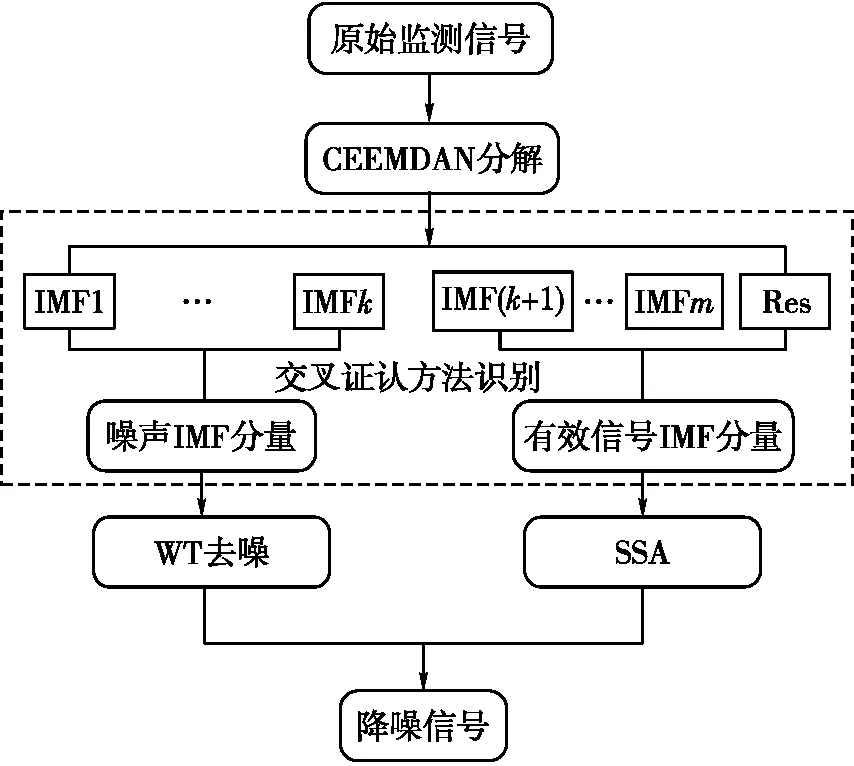
图1 CVCEEMDAN-WT-SSA去噪算法

1.1 基于交叉证认的CEEMDAN算法

交叉证认方法将原始数据划分为两个样本,通过数据内部间的相互验证,自适应地实现有效信号分量和噪声分量的分离[2]。具体算法如下:

(1) 将原始信号数据(ti,yi),i=1,2,…,N,分为奇数样本与偶数样本;选取奇数样本作为滤波样本,对偶数样本进行随机取样,组成证认样本。

(2) 对滤波样本进行CEEMDAN分解,并依次计算k～m(k=1,2,…,m)间IMF分量及残余分量之和;利用三次样条插值得到证认样本的滤波值f′(t2,i)。计算各证认样本对滤波值的方差为

(1)

式中,Pj表示对偶数样本的某一次随机取样;C表示方差值;k表示IMF序列数;n表示证认样本数。

(3) 计算W个证认样本方差的平均值为

(2)

(4) 选择最小平均值及其所对应的k值,则有效信号分量选择第k+1～m的IMF分量及残余分量Res。

1.2 奇异谱分析法

奇异谱分析法通过嵌入维度L将原始数据yi变换为Hankel轨迹矩阵X;对轨迹矩阵X进行奇异值分解X=USVT。其中,U、V均为正交矩阵,由奇异值对应的特征向量组成;对角阵S=diag(λ1,λ2,…,λL)代表X的奇异值。求解各奇异值的贡献率为

(3)

式中,δi代表对应分量所占的能量。由于有效信号IMF分量中的残存噪声所占能量远小于有效信号,选取累计贡献率超过0.99的前n项奇异值及对应的特征向量进行重构,完成降噪处理。

1.3 去噪效果评价

引入样本熵(sample entropy,SE)作为评价去噪效果的标准,熵是反映事物无序状态的一个物理量,无序程度越高,样本熵值越大。在信号处理过程中,去噪前后信号的差值即为所去除的噪声。噪声的样本熵会随着去噪效果的提升逐渐增大,如果去噪不充分或过度去噪导致噪声中含有一部分有效信号,则噪声的样本熵较小。

2 埕岛中心一号生活平台监测试验

2.1 工程概况

胜利油田埕岛中心一号生活平台如图2所示。该平台位于山东东营某海域,平台距离岸边约为8 km,1995年投产,主要功能为管理海上自动化监控、本平台职工食宿、办公及生活污水处理等,是一座四腿式导管架结构平台,总计3层,由基础部分和上部组块与生产平台、消防平台、动力平台、火炬平台连接的栈桥组成。

图2 胜利油田埕岛中心一号生活平台

2.2 GNSS-RTK监测试验

本次试验时间为2021年9月,试验监测仪器为4台海星达H32全能型双频接收机,其中1台作为基准站,其余仪器安装在监测点上。该仪器能同时接收来自GPS、GLONASS、BDS三系统的卫星信号,其仪器水平方向精度为10 mm+1×10-6D,高程方向精度为20 mm+1×10-6D,D为被测点间距离;采样频率设置为10 Hz,连续监测24 h,期间风力4～5级,短时达到7级以上。监测点设置在生活平台顶层甲板的3个角落,将RTK基准站设在陆上岸边。

3 试验数据的处理与分析

图3 原始信号CEEMDAN分解

图4 证认样本的方差均值随k值的变化趋势

采用文献[9]选取噪声IMF分量的方法,求解各IMF分量与原始数据的相关系数R,设定R=0.3作为判断噪声IMF分量与有效信号IMF分量的阈值,计算结果如图5所示;各IMF分量的自相关归一化函数图像,如图6所示。观察得出以下结论:IMF1—IMF5为噪声IMF分量,IMF6—Res为有效信号IMF分量。该结论与交叉证认方法所得结论不同。为验证本文算法的准确性,对文献[9]算法所得噪声IMF分量及有效信号IMF分量同样进行WT与SSA降噪处理(记为ACCEEMDAN-WT-SSA算法),通过对比噪声样本熵对两种算法的去噪效果进行评价。

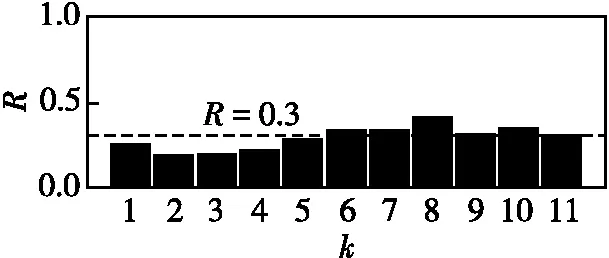
图5 各IMF分量对应的相关系数

图6 各IMF分量的归一化自相关函数图像

原始信号与本文算法的去噪效果如图7所示。可以看出,原始信号中存在大量的毛刺现象,说明原始监测数据包含大量噪声,严重影响对真实结构位移的判断;而经本文算法去噪后,信号中未出现明显的毛刺现象,有效去除了试验监测中存在的多路径误差与随机噪声。此外单独使用EMD、EEMD、CEEMDAN算法对原始数据进行去噪处理,计算上述所有算法的噪声样本熵(见表1),可知本文算法的噪声样本熵值大于ACCEEMDAN-WT-SSA算法所得样本熵,且明显大于单独使用EMD、EEMD、CEEMDAN去噪算法的结果,表明本文算法的去噪效果优于其他去噪算法。